Сапожников А.А. Решение самостоятельных и контрольных работ по алгебре и началам анализа за 11 класс
Подождите немного. Документ загружается.

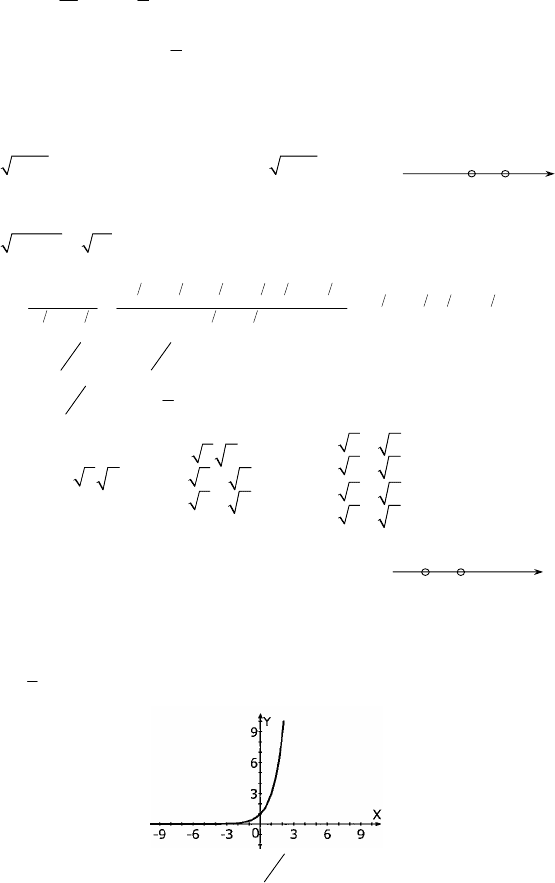
161
3. а)
4
1
16
x =
;
1
2
x =±
; б) 2x
2
– 3x + 2 = 4x
2
– 8x + 4; 2x
2
– 5x + 2 = 0;
(
x – 2)(x –1 ) = 0, т.к.
1
220
2
⋅
−<
. Ответ: x = 2.
4.
2
2
272
( ) 169
()25
xy
xy
xy
=
⎧
⎪
+=
⎨
⎪
−=
⎩
;
{
13
5
xy
xy
+
=
−
=
; x
1
=
±
9; x
2
=
±
4; y
1
=
±
4; y
2
=
±
9.
5.
20xx+−>. Решим уравнение 20xx
+
−=;
x + 2 = x
2
; (x – 2)(x + 1) = 0; x ∈ [–2; 2).
Вариант 4
1.
66
75 11 64 2−= =.
2. Применим формулу для суммы кубов:
13 13 23 13 13 23
23 13 13 23
13 13 13 13
()( )
()
ab a b a ab b
aabb
ab ab
++−+
==−+
++
.
3. а)
6
1
64
x = ;
1
2
x =± ; б) 2x
2
+ 5x + 4 = 4x
2
+ 8x + 4; 2x
2
+ 3x = 0;
x = 0, x =
3
2
−
т.к.
3
220
2
⋅− + < . Ответ: x = 0.
4.
2
13
215
()25
xy
xy xy
xy
+=
⎧
⎪
+
+=
⎨
⎪
−=
⎩
;
2
2
212
()25
()1
xy
xy
xy
⎧
=
⎪
+=
⎨
⎪
−=
⎩
;
5
4
5
1
xy
xy
xy
xy
⎡
⎧
+
=
⎢
⎨
−
=
⎩
⎢
⎧
⎢
+
=
⎨
⎢
−
=−
⎢
⎩
⎣
;
{
{
9
4
4
9.
x
y
x
y
⎡
=
⎢
=
⎢
=
⎢
=
⎣
Ответ: (4, 9) и (9, 4).
5. 2 –
x > x
2
; x
2
+ x – 2 > 0; (x + 2)(x – 1) = 0;
x ∈ (–∞; 1).
Контрольная работа № 3
Вариант 1
1. От
1
3
до 27.
2. а) 2
x
= 2
2
⋅ 2
6
= 2
8
; x = 8; б)
(
)
3
21 22
8
x
+=; 2
x
= 16 = 2
4
; x = 4.
3.
2
45
3 243 3
x −
≤=; x
2
– 4 ≤ 5; x
2
– 9 ≤ 0; x ∈ [–3; 3].
x
[
–
22
+
–
–
1
+
]
–
22
+
–
1
+
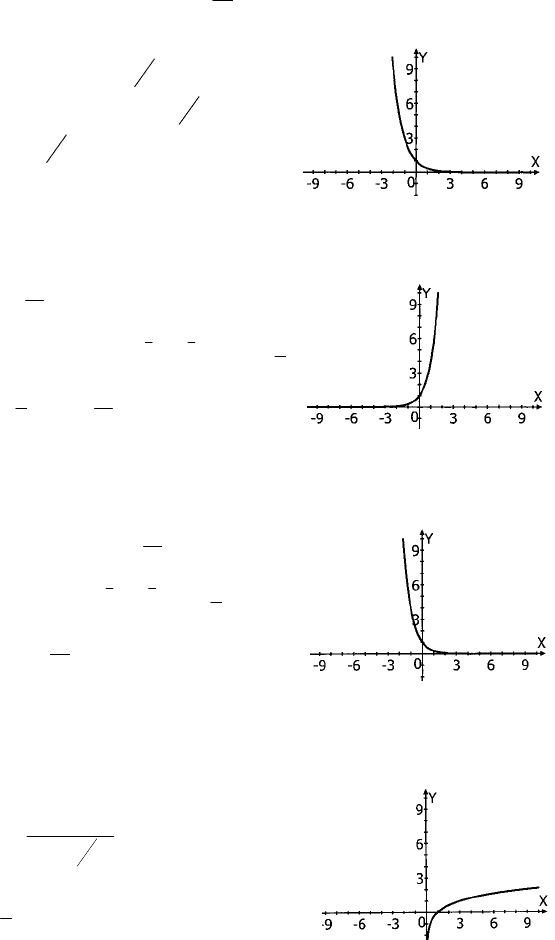
162
4. |sin
x – 1| = 2; sinx = –1;
3
2
2
x
n
π
=
+π
; n ∈ Z.
Вариант 2
1. Убывает от 3 до
1
27
.
2. а) 3
2x
= 3
4
⋅ 3
3
= 3
7
; x =
7
2
=3,5;
б)
1
3(1 ) 57
9
x
+=; 3
x
= 3
3
; x = 3.
3.
2
1
28
x −
≥ ; x
2
– 1 ≥ 3; x
2
≥ 4,
x ∈ (–∞; –2] ∪ [2; +∞).
4. |cos
x –2| = 3; cosx = –1; 2
x
n
=
π+ π .
Вариант 3
1. От
1
16
до 16.
2. а) 5
3x
= 5
–1
⋅
1
2
5
−
=
3
2
5
−
; 3x =
3
2
−
;
x =
1
2
−
; б)
13
452
16
x
⎛⎞
=
⎜⎟
⎝⎠
; 4
x
= 4
3
; x = 3.
3.
2
22 2
(0,3) (0,3)
xx−+
≤ ; x
2
– 2x + 2 ≤ 2; x(x–2) ≤ 0, x ∈ (–∞; 0] ∪ [2; +∞).
4. |
x – 1| = x – 1; x ≥ 1.
Вариант 4
1. Убывает от 16 до
1
16
.
2. а) 3
2x
= 3
–2
⋅
1
2
3
−
=
5
2
3
−
; x =
5
4
−
;
б)
7
51 90
25
x
⎛⎞
−=
⎜⎟
⎝⎠
; 5
x
= 5
2
⋅ 5 = 5
3
; x = 3.
3.
x
2
– 4x + 2 ≤ 2; x ∈ [0; 4].
4. 5
|x+1|
= 5
x+1
; x ≥ –1.
Контрольная работа № 4
Вариант 1
1. Возрастает от –1 до 3.
2. а)
2
2
2
log 3
2
1
log
2
xx−
=−
; x
2
– 3x – 4 = 0;
(
x – 4)(x + 1) = 0; x = 4, –1;
б)
22
1
log log 3
2
xx+=
; log
2
x = 2; x = 4.
163
3. log
4
(x + 1) < –0,5; x + 1 <
1
1
2
1
42
2
−
−
=
= ;
1
1
2
x
x
≥−
⎧
⎨
<−
⎩
⇒ x ∈ [–1; –
1
2
).
4.
{
4
27
xy
yx
=
−=
;
2
72
72 40
yx
xx
=+
⎧
⎨
+−=
⎩
;
(
)
1
(4) 0
2
72
xx
yx
⎧
⎪
+
−=
⎨
=+
⎪
⎩
;x =
1
2
; y = 8.
5.
2
log (3 )
0
x
x
−
≥
; x ∈ (0; 2].
Вариант 2
1. Убывает от 1 до –3.
2. а) x
2
+ 4x – 5 = 0; (x – 1)(x + 5) = 0;
x = 1, x = –5;
б)
33
1
log log 1
2
xx−+ =−
; log
3
x
(
)
1
2
−
=
= –1; log
3
x = 2; x = 9.
3. log
0,5
(x – 1) > –2; log
2
(x – 1) < 2;
0 <
x – 1 < 4; x ∈ (1; 5).
4.
{
3
38
xy
yx
=
−=
;
{
(8 3 ) 3
3
xx
xy
+=
=
; x =
1
3
; y = 9.
5.
0,5
log ( 3)
0
x
x
+
≥
;x ∈ [–2; 0).
Вариант 3
1. Убывает от 2 до –3.
2. а)
2
2
2
log ( 6 )
2
1
log
4
xx+
=−
; x
2
+ 6x – 16 = 0;
(
x – 2)(x + 8) = 0; x = 2, x = –8;
б)
22
853 1
log log
22 2
2
x
xx
=
−=−
⋅
2
3log 6x−=;
2
log 2x = ; 4x
=
;
3
2
log
2
x = 3; log
2
x = 2; x = 1.
3. lg
x(lgx – 1) > 0; lgx ∈ (–∞; 0) ∪ (1; +∞), x ∈ (0; 1) ∪ (10; +∞).
4.
{
4
15 4
xy
x
y
=
=+
;
{
4
(15 4 ) 4
xy
yy
=
+=
;
2
41540
4
yy
x
y
⎧
+
−=
⎪
⎨
=
⎪
⎩
; y =
1
4
; x = 16.
5.
0,4
log ( 2)
0
6
x
x
−
≤
−
;x ∈ (2; 3] ∪ (6; +∞).
Вариант 4
1. Возрастает от –1 до 2.
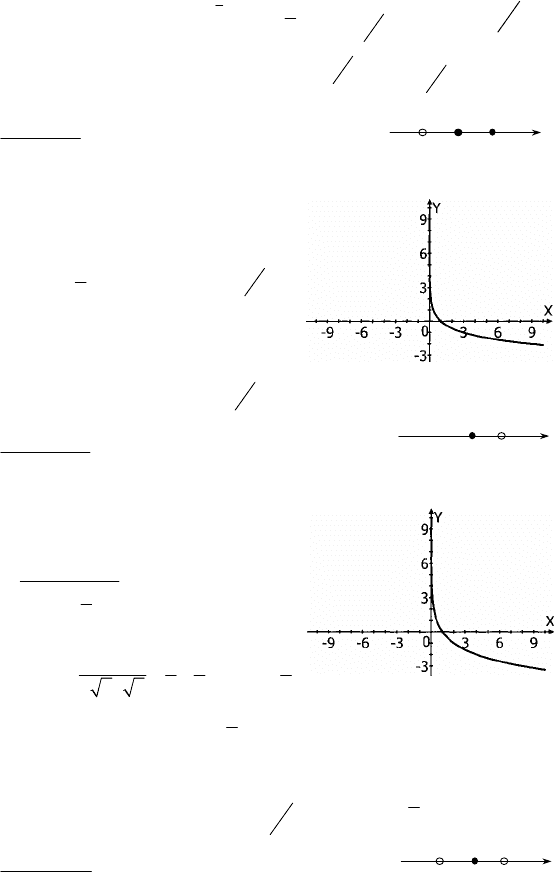
x
]
0
3
–
–
2
+
[
–
30
–
+
–
2
–
[
26
–
+
3
–

164
2. а)
1
3
log (x
2
+ 8x) = –2; x
2
+ 8x = 9; (x+9)(x–1)=0; x
1
=–9; x
2
=1;
б)
55
11
2log log 2
22
xx−++ =
;
51
22
−
log
5
x = 2; log
5
x = 1; x = 5.
3. lg
x(lgx + 1) < 0; lgx ∈ (–1; 0); x ∈
(
)
1
;1
10
.
4.
{
2
23
xy
xy
=
−=
;
{
2
(3 2 ) 2
xy
yy
=
+=
;
2
2
32 20
xy
yy
=
⎧
⎨
+
−=
⎩
; y =
1
2
; x = 4.
5.
3
log (8 )
0
4
x
x
−
≤
−
;x ∈ (4; 7].
Контрольная работа № 5
Вариант 1
1. а) f′(x) = e
x
(cosx – sinx); f(0) = 1; б) ϕ′(x) =
1
6
x
−
;
14
83
⎛⎞
′
ϕ
−=
⎜⎟
⎝⎠
.
2.
2
2
2
1
0
0
1
xx
Sedxe e===−
∫
; S
2
= y(x
2
–x
1
)= 1(2–0)=2; S=S
1
–S
2
=e
2
–1–2=
= e
2
–3 ≈ 4,4.
3.
f′(x) = 2lnx + 2; f′(x) = 0; lnx = –1; x = e
–1
; f убывает на (0; e
–1
]; возрас-
тает на [
e
–1
; +∞); x
min
= e
–1
.
4.
f′=4
t
ln4; ϕ′ = 2
t+1
ln2; 2
2t
> 2 ⋅ 2
t
ln 2
ln 4
=2 ⋅ 2
t
2
1
=2
t
; 2
2t
–2
t
> 0; 2
t
(2
t
–1) > 0,
2
t
–1 > 0; t > 0.
Вариант 2
1. а) f′(x) = e
x
(sinx + cosx); f(0) = 1; б) ϕ′(x) =
1
6
x
;
3
1
()
92
′
ϕ− =−
.
2.
S =
4
4
1
1
1
33ln
x
x
−=−
∫
= 3 – ln4
≈
1,61.
3.
f′(x) = e
x
+ xe
x
= e
x
(x+1); f′ = 0 при x = –1; убывает при x ∈ (–∞; –1);
возрастает при
x ∈ [–1; +∞); x
min
= –1.
4.
f′ = 2ln3 9
2t–1
; ϕ′ = 2ln3 3
t
; 2t – 2 < t; t < 2, t ∈ (–∞; 2).
Вариант 3
1. а) f′(x) = 2
x
ln2cosx – 2
x
sinx = 2
x
(ln2 ⋅ cosx – sinx); f′(0) = ln2;
]
48
+
+
7
–
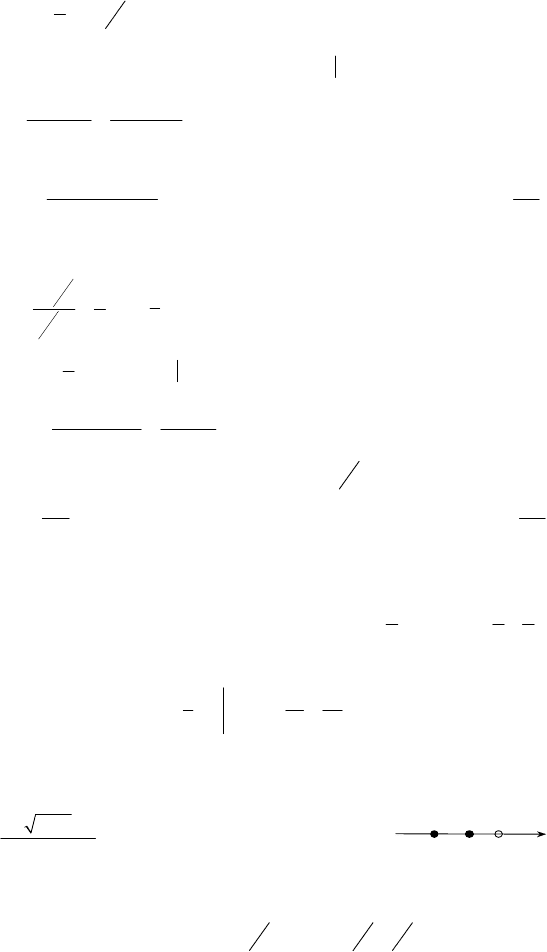
165
б)
ϕ′(x) =
6
x
;
1
()12
2
′
ϕ=
.
2.
S = –2 +
00
0
2
2
22
2()2 3
xx x
edx ed x e e
−− −
−
−−
=− − − =− − =− +
∫∫
= e
2
– 3
≈
4,4.
3.
f′ =
22
22ln 2(1ln)
x
x
xx
−−
=
; f = 0 при x = e; возрастает на (0; e]; убывает
на [
e; +∞); x
max
= e.
4.
f′(x) =
3 ln3 3 ln3
33
ln 3
xx
x
x
−
−
−
=−
; f′ = 0 при x = 0; тогда f
min
= f(0) =
2
ln 3
.
Вариант 4
1. а) f′ = 3
x
ln3sinx + 3
x
cosx = 3
x
(ln3 ⋅ sinx + cosx); f′(0) = 1;
б)
ϕ′ =
1
6
6
3
1
3
x
x
⋅
=
;
1
18
3
⎛⎞
′
ϕ=
⎜⎟
⎝⎠
.
2.
S = 4 –
3
3
1
1
2
42ln 4ln91,8dx x
x
=− =− ≈
∫
.
3.
f′(x) =
2
444(1)
xx
xx
ee x x
ee
−⋅ −
=
; f = 0 при x = 1; возрастает на (–∞; 1];
убывает на [1; +
∞); x = 1 — максимум, f(1)=
4
e
.
4.
f′(x)=
1
3
ln 2
x
(2
х
ln2 – 2
–x
ln2) = 2
x
–2
–x
; f′=0 при x=0; тогда f
min
=f(0) =
2
ln 3
.
Контрольная работа № 6
Вариант 1
1. sin2x + cos2x = 0; tg2x + 1 = 0; tg2x = –1; 2x =
4
n
π
−
+π
;
82
x
n
π
π
=− +
;
n ∈ Z.
2.
S = 16 –
2
2
23
2
0
11632
16 2 16
333
xdx x
−
⎛⎞
=− =−=
⎜⎟
⎝⎠
∫
.
3.
3
1
log ( ) 1
3224
xy
yx
+
−=
⎧
⎨
⋅=
⎩
;
13
3
32 24
xx
yx
++
−=
⎧
⎨
⋅
=
⎩
;
3
32 1
xx
yx
=
+
⎧
⎨
⋅
=
⎩
; x = 0; y = 3.
4.
5
0
(3)(3)
x
xx
+
≥
−+
; x ∈ [–5; –3] ∪ (3; +∞)
5.
f′(x) = e
x
+ cosx; f′(0) = 2; y = f′(x
0
)(x – x
0
) + f(x
0
); y = 2x + 1.
Вариант 2
1. sin2x – cos2x = 0; tg2x = 1; 2x =
4
n
π
+
π ;
82
x
n
ππ
=+ ; n ∈ Z.
[
–
5
3
+
–
–
3
+
166
2.
S
1
=
2
2
2
2
2
2
1888
26 663
x
dx x
−
−
==+=
∫
; S
2
= y(x
2
–x
1
)= 2(2–(–2))=8;
S = S
1
– S
2
=
816 1
85
33 3
−= =
.
3.
21
2
23 72
yy
xy
++
−=
⎧
⎨
⋅=
⎩
;
2
23 6
yy
x
y=+
⎧
⎨
⋅
=−
⎩
; y = 1; x = 3.
4.
6
0
(2 )(2 )
x
xx
+
≤
−+
; x ∈ [–6; –2) ∪ (2; +∞).
5.
f′ = e
x
– sinx; y = x + 2.
Вариант 3
1. sin
2
x + sinxcosx = 0; tg
2
x + tgx = 0; tgx = 0; tgx + 1 = 0; x =
nπ
;
4
x
k
π
=− +π
; n, k ∈ Z.
2.
S =
()
0
0
23
1
1
11 1211
(1 )
23 2326
xdx x x
−
−
− −=− −=−=
∫
.
3.
11
3
25 40
yy
xy
+−
−=
⎧
⎨
⋅=
⎩
;
3
2 5 100
yy
xy=+
⎧
⎨
⋅=
⎩
; y = 2; x = 5.
4.
f′ = e
x+1
– e; f′ = 0; x = 0; f(–1) = 1 + e; f(0) = e; f(1) = e
2
– e; f
max
= e
2
– e;
f
min
= e.
5. Т.к. 3
x
2
+ 4 ≥ 0 для всех x, то 2sinx + 1 > 0; sinx ≥
1
2
−
;
7
[2; 2]
66
x
nn
ππ
∈− + π + π .
Вариант 4
1. cos
2
x–sinxcosx=0; cosx = 0; sinx = cosx;
2
x
n
π
=
+π
;
4
x
n
π
=
+π
, n ∈ Z.
2.
S =
0
3
0
2
1
1
11111
(1) 1
23 2326
x
xdx x
−
−
⎛⎞
−+ −=− + −=−−=
⎜⎟
⎜⎟
⎝⎠
∫
.
3.
43
2
34 36
yy
xy
++
+=
⎧
⎨
⋅=
⎩
;
2
1
34
16 : 9
yy
xy+=
⎧
⎪
⎨
⋅=
⎪
⎩
; y = –2; x = 4.
4.
f′ = e
x+2
– e; f′ = 0; x = –1; f(–1) = 2e; f(–2) = 1 + 2e; f(0) = e
2
; f
min
= 2e;
f
max
= e
2
.
5. Т.к. –2
x
2
– 5 < 0 для всех x, то 2cosx + 1 ≥ 0; cosx ≥
1
2
−
;
22
[2;2]
33
xnn
ππ
∈− + π + π
.
x
[
–
6
2
–
2
167
ПРИМЕРНЫЕ ВАРИАНТЫ ЭКЗАМЕНАЦИОННЫХ РАБОТ
Вариант 1
1. 1) 5 – 5sinx = 2(1 – sin
2
x); 3 – 5sinx + 2sin
2
x = 0;
(sin
x – 1)
3
sin 0
2
x
⎛⎞
−=
⎜⎟
⎝⎠
; n ∈ Z,
2
2
x
n
π
=
+π
;
2) промежутку [
π; 5π] принадлежат
3
2
π
,
9
2
π
.
2. log
2
(1 – x) + log
2
(–5x – 2) = log
2
4 + log
2
3; (1 – x)(–5x – 2) = 12;
5
x
2
+ 2x – 5x – 2 = 12; 5x
2
– 3x – 14 = 0; (x – 2)
(
)
7
5
x +
= 0, т.к. 1 – 2 < 0.
Ответ:
7
5
x =−
.
3.
2
7
0
3
x
x
−
≤
+
; x ∈ (–3; 7− ] ∪ [ 7 ; +∞).
4. Найдем точки пересечения 5
x
2
— 5 = 0, x = ±1;
S = S
1
– S
2
=
1
3
111
22 2
111
1
(5 – 2 ) 3 (5 – 5 ) 5
3
x
xdx xdx xdx x
−−−
−
⎛⎞
−
==−=
⎜⎟
⎜⎟
⎝⎠
∫∫∫
=
11 102
51 1 10 6
33 33
⎛⎞
⎛⎞
−−−+ = − =
⎜⎟
⎜⎟
⎝⎠
⎝⎠
.
5.
2
90
sin 0
x
x
⎧
−
>
⎨
>
⎩
;
{
(3;3)
[2 ; 2 ]
x
x
nn
∈−
∈π π+π
; n ∈ Z; x ∈ [0; 3).
6.
22 22 2
31 2( 3) 3 6 2
2 3 3 4 12 12 4
x
xxxxxxxxx
y
−−+−−
⎛⎞
′
=+= ==
⎜⎟
⎝⎠
; y′ = 0 при
x=0 и x=2, на x∈(2; 6], f(x) — возрастает, следовательно: f
max
= f(6)=10.
Вариант 2
1. (sinx – cosx)
2
= 1+sinx; sin
2
x – sin
2
x + cos
2
x = 1 + sinx; sin2x + sinx = 0;
sin
x(cosx + 1) = 0; x = πn;
2
2
3
x
k
π
=
±+π
, n, k ∈ Z.
2.
y′ =
2
cos
32 2 2
x
x
−ππ
⎛⎞
−
⎜⎟
−
⎝⎠
; y′(1) = –2; уравнение касательной имеет вид:
y = y′(x
0
)(x – x
0
) + y(x
0
); y = –2(x – 1) + (–1) = –2x + 1.
3.
2
5
0
3
x
x
−
≥
−
; x ∈ (–∞;
5−
] ∪ [
5
; 3)
4.
S =
1
1
23
1
1
222482
(2 2 ) 2 2 2 4 2
333333
xdx x x
−
−
⎛⎞
−=−=−+−=−==
⎜⎟
⎝⎠
∫
.
[
–
3
–
+
7−
–
7
3
5−
5
168
5.
6.
23
32
xx
y
+
⎛⎞
′
=−
⎜⎟
⎝⎠
;
22
233 (3)
32 23 2 2
xx x xx x
y
⎛⎞
++
⎛⎞
′
=
−−⋅=−+=
⎜⎟
⎜⎟
⎜⎟
⎝⎠
⎝⎠
=
2
36
10
x
x
⎛⎞
+
−
⎜⎟
⎜⎟
⎝⎠
; y′ = 0 при x = 0 и x =
6
5
−
; y
min
= y(3) = 0.
Вариант 3
1. 3sin2x – 2cos2x=2; sinx cosx – 2(2cos
2
x – 1) = 2; –4cos
2
x + 6sinx cosx = 0;
cos
x(6sinx – 4cosx) = 0; cosx = 0; 6sinx – 4cosx = 0;
2
x
n
π
=
+π
; tgx =
2
3
;
n ∈ Z; x = arctg
2
3
+ πn, n ∈ Z.
2. 4(2 +
3
)
–1
+ (2 +
3
)
n
= 15; 4 + (2 +
3
)
3
= 15(2 +
3
);
4 + 8 + 3
⋅ 4 3+ 3 ⋅ 3 ⋅ 2 + 3 3 = 30 + 15 3; 15 3 + 30 = 30 + 15 3.
Да, является.
3.
22
1
4
2
1
93
81
xy
xy
⎧
−=
⎪
⎨
⎪
⋅=
⎩
;
281
1
4
2
1
93
81
xx
yx
−
⎧
=−
⎪
⎨
⎪
⋅=
⎩
;
12
1
4
2
1
3
27
x
yx
⎧
=
−
⎪
⎨
⎪
=
⎩
; 12x = –3; x =
1
4
−
; y =
3
2
−
.
4. (
x + 2)
2
90x−≤; x ∈ [–3; –2] ∪ [3].
5. Найдем точки пересечения: –0,5
x
2
+x+1,5=0,5x+0,5; 0,5x
2
–0,5x–1 = 0;
x
2
– x – 2 = 0; (x + 1)(x – 2) = 0.
S =
22
2
11
( 0,5 1,5) (0,5 0,5)
x
xdx x dx
−−
−++ − + =
∫∫
2
2
1
(0,5 0,5 1)
x
xdx
−
−
++=
∫
2
32
1
81161
12 1 4
64 6 64 44
xx
x
−
⎛⎞
⎛⎞
=− + + =− ++ − + − = − − =
⎜⎟
⎜⎟
⎜⎟
⎝⎠
⎝⎠
79 1
42
44 4
−==
.
6. Пусть одно
x, тогда второе 2x, 3–е y. S=x
2
+4x
2
+y; 3x+y=28; y=28–3x;
S = 5x
2
+ (28 – 3x)
2
; S′ = 10x + 2(28 – 3x) ⋅ (–3) = 10x + (56 – 6x) ⋅ (–3) =
= 28
x – 56 ⋅ 3 = 0; x = 6, тогда y = 10.
Ответ: 6, 12, 10.
[
–
33
+
–
–
2
]
169
Вариант 4
1. 2cos
2
x = 1 – sinx; 2(1 – sin
2
x) = 1 – sinx; 2 – 2sin
2
x = 1 – sinx;
2sin
2
x – sinx – 1 = 0; (sinx – 1)
1
sin 0
2
x
⎛⎞
+
=
⎜⎟
⎝⎠
;
2
x
n
π
=
+π
;
1
(1)
6
k
x
k
+
π
=− +π, n, k ∈ Z.
2.
111
22
222
(2)(2) 1
16 16 2
aaa
a
+−−
== .
3.
3
3210
2log2
y
x
yx
⎧
+=
⎨
−=
⎩
;
312 10
318
y
y
x
x
⎧
−
=
⎨
=
⎩
;
3
20 10
log 18
x
yx
=
⎧
⎨
=
⎩
;
1
2
2
x
y
⎧
⎪
=
⎨
⎪
=
⎩
.
4.
2
lg(2 0,5)
0
lg( 1)
x
x
+
≤
+
; lg(x
2
+ 1) > 0 при x ≠ 0;
1
lg 2 0
2
x
⎛⎞
+
≤
⎜⎟
⎝⎠
;
1
20
2
x
+
≥
;
1
2
2
x ≤
; x ≥
1
4
−
; x ≤
1
4
;
11
;0 0;
44
x
⎡
⎞⎛ ⎤
∈− ∪
⎟⎜
⎢
⎥
⎣
⎠⎝ ⎦
.
5.
S =
2
22 2
2
22
11 1
1
222
22 41(3)2xdx dx x dx x
x
xx
⎛⎞⎛⎞
−=−=+=+−=
⎜⎟⎜⎟
⎝⎠⎝⎠
∫∫ ∫
.
6. Очевидно (из соображений симметрии), что стороны прямоуголь-
ника симметричны относительно
OY, тогда:
S = 2x ⋅
23
12
48
33
x
xx
⎛⎞
−+=−
⎜⎟
⎝⎠
; S′ = 8 – 2x
2
; S′ = 0; 8 = 2x
2
; x = ±2, т.е.
прямоугольник с вершинами (2, 0), (—2, 0), (–2,
f(–2)), (2, f(2)).
Вариант 5
1. sin
2
x – cos
2
x =
3
2
; –cos2x =
3
2
;
5
22
6
x
n
π
=
±+π
, n ∈ Z;
5
12
x
n
π
=± +π
, n ∈ Z.
2.
x + 2 =
2
261xx++; x
2
+ 4x + 4 =
=2
x
2
+ 6x + 1; x
2
+ 2x – 3 = 0;
(
x + 3)(x – 1) = 0, т.к. при x=–3 2x
2
+ 6x + 1 < 0.
Ответ:
x = 1.
3.
y = 2x
3
–1,5x
4
; y′ = 6x
2
– 6x
3
= 6(1 – x)x
2
;
y′ = 0 при x = 0, x = 1; функция возрастает на
(–
∞; 1); убывает на (1; +∞); x
max
= 1, y
max
= 0,5.

170
4.
()
2
0,3
1
lg
24
0
log 1
x
x
⎛⎞
+
⎜⎟
⎝⎠
≥
+
, x ≠ 0; lg
x
[
–
22
+
–
–
1
+
;
1
01
24
x
≤
+≤
;
13
424
x
−
<≤
;
13
22
x−<≤
;
13
;0 0;
22
x
⎛⎞⎛⎤
∈− ∪
⎜⎟⎜
⎥
⎝⎠⎝⎦
.
5.
y′ = 2x + 6; y′ = 0 при x
0
= –3, тогда уравнение касательной y = 1;
S =
3
0
6
22
3
3
( 6 10) 3 3 10 3 9
3
x
xx dx x x
−
−
⎛⎞
++ −= + + −=
⎜⎟
⎜⎟
⎝⎠
∫
.
6. Пусть одна сторона
x, вторая y: 2x+y=24; 2x=24–y; 2x⋅y=S; (24–y)y=S;
24
y – y
2
= S; S′ = 24 – 2y = 0; y = 12; x = 6.
Вариант 6
1. log
7
x(x + 6) = 1; x
2
+ 6x – 7 = 0; (x + 7)(x – 1) = 0, т.к. x = –2 < 0, то
при
x = 1.
2. (
x – 5)
2
9x −≥ 0; x ≥ 5 и x = 3
±
.
3.
()
()
2
1
71
1
37
42
−
+
−− =−
;
()()
2
71 3 7
273
2
+−
−
=−;
(
)
(
)
2
47137276−+ −= −;
(
)
(
)
4 8 27 3 7 27 6
−
+−=−
;
4 – 24 –
67+ 87– 14 = 27– 6; 27– 6 = 27– 6 — да, является.
4.
2
2
3
3
0
0
19
3cos 3sin 3 1
6622
xdx x
π
π
ππ
⎛⎞ ⎛⎞⎛⎞
−= −=+=
⎜⎟ ⎜⎟⎜⎟
⎝⎠ ⎝⎠⎝⎠
∫
.
5.
2
3
3
x
y
′
=−
; y′ = 0; x = ±3; возрастает на [–3; 3]; убывает на (–∞; –3] ∪
[3; +
∞); x
min
= –3; x
max
= 3.
6. Пусть
x и y — стороны.
S = xy = 5,76 Га
2
=57600 м
2
; 2x + 2y = L
— длина изгороди;
2
2 57600 м
2
x
L
x
⋅
+
= ;
2
2
2 57600 м
20
L
x
⋅
′
=− =
; x
2
= 5,76;
x = 2,4.
Это квадрат со стороной 2,4.
[
–
3
35
]
