Сапожников А.А. Решение самостоятельных и контрольных работ по алгебре и началам анализа за 11 класс
Подождите немного. Документ загружается.

141
2. а) 2tg2
x ≤ 3tgx;
2
4tg
4tg
x
x
−
– 3tgx ≤ 0;
2
2
tg (1 tg )
0
1tg
xx
x
+
≤
−
; tg
2
x + 1 > 0 для
всех
x, тогда неравенство имеет вид:
2
tg
0
1tg
x
x
≤
−
; tgx = y;
0
)1)(1(
≤
−+ yy
y
. Воспользуемся методом
интервалов: y ∈ (–1; 0] ∪ (1; +∞); y = tgx;
x ∈
;;
442
nn n n
πππ
⎛⎤⎛ ⎞
−+π π∪ +π +π
⎜⎜⎟
⎥
⎝⎦⎝ ⎠
, n ∈ Z.
б)
43
sin cos( )
32
x
π
⎛⎞
π≥
⎜⎟
⎝⎠
;
42
cos 2 ; 2
333
nnn
πππ
⎡
⎤
π
∈+π +π
⎢
⎥
⎣
⎦
, n ∈ Z,
13 13
cos ;
42 22
x
nn
⎡⎤
π∈ + +
⎢⎥
⎣⎦
, n, r, m ∈ Z;
5
[2; 2]
33
11
[arccos( ) 2 ; arccos 2 ]
44
xnn
x
nn
ππ
⎧
π∈ +π +π
⎪
⎨
⎪
π∈ − + π + π
⎩
и πx = π + 2πk; x = 1 + 2πk, то-
гда x ∈
11
arccos arccos
44
11
[2;2][2;2]
33
nn n n
−+−+∪+ +
ππ
∪ {1 + 2k}.
ПС-8
1. а) –6sin
2
x + 5sinx – 1 ≥ 0; sinx = t; –6t
2
+ 5t – 1 ≥ 0; 6t
2
– 5t + 1 ≤ 0;
(
)
(
)
11
0
32
tt−−≤
;
11
[;]
32
t
∈ ,
5
11
arcsin 2 ; 2 2 ; arcsin 2
36 6 3
x
nn n n
ππ
⎡⎤⎡ ⎤
∈+π+π∪+π−+π+π
⎣⎦⎣ ⎦
;
б) y = log
2
log
4
log
8
x;
8
48
0
log 0
log log 0
x
x
x
⎧
>
⎪
>
⎨
⎪
>
⎩
;
8
0
1
log 1
x
x
x
⎧
>
⎪
>
⎨
>
⎪
⎩
; x > 8;
в) y = log
sinx
cos2x;
sin 0
sin 1
cos 2 0
x
x
x
>
⎧
⎪
≠
⎨
>
⎪
⎩
;
()
()
2; 2
2
2
;
44
xn n
xm
x
kk
⎧
∈ππ+π
⎪
⎪
π
≠+π
⎨
⎪
ππ
∈
−+π +π
⎪
⎩
; n, k, m ∈ Z,
3
2; 2 2; 2
44
x
nn nn
ππ
⎛⎞⎛ ⎞
∈π +π∪ +ππ+π
⎜⎟⎜ ⎟
⎝⎠⎝ ⎠
.
2. а) f(–x) = cos
2
x – tgx
4
– f(x) — четная;
б) f(–x) =
(
)
2
ln 1xx−+ −
— ни четная, ни нечетная;
в) f(–x) = –tg ctgx+ ctg tgx — нечетная.
–
11
y
+
–
0
–
+
142
3. т.к. функция нечетная, f(0) = 0 и она возрастает на (–∞; +∞), тогда
|f(x)| ≥ f(3); x ∈ (–∞; –3] ∪ [3; +∞).
ПС-9
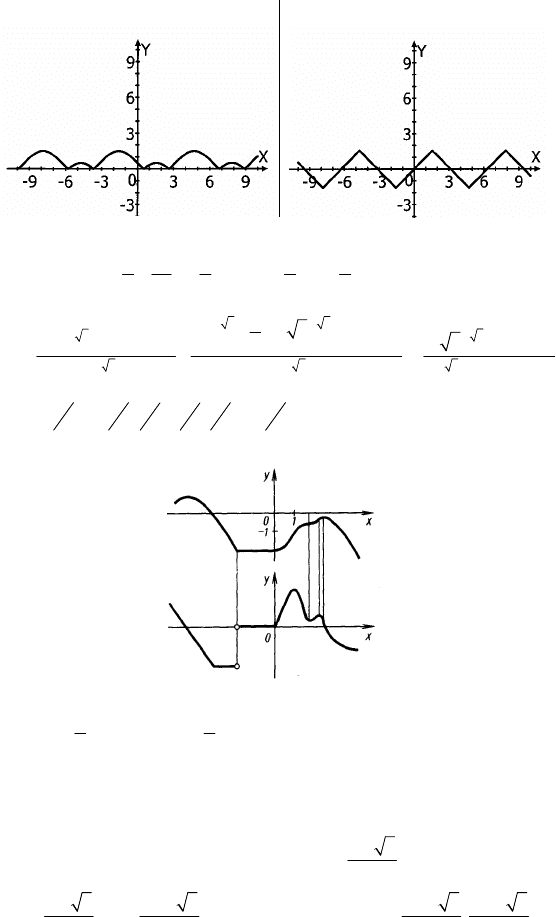
1.а)
б)
в) г)
д) е)
2.а) б)
143
в)
г)
ПС-10
1. а) f′(x) =
2
11 11
2sin cos 2sin cos
x
xx
x
xx x x
⎛⎞
+= +
⎜⎟
⎝⎠
; f′(0) = 0;
б)
() ()
4
3312
315
315 315
2
5+(3 2)
(( +2 ) )
== =
ln10 ( +2 ) ln10 ( +2 )
xxx
xx
x
y
xx xx
−−
−
−−
⎛⎞
−
′
⎜⎟
⎝⎠
′
31 2
31
5( 3 2 )
(2)ln10
x
x
xx
−−
−
−
+
;
в)
(
)
(
)
11
ln ln
222222
xx
x
xxx
y
′
=⋅=
.
2.
3. Подставим и увидим, что из равенств y
1
′′ = –2y
1
, y
2
′′ = –2y
2
следует,
что 3y
1
′′ +
1
4
y
2
′′ =
12
1
23
4
yy
⎛⎞
−+
⎜⎟
⎝⎠
.
ПС-11
1. а) x
4
+ 3x
3
+ 2x
2
+ 3x + 1 < 0; (x
2
+ 1)
2
+ 3x(x
2
+ 1) < 0; (x
2
+ 1)(x
2
+ 1) +
+ 3x(x
2
+ 1) < 0; (x
2
+1) (x
2
+1+3x) < 0. Поскольку всегда x
2
+1 > 0, то:
x
2
+3x+1 < 0; x
2
+3x+1=04; D=5 ⇒ x
1,2
=
35
2
±
−
⇒ x
2
+ 3x + 1 =
=
35 35
22
xx
⎛⎞⎛ ⎞
+−+
+−
⎜⎟⎜ ⎟
⎜⎟⎜ ⎟
⎝⎠⎝ ⎠
; x
2
+3x+1 < 0 при х ∈
3535
;
22
⎛⎞
−− −+
⎜⎟
⎜⎟
⎝⎠
;
144
б)
2
4121 27(1)0xxx x−−−−<. Решим уравнение:
2
4121 27(1)0xxx x−−−−=;
2
4181 61 27(1)0xxxxx x
−
−+ −− − =;
(
)
(
)
22 91 31 2 91 0xx x xx x−−+− −−=;
(
)
(
)
231 291 0xxxx+− −−=; 231 0xx
+
−= или 291 0xx
−
−=;
1
2
1
3
x
x
x
<
⎧
⎪
⎨
−=−
⎪
⎩
;
2
1
4
1
9
x
x
x
<
⎧
⎪
⎨
−=
⎪
⎩
; x = –3;
9
1
2
1
x
x
x
⎧
⎪
=
−
⎨
⎪<
⎩
;
2
01
81
(1 )
4
xx
x
x
><
⎧
⎪
⎨
=
−
⎪
⎩
;
997 81
8
1
x
x
⎧
−
⎪
=
⎨
⎪
<
⎩
. Решим неравенство. x ∈
997 81
3;
8
⎛⎞
−
−
⎜⎟
⎜⎟
⎝⎠
;
в)
2
2
tg 3
0
tg (1 tg )
x
xx
−
≥
−
;
(tg 3)(tg 3)
0
tg (1 tg )(1 tg )
xx
xx x
+−
≥
−+
;
tgx ∈
(
)
(
)
;3(1;0)1;3−∞ − ∪ − ∪ ;
x ∈
(
(
)
(
;;;
23 4 43
nn nn nn
ππ π ππ
⎤⎤
− +π − +π ∪ − +π π ∪ +π +π
⎦⎦
.
2. Заметим, что y = 1; минимум f(x), тогда y = 1 — первая касательная,
x
2
– 2x + 2 = 1; (x – 1)
2
= 0; x = 1, y = ax + b:
{
14
1
ab
ab
=
+
=
+
; тогда y=12x – 47
— вторая касательная.
ПС-12
1.
2--32
-2
(3 2 ) + ( )
()= =
xx
x
xxeexx
fx
e
−−
′
2
(3 2)+( )
=
x
xx
xe x x x
ee
−
−−
⎛⎞
−−
⎜⎟
⎜⎟
⎝⎠
=
x
x
e
(х
2
+2х–2)1; f′(x) = 0 при x = 0 и при x
12
=
212
2
−±
;
x
–∞; –1 –
3 –1 – 3 ; 0 0; –1 + 3 –1 + 3; +∞
f′
– + – +
x
min
= –1 ± 3 x
max
= 0; убывает на (–∞; –1 – 3] ∪ [0; 3– 1]; возраста-
ет на [–1 –
3
; 0] ∪ [
3
– 1; +∞).
2. f′(x) =
22
22 22
1 1 (1)(1)
( 1) ( 1) ( 1) ( 1)
xx
xx xx
+−−
+= =
+− +−
22
4
0
(1)(1)
x
xx
=
+−
;
x
min
= 0; x
max
= ±1;
–
11
–
+
0
+
–
x
–∞; –1
–1; 0 0; 1
1; +∞
f
1
tgx
+
–
10
+
–
+
3−
–
–
3
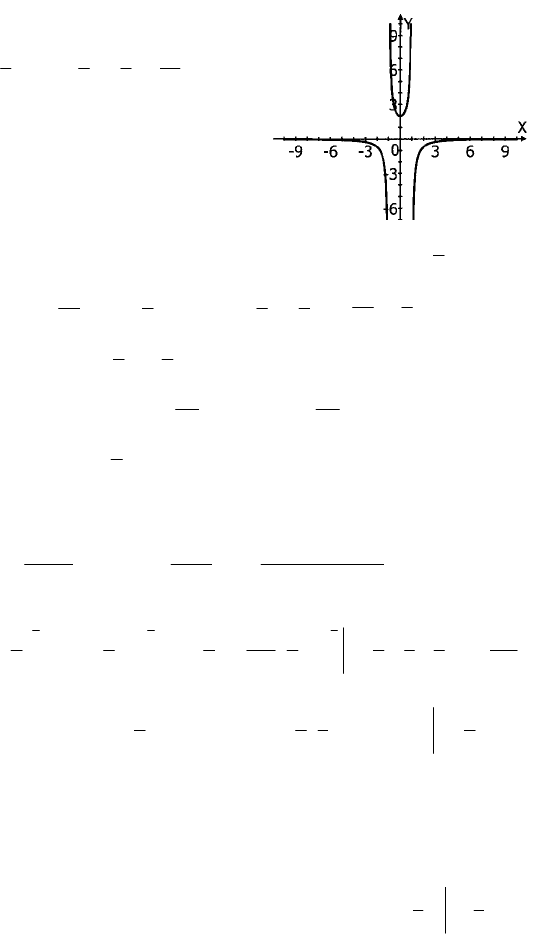
145
уравнение касательной имеет вид:
y = f′(x
0
)(x – x
0
) + f(x
0
);
y =
82822
(2)
9399
xx−+−=−−
;
ПС-13
1. f′(x)= –sinx –sin2x=0; sinx(1–2cosx)=0; sinx = 0 и cosx =
1
2
−
; x ∈ [0; π];
x = 0, π; x =
2
3
π
; f(0) =
3
2
; f(π) = –1 +
11
22
=
−
;
23
34
f
π
⎛⎞
=
⎜⎟
⎝⎠
; f(x) изменяет-
ся в пределах от
3
4
−
до
3
2
.
2. S = 2πr
2
+ 2πrh = 2πr
2
+
2V
r
; S′(r) = 4πr =
2
2V
r
; S′(r) = 0 при 4πr
3
= 2V,
откуда 2r = h, т.е.
2
h
r
=
.
ПС-14
1. –h′ = –e
x
cosx + e
x
sinx; f′ = e
x
cosx + e
x
sinx; сложим эти неравенства:
e
x
sinx =
2
f
h
′′
−
, т.е. F(x) =
sin cos
22
xx
fh e xe x
CC
−−
+
=+.
2. а)
22
14 14
33
22
111
22 2
xx x
dx d
−−
⎛⎞ ⎛⎞⎛⎞
+=+ +=
⎜⎟ ⎜⎟⎜⎟
⎝⎠ ⎝⎠⎝⎠
∫∫
14
5
3
5
2
3 2 6 5 6 192
182
52 535 5
x
−
⋅
⎛⎞
+=⋅=⋅=
⎜⎟
⎝⎠
;
б)
1
cos cos 2 (cos3 cos )
2
x
xdx x x dx
ππ
−π −π
=+=
∫∫
11 1
sin 3 sin 0 0
23 2
xx
π
−π
⎛⎞
+
==
⎜⎟
⎝⎠
.
3. Тк. f — четная, то f(–x) = f(x);
00 0
00
( ) ( ) () ( ) () ( )
aa
aa a
f
xdxfxdxftdtftdtafxdx
−− −
=−= −= =−
∫∫ ∫ ∫ ∫
.
4. Найдем точки пересечения линий y=x
2
и y = 4x – 4, y = 4x – 4 и y = 0;
x
2
–4x + 4 = 0; x = 2 и x= 1; тогда S = S
1
+ S
2
; S
1
=
2
2
23
0
0
18
33
xdx x
=
=
∫
;
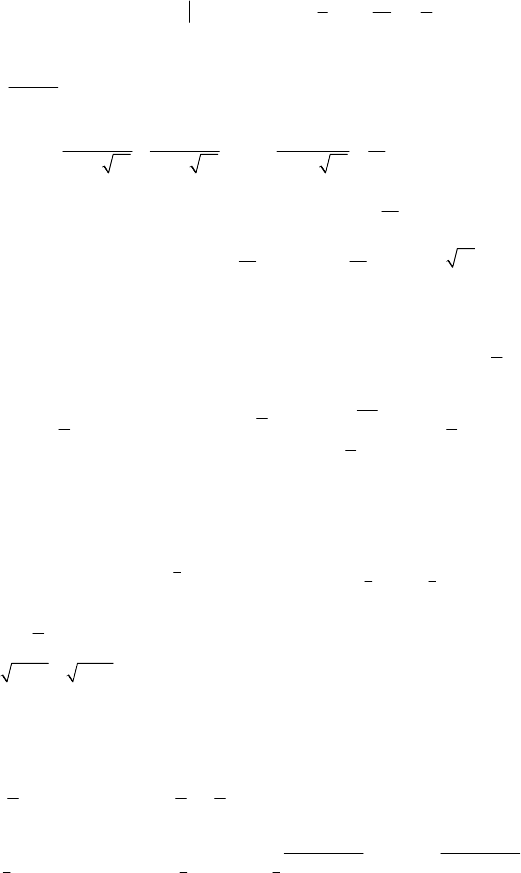
146
S
2
=
2
2
2
1
1
(4 4) (2 4 ) 2xdx x x−=− =
∫
, тогда S =
8142
24
333
+= =
.
ПС-15
1.
log log
log log log
log
N
bb
aN
bab
b
aa N==.
2.
10 10 10
310
10
10 10 10
log log log
11
log ...
2
log 10 log 10 log 10
xx x
x ++++=
;
log
10
x(1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10) =
11
2
; т.к. 1, 2, 3, ... —
арифметическая прогрессия, то
10
11 11
10log
22
x
⋅
=
, т.е.
10
10x = .
б) 3
x
+ log
2
x = 10; заметим, что при x = 2 равенство выполняется, но
слева функция монотонна, тогда других корней нет. Ответ: x = 2.
3.
lg 2
3
x
t
+
= ; t < 3t
2
– 2; 3t
2
– t – 2 > 0; (t – 1)
2
3
t
⎛⎞
+
⎜⎟
⎝⎠
> 0;
2
;(1;)
3
t
⎛⎞
∈−∞− ∪ +∞
⎜⎟
⎝⎠
;
lg 2
lg 2
2
3
3
31
x+
+
⎡
<
−
⎢
⎢
>
⎣
;
lg
lg
2
3
27
1
3
9
x
x
⎡
<−
⎢
⎢
>
⎢
⎣
;
lg
1
3
9
x
>
; lgx > –2;
x > 10
–2
= 0,01; x ∈ (0,01; +∞).
ПС-16
1. а) 2lg(lgx) = lg(3 – 2lgx);
2
lg 3 2 lg
lg 0
3
lg
2
x
x
x
x
⎧
⎪
=−
⎪
>
⎨
⎪
≠
⎪
⎩
;
3
2
2
10
1
lg 2 lg 3 0
x
x
xx
⎧
≠⎪
⎪
>
⎨
⎪
+
−=
⎪
⎩
;
22
33
1; 10 10 ;
(lg 3)(lg 1) 0
x
xx
⎧
⎛⎞⎛ ⎞
⎪
⎜⎟⎜ ⎟
∈
∪+∞
⎜⎟⎜ ⎟
⎨
⎝⎠⎝ ⎠
⎪
+−=
⎩
; x = 10;
б)
3
730xx+− +=;
23
(7)(3)
3
xx
x
⎧
+=+
⎨
>−
⎩
;
2
( 1)( 9 22) 0
3
xxx
x
⎧
−
++ =
⎨
>−
⎩
.
Ответ: x = 1.
2.
2
log ( 5
0,25
3) 1
252
2,5
525
xx− +−
⎛⎞ ⎛⎞
≤==
⎜⎟ ⎜⎟
⎝⎠ ⎝⎠
; –log
0,25
(x
2
– 5x + 8) ≤ 1;
2
11
44
log ( 5 8) 1 log 4xx−+≥−= ;
2
1
4
58
log 0
4
xx−+
≥
;
2
58
1
4
xx−+
≤
;
x
2
– 5x+4 ≤ 0; (x – 4)(x – 1) ≤ 0; x ∈ [1; 4]; ОДЗ: x
2
– 5x+8 > 0 для всех x.
Ответ: [1; 4].
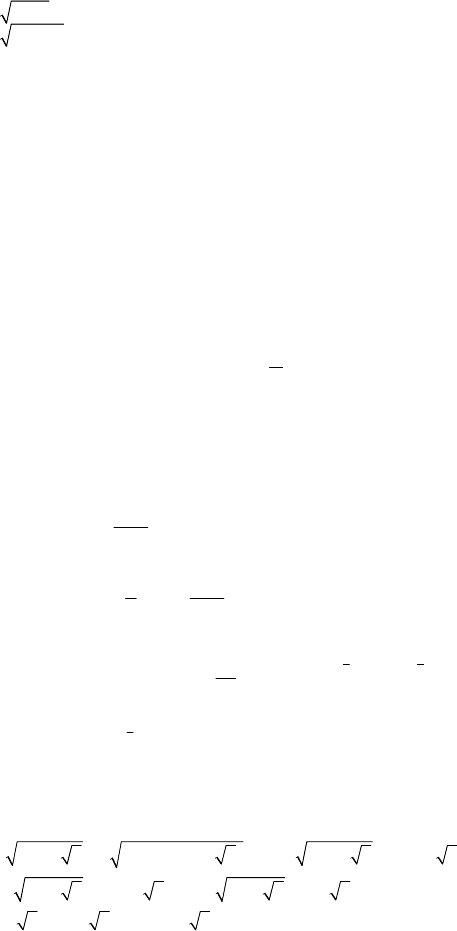
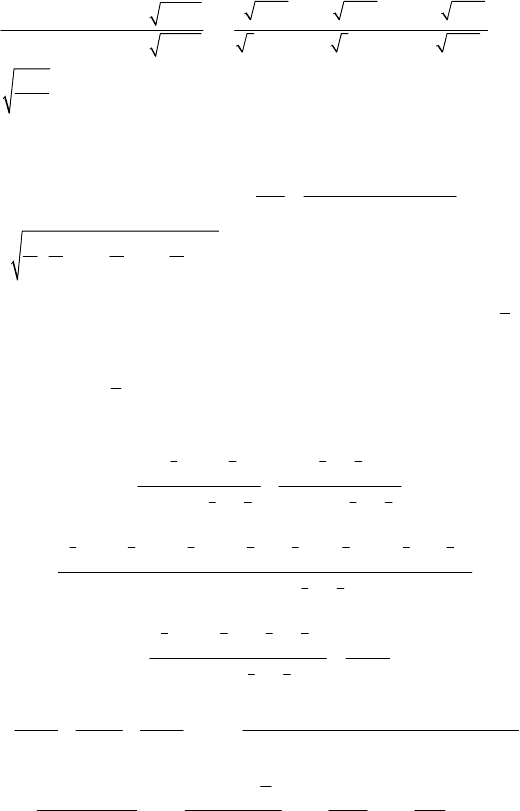
147
3.
4
4
22
0, 0
21
13
5
xy
x
yt
x
yr
tr
tr
>>
⎧
⎪
+=
⎪
+=
⎨
⎪
+=
⎪
+=
⎩
;
22
5
25 10 13
tr
rr r
=−
⎧
⎨
−
++=
⎩
;
r
2
– 5r + 6 = 0; (r – 3)(r – 2) = 0; r
1
= 3; t
1
= 2; r
2
= 3; t
2
= 3;
а) r = 3, t = 2;
{
16
21 81
xy
xy
+=
+=
;
{
16
(16 ) 60
xy
yy
=−
−
=
;
2
16
16 60 0
xy
yy
=−
⎧
⎨
−
+=
⎩
;
{
( 10)( 6) 0
16
yy
xy
−
−=
=−
;
(10, 6) = (x, y) = (6,10);
б) r = 3, t = 3;
{
24
21 16
xy
xy
+=
+=
;
{
5
61
xy
xy
=−
+
=
; не может быть, т.к. xy > 0.
Ответ: (10; 6) и (6; 10).
ПС-17
1. y′ = 4
x
ln4; y′ = yln4.
2. f′ = (f
ln(x)
(–x))′ = (e
h′xlng(x)
)′ =
ln
h
h
hg gf
g
⎛⎞
′′
+
⎜⎟
⎝⎠
.
3. F′(x) = e
x
(
)
(
)
iv iv v
44444 4444 4
x
R PPPP ePPPP P
′ ′′ ′′′ ′ ′′ ′′′
−+−+ + −++ + =
=
v
44 4
()=
xx
eP P eP+ ; т.к.
v
4
P = 0, т.к. многочлен не больше IV-ой степени.
ПС-18
1. f(0) = 0; f′ = 1 –
1
1
x
+
; при x > 0 f′ положительная, т.е. f — возрастает,
из этого следует, что f > 0 при x > 0; x – ln(1 + x) > 0; x > ln(1 + x).
2. F′(x) = ln2 ⋅ lnx +
21
11
ln
21
n
x
xC
n
+
+
+
+
.
3. x(t) = Cx(t), тогда x = C
1
e
Ct
,
найдем константы C
1
и C.
3
1
6
1
45
90
С
С
Су
Су
⎧
=
⎪
⎨
=
⎪
⎩
;
3
1
3
45
2
С
C
С e
e
⎧
=
⎪
⎨
=
⎪
⎩
; C
1
=
45
2
, тогда e
C
=
1
3
2 ;
3
2
t
Ct
e
=
.
Ответ:
3
() 22,5 2
t
xt =⋅.
Вариант 10
ПС-1
1. Возведем обе части в квадрат:
821025 2644(1025)821025 2045++−−++−+=−;
16 4 6 2 5 4(5 5)−− =−; 462555−− =−;
6251255625−− =− + = −
.
148
2. Пусть в день x ⋅ 100%, тогда (1 – x)
4
— за 4 дня.
(1–x)
4
=0,512(1–x); (1 – x)
3
= 0,512; 1 – x = 0,8; x = 0,2, тогда в день 20%.
3.
(
)
2
2
2( 3) 2 ( 3 2
(3)(2)(3) 4
2(( 3) 2 ( 3) 2)
(3)(2)(3) 4
tt t t t
tt t t
tt t t t
tt t t
+− +−+ −
−+−+ −
=
−=
−− +−+ −
+−−− −
=
2
2
t
t
+
−
−
при t = 5,2 выражение равно –1,5.
ПС-2
1. Рассмотрим теорему синусов, тогда стороны пропорциональны 12,
35, 37, пусть 1 — х см,
33
2
12 35 37 (см )
210 (см )
4418,5 (см)
abc x
S
R
−⋅−
== =
⋅
;
22 2 2
PP P P
S abc
⎛⎞⎛⎞⎛⎞
=−−−
⎜⎟⎜⎟⎜⎟
⎝⎠⎝⎠⎝⎠
; P =a+b+c= (12+35+37)x (см)=84 см.
2.
22
1292
||4
x
xxx
x
⎧
++>−− −
⎨
<
⎩
;
2
31030
||4
xx
x
⎧
+
+>
⎨
<
⎩
;
1
(3) 0
3
||4
xx
x
⎧
⎛⎞
⎪
+
+>
⎜⎟
⎨
⎝⎠
⎪
<
⎩
;
1
(4; 3) ;4
3
x
⎛⎞
∈− − ∪ −
⎜⎟
⎝⎠
.
ПС-3
1.
11
11
22
33
22
11
11
22
33
22
33
(3)( )(3)( )
ac b a bc
cabcab
−+
+
=
++ −+
=
1111
1111
422 24 2
3333
2222
1
1
22
3
2
3393 93
(3)(3)( )
ac bc ac b ac bc a bc
ccab
−−+++++
=
+−+
=
11
11
444
33
22
14
1
4
3
2
99 9
9
(9)( )
ac b a bc c
c
cab
+
++ +
=
−
−+
.
2.
22 4
122
0
121yy y
+−=
−+ −
;
22 4 2
22
( 2)( 1) 2( 1) 2( 2)
0
(1)(1)
yy y y
yy
+++−−+
=
−+
;
y
2
= t;
2
22
34
0
(1)(1)
tt
tt
+−
=
+−
;
2
4
(1)
3
0
1
tt
t
⎛⎞
−+
⎜⎟
⎝⎠
=
−
;
2
1
0
1
t
t
−
=
−
;
1
0
1t
=
+
— реше-
ний нет.
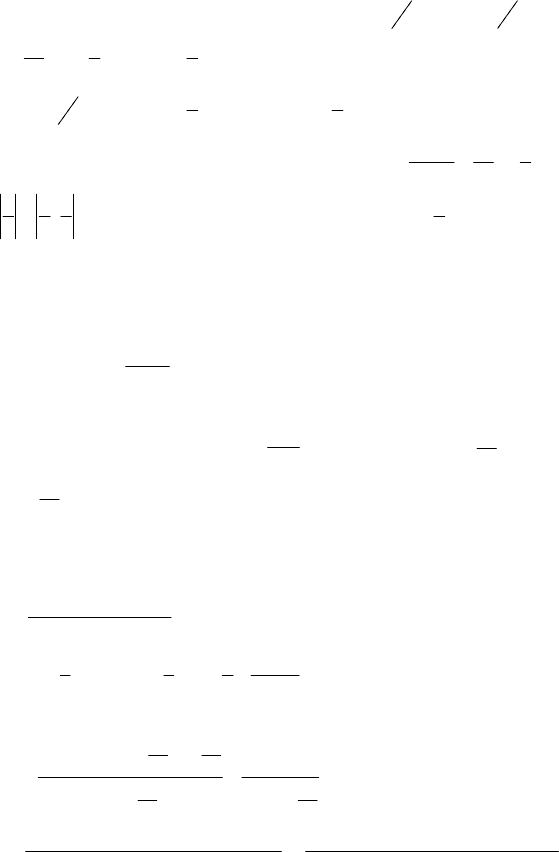
149
ПС-4
1. Сделаем замену: t=x
2
⇒ 2t
2
+5t+2=2(t
2
+
5
2
t+1); t
2
+
5
2
t+1=0;
D=
25 9
4
44
−=
⇒ t
1
=
1
2
−
; t
2
=2. Таким образом: 2x
4
+ 5x
2
+ 2 =
= 2(t
2
+
5
2
t+1)= =2
()
1
2
2
tt
⎛⎞
+
+=
⎜⎟
⎝⎠
22
1
2( )( 2)
2
xx
+
+=
22
(2 1)( 2)xx
+
+ .
2. 2b
2
x
2
– bx – 3 = 0; D = b
2
+ 24 b
2
= 25b
2
; x
1,2
=
2
531
;
2
4
bb
bb
b
±
=
− ; т.к.
131
2bb
<⋅
, то все корни меньше 1 по модулю при b ≥
3
2
.
3. x
2
– 2x – 2 = 0; D = 4 + 8 = 12 > 0 — корни существуют. Рассмотрим
теорему Виета: x
1
+ x
2
= 2; x
1
2
+ 2x
1
x
2
+ x
2
2
= 4; x
1
x
2
= –2; x
1
2
+ x
2
2
= 8;
x
1
4
+ 2x
1
2
x
2
2
+ x
2
4
= 64; x
1
4
+ x
2
4
= 56.
ПС-5
1. a
3
⋅ a
6
= 406;
9
4
6
2
a
a
−
=
; (a
1
+2d)(–a
1
+5d) = 406; a
1
+ 8d – 6 = 2a
1
+ 6d;
a
1
–2d = –6; a
1
= 2d – 6, тогда (4d–6)(7d–6)=406; 28d
2
–42d–24d+36=406;
28d
2
– 66d – 370 = 0; (d – 5)
18,5
0
7
d
⎛⎞
+
=
⎜⎟
⎝⎠
; a
1,1
= 4; a
1,2
=
79
7
−
; d
1,1
= 5;
d
1,2
=
37
14
, т.к. a
4
и a
9
— целые, то ответ: a
1
= 4, d = 5.
2. 3 + 33 + ... +
{
1992
1992
33 ... 3 3 1 11 ... 1111 3(1992 10 1991 ...)
⎛⎞
=
++ + = + ⋅ + =
⎜⎟
⎝⎠
142 43
=
1993
2
10 10 9 1991
3
9
−−⋅
⋅
.
3.
1
1
11996
12 ...
334
3
n
p
p
n
p
n
n
−
=
+
⎛⎞
+⋅+ = = −
⎜⎟
⋅
⎝⎠
∑
.
ПС-6
1. а)
1
2cos ... cos sin
sin
22
2sin 2 sin
22
nn
n
nn
+
αα
α⋅ ⋅ ⋅
α
=
αα
;
б)
sin 47 sin 61 sin11 sin 23
cos7
−°−°+°+°
=
°
2(sin 54 cos7 ) 2(sin18 cos 7 )
cos7
−
°°+ °°
°
=
= 2(sin18° – sin54°) = –1.
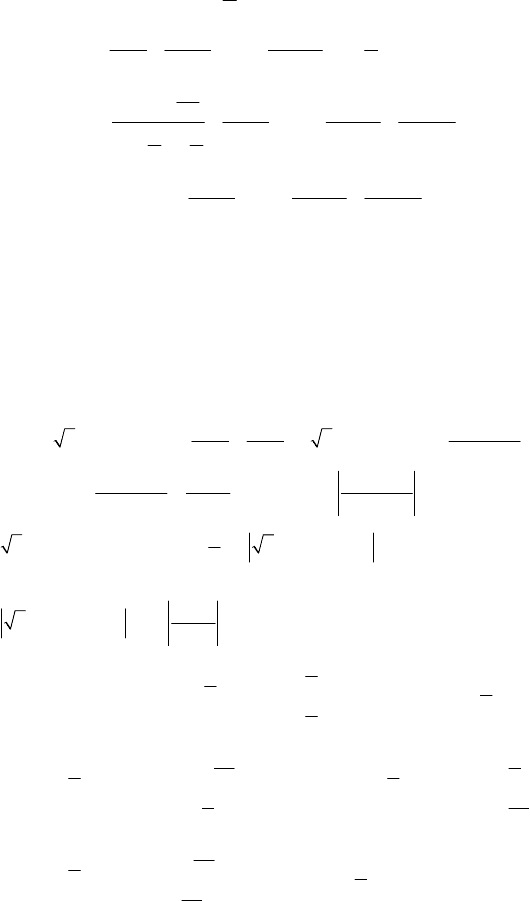
150
2.
cosec cosec2 ... ctg ctg2
2
n
α
α+ α+ = − α
.
11 1
... ctg ctg2
sin sin 2 2
sin 2
n
n
α
+++ −+α=
αα
α
=
2
12cos
11sin2
2
...
sin 2
sin 2 cos 2
2sin cos
22
n
nn
α
−
α
+
++ + =
αα
α
α
α
=
11sin2
ctg ... 0
sin 2
sin 2 cos2
n
nn
α
−α+ + + + =
α
αα
.
3. 3sinβ = sin(α + (α + β)); 3sinβ = sinα cos(α + β) + cosαsin(α + β);
3sinβ = sinαcosαcosβ – sin
2
αsinβ + sin(α + β)cosα;
3sinβ = –sinβ + sinβcos
2
α + sinαcosαcosβ + cosαsin(α + β);
2sinβ = cosαsin(α + β), тогда tg(α + β) = 2tgα; cosαsin(α + β) =
= 2sinαcos(α + β); 2sinαcos(α + β) = –2sin
2
αsinβ + 2sinαcosαcosβ =
= –2sinβ + 2sinβcos
2
α + 2sinαcosαcosβ = –2sinβ + 2cosαsin(α + β) =
= cosα(sin(α + β)).
ПС-7
1. а)
sin cos
2(sin cos )
cos sin
x
x
xx
x
x
+=+
;
1
2(sin cos )
cos sin
xx
x
x
+=
. Рас-
смотрим
12
cos sin sin 2
x
xx
=
, тогда
1
2
cos sinxx
≥
. Рассмотрим
2(sin cos ) 2sin
4
xx x
π
⎛⎞
+= +
⎜⎟
⎝⎠
. 2(sin cos ) 2xx
+
≤ , т.е. уравнение име-
ет решения, только если оно совпадает с решением системы:
2
2(sin cos ) 2, 2.
sin 2
xx
x
+= =
Решим систему:
sin 1
4
sin 2 1
x
x
⎧π
⎛⎞
⎪
+
=
⎜⎟
⎨
⎝⎠
⎪
=
⎩
;
2
4
4
x
n
x
k
π
⎧
=
+π
⎪
⎨
π
⎪
=
+π
⎩
; n, k ∈ Z;
2
4
x
n
π
=
+π
;
sin 1
4
sin 2 1
x
x
⎧π
⎛⎞
⎪
+=−
⎜⎟
⎨
⎝⎠
⎪
=
⎩
;
5
2
4
4
x
n
xk
π
⎧
=
−+π
⎪
⎨
π
⎪
=+π
⎩
;
sin 1
4
sin 2 1
x
x
⎧π
⎛⎞
⎪
+
=
⎜⎟
⎨
⎝⎠
⎪
=−
⎩
;
2
4
3
4
x
n
x
k
π
⎧
=
+π
⎪
⎨
π
⎪
=
+π
⎩
;
sin 1
4
sin 2 1
x
x
⎧
π
⎛⎞
⎪
+=−
⎜⎟
⎨
⎝⎠
⎪
=−
⎩
;
5
2
4
3
4
x
n
x
n
π
⎧
=
−+π
⎪
⎨
π
⎪
=+π
⎩
; тогда
2
4
x
n
π
=
+π
; n ∈ Z;
