Сапожников А.А. Решение самостоятельных и контрольных работ по алгебре и началам анализа за 11 класс
Подождите немного. Документ загружается.


151
б) 2sin7x +
3 cos3x + sin3x = 0; sin7x + sin 3
3
x
π
⎛⎞
+
⎜⎟
⎝⎠
= 0;
5sin7x + sin
3
5
x
π
⎛⎞
+
⎜⎟
⎝⎠
= 0; sin 5 cos 2 0
66
xx
ππ
⎛⎞⎛⎞
+
−=
⎜⎟⎜⎟
⎝⎠⎝⎠
;
5
6
x
n
π
+
=π
или
2
62
x
k
ππ
−±+π
, n, k ∈ Z;
30 5
x
n
π
π
=− +
или
32
x
k
π
π
=+
, n, k ∈ Z.
2. а) cosx – sinx – cos2x > 0; cosx – sinx – (cos
2
x – sin
2
x) > 0;
(cosx–sinx)–(cosx–sinx)(cosx + sinx) > 0; (cosx – sinx)(1 – cosx – sinx) > 0;
{
cos sin 0
1(cos sin) 0
xx
xx
−>
−+>
или
{
cos sin 0
1(cos sin) 0
xx
xx
−<
−
+<
;
3
2; 2
44
2;2( 1)
2
x
nn
xnn
⎧
ππ
⎛⎞
∈− +π +π
⎜⎟
⎪
⎪
⎝⎠
⎨
π
⎛⎞
⎪
∈+π π+
⎜⎟
⎪
⎝⎠
⎩
;
3
2; 2
44
2; 2
2
x
nn
xn n
⎧
ππ
⎛⎞
∈
+π +π
⎜⎟
⎪
⎪
⎝⎠
⎨
π
⎛⎞
⎪
∈π +π
⎜⎟
⎪
⎝⎠
⎩
;
3
2;2 2; 2
442
x
nn n n
πππ
⎛⎞⎛ ⎞
∈− +π π ∪ +π +π
⎜⎟⎜ ⎟
⎝⎠⎝ ⎠
; n ∈ Z
б)
5 2sin 6sin 1
x
x−≥−
; ОДЗ: 5 – 2sinx ≥ 0; sinx ≤
5
2
;6sinx – 1 ≤ 0 или
5 – 2sinx ≥ (6sinx – 1)
2
; sinx ≤
1
6
; 5 – 2sinx ≥ 36sin
2
x – 12sinx + 1;
11
arcsin 2 ; 2 arcsin 2
66
x
nn
⎛⎞
∈π− +π π+ +π
⎜⎟
⎝⎠
, sinx = t;
11
arcsin 2 ; arcsin 2 ( 1)
66
xnn
⎛⎞
∈π− +π +π +
⎜⎟
⎝⎠
,
12
sin sin 0
23
xx
⎛⎞⎛⎞
−
+≤
⎜⎟⎜⎟
⎝⎠⎝⎠
;
тогда sinx ≤
1
2
, т.е.
5
2; 2( 1)
66
xnn
ππ
⎡
⎤
∈− +π +π +
⎢
⎥
⎣
⎦
, n ∈ Z.
ПС–8
1. а) 8cos
2
x – 6cosx + 1 ≥ 0; cosx = t; 8t
2
– 6t + 1 ≥ 0;
(
)
(
)
5
1
cos cos 0
66
xx−−≥
;
11
arccos 2 ; arccos 2
44
xnn
⎡
⎤
∈
−+π++π∪
⎣
⎦
11
arccos 2 ; arccos 2 ( 1)
22
nn
⎡⎤
∪+π−+π+
⎣⎦
, n ∈ Z;
11
arccos 2 ; arccos 2 2 ; 2 ( 1)
4432
xnnnn
ππ
⎡⎤⎡⎤
∈− + π + + π ∪ + π − + π +
⎢⎥⎢⎥
⎣⎦⎣⎦
, n ∈ Z;
б)
1
8
11
48
0
log 0
log log 0
x
x
x
⎧
⎪
>
⎪
>
⎨
⎪
>
⎪
⎩
;
1
8
0
1
log 1
x
x
x
⎧
>
⎪
<
⎨
<
⎪
⎩
;
0
1
1
8
x
x
x
⎧
>
⎪
<
⎨
⎪
>
⎩
;
1
;1
8
x
⎛⎞
∈
⎜⎟
⎝⎠
;
152
в)
sin 2 0
cos 0
cos 1
x
x
x
>
⎧
⎪
>
⎨
≠
⎪
⎩
;
()
()
2
;
2
2; 2
22
xn
xn n
x
nn
⎧
≠π
⎪
⎪
π
∈π +π
⎨
⎪
ππ
∈− +π +π
⎪
⎩
; 2; 2
2
x
nn
π
⎛⎞
∈
π+π
⎜⎟
⎝⎠
, n ∈ Z.
2. а) f(–x) = –tg
3
x + sinx
5
= –f(–x) — нечетная;
б) f(–x) =
(1) 1 1
ln ln ln ( )
11 1
xx x
f
x
xx x
−+ + −
==−=−
−+ − +
—нечетная;
в) f(–x) = sincosx – cos(–sinx) = f(x) — четная.
3. Т.к. функция четная, то на [–
∞; 0] возрастает, тогда для всех
x
∈ (–∞; –2) f(x) < f(–2) = f(2); x ∈ (–2; 0) f(x) > f(–2) = f(2), тогда
x
∈ (–∞; –2) ∪ (2; +∞).
ПС–9
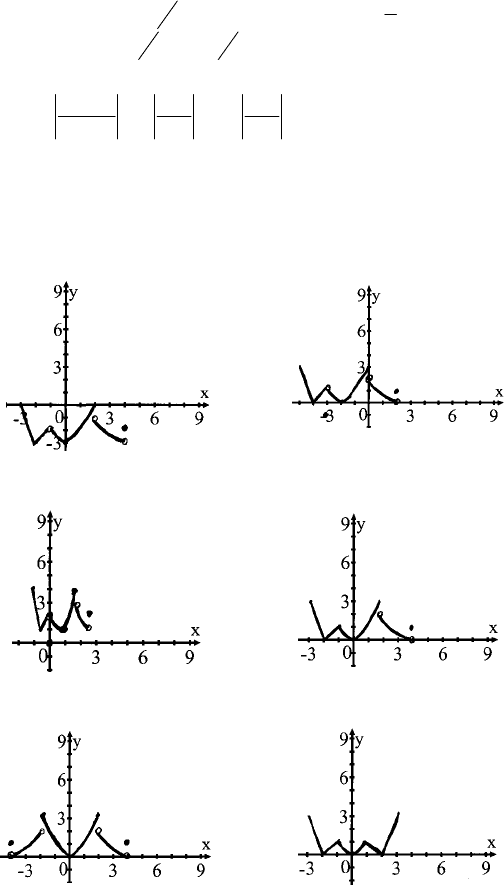
1.а)
б)
в)
г)
д)
е)
153
2.а)
б)
в) г)
ПС–10
1.а) y
′=|x| + (| x |)′ = 0; б) y′ =
()
()
15 15
15
(1) 14 (1)
12ln215(1)2ln2
xx
xx
−−
′
−⋅ =−⋅ ;
в) y
′ =
()
(
)
2
2
ln
ln ln ln
ln ln ln 1 ln 1
112ln2ln
x
x
xx
xx xx
xx
x
eex
xxxx
++
′
′
===
;
2.
3. Т.к. линейная комбинация решений является решением, то
12
1
4
3
yy−
— решение, что проверяется подстановкой.
154
ПС–11
1. а)
123
0
234xxx
+
−<
+++
;
( 3)( 4) 2( 2)( 4) 3( 3)( 2)
0
(2)(3)(4)
xx xx xx
xxx
+++++−++
<
+++
;
222
34122 48163 9618
0
(2)(3)(4)
xxx xxx xxx
xxx
++ ++ + ++− −−−
<
+++
;
410
0
(2)(3)(4)
x
xxx
+
<
+++
;
x
∈ (–4; –3) ∪ (–2,5; –2);
б) 4x
2
+12x 1
x
+ –27(1+x) < 0;4x
2
+ 18x 1 (6 1 27(1 )) 0xx x x
+
−+++<;
2x(2x + 9
1
x
+
)–3
1
x
+
(2x+9
1
x
+
)<0;(2x+9
1
x
+
)(2x–3
1
x
+
)<0;
Решим уравнение: (2x + 9
1
x
+
)(2x – 3
1
x
+
) = 0;
2
4
1
81
x
x
=
+ или
2
4
1
9
x
x=+ ; 4x
2
– 81x – 1 = 0 или 4x
2
– 9x – 9 = 0;
81 6571
8
x
±
=
;
(
)
3
(3)0
4
xx+−=
; ОДЗ: x > –1.
81 9 97
;3
8
x
⎛⎞
−
∈
⎜⎟
⎜⎟
⎝⎠
;
в)
()()
(tg 1)(tg 1)tg
0
3tg 3tg
xxx
xx
+−
≤
−+
;
tgx
∈ ( 3− ; –1] ∪ [0; 1] ∪ ( 3; +∞);
;; ;
34 4 32
x
nnnn nn
ππ π ππ
⎛⎤⎡⎤⎛⎞
∈ − +π − +π ∪ π +π ∪ +π +π
⎜⎜⎟
⎥⎢ ⎥
⎝⎦⎣⎦⎝⎠
, n ∈ Z.
2. Пусть прямая
y = ax + b касается f(x) в точке x
0
.
f(x
0
) = x
0
2
– 2x
0
– 3 = ax
0
+ b; f′(x
0
) = 2x
0
– 2 = a; т.к. прямая проходит
через
M, то –4 = b – a; 4 = a – b;
2
00 0
0
23
22
0
x
xaxb
xa
ab
⎧
−−=+
⎪
−=
⎨
⎪
−=
⎩
;
0
0
00
22
26
(3)(1)0
ax
bx
xx
⎧
=−
⎪
=−
⎨
⎪
+−=
⎩
, x
01
= +1; a
1
= 0; b
1
= –4; x
02
=–3; a
2
=–8; b
2
=–12, тогда
искомые касательные:
y = –4; y = –8x – 12.
x
–
4
–
3
–
+
–
2,5
–
2
–
+
+
4
3
−
–
+
3
–
+
+
8
657181 +
8
657181−
–
–
10
+
+
–
1
+
–
3− 3
155
ПС–12
1. f′(x) =
2
2
13
(4ln ) (2 ln 3ln )
x
xxx
xx
x
⋅+ − +
=
22
22
4ln 3 2ln 3ln ln 2ln 3xxxxx
xx
+
−− −+
==
;
f(x) = 0 при x =
1
e
;
x
ee= ; тогда x
min
=
1
e
; x
max
=ee, т.к. убывает на
1
0;
e
⎛⎤
⎜
⎥
⎝⎦
и
)
;ee
⎡
+∞
⎣
; возрастает на
⎥
⎦
⎤
⎢
⎣
⎡
ee
e
;
1
.
2.
f′(x) =
22
22 22
2( 1) ( 5)2 12
(1) (1)
x
xxxx
xx
−− +⋅ −
=
−−
;
f′(x) = 0 при x = 0; y = ax + b; f(2) =
8
3
−
;
825
33
ya≤− +
.
ПС–13
1. f′(x) = sin2x + cos2x; f′(x) = 0 при x
=
4
n
π
−+π
; тогда из значений
2
f
π
⎛⎞
−
⎜⎟
⎝⎠
,
4
f
π
⎛⎞
−
⎜⎟
⎝⎠
,
3
f
π
⎛⎞
⎜⎟
⎝⎠
,
4
f
π
⎛⎞
⎜⎟
⎝⎠
наи-
меньшее
12
2
−
, наибольшее
33
2
+
, т.е.
12
2
−
≤
f ≤
33
2
+
.
2.
2
3V
h
r
=
π
; S = πrl =
2
22 4
22
9V
rr h r
r
π+=π+
π
; f′(r) =
2
3
3
18
4
V
r
r
⎛⎞
π−
⎜⎟
⎜⎟
π
⎝⎠
;
f′(r) = 0 при V
2
=
2
2
4
18
r
π
, откуда
2
2
2
h
r
=
;
2
h
r
=
.
ПС–14
1. g′ = e
x
sinx + e
x
cosx; f′ = e
x
cosx – e
x
sinx;
2
g
f
′
′
−
= e
x
cosx = f, т.е.
F(x) =
(sin cos )
22
x
gf e x x
CC
−−
+= +
.
2. а)
3
44
3
2
00
14
(4 3) (4 3) (4 3) 132
315
xdx x d x
−−
−=−− −=−
∫∫
;
156
б)
111
sin sin 2 cos( ) cos3 (3 ) 0
232
xxdx xdx xdx
πππ
−π −π −π
=−−⋅ =
∫∫∫
.
3.
00 0
() () () ( ) () 0
aaaa a
aa
f x dx f x dx f x dx f x dx f x dx
−−
=+=−−=
∫∫∫∫∫
.
4. Найдем точки пересечения линий
x=2, x=–1, x=–2, т.к. x>–1, S=S
1
–S
2
;
S
1
=
2
2
232
1
1
181
( +4 +4) =( +2 +4 ) = +8+8 2+4=
333
xxdx xxx
−
−
−− −−−
∫
–3+16+2=15;
S
2
=
2
2
34
1
1
113
43
444
xx
−
−
==−=
∫
; S =
4
1
11 .
ПС–15
1.
(
)
11
ln log ln log 2
g
og
2
log 2
22
2
2
1
log 2
lo
l
2
22 20
x
x
x
x
x
e
x
ee
xxx−= − =− =
;
2. а)
||
1
2(|1||1|)
22
x
xx
−
=++−. При | x | > 1 левая часть ≤
1
2
, правая
меньше
1
2
при |x | ≤ 1, 2
–|x|
=
1
2
. Решим его:
1
||
2
1
22
2
x
−
−
==;
|
x | =
1
2
; x = ±
1
2
. Ответ: ±
1
2
.
б) 2
x
+ log
3
x = 9 при x = 3 получаем корень уравнения, т.к. 2
x
= log
3
x —
монотонная функция, то
x = 3 — единственный корень.
3.
2
cos
log sin 1
x
x > ;
2
,
cos sin ,
sin 0,
cos 0,
xn
x
x
x
x
≠π
⎧
⎪
>
⎨
>
⎪
≠
⎩
51 51
(2 ; arcsin +2 ) ( ; arcsin +2 )
22
x
nn n
−−
∈π π∪π− π
, n∈Z.
ПС–16
1. а) log
5
lg
2
x = log
5
(10 – 9lgx);
2
1
10 9lg 0
lg
10 9
x
x
xt
tt
≠
⎧
−
≥
⎪
⎨
=
⎪
=−
⎩
; t
2
+9t–10=0; D=121 ⇒ t
1
=1,
t
2
=–10 — не подходит. Поскольку: t=lgx=1, то x=10. Ответ: x=10.
б) 3
x
2
– 2x + 15 + 3x
2
– 2x + 8 + 2
22
(3 2 15)(3 2 8)xx xx
−
+−+= 49;
6
x
2
– 4x + 26 = 3x
2
– 2x + 13 =
222
(3 2 8) 49xx−−+−;
2
222
3280
(3 2 13) 3 2 8
xx
xx xx
⎧
−+≥
⎨
−+ = −+
⎩
;
x =
1
3
−
.
157
2.
sin 2
3
1cos2
11 1
22 2
x
x−
⎛⎞ ⎛⎞
<≤
⎜⎟ ⎜⎟
⎝⎠ ⎝⎠
;
sin 2 1
3
1cos2 2
x
x
>≥
−
. Решим первое неравенст-
во:
sin 2
3
1cos2
x
x
>
−
= ctgx; ;( 1)
6
xnn
π
⎛⎞
∈+ππ+
⎜⎟
⎝⎠
;
sin 2 1
ctg
1cos2 2
x
x
x
=
≥
−
;
(
)
;
3
x
nn
π
∈π +π ;
(
)
;
63
x
nn
ππ
∈+π +π.
3.
32
2
xy
t
x
−
=
;
1
2t
t
+=
; t
2
+ 1 = 2t; t
2
– 2t + 1 = 0; t = ±1, тогда
32
1
2
xy
x
−
=±
. Рассмотрим первый вариант:
32
1
2
xy
x
−
=
; x=2y; 4y
2
–18=
= 8
y
2
– 18y, получим x и y (3; 6);
32
1
2
xy
x
−
=
− . Ответ: (6; 3) (3; 15).
ПС–17
1. y′ = –2 ⋅ 3
–2x
ln3; y′ = –2yln3, тогда y′ + 2ln3y = 0.
2.
f′(x) = –e
–x
+ 1 при x > 0; f′(x) > 0, т.е. f(x) > f(0) для всех x > 0, т.е.
e
–x
> 1 – x.
3.
F′(x) = –e
–x
(–P
3
(x) – P
3
′(x) – P
3
′′(x) – P
3
′′′(x)) + e
–x
(–P
3
′(x) – P
3
′′(x) –
–
P
3
′′′(x) – P
3
IV
(x)); P
IV
= 0, т.к. многочлен степени не выше 3, тогда
F′(x) = f(x).
ПС–18
1. f(x) =
ln ( )
ln ( )
hx
g
x
; f′(x) =
2
ln ( ) ln ( )
() ()
() ()
ln ( )
gx hx
hx gx
hx gx
gx
′
′
−
.
2. Рассмотрим
f(x) =
ln
x
x
e ; f′(x) =
ln
2
1ln
x
x
x
e
x
−
; f′(x) = 0 при x = e, тогда
f′ > 0 на (0; e); f ∈ (0; f(e)]; f′(x) < 0; x > e; f ∈ (0; f(e)]. Ответ: (0; f(e)]
=
1
(0; ]
e
e .
3.
x(t) = Cx(t); x = C
1
e
Ct
; 15 = C
1
e
5C
; 60 = C
1
e
10C
; 4 = e
5C
, тогда C
1
=
15
4
;
e
5C
= 4; 5C = ln4; e =
ln 4
5
, тогда
ln 4
5
15
4
t
xe= .
ПРИМЕРНЫЕ КОНТРОЛЬНЫЕ РАБОТЫ
Контрольная работа № 1
Вариант 1
1.
2
1
Ff
x
′
=
= .
158
2.
F(x) = –4cosx + C; 00
2
FC
π
⎛⎞
=
−=
⎜⎟
⎝⎠
; C = 0; F = –4cosx.
3.
4
1
2
2
dx x
x
=−
∫
;
4
4
1
1
2
2844
dx x
x
=
−=−=
∫
.
4. а)
S =
3
3
23
0
0
119
262
xdx x==
∫
;
б)
S
1
=
2
2
23
1
1
11417
26366
xdx x==−=
∫
; S
2
=y(x
2
–x
1
)=
1
2
(2–1)=
1
2
; S=S
1
–S
2
=
=
712
623
−=
.
5.
S = S
1
+ S
2
.
S
1
=
2
2
3
3
0
8
2
2sin = 2cos = 2=3
2
xdx x
π
π
−+
∫
;S
2
=
2
2
3
3
0
8
3
sin = cos =
2
xdx x
π
π
−− −
∫
; S=
1
4
2
.
Вариант 2
1. F′ =
2
4
()
f
x
x
−= .
2.
F = 8sinx + C.
а)
F = 8sinx; б) F(π) = 0 = C.
3.
9
11
99
22
3
11
1
6
612361224
x
dx x dx x
x
−
===−=
∫∫
.
4. а)
S =
2
2
23
0
0
216
2
33
xdx x==
∫
;
б)
S
1
=
2
2
1
14
2
3
xdx=
∫
. S
2
= y(x
2
–x
1
)= 2(2–1)=2; S = S
1
– S
2
=
14 6 8 2
2
333 3
−==
.
5.
S=S
1
+S
2
;
S=
22 2
2
33 3
3
0
00 0
19
sin 2sin =3 sin = 3cos = 3( 1)=
22
xdx xdx xdx x
ππ π
π
−− − −−−
∫∫ ∫
.
Вариант 3
1. F′(x) =
2
13
()
2
f
x
x
+= .
2. а)
F(x) =
22
( ) 2 sin 3 sin 3 (3 ) cos3
33
f
xdx xdx xd x x C== =−+
∫∫ ∫
;
б)
F(π) =
2
0
3
C+=
; F(x) =
22
cos3
33
x−−
.
159
3.
2,5
4
4
3
1
1
3
63
x
dx x
x
==
∫
.
4. а)
2
2
23
2
2
1832
(4 ) 4 2 8
333
Sxdxxx
−
−
⎛⎞⎛⎞
=− =− =−=
⎜⎟⎜⎟
⎝⎠⎝⎠
∫
;
б)
1
1
23
1
1
1
1122
(4) 4 32
333
Sxdxxx
−
−
⎛⎞⎛⎞
=−+ =− + =− =
⎜⎟⎜⎟
⎝⎠⎝⎠
∫
;
S
2
= y(x
2
–x
1
)= 3(1–(–1))=6; S = S
1
– S
2
=
22 4 1
61
333
−= =
.
5.
S =
22
0
000
2cos 1 2 cos (cos 2 1) 2 6, 28
22
xx
dx x dx x dx
πππ
π
⎛⎞
+=+ =π+ +=π≈
⎜⎟
⎝⎠
∫∫∫
.
Вариант 4
1. F′(x) =
2
14
()
3
f
x
x
−= .
2. а)
F(x) =
33
( ) 3 cos 2 cos2 (2 ) sin 2
22
f
xdx xdx xd x x C== =+
∫∫ ∫
;
б)
F
4
π
⎛⎞
⎜⎟
⎝⎠
=
3
0
2
C+=
; F(x) =
33
sin 2
22
x
−
.
3.
9
11
9
22
1
1
612361224xdx x
−
==−=
∫
.
4. а)
()
3
3
23
3
3
1
(3 ) 3 3 3 3 2 4 3
3
Sxdxxx
−
−
⎛⎞
=− =+ =−=
⎜⎟
⎝⎠
∫
;
б)
1
1
23
1
1
1
116
(3 ) 3
33
Sxdxxx
−
−
⎛⎞
=− =− =
⎜⎟
⎝⎠
∫
. S
2
= y(x
2
– x
1
) = 2(1 –( –1)) = 4 ;
S = S
1
– S
2
=
16 4 1
41
333
−= =
.
5.
S =
2
00
(2sin 1) (2 cos ) 2
2
x
dx x dx
ππ
+=− =π
∫∫
.
Контрольная работа № 2
Вариант 1
1.
44
49 33 16 2−= =.
160
2.
1111 11
2222 22
11 1 1 11
22 2 2 22
()()
()
abab ab
ab a b ab
−+ −
=
+
.
3. а)
3
1
8
x =
;
1
2
x =
; б) 3x–2=16–8x+x
2
; x
2
–11x + 18 = 0; (x – 2)(x – 9) = 0;
x = 2, x = 9, т.к. 4 – 9 <0, то ответ: x = 2.
4.
(
)
(
)
()
8
2
xyxy
xy
⎧
+−=
⎪
⎨
−=
⎪
⎩
;
4
2
xy
xy
⎧
+
=
⎨
−
=
⎩
; 3x
=
, x = 9; 1y
=
, y = 1.
5.
2
cos 0
4
sin
5
2 2,5sin 1 sin
x
x
x
x
⎧
≥
⎪
≤
⎨
⎪
−=−
⎩
;
[2;2]
22
44
arcsin 2 ; arcsin 2 ( 1)
55
(1)
6
n
xnn
xnn
xn
ππ
⎧
∈− +π +π
⎪
⎪
⎪
⎡
⎤
⎨
∈π− + π + π +
⎢
⎥
⎪
⎣
⎦
⎪
π
∈− +π
⎪
⎩
;
6
x
n
π
=+π.
Вариант 2
1.
66
81 17 64 2−= =
.
2.
11 1
22 2
11 1
22 2
()()
()
ababab
aa b a
−+ +
=
−
.
3. а)
3
1
27
x =−
;
1
3
x =−
; б) 3x+1 = x
2
– 2x+1; x
2
– 5x = 0; x = 0, x = 5, т.к.
0 – 1 < 0, то ответ:
x = 5.
4.
(
)
(
)
()
21
7
xyxy
xy
⎧
−+=
⎪
⎨
+=
⎪
⎩
;
3
7
xy
xy
⎧
−
=
⎨
+
=
⎩
; 5x
=
, x=25; 2y
=
, y = 4.
5. sin
2
x = 2 – 2,5cosx = 1 – cos
2
x; cos
2
x – 2,5cosx + 1 = 0;
(cos
x – 2)
1
(cos )
2
x −
= 0; cosx =
1
2
;
2
3
x
n
π
=
±+π
, т.к. sin( ) 0
3
π
−
< , то
2
3
x
n
π
=+π.
Вариант 3
1.
44
95 14 81 3−= =.
2. Применим формулу для разности кубов:
13 13 23 13 13 23
23 13 13 23
13 13 13 13
()( )
()
ab a b a ab b
aabb
ab ab
−−++
==++
−−
.
