Sandau R. Digital Airborne Camera: Introduction and Technology
Подождите немного. Документ загружается.

2.4 Linear Systems 61
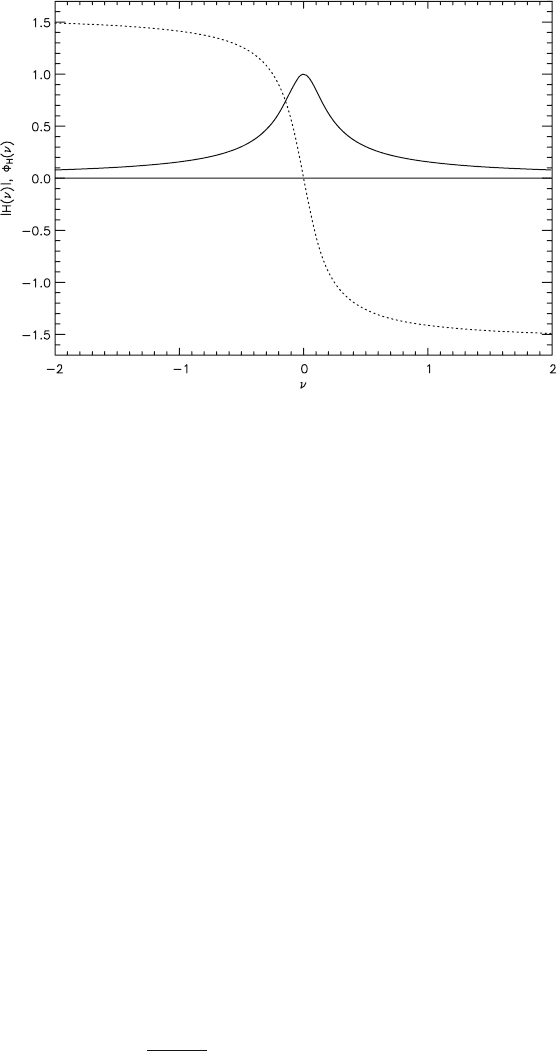
Fig. 2.4-4 Low-pass filter of first order. amplitude and phase response (dotted)(τ = 1)
It can be implemented as an electric R-C-circuit. Its frequency response
decreases very slowly with the frequency (∼ 1/ν). Filters with a steeper descent
(e.g. Butterworth filters) can be implemented with more complicated circuits.
In the two-dimensional case, which is important for optical imaging, the formulae
(2.4-3) and (2.4-7) change to
f
out
x
,y
=
h
x
−x,y
−y
·f
in
(
x,y
)
dxdy (2.4-15)
and
F
out
k
x
,k
y
= H
k
x
,k
y
·F
in
k
x
,k
y
. (2.4-16)
With a proper choice of the Equations (2.14-15) and (2.4-16), we can describe the
alteration of radiometric quantities (intensities, radiances etc.) by diffraction of light
at the aperture of an imaging system. But before the function h(x,y) for diffraction-
limited optical systems is introduced, we cover some more general considerations:
Let f
in
(
x,y
)
= δ
(
x −x
0
)
· δ
(
y − y
0
)
be the (idealized) intensity distribution of
a light emitting point in the object plane of an optical system. Then, in the image
plane, the intensity distribution f
out
x
,y
= h
x
−x
0
,y
−y
0
is obtained. The
function h(x,y) has a certain width because of diffraction. Therefore, the image of
the point (x
0
,y
0
) is spread over a certain area (or blurred) and the function h(x,y)is
called the Point Spread Function (PSF).
If the optical system has circular symmetry, then the function h depends only
on the distance r =
x
2
+y
2
from the principal axis, i.e. it has the property

62 2 Foundations and Definitions
h
(
x,y
)
= g
(
r
)
. In this case the image of the light emitting point has circular
symmetry around (x
0
,y
0
):
f
out
x
,y
= g
x
−x
0
2
+
y
−y
0
2
.
It can be shown that the frequency spectrum H(k
x
,k
y
) of a circular symmetric
function h(x,y) is circular symmetric too:
H
k
x
,k
y
= G
(
k
)
k =
k
2
x
+k
2
y
.
Now, let the periodic intensity distribution
f
in
(
x,y
)
= 1 + cos
2π
k
x
x +k
y
y
be given in the object plane. Unity is added to the cosine function because
radiation intensities cannot adopt negative values. Because it holds that
1 = cos
2π
k
0
x
x + k
0
y
y
with k
0
x
= k
0
y
= 0 , the function f
in
consists of two
periodic parts which are both transformed into the output distribution. In a similar
way to the one-dimensional case (see the remarks following (2.4-10)) the result
f
out
x
,y
=
|
H
(
0,0
)
|
+
H
k
x
,k
y
·cos
2π
k
x
x
+k
y
y
+
H
k
x
,k
y
is obtained.
This means that there is also a periodic intensity distribution in the image plane,
with, of course, different amplitude and phase. The function |H(k
x
,k
y
)| attenuates
the modulation of the sinusoidal intensity distribution and is therefore called the
Modulation Transfer Function (MTF). Because f
out
(as f
in
) cannot adopt negative
values, the MTF must fulfill the condition:
|
H
(
0,0
)
|
≥
H
k
x
,k
y
. (2.4-17)
The functions H(k
x
,k
y
) and
H
(k
x
,k
y
) are called the Optical Transfer Function
(OTF) and the Phase Transfer Function (PTF), respectively.
Now the circular symmetric case is considered in more detail. As was shown
above, in this case the OTF H(k
x
,k
y
) depends only on the spatial frequency k. Thus H
is a one-dimensional function. Furthermore, it can be shown that H(k
x
,k
y
) =G(k)isa
real-valued function. Let be G(k)<0fork
1
< k < k
2
. Then G(k) =|G(k)|·exp(jπ) and
H
(k) = π hold for k
1
< k < k
2
. Since cos(x+π ) = –cos(x), the intensity distribution
in the image plane becomes
f
out
x
,y
=
|
G
(
0
)
|
−
|
G
(
k
)
|
·cos
2π
k
x
x
+k
y
y
(k
1
<k<k
2
).
Thus there is contrast reversal in k
1
< k < k
2
. Bright parts of the input wave appear
dark and dark parts appear bright. Figures 2.4-5 and 2.4-6 illustrate this behaviour.

2.4 Linear Systems 63
Fig. 2.4-5 Contrast reversal: OTF und PTF (dashed)
Fig. 2.4-6 Contrast reversal: intensity profiles in object plane and image plane (dotted)fork = 2
In the range from k
1
= 1.5 to k
2
= 3, H(k) ≤ 0. At k = k
1
and k = k
2
the wave is
extinguished.
In the following discussion, the functions h(x,y) and H(k
x
,k
y
) are given and anal-
ysed for optical imaging with a thin lens (see Fig. 2.1-2). Let f
in
(x,y) = L
λ
(x,y) and
f
out
(x,y) = L’
λ
(x’,y’) be the spectral radiances in the object plane and the image
plane, respectively. Then these radiances are connected by the relationship
L
λ
x
,y
= L
λ
(
x,y
)
dxdy (2.4-18)

64 2 Foundations and Definitions
with
h
λ
x
,y
;x,y
= const ·
⎡
⎢
⎢
⎢
⎢
⎣
2
J
1
πD
λb
x
+
b
g
x
2
+
y
+
b
g
y
2
πD
λb
x
+
b
g
x
2
+
y
+
b
g
y
2
⎤
⎥
⎥
⎥
⎥
⎦
2
. (2.4-19)
Here J
1
is the Bessel function of first order. The function h
λ
is not shift-invariant.
The reason for this is the scaling (down) with the factor b/g and the reversal of the
coordinates. If one introduces new coordinates
X =−
b
g
x, Y =−
b
g
y
in the object plane, then the PSF h
λ
depends on
x
−X
2
+
y
−Y
2
and is
shift-invariant and circular-symmetric too.
The diffraction image of a light emitting point at (x
0
,y
0
) with the radiance
L
λ
(
x,y
)
= δ
(
x −x
0
)
· δ
(
y − y
0
)
is a circular spot (Airy spot) in the vicinity of
the point (x’
0
,y’
0
) with x
0
=−
b
g
x
0
, y
0
=−
b
g
y
0
. This spot is surrounded by
bright and dark rings which become weaker with increasing distance from (x
0
,y
0
)
(see Fig. 2.4-7).
The PSF
h
λ
(
r
)
= const ·
#
2
J
1
πD
λb
r
πD
λb
r
$
2
, r =
x
2
+y
2
(2.4-20)
Fig. 2.4-7 Airy spot; rings
enhanced for display
2.4 Linear Systems 65
has its first zero at
r
0
= 1.22
λb
D
. (2.4-21)
or for g >> f, b ≈ f at
r
0
= 1.22
λf
D
= 1.22 · λ · f
#
. (2.4-22)
The radius r
0
is a measure of the thickness of the Airy spot. It is proportional to
the wavelength λ: long-wave light is diffracted more strongly than short-wave light.
For λ → 0 the diffraction phenomena vanish. This is the limit of geometric optics.
Furthermore, r
0
increases with the f-number f
#
=f/D: lenses with smaller f-numbers
produce sharper images. This is well-known from photography.
Lenses with the PSF (2.4-20) are called diffraction-limited. Today’s real lenses
are generally not diffraction limited because of aberrations. Their blur is stronger
than that of diffraction-limited lenses.
With the aid of the PSF, the geometric resolution of an optical system can now be
defined. One can start from Rayleigh’s criterion for diffraction-limited resolution:
two point sources can be separated if the central maximum of the Airy spot of one
source has the position of the first minimum of the other source, i.e. if the distance
between the centres of the two Airy spots is equal to r
0
. Then, the separable light
sources have the distance r
0
·g/b in the object plane.
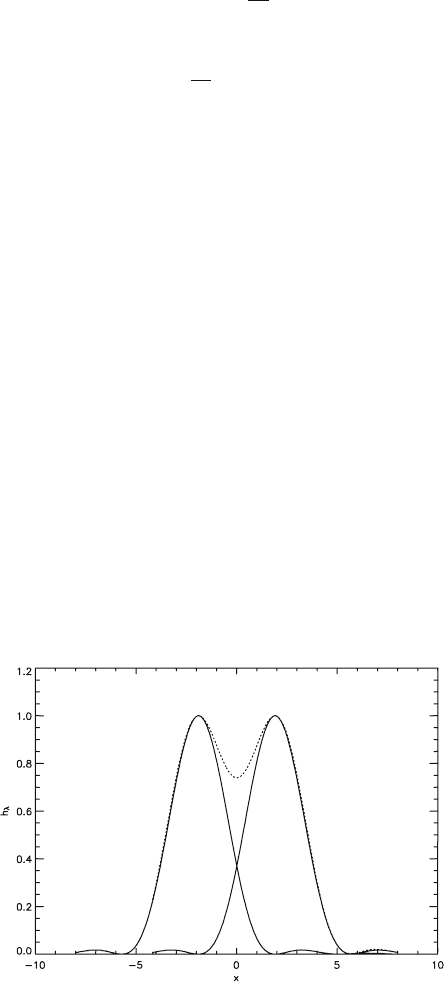
Figure 2.4-8 shows this case: the sum of the diffraction images of both points
(dotted) has a central recess with an intensity value of 0.74. This means that the cen-
tral value is lowered by about 26% with respect to the maximum. Such a difference
between maximum and minimum of the diffraction image is often very detectable,
which means that Rayleigh’s value r
0
does not provide the ultimate resolution of a
diffraction-limited optical system. Ultimately, the measurement precision (limited
by noise and quantisation errors) determins whether two points can be separated. If
Fig. 2.4-8 Geometric resolution according to Rayleigh

66 2 Foundations and Definitions
the signal-to-noise ratio is very good then two points with a distance much smaller
than r
0
can be separated if advanced methods of estimation theory are used. But
r
0
is a good measure for coarse estimates (as a rule of thumb). In the general (not
diffraction-limited) case, however, the PSF does not necessarily have a zero r
0
. Then
the geometric resolution may be defined by the distance d between two points for
which the function
a
λ
(
r
)
= h
λ
r −
d
2
+h
λ
r +
d
2
(2.4-23)
has the contrast
C =
max
{
a
λ
}
−a
λ
(
0
)
max
{
a
λ
}
= 0.26. (2.4-24)
The PSF of a diffraction-limited optical system has been given only up to a con-
stant factor (2.4-20), which describes the radiometric properties of the imaging that
have been discussed in Section 2.2 and which are not of interest here. Often const is
chosen so that
h
λ
(x,y)d
x
d
y
= 1
const =
π
4
D
λ·b
2
. Then the OTF is normalized
to H
λ
(
0,0
)
= 1.
The OTF of the normalized PSF (2.4-20) is given by
H
λ
k
x
,k
y
= G
λ
(
k
)
=
⎧
⎪
⎨
⎪
⎩
2
π
#
arccos
λb
D
k
−
λb
D
k ·
1 −
λb
D
k
2
$
0 elsewhere
for k ≤
D
λb
(2.4-25)
(see Fig. 2.4-9).
Fig. 2.4-9 MTF (=OTF) of a diffraction-limited optical system

2.4 Linear Systems 67
Formula (2.4-25) shows that the OTF (or MTF) vanishes for spatial frequencies
greater than the cut-off frequency
k
g
=
D
λb
. (2.4-26)
The optical system operates as an exact band-limited spatial low-pass filter. A
wavelike intensity distribution f
in
(
x,y
)
= 1 + cos
2π
k
x
x +k
y
y
in the object
plane cannot be seen in the image plane if the spatial frequency fulfills the con-
dition k =
k
2
x
+k
2
y
> k
g
. In other words, the distance = 1/k between two
wave peaks cannot be resolved if <1/k
g
holds. Thus a somewhat different defi-
nition of resolution via the smallest resolvable wavelength
g
= 1/k
g
can be given.
This is not far from the definition given above, because r
0
= 1.21·
g
. To mea-
sure the resolution, test images with thin lines on homogeneous backgrounds are
used. Let be the width of a line pair. Then a line pair cannot be resolved if
the number of line pairs per mm [lp/mm] (= k) is greater than a certain value
k
g
(in the case of diffraction-limited systems k
g
is given by (2.4-26)). Therefore,
the cut-off frequency k
g
defines the upper limit of line pairs per mm that can be
resolved.
If one does not use sinusoidal functions for the measurement of the MTF, but
instead makes use of patterns of rectangular stripes (which are easier to generate),
then one obtains not the MTF directly but a related function which is known as
the Contrast Transfer Function (CTF) (Holst, 1998b). The CTF is also an adequate
measure of the quality of an optical system.
To introduce the CTF, (2.4-15) is a convenient starting point. Let f
in
(x,y) = f
in
(x)
be a function which depends only on x (but not on y). Then it follows that f
out
too is
a function of x alone and that the two functions are related by
f
out
x
=
+∞
−∞
q
x
−x
·f
in
(
x
)
dx. (2.4-27)
Here
q
(
x
)
=
+∞
−∞
h
(
x,y
)
dy, (2.4-28)
is the so-called Line Spread Function (LSF), which is the reaction of the optical
system upon a line-shaped intensity distribution
f
in
(
x
)
= δ
(
x −x
0
)
.
The function c(x) is the response of the system (2.4-27) to an upright stripe
pattern of the following kind:
f
in
(
x,y
)
=
+∞
n=−∞
r
L
(
x − n
)
; = 2L. (2.4-29)
68 2 Foundations and Definitions
Here (a little bit different from (2.3-25))
r
L
(
x
)
=
1for −
L
2
≤ x ≤+
L
2
0 elsewhere
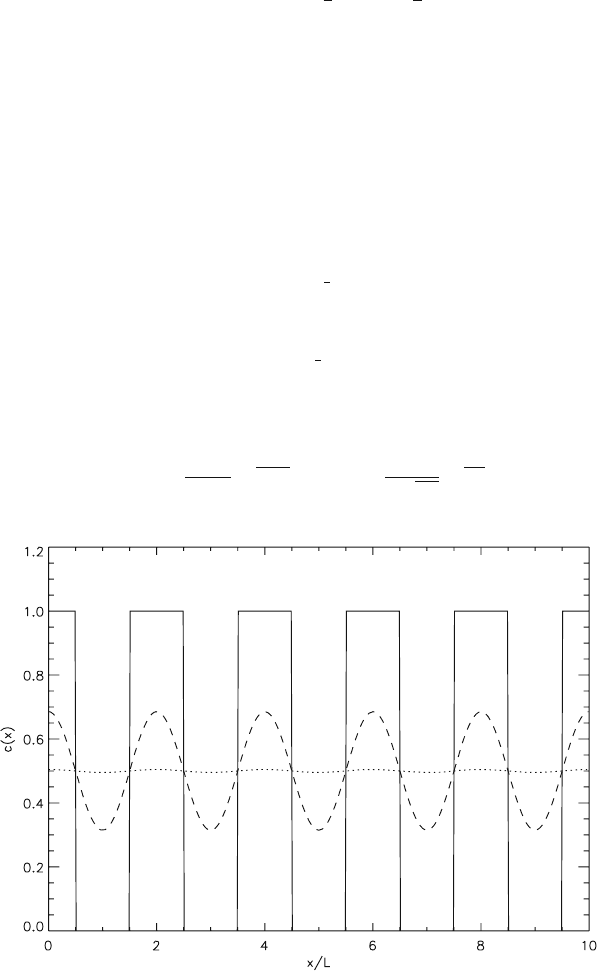
is the rectangle function and =2L is the period (or “wavelength”). A profile of the
function (2.4-29) is shown in Fig. 2.4-10 (solid line). Putting (2.4-29) into (2.4-27),
we obtain the following result (for f
out
(x) = c(x)):
c
(
x
)
=
+∞
n=−∞
q
n
(
x
)
. (2.4-30)
with
q
n
(
x
)
=
x−
2n−
1
2
L
x−
2n+
1
2
L
q
(
z
)
dz. (2.4-31)
An example for a Gaussian PSF or LSF
h(x,y) =
1
2πσ
2
e
−
x
2
+y
2
2σ
2
; q
(
x
)
=
1
σ
√
2π
e
−
x
2
2σ
2
Fig. 2.4-10 Stripe pattern response c(x)forσ = L/2 (dashed)andσ = L (dotted)
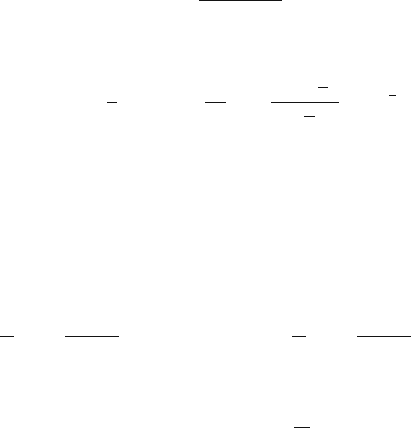
2.5 Sampling 69
is shown in Fig. 2.4-10. As mentioned above, the shape of the stripe pattern is not
maintained after transmission through the optical system. Furthermore, one realizes
that the contrast in the image plane almost vanishes for σ = L. The stripe pattern
response c(x) can be related to the OTF. Firstly, from (2.3-40) it follows that
q
(
x
)
=
Q
(
k
x
)
e
j2πk
x
x
dk
x
with Q
(
k
x
)
= H
(
k
x
,0
)
. (2.4-32)
Here, Q(k
x
) is the spectrum of the LSF (which, analogously to the MTF, could be
called the Line Modulation Transfer Function). Secondly, the quantities in (2.4-31)
can be written as
q
n
(
x
)
=
H
(
k
x
,0
)
·L
sin
(
πk
x
L
)
πk
x
L
·e
j2πk
x
x
·e
−j4πk
x
n
.
From (2.4-30) and (2.3-34) the following result is obtained:
c
(
x
)
=
1
2
+∞
n=−∞
H
n
2L
,0
·
sin
n
π
2
n
π
2
·e
jnπ
x
L
. (2.4-33)
This formula expresses the function c(x) through the OTF H(k
x
,k
y
) at the spatial
frequencies k
x
= n/2L, k
y
= 0.
Now it is easy to introduce the CTF. The contrast (or the modulation) of
the function c(x) is given by [max{c(x)}–min{c(x)}]/[max{r
L
(x)}+ min{r
L
(x)}]
= [max{c(x)}–min{c(x)}]. The CTF is the contrast as a function of the spatial
frequency k
x
= 1/2L. It can be calculated using (2.4-33). The result is:
CTF
(
k
x
)
=
4
π
·
∞
n=0
(
−1
)
n
2n + 1
·H
[
(
2n + 1
)
k
x
,0
]
=
4
π
·
∞
n=0
(
−1
)
n
2n + 1
·Q
[
(
2n + 1
)
k
x
]
.
(2.4-34)
Figure 2.4-11 shows the CTF for a diffraction-limited system with the OTF (2.4-
25) for some values of the cut-off frequency k
g
=
D
λb
.
2.5 Sampling
Thus far, one- or two-dimensional signals have been considered as continuous func-
tions of space and/or time. Now we must take into account that for signal processing
using digital computers a signal discretisation in space and/or time and in amplitude
is necessary. This means that continuous signals will be sampled at discrete space
or time points.
In the one-dimensional case the values f(t
n
) at the discrete points t
n
are extracted
from the continuous function f(t). The questions are whether or how much informa-
tion is lost because of sampling. It turns out that in the case of functions of finite
support (band-limited functions) there is no loss of information if the sampling inter-
val is small enough. Therefore, it can be useful (if aliasing must be avoided, see
below) to apply band-limiting filters before sampling.

70 2 Foundations and Definitions
Fig. 2.4-11 CTF for a diffraction-limited optical system (solid curve:k
g
= 150 mm
−1
, dotted
curve:k
g
= 100 mm
−1
, dashed curve:k
g
= 50 mm
-1
)
Let f(t) be a function with the finite spectrum F(ν) with cut-off frequency ν
g
:
F
(
ν
)
= 0for
|
ν
|
>ν
g
. (2.5-1)
Then the spectrum F(ν) can be continued in a periodic way and written as a
Fourier series. Let ν
s
be any frequency with ν
s
≥ ν
g
.If2ν
s
is used as period,
then, analogously to (2.3-9), inside the interval –ν
s
< ν <+ν
s
, F(ν) can be
represented as
F
(
ν
)
=
+∞
n=−∞
a
n
·e
−j 2 π
n
2ν
s
ν
(2.5-2)
with
a
n
=
1
2ν
s
+ν
s
−ν
s
F
(
ν
)
·e
j2π
n
2ν
s
ν
dν. (2.5-3)
Otherwise, the function f(t) may be written as the Fourier integral
f
(
t
)
=
+ν
s
−ν
s
F
(
ν
)
·e
j2πνt
dν (2.5-4)
with finite limits.
