Sandau R. Digital Airborne Camera: Introduction and Technology

Подождите немного. Документ загружается.

2.3 Fourier Transforms 41

Table 2.2-1 Radiometric and photometric quantities

Radiometric quantity Photometric quantity

radiant ﬂux 

rad

[W] luminous ﬂux 

phot

[lumen (lm)]

radiation intensity I

rad

[W/sr] luminous intensity I

phot

[candela (cd)]

irradiance E

rad

[W/m

] illuminance E

phot

[lux (lx)]

radiance L

rad

[W/m

·sr] luminance L

phot

[cd/m

]

2.3 Fourier Transforms

In many scientiﬁc disciplines and especially in investigations of optical systems,

it has turned out to be appropriate to understand functions of space and/or time

as superimpositions of sinusoidal functions. One reason is that the shape of sinu-

soidal functions is not changed by linear systems. Only amplitude (the modulation)

and phase are affected. Hence, important characteristics of optoelectronic systems

such as Optical Transfer Function (OTF) and Modulation Transfer Function (MTF)

have been introduced and these will be considered later (Section 2.4 covers linear

systems).

The one-dimensional case is considered ﬁrst. This is of interest in the study

of signal processing in electronic circuits. Let f(t) be a function of only one vari-

able t (which may be time or any other coordinate). Under certain mathematical

restrictions (which are not discussed here), the function f(t) can be written as a

superimposition of sinusoidal functions sin(2πνt) and cos(2πνt). Here, ν is the fre-

quency of the sinusoidal functions, which are periodic functions with the period

T = 1/ν. The frequency ν as a physical quantity is a non-negative real number

(0 ≤ ν < ∞).

It is more elegant to use the complex-valued exponential function

= cos

(

)

+j ·sin

(

)

, (2.3-1)

where j is the imaginary unit instead of the sinusoidal functions. Equation (2.3-1)

can be resolved to give

cos

(

)



−jx



;sin

(

)



−e

−jx



. (2.3-2)

Now, the Fourier representation of function f(t) can be written as

(

)

+∞



−∞

(

)

·e

j2πνt

dν. (2.3-3)

F(ν) is the (complex-valued) spectrum of the function f(t), which is deﬁned for

positive and negative “frequencies” ν. The occurrence of negative frequencies has

42 2 Foundations and Deﬁnitions

no physical meaning: it only guarantees mathematical elegance. Using (2.3-2), one

can transform (2.3-3) into a “physical” form with real valued quantities and non-

negative frequencies:

(

)

= 2

∞



(

)

·cos

[

2πν ·t +ϕ

(

)

]

dν. (2.3-4)

To obtain this formula, the complex-valued spectrum is written as

(

)

= A

(

)

·e

jϕ

(

)

; A

(

)

(

)

. (2.3-5)

Equation (2.3-4) is the representation of f(t) as a superimposition of sinusoidal oscil-

lations. Here, each oscillation of frequency ν has the amplitude 2A(ν) and the phase

shift ϕ(ν). Therefore, A(ν) is the amplitude spectrum and ϕ(ν) the phase spectrum

of the (real-valued) function f(t).

If the spectrum F(ν) is known, then the function f(t) can be calculated according

to (2.3-3). Inversely, the spectrum can be computed as

(

)

+∞



−∞

(

)

·e

−j2πνt

dt, (2.3-6)

if f(t) is given. The signals f(t) considered here are real-valued functions.

For such functions the following symmetry relationships can be derived from

(2.3-6):

∗

(

)

= F

(

−ν

)

;

(

)

(

−ν

)

; ϕ

(

)

=−ϕ

(

−ν

)

. (2.3-7)

Here, F

∗

is the complex conjugate of F. Equation (2.3-7) characterises the fact

mentioned above that non-negative frequencies are sufﬁcient for the description of

a real-valued signal f(t).

A special class of functions f(t) comprises of the periodic functions with

(

t +T

)

= f

(

)

. (2.3-8)

T is the period of the function. The functions f(t) considered up to this point can

be interpreted as a special case of periodic functions with T →∞.

The periodic functions can be represented as a superimposition of sinusoidal

functions with the discrete frequencies n·ν = n/T. The functions sin(2πνt) and

cos(2πνt) are periodic with T = 1/ν. The same is true for the functions sin(2πnνt)

and cos(2πnνt) and also for every linear combination of those functions. The func-

tions sin(2πnνt) and cos(2πnνt)(n = 0,...,∞) represent a fully orthogonal system

of functions. Each periodic function can be represented as a superimposition of that

system.

2.3 Fourier Transforms 43

As for the Fourier integrals, the expansion of periodic functions f

(t) in terms of

exponential functions is more elegant:

(

)

+∞



n=−∞

·e

j2π

. (2.3-9)

Equation (2.3-9) is the Fourier series of the periodic function f

(t).

The orthogonal property of the basis functions exp(j2πnt/T) is expressed by the

relationship

+T/2



−T/2

j2π

n−m

dt = T ·δ

n,m

. (2.3-10)

Here, δ

n,m

is the Kronecker symbol deﬁned by

n,m



1forn = m

0forn = m

. (2.3-11)

Using (2.3-10) the expansion (2.3-9) can be inverted with the result

+T/2



−T/2

(

)

·e

−j2π

dt, (2.3-12)

which is the analogue of (2.3-6). The Fourier coefﬁcients that describe the discrete

spectrum of the periodic function f

(t) obey the symmetry relation

∗

= a

−n

, (2.3-13)

which is the analogue of (2.3-7). As for F(ν), one can introduce (discrete) amplitude

and phase spectra according to

·e

jϕ

. (2.3-14)

Next, we present some properties of Fourier integrals and Fourier series. Let F(ν)

be the spectrum of a function f(t). Let G(ν) be a spectrum which differs from F(ν)

by a linear phase shift:

(

)

= F

(

)

·e

−j2πνt

. (2.3-15)

Then, according to (2.3-3), the corresponding functions f(t) and g(t) are related by

(

)

= f

(

t −t

)

, (2.3-16)

which means that a linear phase shift corresponds to a time shift of the signal.

Furthermore, a pure time shift of a signal f(t) does not change the amplitude

spectrum of that signal. In the periodic case the same is true: multiplication of

44 2 Foundations and Deﬁnitions

the Fourier coefﬁcients a

by a linear phase exp(–j2πnνt

) is equivalent to a time

shift t

If f(t) is a voltage or a current then f

(t) is proportional to the electrical power.

The integral over f

(t) is therefore proportional to the total energy contained in the

signal. The following relationship holds (Parseval theorem):

+∞



−∞

(

)

dt =

+∞



−∞

(

)

dν. (2.3-17)

The total energy is decomposed into spectral parts |F(ν)|

dν. |F(ν)|

, therefore,

is called the power spectrum (energy spectrum would be better). In the periodic case

the analogous formula is

+T/2



−T/2

(

)

dt =

+∞



n=−∞

. (2.3-18)

One derives (2.3-18) by inserting the Fourier series into the left hand side and

using the orthogonality relationship (2.3-10). Analogously, (2.3-17) can be derived

if one uses the Dirac delta function δ(t) instead of the Kronecker delta. One can

envisage this function (mathematically not correct!) as an inﬁnitely narrow signal

with an inﬁnitely large signal value concentrated at t = 0:

δ(t) =



∞

for t = 0

elsewhere

The δ-function is normalized to unity and cuts a single value out of a continuous

function f(t):

(

)

+∞



−∞







·δ





−t





; especially:

(

)

+∞



−∞

(

)

·δ

(

)

dt and

+∞



−∞

(

)

dt = 1.

(2.3-19)

There are many representations of the δ-function as a boundary value of contin-

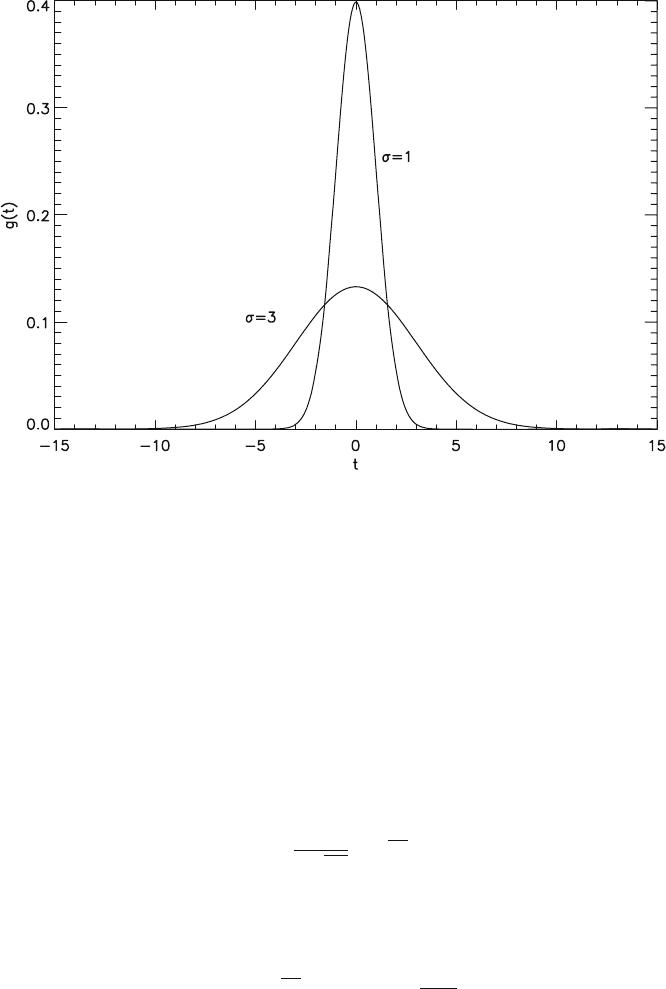
uous funct-ions, for instance as a Gaussian with vanishing width (see Fig. 2.3-1):

(

)

lim

√

2π

·e

−

2σ

σ → 0

. (2.3-20)

If the Fourier transform (2.3-6) is applied to the δ-function, then from (2.3-5) it

follows that:



(

)

= 1 for −∞<ν<+∞ (2.3-21)

2.3 Fourier Transforms 45

Fig. 2.3-1 Gaussian

and

(

)

+∞



−∞

j2πνt

dν. (2.3-22)

The spectrum of the δ-function contains arbitrarily high frequencies with con-

stant amplitude, which is not possible in reality. The δ-function is a mathematical

abstraction which does not represent a real signal. But it has many mathematical

advantages, which can be used to derive formulae such as (2.3-17).

Another important function is the Gaussian (or normal distribution, see

Fig. 2.3-1), which is often used for the description of optoelectronic signals:

g(t) =

√

2π

·e

−

2σ

. (2.3-23)

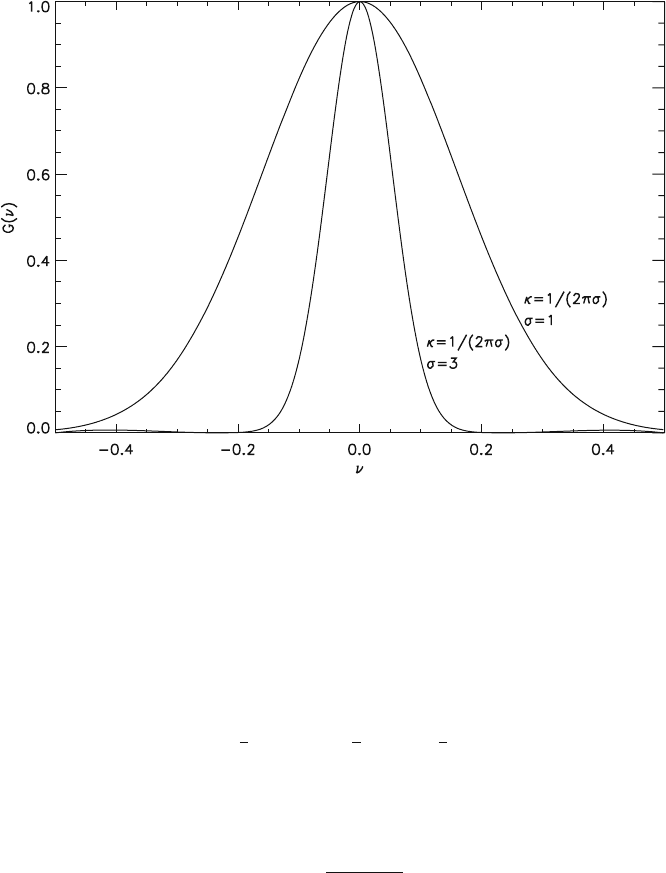
Its spectrum is given by

(

)

= e

−

2κ

with κ =

2πσ

. (2.3-24)

The spectrum of a Gaussian, therefore, is also a Gaussian but with another nor-

malisation. The parameter σ describes the width of the bell-shaped function g(t),

46 2 Foundations and Deﬁnitions

Fig. 2.3-2 Spectrum of Gaussian

whereas κ characterises the width of G(ν). The relationship 2πσκ = 1 ( 2.3-24)

means that the broader the spectrum G(ν), the narrower is the signal g(t) and con-

versely (see Fig. 2.3-2). In other words, the narrower and steeper a function, the

greater the frequencies it must contain. This holds in general and not only for a

Gaussian.

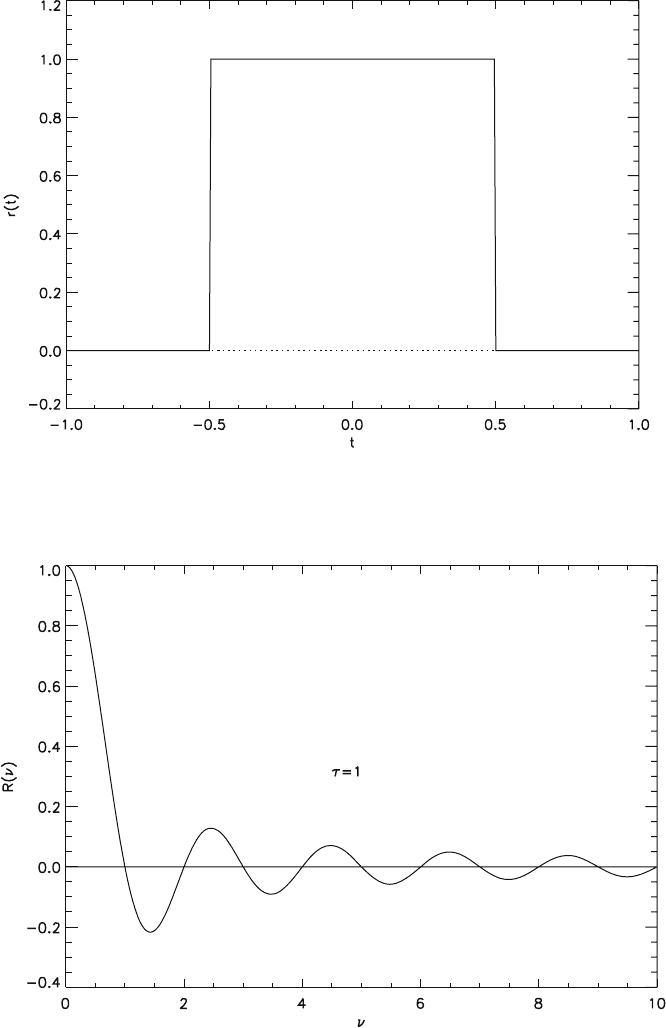
Another function used in the following is the “rectangular” function

(

)



for −

≤ t ≤+

0 elsewhere

(2.3-25)

with the width τ (Fig. 2.3-3). Its spectrum is given by

(

)

sin

(

πντ

)

πντ

(2.3-26)

(see Fig. 2.3-4). This spectrum decreases very slowly with increasing frequency

(proportional to 1/ν) owing to the discontinuities of r

(t). This behaviour is also

expressed by zeroes ν

= n/τ of R

(ν). The smaller τ is, the bigger are the zeroes.

Not only s inusoidal functions but also other periodic functions play an important

role in the description of signals. Before special cases are addressed, however, a

general relationship between continuous and discrete signal representations is given.

2.3 Fourier Transforms 47

Fig. 2.3-3 Rectangular function (τ = 1)

Fig. 2.3-4 Spectrum of the rectangular function (τ = 1)

48 2 Foundations and Deﬁnitions

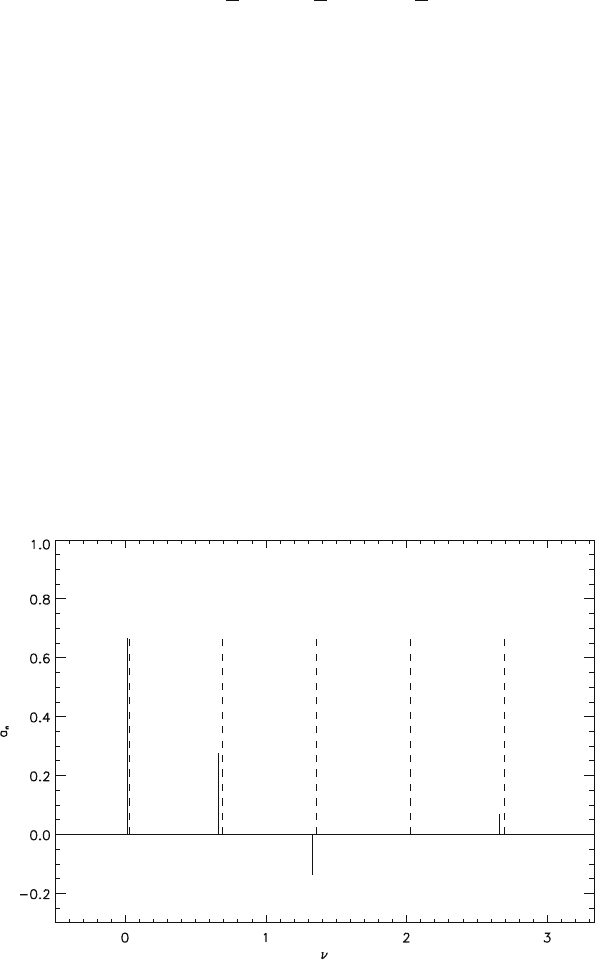
Fig. 2.3-5 Periodic rectangular signal (τ = 1, T = 1.5) and Dirac-comb (dashed)

A periodic signal can be written as the periodic continuation of a function f

(t),

which is concentrated in the interval [–τ /2, +τ /2] (i.e. f

(t) = 0fort /∈ [–τ /2, +τ /2])

(Fig. 2.3-5):

(

)

+∞



n=−∞

(

t −nT

)

; T ≥ τ . (2.3-27)

Here, the period T is always greater than or equal to the width τ of the function

(t). According to (2.3-6), the spectrum F

(ν) of the function f

(t) can be written as

(

)

+τ/2



−τ/2

(

)

·e

−j2πνt

dt.

Otherwise, according to (2.3-12), the Fourier coefﬁcients are

+T/2



−T/2

(

)

·e

−j2π

dt =

+τ/2



−τ/2

(

)

·e

−j2π

dt.

The comparison of these two formulae shows that the Fourier coefﬁcients can be

expressed through the spectrum F

(ν) at the sampling points ν = n/T:

·F





. (2.3-28)

The periodic function f

(

)

can therefore be represented as the Fourier series

(

)







·e

j2π

. (2.3-29)

2.3 Fourier Transforms 49

From (2.3-6) the spectrum of the periodic function f

(

)

is given by

(

)







·δ



ν −



. (2.3-30)

As is the case with the periodic functions f

(

)

, their spectra F

(

)

can be

represented by a deﬁned number of quantities. This is also important in connection

with the band-limited signals considered in Section 2.5.

We turn now to some special cases of periodic signals. For the description of

time-discrete signals and especially for the sampling of continuous signals, periodic

continuations of rectangular functions are used (Fig. 2.3-5):

(

)

+∞



n=−∞

(

t −nT

)

; T ≥ τ . (2.3-31)

The individual rectangles of the periodic signal (2.3-31) have the amplitude 1/τ .

So, in the limit τ → 0 with

(

)

= lim r

(

)

τ → 0

(2.3-32)

the so-called Dirac comb can be introduced:

(

)

+∞



n=−∞

(

t −nT

)

, (2.3-33)

v = 0/ T v = 1/ T v = 2/ T v = 3/ T v = 4/ T

Fig. 2.3-6 Fourier coefﬁcients for periodic rectangular function and Dirac-comb (dashed)

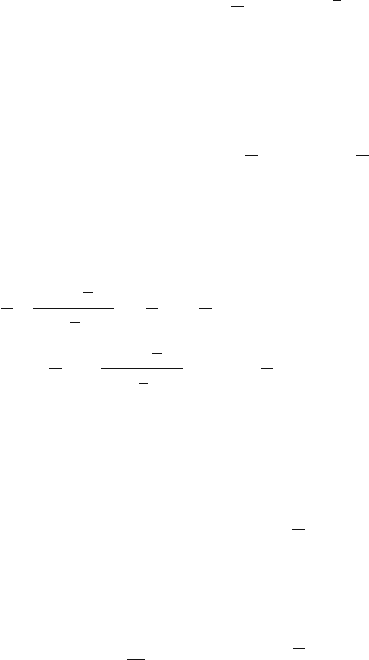
50 2 Foundations and Deﬁnitions

which is the periodic continuation of the delta function and the limit of (2.3-31) for

τ → 0.

According to (2.3-9) the periodic function δ

(

)

can be represented by the Fourier

series

+∞



n=−∞

(

t −nT

)

+∞



n=−∞

j2π

. (2.3-34)

This formula is a special case of (2.3-29) and is useful for many investigations of

signals. The spectrum of the Dirac comb is given by



(

)



−j2πnTν





ν −



. (2.3-35)

Using these formulae and the spectrum R

(ν) (2.3-26), we obtain the following

results for the periodic continuations of rectangular functions (2.3-31):

sin









(Fourier coefﬁcients) (2.3-36)

(

)



sin





·δ



ν −



(spectrum). (2.3-37)

Periodicities can appear not only in the function f(t) but also in the spectrum

F(ν). Let F

(ν) be a periodic spectrum with the period ν

. Then the equation F

(ν

+ ν

) = F

(ν) holds. Similarly to (2.3-29) and (2.3-12), the periodic spectrum can

be described by the Fourier series

(

)



·e

−j2π

(2.3-38)

with the Fourier coefﬁcients

+ν



−ν

(

)

·e

j2π

dν. (2.3-39)

This description will be helpful for the derivation of the sampling theorem

(Section 2.5).

Following these representations of one-dimensional Fourier integrals and Fourier

series, the two-dimensional case can now be addressed very brieﬂy.

Let f(x,y) be a function of two variables x and y. Then, analogously to (2.3-3) and

(2.3-6), the 2D Fourier transform is deﬁned by

(

x,y

)

=·e

j2π

(

x+k

)

(2.3-40)





=·e

−j2π

(

x+k

)

dxdy. (2.3-41)