Sandau R. Digital Airborne Camera: Introduction and Technology
Подождите немного. Документ загружается.


2.3 Fourier Transforms 51
Here, the integrals are taken from –∞ to +∞. The variables k
x
, k
y
are the spatial
frequencies and F
k
x
,k
y
is the spatial frequency spectrum of the function f(x,y).
With the introduction of the amplitude and phase spectra according to
F
k
x
,k
y
=
F
k
x
,k
y
·e
j
(
k
x
,k
y
)
(2.3-42)
one can obtain a representation with non-negative spatial frequencies:
f
(
x,y
)
= 2
∞
0
∞
0
F
k
x
,k
y
·cos
2π
k
x
x +k
y
y
+
k
x
,k
y
dk
x
dk
y
. (2.3-43)
This description gives a clear interpretation of the spatial frequencies. The func-
tion cos
2π
k
x
x + k
y
y
+
k
x
,k
y
is a wave with peaks and valleys. If the phase
shift , which characterises only the shift of the wave with respect to the point
x = 0, y = 0, is neglected, then the peaks are given by cos
2π
k
x
x +k
y
y
= 1
or by the equations k
x
x + k
y
y = n
(
n = 0, ±1, ...
)
. If one introduces the wave
vector (or spatial frequency vector) k =
k
x
,k
y
and the position vector r =
(
x,y
)
,
then this equation can be written more compactly as k · r = n . These equations
describe a variety of straight lines (see Fig. 2.3-7) which are perpendicular to the
wave vector k. The distance between two straight lines n and n +1isgivenbythe
“wavelength” = 1/k . Here, k =
k
2
x
+k
2
y
is the length of the wave vector.
The equation = 1/k is the equivalent of the equation T = 1/ν (T is period, ν
is frequency) which characterises the sinusoidal oscillations. This justifies the term
spatial frequency for k. The components k
x
and k
y
of the wave vector describe the
actual spatial frequency k and the wave direction ϑ = arctan
k
y
/k
x
.
y
x
ϑ
k
n = 0
n = 1
n = 2
Λ
Fig. 2.3-7 Wave peaks and
valleys (dashed)
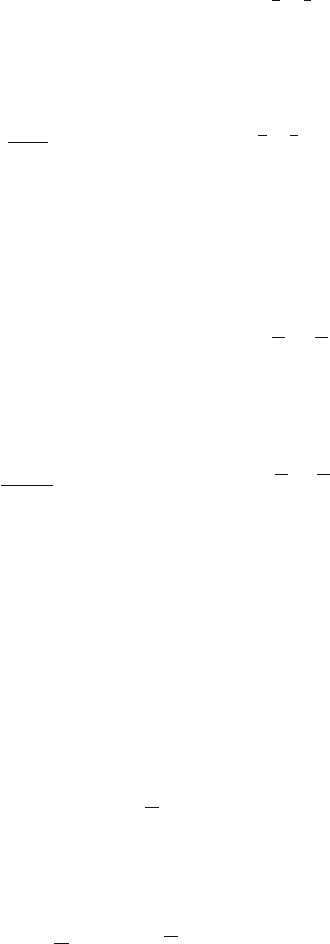
52 2 Foundations and Definitions
As in the one-dimensional case, one can consider periodic functions
f
p
(
x +X,y +Y
)
= f
p
(
x,y
)
. Similarly to (2.3-9) and (2.3-12), the Fourier series
f
p
(
x,y
)
=
m
n
a
m,n
·e
j2π
(
m
X
x+
n
Y
y
)
(2.3-44)
with the Fourier coefficients
a
m,n
=
1
X · Y
+X/2
−X/2
+Y/2
−Y/2
f
p
(
x,y
)
·e
−j2π
(
m
X
x+
n
X
y
)
dxdy (2.3-45)
is obtained.
In connection with the band-limited functions and the sampling theorem (Section
2.5), the periodic spectra with F
p
k
x
+L
x
,k
y
+L
y
= F
p
k
x
,k
y
are of interest.
Generalizing (2.3-38) and (2.3-39), we obtain the following formulae:
F
k
x
,k
y
=
m
n
c
m,n
·e
−j2π
m
L
x
k
x
+
n
L
y
k
y
(2.3-46)
and
c
m,n
=
1
L
x
·L
y
+L
y
/2
−L
x
/2
+L
y
/2
−L
y
/2
F
k
x
,k
y
·e
j2π
m
L
x
k
x
+
n
L
y
k
y
. (2.3-47)
The integrals considered above of type
f
(
t
)
=
F
(
ν
)
·e
j2πν t
dν (2.3-48)
cannot always be represented in closed forms. Often one has to use numerical meth-
ods. For this purpose the Discrete Fourier Transform (DFT) is adequate, because it
can be calculated very fast by the Fast Fourier Transform (FFT) algorithm.
The DFT is defined by the forward transform
f
k
=
N−1
l=0
F
l
·e
j
2π
N
k·l
;(k = 0,...,N −1). (2.3-49)
and the backward transform
F
l
=
1
N
N−1
k=0
f
k
·e
−j
2π
N
k·l
;(l = 0,...,N − 1). (2.3-50)

2.3 Fourier Transforms 53
If the F
l
(l =0,...,N-1) are given, the f
k
can be computed (for arbitrary values of
N) by the simple algorithm
a = 2π/N
for k = 0...N-1 do begin
a
k
= a · k
Re_f
k
= 0
Im_f
k
= 0
for l = 0...N-1 do begin
a
kl
= a
k
· l
sn = sin(a
kl
)
cs = cos(a
kl
)
Re_f
k
= Re_f
k
+[Re_F
l
· cs - Im_F
l
· sn]
Im_f
k
= Im_f
k
+[Re_F
l
· sn + Im_F
l
· cs]
end
end
(similarly for the backward transform). One needs O(N
2
) arithmetical operations. If
N is a power of two then the various algorithms of the FFT [see Wikipedia (2004)]
can be used which need only O(N·logN) operations. For sufficiently large values of
N, DFT calculations become practicable only if the FFT is used.
A simple example shows the possibility of approximating the integral (2.3-48)
by the DFT. Let |F(ν)| be very small or even equal to zero for frequencies outside
the interval –ν
g
≤ ν ≤ +ν
g
. Then
f
(
t
)
≈
+ν
g
−ν
g
F
(
ν
)
·e
j2πν t
dν.
If one approximates this integral by a sum of rectangles with heights F(ν
l
) (ν
l
=
l ·ν-ν
g
,l= 0,...,N–1) and widths ν = 2ν
g
/N, then one obtains
f
(
t
)
≈ ν · e
−j2πν
g
t
·
N−1
l=0
F
(
ν
l
)
·e
j2π l ν t
.
If it is sufficient to compute the function f(t) only at the sampling points t
k
=
k·t–τ (k = 0,...,N–1), these values are given by
f
(
t
k
)
≈ ν · e
−j2πν
g
(
kt−τ
)
·
N−1
l=0
F
(
ν
l
)
·e
−j2π l ν τ
·e
j2πνtkl
.
Finally, if ν·t =1/N (t =
1
/
2
ν
g
) is chosen and the abbreviation G
l
= F
(
ν
l
)
·
e
−j2π l ν τ
and the DFT
g
k
=
N−1
l=0
G
l
·e
j
2π
N
k·l
;(k = 0,...,N −1)
54 2 Foundations and Definitions
are used, the required values f(t
k
) can be calculated according to
f
(
t
k
)
≈ ν ·
(
−1
)
k
·e
j2πν
g
τ
·g
k
. (2.3-51)
The same is true in the two-dimensional case if the 2D-DFT is introduced by
f
k,l
=
N−1
m,n=0
F
m,n
·e
j
2π
N
(
k m+l·n
)
. (2.3-52)
and
F
m,n
=
1
N
2
N−1
k,l=0
f
k,l
·e
−j
2π
N
(
m·k+n·l
)
. (2.3-53)
The precision of this approximation depends strongly on the size of N.Asan
example the values f(t
k
) (2.2-51) are calculated for the spectrum (2.3-24)
F
(
ν
)
= e
−
ν
2
2κ
2
with κ =
1
2π
(
σ = 1
)
.
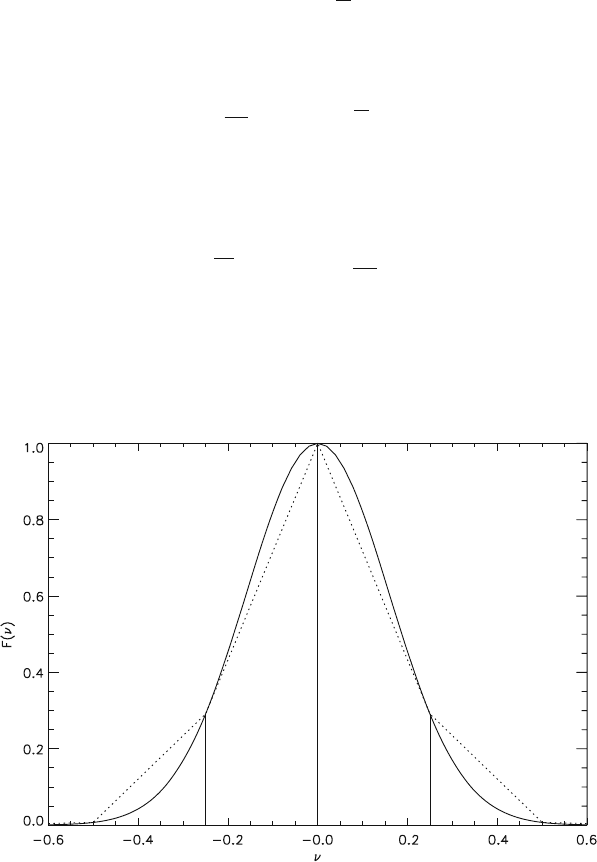
Figure 2.3-8 shows the values F(ν
l
)forN = 8, ν
g
= 1, ν = 0.25 together with
the function F(ν). Figure 2.3-9 shows the values f(t
k
) which have been calculated by
(2.3-51) using the DFT. One can see that these few values are not sufficient for the
Fig. 2.3-8 Samples of spectrum F(ν)(N = 8)

2.3 Fourier Transforms 55
Fig. 2.3-9 Values f(t
k
)forthespectrumofFig.2.3-8(N = 8) calculated with DFT
representation of the function f(t). Better results are obtained with larger values of
N and ν
g
(see Figs. 2.3-10 and 2.3-11 for N = 32).
For practical purposes important examples of Fourier transforms are presented in
Tables 2.3-1, 2.3-2, and 2.3-3.
Some of the results in Table 2.3-3 can be obtained using the formula
N−1
n=0
q
n
=
q
N
−1
q − 1
. (2.3-54)
Fig. 2.3-10 Samples of spectrum F(ν)(N = 32)
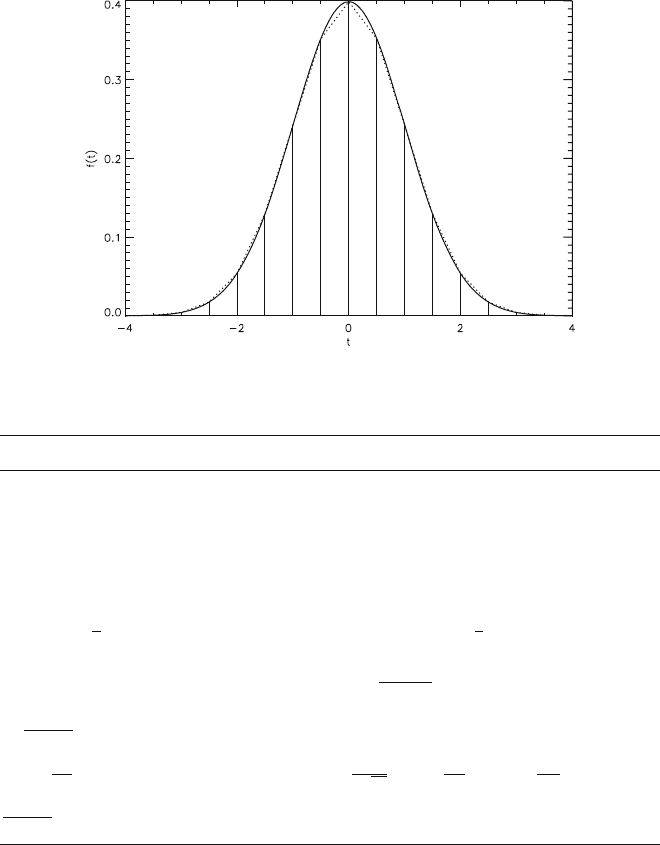
56 2 Foundations and Definitions
Fig. 2.3-11 Values f(t
k
) for the spectrum of Fig. 2.3-10 (N = 32) calculated with DFT
Table 2.3-1 One-dimensional Fourier transform
F(ν) F(t)
Const = 1 δ(t)
δ(ν–ν0) Exp(j2πν0t)
exp(–j2πντ) δ(t–τ )
[δ(ν–ν0) – δ(ν+ν0)]/2j sin(2πν0t)
[δ(ν–ν0) + δ(ν+ν0)]/2 cos(2πν0t)
∞
n=−∞
δ
ν −
n
T
= T ·
∞
n=−∞
exp
(
±j2πNνt
)
∞
n=−∞
exp
±j2πn
t
T
= T ·
∞
n=−∞
δ
(
t −nT
)
1 −ν
g
/2 ≤ ν ≤+ν
g
/2
0elsewhere
ν
g
·
sin
(
πν
g
t
)
πν
g
t
τ ·
sin (πντ)
πντ
1 −τ/2 ≤ t ≤+τ/2
0elsewhere
exp
−
ν
2
2κ
2
1
σ
√
2π
exp
−
t
2
2σ
2
; σ =
1
2πκ
τ
1+j2πντ
exp ( −t/τ ) t ≥ 0
0 t < 0
2.4 Linear Systems
Electronic and optical systems often can be described by so-called linear systems,
which are studied in systems theory. A linear system describes the connection
between an input signal f
in
(x,y,z,...), which can depend on multiple variables, and
an output signal f
out
(x,y,z,...) in such a way that a superimposition
f
in
= a ·f
(
1
)
in
+b ·f
(
2
)
in
(2.4-1)
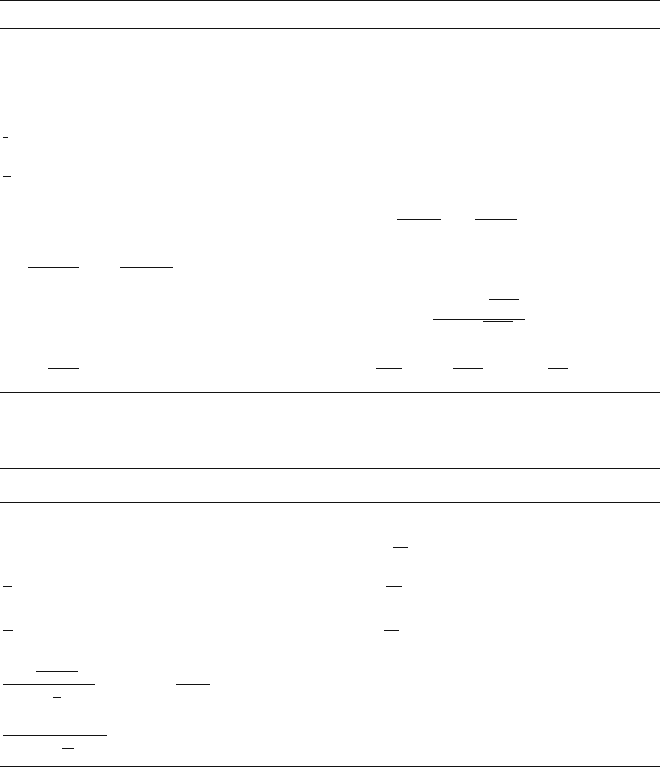
2.4 Linear Systems 57
Table 2.3-2 Two-dimensional Fourier transform
F(k
x
,k
y
) f(x,y)
Const = 1 δ(x)·δ(y)
δ
k
x
−k
0
x
·δ
k
y
−k
0
y
exp
j2π
k
0
x
x +k
0
y
y
exp
−j2π
k
x
x
0
+k
y
y
0
δ
(
x −x
0
)
·δ
(
y −y
0
)
1
2
δ
k
x
−k
0
x
·δ
k
y
−k
0
y
+δ
k
x
+k
0
x
·δ
k
y
+k
0
y
cos
2π
k
0
x
x +k
0
y
y
1
2j
δ
k
x
−k
0
x
·δ
k
y
−k
0
y
−δ
k
x
+k
0
x
·δ
k
y
+k
0
y
sin
2π
k
0
x
x +k
0
y
y
1 − K/2 ≤ k
x
≤+K/2; −L/2 ≤ k
y
≤+L/2
0elsewhere
K ·
sin (πKx)
πKx
·L ·
sin (πLy)
πLy
L
x
·
sin
(
πk
x
L
x
)
πk
x
L
x
·L
y
·
sin
(
πk
y
L
y
)
πk
y
L
y
1 − L
x
/2 ≤ x ≤+L
x
/2; − L
y
≤ y ≤ L
y
/2
0elsewhere
1 k
2
x
+k
2
y
≤ K
2
g
0elsewhere
πK
2
g
·2 ·
J
1
2πK
g
√
x
2
+y
2
2πK
g
√
x
2
+y
2
a
exp
−
k
2
x
+k
2
y
2κ
2
1
2πσ
2
exp
−
x
2
+y
2
2σ
2
; σ =
1
2πκ
a
J1(x) is the Bessel function of first order
Table 2.3-3 One-dimensional DFT
F
l
(0 ≤ l ≤ N–1) f
k
(0 ≤ k ≤ N–1)
Const = 1 N·δk,0
δ
l,n
(0 ≤ n ≤ N −1) exp
j
2π
N
k ·n
N
2
δ
l−n,0
+δ
l+n,0|N
a
cos
2π
N
k ·n
N
2j
δ
l−n,0
−δ
l+n,0|N
a
sin
2π
N
k ·n
sin
π
k
2
−k
1
+1
N
·l
sin
π
1
N
·l
·exp
−jπ
k
1
+k
2
N
·l
1 k
1
≤ k ≤ k
2
0elsewhere
(
0 ≤ k
1
≤ k
2
≤ N −1
)
exp
(
−α·N
)
−1
exp
−α−j
2π
N
·l
−1
exp
(
−α · k
)
a
δ
l+n,0|N
is the abbreviation for δ
l+n,0|N
=
1 l +n = 0orl +n = N
0elsewhere
.
of input signals leads to an analogous superimposition
f
out
= a ·f
(
1
)
out
+b ·f
(
2
)
out
(2.4-2)
of output signals (linearity).
This is not an introduction into systems theory. Only few basics are presented
in order to understand optoelectronic systems. Of special importance are the shift-
invariant linear systems which are defined by the following connection between
58 2 Foundations and Definitions
input and output signals:
f
out
(
x,y,z,t
)
=
h
x −x
,y − y
,z − z
,t −t
·f
in
x
,y
,z
,t
dx
dy
dz
dt
(2.4-3)
Equation (2.4-3) describes a four-dimensional system. Shift-invariance means that a
shift of the input signal (f
in
(x’,y’,z’,t’) → f
in
(x’–a,y’–b,z’–c,t’–d)) leads only to the
same shift of the output signal without any other change.
One- and two-dimensional systems, which describe the transform of electrical
and optical signals, are discussed here. One-dimensional systems are important for
the understanding and design of the analogue-electronic signal processing units
(front-end electronics) of a sensor. Here, the function f(t) is a time-dependent electric
quantity such as current or voltage. One of the important kinds of signal processing
is the filtering of the signal f(t) in order to reduce unwanted signal components such
as disturbances and noise. It is defined by the convolution
f
out
(
t
)
=
+∞
−∞
h
t −t
·f
in
t
dt
, (2.4-4)
i.e. by a linear system of the kind Fehler! Verweisquelle konnte nicht gefunden
werden. One can write this operation symbolically as
f
out
= h ⊗f
in
. (2.4-5)
The reaction of the filter (2.4-4) to a needle-shaped input impulse δ(t) (delta-
function; see Chapter 2 .Chapter 3 ) is considered first. In this case the output signal
f
out
(
t
)
= h
(
t
)
is obtained. Therefore h(t) is called the impulse response. Because
the input signal δ(t) is concentrated at t = 0, there cannot be an output signal for t <
0 because of causality. Therefore
h(t) = 0fort < 0. (2.4-6)
The impulse response of a physical system must always fulfill the condition
(2.4-6). This substantially restricts the possibilities of signal filtering.
Important for the understanding the filtering operation is the representation of
the convolution (2.4-4) in frequency space. Applying the Fourier back-transform
(2.3-6) to (2.4-4), one obtains the connection
F
out
(
ν
)
= H
(
ν
)
·F
in
(
ν
)
, (2.4-7)
which means that in frequency space the filter reduces to the simple multiplica-
tion of the input spectrum with the frequency response H(ν) of the filter. This is a
fundamental advantage for systems analysis and synthesis.
2.4 Linear Systems 59
If the frequency response H(ν) of the filter is written as
H
(
ν
)
=
|
H
(
ν
)
|
·e
j
H
(
ν
)
(2.4-8)
and if F
in
(ν) and F
out
(ν) according to (2.3-5) are represented in the same way, then,
from (2.4-7), the following relationships hold:
|
F
out
(
ν
)
|
=
|
H
(
ν
)
|
·
|
F
in
(
ν
)
|
(2.4-9)
ϕ
out
(
ν
)
=
H
(
ν
)
+ϕ
in
(
ν
)
. (2.4-10)
This means in particular that, if a sinusoidal input signal f
in
(t) =cos(2πνt)is
filtered, the output signal has the same shape and frequency. There occur only an
attenuation and a phase shift: f
out
(t) =|H(ν)|cos(2πνt+
H
(ν)).
Non-sinusoidal functions, however, do not have this advantage: their shape is
changed by filtering. This is the crucial advantage of sinusoidal functions for
systems analysis and design.
Next, some examples are given. The ideal low pass filter has the frequency
response
H
(
ν
)
= A
(
ν
)
·e
−j2πντ
; A
(
ν
)
=
1for−ν
g
≤ ν ≤+ν
g
0 elsewhere
, (2.4-11)
where ν
g
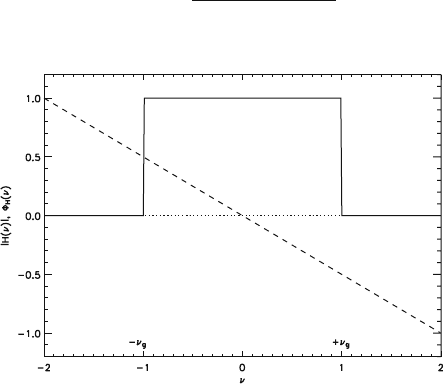
is the cut-off-frequency (see Fig. 2.4-1).
The impulse response of this filter is
h
(
t
)
= 2ν
g
sin
2πν
g
(
t −τ
)
2πν
g
(
t −τ
)
. (2.4-12)
Fig. 2.4-1 Ideal low-pass filter: amplitude and phase response (dashed)forν
g
= 1[Hz],τ =
1/(4π)[s]

60 2 Foundations and Definitions
This function extends to infinity. It does not fulfill the causality condition (2.4-
6)! This means that the ideal low pass filter does not exist in reality: one can only
approximate it. A possibility for such an approximation is the allocation of values
h = 0fort < 0. Evidently, this approximation will become better as the time lag τ .
Figure 2.4-2 shows this.
τ = 0
τ = 5
Fig. 2.4-2 Ideal low-pass filter: impulse response for τ = 0andτ = 5[s]
The so-called low-pass filter of first order (Figs. 2.4-3 and 2.4-4) has the impulse
response
h
(
t
)
=
1
τ
e
−t/τ
for t ≥ 0
0 elsewhere
(2.4-13)
and the frequency response
H
(
ν
)
=
1
1 + j2πντ
;
|
H
(
ν
)
|
=
1
1 +
(
2πντ
)
2
;
H
=−arctan
(
2πντ
)
.
(2.4-14)
τ = 1
τ = 3
Fig. 2.4-3: Low-pass filter of
first order: impulse response
