Русаков В.С. и др. Механика. Методика решения задач
Подождите немного. Документ загружается.

Глава 2. Динамика материальной точки и простейших систем
61
Выражение (2.54) позволяет определить момент времени
0
t ,
в который брусок начинает скользить по доске:
()
α
μ
M
mMmg
t
+
=
0
. (2.55)
Итак:
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=
−
=>
+
==≤
.и:при
,:при
0
0
M
mg
A
m
mgt
att
mM
t
Aatt
μμα
α
(2.56)
Используя полученные выражения для ускорений тел систе-
мы, определим теперь законы изменения скоростей этих тел.
При
0
tt ≤ скорости бруска и доски меняются одинаковым
образом и к моменту времени t будут равны:
()
mM
t
t
mM
t
taV
tt
+
=
+
===
∫∫
2
dd
2
00
αα
υ
. (2.57)
При
0
tt > скорость бруска будет равна
()
=
−
+
+
=
∫
t
t
t
m
mgt
mM
t
0
d
2
2
0
μαα
υ
,
()
(
)
()
0
2
0
22
0
22
ttg
m
tt
mM
t
−−
−
+
+
=
μ
αα
, (2.58)
а скорость доски –
() ()
()
0
2
0
2
0
2
d
2
0
tt
M
mg
mM
t
t
M
mg
mM
t
V
t
t
−+
+
=+
+
=
∫
μαμα
. (2.59)
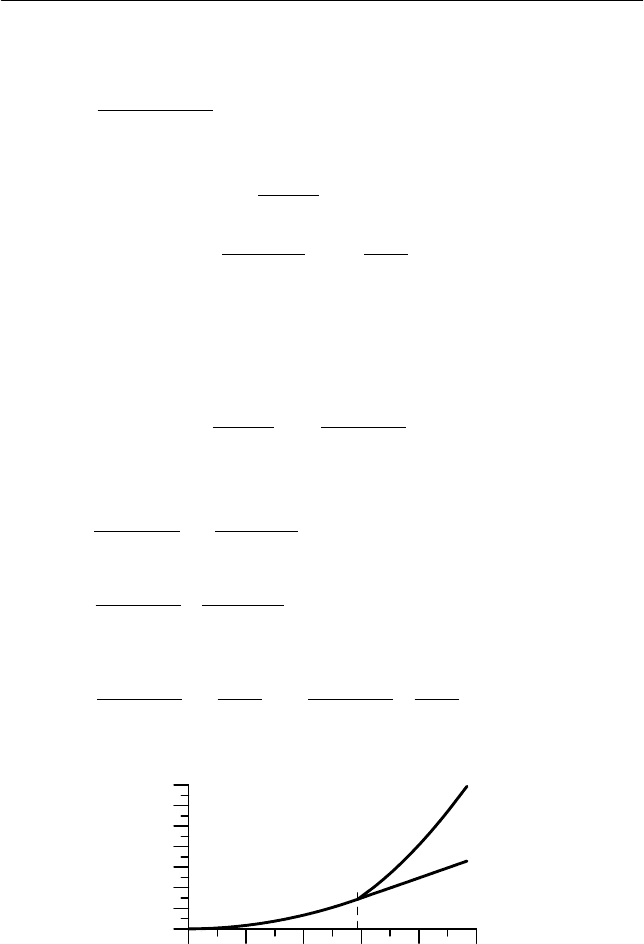
Рис. 2.8
t
t
0
V
0
υ
,V
υ
,V
υ
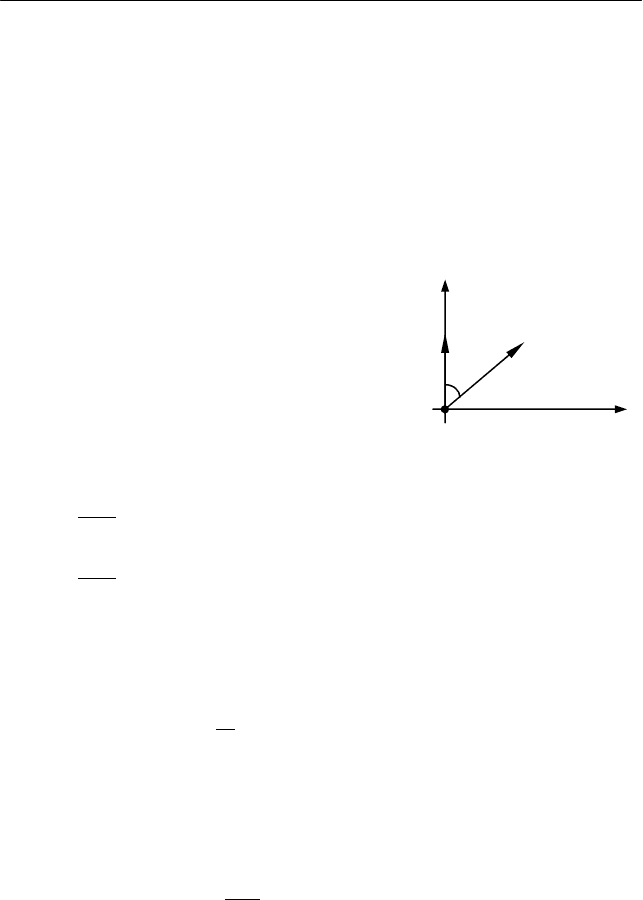
МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ
62
На рис. 2.8 изображены полученные зависимости скоростей
бруска и доски от времени.
Задача 2.5
(Прямая задача динамики)
Найти закон движения материальной точки, движущейся в
однородном и постоянном силовом поле с начальной скоростью
υ
0
,
направленной под произвольным углом
α
к силе F.
Решение
I. Выберем систему координат так,
как показано на рис. 2.9, при этом начало
системы координат совпадает с положе-
нием материальной точки в начальный
момент времени.
II. Запишем уравнения движения
материальной точки в проекциях на оси
выбранной системы координат:
0
d
d
=
t
m
x
υ
, (2.60)
F
t
m
y
=
d
d
υ
. (2.61)
III. Проинтегрируем уравнения (2.60) и (2.61), используя на-
чальные значения скорости
α
υ
υ
sin)(0
0
=
x
и
α
υ
υ
cos(0)
0
=
y
:
α
υ
υ
sin)(
0
=t
x
, (2.62)
t
m
F
t
y
+=
αυυ
cos)(
0
. (2.63)
Интегрируя уравнения (2.62) и (2.63) с учетом начальных
значений координат x
0
= 0 и y
0
= 0, получаем закон движения мате-
риальной точки в координатной форме:
ttx ⋅=
α
υ
sin)(
0
, (2.64)
m
Ft
tty
2
cos)(
2
0
+⋅=
αυ
. (2.65)
Исключив время из уравнений (2.64) и (2.65), получим урав-
нение траектории материальной точки – уравнение параболы:
Рис. 2.9
X
O
Y
F
υ
0
α

Глава 2. Динамика материальной точки и простейших систем
63
xx
m
F
y ⋅+=
α
αυ
ctg
)sin(2
2
2
0
(2.66)
Таким образом, в однородном силовом поле материальная
точка движется по параболе.
Задача 2.6
Тело небольших размеров движется по поверхности непод-
вижного клина с углом при основании
α
. В начальный момент
времени скорость тела равнялась
0
υ и составляла угол
ϕ
0
с ребром
клина (см. рис. 2.10).
Коэффициент трения тела о поверхность клина
α
μ
tg= .
Найти установившуюся скорость скольжения тела.
Решение
I. Выберем систему координат так, как показано на рис. 2.11
(вид сбоку) и рис. 2.12 (вид сверху на поверхность клина). Ось X
направим вдоль наклонной плоскости параллельно ребру клина
(рис. 2.12). При этом ось Y направим по наклонной плоскости пер-
пендикулярно ребру клина, а ось Z перпендикулярно наклонной
поверхности клина (рис. 2.11).
α
ϕ
0
υ
0
Рис. 2.10
Рис. 2.11 Рис. 2.12
Z
Y
mg
N
F
тр
mgsin
α
ϕ
(t)
F
тр
υ
(t)
Y
X
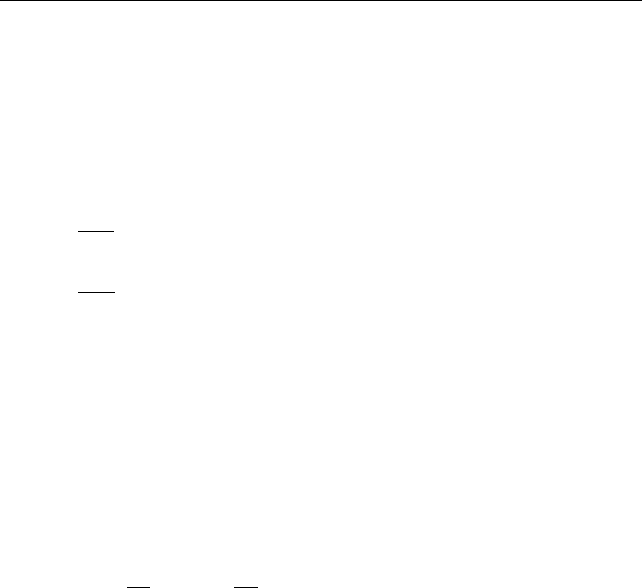
МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ
64
На рис. 2.11 и 2.12 изображены также силы, действующие на
тело в процессе движения: сила тяжести m
g, сила нормальной ре-
акции опоры
N и сила трения скольжения F
тр
.
Скорость тела
υ
(t) составляет с осью X угол φ(t) (см.
рис. 2.12), который является функцией времени.
II. Запишем уравнение движения тела в проекциях на вы-
бранные оси системы координат:
ϕ
υ
cos
d
d
тр
F
t
m
x
−=
, (2.67)
ϕα
υ
sinsin
d
d
тр
Fmg
t
m
y
−= , (2.68)
α
cos0 mgN +
−
= . (2.69)
Используем закон Амонтона – Кулона (см. п. 2.1.2.В) для си-
лы трения скольжения и учтем заданную в условии задачи связь
коэффициента трения
μ
с углом
α
при основании наклонной
плоскости:
NNF ⋅=
=
α
μ
tg
тр
. (2.70)
Запишем тригонометрические функции угла φ, выразив их
через проекции скорости тела:
υ
υ
ϕ
x
=cos ,
υ
υ
ϕ
y
=sin . (2.71)
III. Получена полная система уравнений (2.67) – (2.71) для
определения проекций скорости тела на оси выбранной системы
координат, решить которую в общем виде достаточно сложно из-за
наличия в ней двух связанных нелинейных дифференциальных
уравнений. Однако нет необходимости находить закон изменения
скорости тела. По условию задачи требуется определить устано-
вившуюся скорость тела, т.
е. значение скорости в то время, когда
сумма сил, действующих на тело, станет равной нулю.
Рассмотрим изменение характера движения тела со време-
нем. В плоскости движения на тело действуют две силы: сила тре-
ния скольжения и проекция силы тяжести. Из (2.69) и (2.70) полу-
чим выражение для силы трения:
α
sin
тр
mgF
=
. (2.77)
Как видим, модуль силы трения равен величине проекции силы
тяжести на наклонную плоскость. Действующие на тело силы бу-

Глава 2. Динамика материальной точки и простейших систем
65
дут поворачивать вектор скорости тела до тех пор, пока он не сов-
падет по направлению с осью Y. Следовательно, ускорение обра-
тится в ноль, когда сила трения будет направлена противоположно
составляющей силы тяжести в плоскости движения тела. Дальней-
шее движение будет происходить с постоянной скоростью υ
уст
, на-
правленной вдоль оси Y.
Таким образом, достаточно найти уравнение, связывающее
проекцию скорости тела на ось Y с модулем его скорости. Для это-
го преобразуем полученную систему уравнений (2.67) – (2.71) к
виду:
α
υ
υυ
sin
d
d
g
t
xx
−= , (2.72)
α
υ
υυ
sin1
d
d
g
t
yy
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−= . (2.73)
Производную от модуля скорости по времени представим в виде:
(
)
tttt
yy
xx
yx
d
d
d
d
d
d
d
d
22
υ
υ
υ
υ
υ
υ
υυ
υ
⋅+⋅=+= . (2.74)
Подстановка (2.72) и (2.73) в (2.74) приводит к уравнению:
dt
d
d
d
y
t
υ
υ
−= . (2.75)
Интегрируя (2.75) с учетом начальных условий (
0
)0(
υ
υ
= ,
0
)0(
ϕ
ϕ
=
), получаем:
)sin1(
00
ϕ
υ
υ
υ
++
−
=
y
. (2.76)
Подставляя υ = υ
y
= υ
уст
в (2.76), находим искомый модуль скоро-
сти установившегося движения:
)sin1(
2
0
0
уст
ϕ
υ
υ
+=
. (2.78)
Проанализируем полученное выражение для установившейся
скорости в двух частных случаях.
Если φ
0
= π/2 (начальная скорость тела направлена вниз по
наклонной плоскости), то υ
уст
= υ
0
. Следовательно, движение тела
сразу происходит с постоянной скоростью, поскольку действую-
щие на него силы скомпенсированы.

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ
66
При φ
0
= –π/2 скорость установившегося движения равна
υ
уст
= 0. Начальная скорость, направленная вверх по наклонной
плоскости, приводит к равнозамедленному движению. При этом и
проекция силы тяжести, и сила трения скольжения направлены
противоположно скорости. Через некоторое время скорость тела
обращается в ноль. Сила трения становится силой трения покоя и
меняет направление на противоположное. Движения вниз по на-
клонной плоскости не
происходит, т.к. максимальное значение си-
лы трения покоя в условиях данной задачи совпадает по модулю со
значением проекции силы тяжести на наклонную плоскость.
Задача 2.7
Стальной шарик радиуса r начинает двигаться в сосуде, за-
полненном глицерином, под действием силы тяжести. Найти зави-
симость скорости шарика от времени
υ
(t), а также определить ско-
рость установившегося движения шарика
υ
уст
. Коэффициент вязко-
го трения в глицерине равен
η
, плотность глицерина –
ρ
1
, плот-
ность стали –
ρ
2
. Считать, что сила вязкого трения определяется
формулой Стокса:
в
F =
υη
π
r6.
Решение
I. Выберем систему координат, связанную с сосудом, так, как
показано на рис. 2.13. Начало координат со-
вместим с положением шарика в момент на-
чала его движения. В соответствии с услови-
ем задачи начальная скорость шарика равна
нулю:
(
)
00 =
υ
.
II. Запишем уравнение движения шари-
ка в проекциях на ось X системы координат:
Aв
FFmgma −−
=
, (2.79)
где
в
F – сила вязкого трения, а
A
F – сила
Архимеда.
Используем закон Архимеда и формулу Стокса, описываю-
щие свойства этих сил:
gVF
1A
ρ
=
, (2.80)
υη
π
rF 6
в
=
. (2.81)
Рис. 2.13
X
Y
F
в
F
А
mg
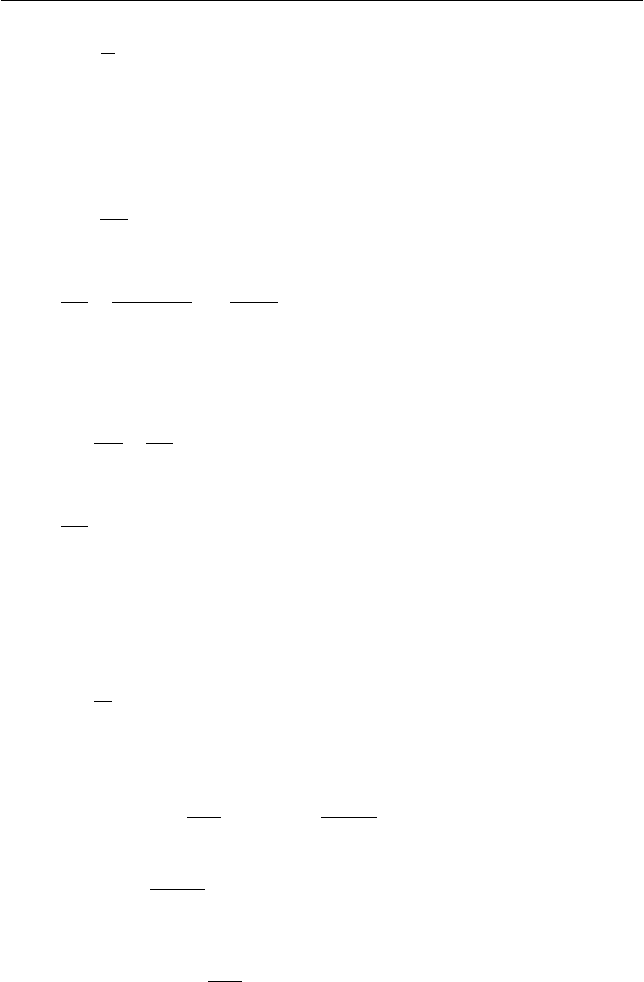
Глава 2. Динамика материальной точки и простейших систем
67
Здесь
3
3
4
rV
π
= – объем шарика.
Выразим также массу шарика через его плотность:
Vm
2
ρ
=
. (2.82)
III. Подставляя (2.80) – (2.82) в уравнение движения (2.79),
получаем:
()
υηπρρ
υ
ρ
rVg
t
V 6
d
d
122
−−= . (2.83)
Для решения уравнения (2.83) приведем его к виду
()
υυ
ρ
ηπ
ρ
ρρυ
BA
V
r
g
t
−=−
−
=
22
12
6
d
d
(2.84)
и сделаем замену переменных:
zBA =
−
υ
. (2.85)
Дифференцируя (2.85) по времени, получаем:
t
z
t
B
d
d
d
d
=−
υ
. (2.86)
С учетом (2.86) выражение (2.84) принимает следующий вид:
Bz
t
z
−=
d
d
. (2.87)
Решим полученное уравнение методом разделения перемен-
ных с учетом начального значения скорости
(
)
00
=
υ
:
Bt
Aez
−
= . (2.88)
Используя формулу (2.85), вернемся к старой переменной
υ
:
()
Bt
e
B
A
−
−= 1
υ
. (2.89)
Подставив значения констант A и B из (2.84), а также значе-
ние V, получим выражение для скорости шарика:
()
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−−−= t
r
r
g
2
2
2
12
2
9
exp1
9
2
ρ
η
η
ρρυ
. (2.90)
При
η
ρ
9
2
2
2
r
t >> скорость движения шарика практически не
изменяется и равна
()
η
ρρυ
9
2
2
12уст
r
g−= . (2.91)

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ
68
Задача 2.8
Брусок скользит по гладкой горизонтальной поверхности со
скоростью
0
υ и по касательной попадает в область, ограниченную
забором в форме полуокружности (рис. 2.14). Определить время,
через которое брусок покинет эту область. Радиус кривизны забора
R, коэффициент трения скольжения бруска о поверхность забора
μ
.
Размеры бруска много меньше R.
Решение
I. Выберем произвольную инер-
циальную систему отсчета, жестко
связанную с забором. Изобразим на
рисунке тангенциальную ось, задан-
ную ортом
τ , направленную вдоль
скорости движения бруска, и нор-
мальную ось, заданную ортом
n
, на-
правленную к центру кривизны тра-
ектории перпендикулярно скорости
(см. теоретический материал в Главе 1).
II. Запишем уравнения движения бруска относительно инер-
циальной системы отсчета, жестко связанной с забором, в проекци-
ях на тангенциальную и нормальную оси:
тр
d
d
F
t
mma −==
υ
τ
, (2.95)
N
R
mma
n
==
2
υ
. (2.96)
Воспользуемся законом Амонтона – Кулона для силы трения
скольжения:
NF
μ
=
тр
. (2.97)
III Из (2.95) – (2.97) получим уравнение для определения мо-
дуля скорости бруска:
Rt
2
d
d
υ
μ
υ
−= . (2.98)
Решая уравнение (2.98) методом разделения переменных, по-
лучим:
t
R
d
d
2
μ
υ
υ
−=
, (2.99)
F
тр
Рис. 2.14
n
υ
0
τ
N
F
тр
υ

Глава 2. Динамика материальной точки и простейших систем
69
Ct
R
+=
μ
υ
1
. (2.100)
Константу С в (2.100) определим из начальных условий
(
0
)0(
υ
υ
= ):
0
1
υ
=C
.
Таким образом, модуль скорости бруска в момент времени t,
когда брусок еще движется вдоль забора, определяется следующим
образом:
t
R
0
0
1
1
μυ
υυ
+
=
. (2.101)
Заметим, что для любого момента времени t и при любой, не
равной нулю, начальной скорости υ
0
, скорость бруска υ > 0. Это
означает, что брусок не остановится, а обязательно пройдет всю
область, ограниченную забором, поскольку с уменьшением скоро-
сти движения бруска уменьшается и сила трения скольжения меж-
ду бруском и забором.
Путь, пройденный телом за время t
d с момента времени t,
при движении вдоль забора, равен:
t
t
R
ts d
1
1
dd
0
0
μυ
υυ
+
==
. (2.102)
Путь, пройденный телом за время
t движения вдоль забора
получим интегрированием (2.102) по времени:
⎟
⎠
⎞
⎜
⎝
⎛
+= t
R
R
s
0
1ln
μυ
μ
. (2.103)
Для определения времени, через которое брусок покинет об-
ласть, ограниченную забором преобразуем (2.103) к виду:
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
1
0
s
R
e
R
t
μ
μυ
. (2.104)
Поскольку длина забора
Rs
π
=
искомое время движения
бруска вдоль забора
0
t равно:
()
1
0
0
−=
πμ
μυ
e
R
t
. (2.105)
МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ
70
При малых значениях коэффициента трения (1
<
<
πμ
) время
движения бруска
0
t будет равно
()
()
000
0
1...)1(1
υ
π
πμ
μυμυ
πμ
RR
e
R
t ≅−++=−=
. (2.106)
Задача 2.9
На столе лежит доска массой
М = 1 кг, а на доске – груз мас-
сой
m = 2 кг. Какую силу
F
нужно приложить к доске, чтобы она
выскользнула из-под груза? Коэффициент трения между грузом и
доской равен
μ
1
= 0,25, а между доской и столом –
μ
2
= 0,5.
Решение
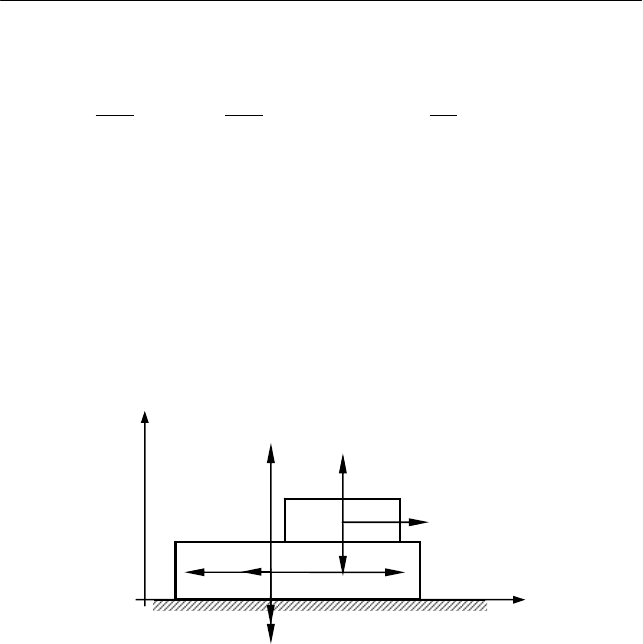
I. Выберем систему координат так, как показано на рис. 2.15
и изобразим силы, действующие на тела системы.
На груз в процессе движения действуют сила тяжести
mg, си-
ла трения
1тр
F и сила нормальной реакции доски N. К доске при-
ложены горизонтальная сила
F, сила тяжести Mg, сила нормальной
реакции стола
R, сила нормального давления груза N и силы трения
со стороны груза и стола
1тр
F и
2тр
F . Силами сопротивления воз-
духа пренебрегаем.
Проанализируем характер движения тел системы. Если при-
ложенная к доске сила
F мала, то груз и доска движутся с одинако-
вым ускорением (или покоятся), а сила трения
1тр
F между грузом и
доской является силой трения покоя. С увеличением внешней силы
Рис. 2.15
X
N
mg
F
тр1
Y
F
тр1
F
F
тр2
R
Mg
N
