Русаков В.С. и др. Механика. Методика решения задач

Глава 1. Кинематика материальной точки и простейших систем

41

Ответ: N

u

N

+

=

′

υ

.

Задача 4

Два трактора, движущиеся со скоростями

1

υ

и

2

υ

, буксируют

с помощью тросов автомобиль (см. рис.).

Определить модуль и направление скорости

υ

автомобиля в

тот момент, когда тросы параллельны векторам

1

υ и

2

υ , а угол ме-

жду ними равен

α

.

Ответ:

α

αυυυυ

υ

sin

cos2

21

2

1

−+

= ,

⎟

⎠

⎞

⎜

⎝

⎛

−+

=

αυυυυ

αυ

β

cos2

sin

arccos

21

2

1

, где

1

β

– угол между век-

торами

υ и

1

υ .

Задача 5

Тело А подвешено на нитях, перекинутых через блоки В и С

малого диаметра так, что АВ = ВС (см. рис.).

Концы нитей тянут с одинаковыми скоростями

υ

. Расстоя-

ние между блоками В и С равно

L. Найти модуль скорости

A

υ

тела

2

υ

1

υ

α

υ

A

B C

L

H

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

42

А в тот момент, когда оно находится на расстоянии H от прямой

ВС.

Ответ:

2

A

2

1

⎟

⎠

⎞

⎜

⎝

⎛

+=

H

L

υυ

.

Задача 6

Лодку подтягивают к пристани высотой

Н с помощью верев-

ки, наматываемой на вал лебедки. Радиус вала равен

R << H. Вал

вращается с постоянной угловой скоростью

ω

. Определить зависи-

мость модулей скорости и ускорения лодки от длины веревки

L > Н. Движение лодки считается поступательным.

Ответ:

22

HL

RL

−

=

ω

υ

,

()

23

22

2

)(

HL

rH

a

−

=

ω

.

Задача 7.

Найти уравнение кинематической

связи для ускорений тел, подвешенных на

нерастяжимых нитях (см. рис.).

Ответ:

02

321

=++ aaa

, где

1

a

,

2

a

и

3

a

–

проекции ускорений тел на вертикальную

ось декартовой системы координат.

Задача 8

Определить закон изменения модуля скорости материальной

точки, движущейся в плоскости, если ее движение описывается в

полярной системе координат следующим законом: )1()(

btatr −

=

,

bt

t

−

=

1

)(

ϕ

, где a и b – положительные постоянные величины.

Ответ:

2

)1(

1

bt

ab

−

+=

υ

, при

b

t

1

< .

3

2

1

Глава 1. Кинематика материальной точки и простейших систем

43

Задача 9

Четыре тела подвешены на нерастя-

жимых нитях (см. рис.). Найти ускорение

тела 4, если известны ускорения остальных

трех тел.

Ответ:

()

42

3214

aaaa

+

+−= , где

1

a ,

2

a ,

3

a и

4

a – проекции ускорений тел на верти-

кальную ось декартовой системы координат.

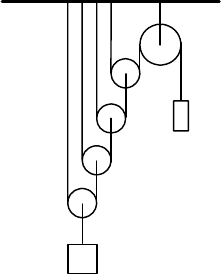
Задача 10

Найти уравнение кинематической связи для ускорений тел,

подвешенных на нерастяжимых нитях так, как показано на рисун-

ке.

Ответ:

0

2

1

2

1

2

54321

=

⎟

⎠

⎞

⎜

⎝

⎛

+++

+

+ aaa

R

r

a

R

rR

a

,

где

1

a ,

2

a ,

3

a ,

4

a и

5

a – проекции ускорений тел на вертикальную

ось декартовой системы координат.

4

3

1 2

1

2

3

r

R

4

5

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

44

Задача 11

Два тела подвешены на нерастя-

жимых нитях, как показано на рисунке.

Определить ускорение тела 2, если из-

вестно ускорение тела 1.

Ответ:

12

16aa −= , где

1

a и

2

a – про-

екции ускорений тел на вертикальную

ось декартовой системы координат.

2

1

Глава 2. Динамика материальной точки и простейших систем

45

ГЛАВА 2

ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ И

ПРОСТЕЙШИХ СИСТЕМ

2.1. Теоретический материал

2.1.1. Законы Ньютона

Первый закон Ньютона. Существуют такие системы отсче-

та, относительно которых изолированная материальная точка (на

которую не действуют силы) движется равномерно и прямолиней-

но или покоится. Такие системы отсчета называются инерциаль-

ными.

Второй закон Ньютона. В инерциальной системе

отсчета

произведение массы материальной точки на ее ускорение равно

сумме всех сил, действующих на эту материальную точку со сто-

роны других тел:

∑

=

i

m Fa . (2.1)

Третий закон Ньютона. Силы взаимодействия двух матери-

альных точек:

1) парные и приложены к разным материальным точкам,

2) одной природы,

3) равны по модулю,

4) противоположны по направлению,

5) направлены вдоль прямой, соединяющей материальные

точки.

Уравнение движения – второй закон Ньютона, записанный в

векторной форме или в проекциях на оси инерциальной системы

отсчета:

∑

=

i

m Fa или

⎪

⎩

⎪

⎨

⎧

=

∑

i

izz

i

iyy

i

ixx

Fma

.

,

(2.2)

Заметим, что уравнение движения можно записать в проек-

циях на любую

, в том числе и произвольно движущуюся относи-

тельно инерциальной системы отсчета, ось. Для этого достаточно

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

46

умножить скалярно левую и правую части векторного уравнения

движения (2) на единичный вектор (орт), задающий направление

этой оси. Например, на направление скорости

τ

и на направление,

перпендикулярное скорости

n :

,

∑

=

i

inn

Fma

ττ

(2.3)

где

)()()( ttat

nn

na

=

и

)()()( ttat τa

ττ

=

– нормальная и тангенци-

альная составляющие ускорения материальной точки.

Законы динамики – это законы Ньютона и законы, описы-

вающие индивидуальные свойства сил.

2.1.2. Законы, описывающие индивидуальные свойства сил

А. Гравитационные силы

Закон всемирного тяготения.

Материальные точки притя-

гиваются друг к другу с силами

21

F и

12

F (см. рис. 2.1), модули

которых пропорциональны произведению их масс и обратно про-

порциональны квадрату расстояния между ними:

12

3

12

21

1221

rFF

r

mm

G=−= . (2.4)

Здесь

G = 6,673⋅10

−11

Н⋅м

2

/кг

2

– гравитационная постоянная,

1212

rrr −= .

Силы гравитационного взаимодействия сферически симмет-

ричных тел, как нетрудно показать, определяются выражением

Рис. 2.1. Ориентация сил гравитационного взаимодействия

дв

у

х мате

р

иальных точек

m

1

r

S

m

2

r

12

r

21

F

12

F

Глава 2. Динамика материальной точки и простейших систем

47

(2.4), в котором

12

r – радиус-вектор центра второго тела относи-

тельно центра первого тела.

Сила тяжести, действующая на материальную точку, –

сумма силы гравитационного притяжения Земли (или любого дру-

гого космического объекта) и центробежной силы инерции (см.

Главу 4), действующей на материальную точку в системе отсчета,

связанной с Землей.

Сила тяжести, действующая на тело, – сумма сил тяжести,

действующих на материальные точки этого тела.

В однородном поле силы тяжести вблизи поверхности Земли

сила тяжести

т

F равна произведению массы тела m на ускорение

центра масс тела при свободном падении (

ускорение свободного

падения

)

g

относительно Земли: gF m

=

т

.

Вес тела – сила, с которой тело, находящееся в поле сил тя-

жести, действует на неподвижную относительно него опору или

подвес, препятствующие свободному падению тела.

Б. Упругие силы

Если после прекращения внешнего воздействия деформиро-

ванное тело восстанавливает свою форму и размеры, то деформа-

ция называется упругой.

Закон Гука. При малых упругих деформациях величина де-

формации пропорциональна величине вызывающей ее силы.

В частности, при деформации растяжения (сжатия) упругого

стержня (пружины, резинового шнура) деформация стержня про-

порциональна величине вызывающей ее силы, действующей вдоль

стержня:

F

k

l

1

Δ = . (2.5)

Здесь k –

коэффициент жесткости (упругости) стержня,

0

Δ lll −=

– удлинение стержня, l и l

0

– длина стержня в деформированном и

недеформированном состояниях (см. рис. 2.2).

Если сила, действующая на стержень, направлена противопо-

ложно указанному на рис. 2 направлению, то упругий стержень ис-

пытывает сжатие. При этом

0Δ

<

l и F в формуле (2.5) следует счи-

тать проекцией силы

F

на ось X системы координат, изображен-

ной на рис. 2.2.

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

48

При деформации растяжения (сжатия) однородного упругого

стержня с постоянным вдоль стержня сечением относительное уд-

линение стержня

ε

пропорционально нормальному напряжению

σ

:

σε

E

1

=

. (2.6)

Здесь E –

модуль Юнга материала, из которого сделан стержень,

0

Δ

l

=

ε

– относительное удлинение стержня,

S

F

=

σ

– нормальное

напряжение

, S – площадь поперечного сечения стержня.

Заметим, что для однородного упругого стержня с постоян-

ным вдоль стержня сечением коэффициент жесткости (упругости)

этого стержня связан с модулем Юнга соотношением:

E

L

S

k =

. (2.7)

В случае растяжения (сжатия) стержня уменьшаются (увели-

чиваются) его поперечные размеры. При этом отношение относи-

тельного поперечного сжатия стержня к его относительному удли-

нению зависит только от материала стержня и называется коэффи-

циентом Пуассона:

ε

μ

⊥

−= . (2.8)

Здесь

μ

– коэффициент Пуассона,

00

0

Δ

d

dd

=

−

=

⊥

ε

– относитель-

ное изменение поперечных размеров стержня, d и d

0

– поперечный

линейный размер стержня в деформированном и недеформирован-

ном состояниях (см. рис. 2.2).

Рис. 2.2. Удлинение стержня под действием

продольной силы

l

0

F

l

d

0

d

X

Y

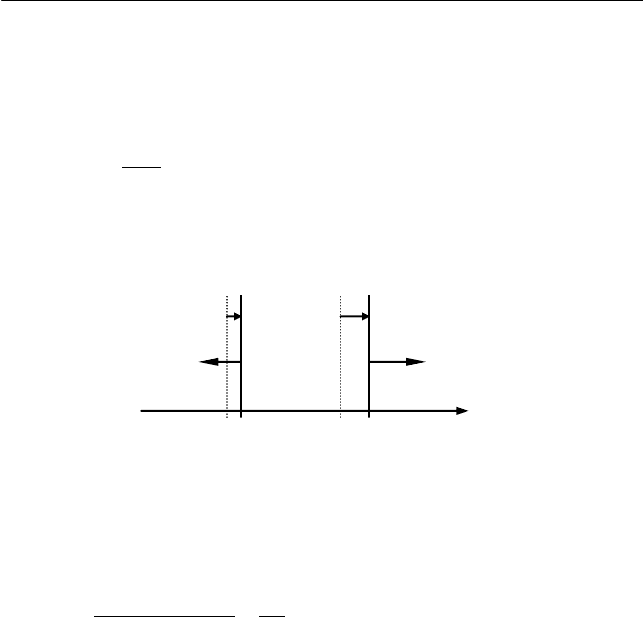
Глава 2. Динамика материальной точки и простейших систем

49

При деформации стержня возникают внутренние упругие си-

лы

упр

F , действующие между его частями, которые стремятся вер-

нуть стержень в недеформированное состояние. Напряжение упру-

гих сил равно

S

F

упр

=

σ

. (2.9)

Рассмотрим слой стержня с координатами границ

x

и

xx d+

вдоль стержня (см. рис. 2.3).

В результате действия внутренних упругих сил возникает

смещение левой

ξ

(x) и правой

ξ

(x+dx) границ выделенного слоя.

Тогда

относительная продольная деформация

ε

этого слоя равна

'

d

)()d(

x

xx

xxx

ξ

ξξξ

ε

=

∂

=

−+

= . (2.10)

Закон Гука в этом случае принимает вид

'

упр

)(

x

EEx

ξεσ

== . (2.11)

В случае деформации слоя изменяются его поперечные раз-

меры. При этом отношение поперечной к продольной деформации

определяется коэффициентом Пуассона в соответствии с (2.8).

При ускоренном движении стержня под действием внешней

силы, вызывающей его деформацию, возникают неоднородные

вдоль стержня напряжения упругих сил. В этом случае возникаю-

щие неоднородные деформации по-прежнему определяются

выра-

жениями (2.11), (2.8).

Рис. 2.3. Смещение границ выделенного

слоя сте

р

жня

x x+dx

ξ

(x+dx)

ξ

(x)

σ

(x)

σ

(x+dx)

X

МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ

50

В. Силы трения

Сила трения

– составляющая силы непосредственного взаи-

модействия тел при соприкосновении вдоль плоскости соприкос-

новения.

Сила нормального давления (реакции опоры) – состав-

ляющая силы взаимодействия тел при непосредственном сопри-

косновении вдоль направления нормали к плоскости соприкосно-

вения.

Силы вязкого (внутреннего) трения

в

F – силы трения, воз-

никающие при движении тела в вязкой (жидкой или газообразной)

среде.

При малой величине скорости

υ движения тела относительно

среды

υF

η

−

=

в

, (2.12)

где

η

– коэффициент вязкого (внутреннего) трения.

Сила вязкого трения покоя равна нулю: 0

вп

=

F .

Силы сухого трения

c

F – силы трения, возникающие при

непосредственном соприкосновении твердых тел.

Силы трения покоя

п

F

– силы сухого трения, возникающие

в отсутствие относительного движения взаимодействующих тел.

Сила трения скольжения

cк

F – сила сухого трения, возни-

кающая при относительном движении взаимодействующих тел.

Закон Амонтона – Кулона – эмпирический закон, описы-

вающий свойства сил сухого трения:

1) модуль силы сухого трения покоя может принимать значе-

ния от нуля до некоторого своего максимального значения:

maxп

0 FF ≤≤ ;

2) модуль силы сухого трения скольжения равен максималь-

ному значению модуля силы сухого трения покоя:

maxcк

FF

=

;

3) модуль силы сухого трения скольжения пропорционален

модулю силы нормального давления:

NF

μ

=

cк

, (2.13)

где

μ

– коэффициент (силы сухого) трения, не зависящий от силы

нормального давления, а только от вещества и состояния поверхно-

стей трущихся тел;

Русаков В.С. и др. Механика. Методика решения задач

Подождите немного. Документ загружается.