Румянцев Н.В., Медведева М.И., Полшков Ю.Н., Пелашенко А.В. Практикум по решению задач курса Высшая математика
Подождите немного. Документ загружается.

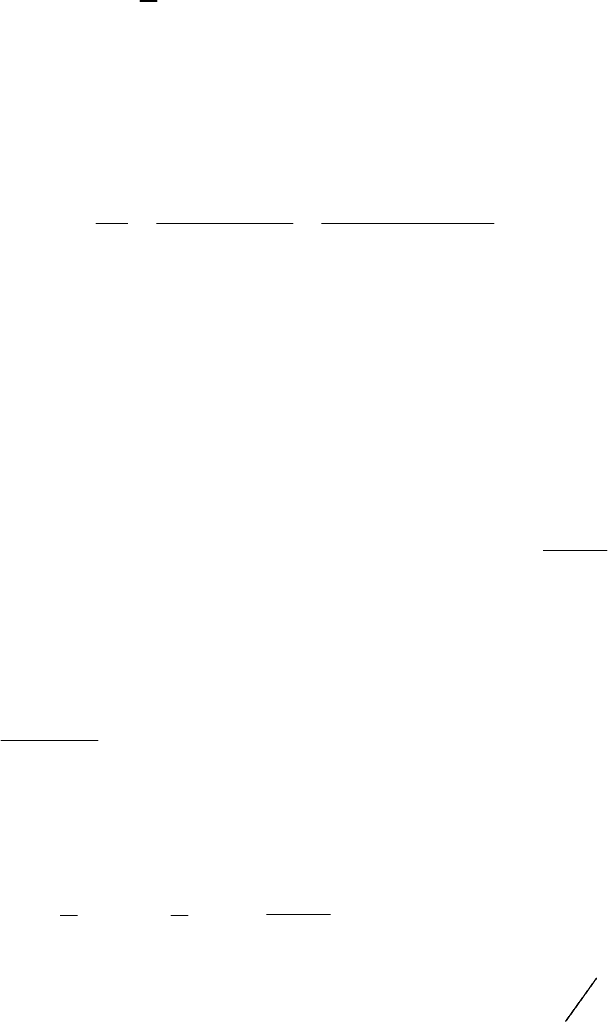
существует для всех
0
x
≠
. Тогда
0
x
=
– критическая то ри переходе через
точку
0
чка. П
x
=
производная меняет знак «+» на «−», но максимума здесь нет, т.к. в
той точке нарушается непрерывность функции.
Прим ти наибольшее и наименьшее зн е функции
э
ер 4.24. Най ачени
2
3
23 ln
2
yx x x=+−−
на отр
ция определена для
езке [0,5;1] .
Решение. Данная функ
0
x
>
и имеет производную в
каждой точке этого множества. Так как
2
3 4 4 3 (2 1)(2 3)
22
22 2
xx x x
yx
xx x
+
−−
′
=+− = =
+
,
то и – критические точки. При этом
1
0,5x =
2
1, 5x =−
2
[0,5; 1]x
∉
. Находим зна-
чения а и в критической точке
x =
, (
исходной функции на концах заданного отрезк
1
5
.
0,
(0,5) 1,75 1,5ln2y =− + 1) 0y
=
.
ак как , то и .
Пример 4.25. Найти наименьшее ачение функции
(0,5) 0y <
(0,5) 1,75 1,5ln2
наим
y у==−+
(0) 0
наиб
y у==
Т
зн
2
1
x
y
x
=
+
на проме-
жутке
.
Решение
[1; )
−+∞
. Для всех
1
x
>−
данная функция дифференцируема и ее произ-
водна я
()
2
1
x
−
2
2
1
y
x
′
=
.
=−
и
1
+
Критические точки
1
x
2
x1
=
. Так как
11
(1) )=, (1
22
yy−=−
и
2
lim 0
1
x
x
x
→∞
=
+
,
то наименьшее зн ие функции а интервале
ачен н [1; )
−
+∞
1
2
наим
y =− .
и 4.2 айти промежутки выпуклости и вогнутости функции
4
.
ение. Данная функци дифференцируема на всей числовой прямой.
Найдем вторую производную:
6 , 30 6yxx x
′′′
=− =−
.
Пр мер 6. Н
32
53yx x=−+
Реш я
2
15 y
61

Отсюд
00,=⇔
а
2=
. Так как
yx
′′
0y
′
′
<
, если
0,2
x
<
и , если
0y
′′
>
0,2
x
>
сслед ая функция выпукла при , то и уем
0,2
x
<
и вогнута при
0,2
x
>
.
При э точка
2
том
0,
– точка перегиба.
вых:
x
=
Пример 4.27. Найти асимптоты кри
2
1
x
y
x
2
2
2
1
x
y
x
=
+
1)
=
−
; 2) .
меет вертикальную асимптотуРешение. 1) Кривая и
1
x
=
, так как
22
10 10
li mm ; li
11
xx
→− →+xx
xx
=
−∞ = +∞
(точка
−−
1
x
= является точкой разрыва второго рода).
х наклонные асимптоты:
На одим
2
lim lim 1
(1)
xx
yx
k
x
xx
→∞ →∞
== =
−
,
2
lim( ) lim lim 1
11
x→∞ →∞x x
xx
bykx x
xx
→∞
⎞
⎛⎞
=−= −= =
⎜⎟
⎜⎟
−−
⎝⎠
⎝⎠
.
– наклонная асимптота.
ль ую асимптоту
⎛
Итак, прямая 1yx=+
2) Кривая имеет горизонта н 2
y
=
, так как
2
2x
2
lim 2
1
x
x
→∞
=
+
.
имер 4.28 дование функции
3
2
1
x
y
x
=
−
Пр . Провести полное иссле и по-
строи график
ия функции )
ть ее .
Решение.
1)
Область определен (;1)(1;1)(1;
x
∈
−∞ − − + ∞∪∪ .
точки пересечения с осями координат. Если
2)
Находим
0
x
=
, то 0y
=
,
т.е. график функции пересекает оси координат в точке
(0;0).
3)
Так как
33
22
()
() ()x
,
() 1 1
xx
y yx
xx
−
−= =− =−
−− −
то фу етная и ее график симметричен относительно начала координат
и дост функцию в промежутке
нкция неч
аточно исследовать [0; )
+
∞ .
не ется периодической. Функция явля
62
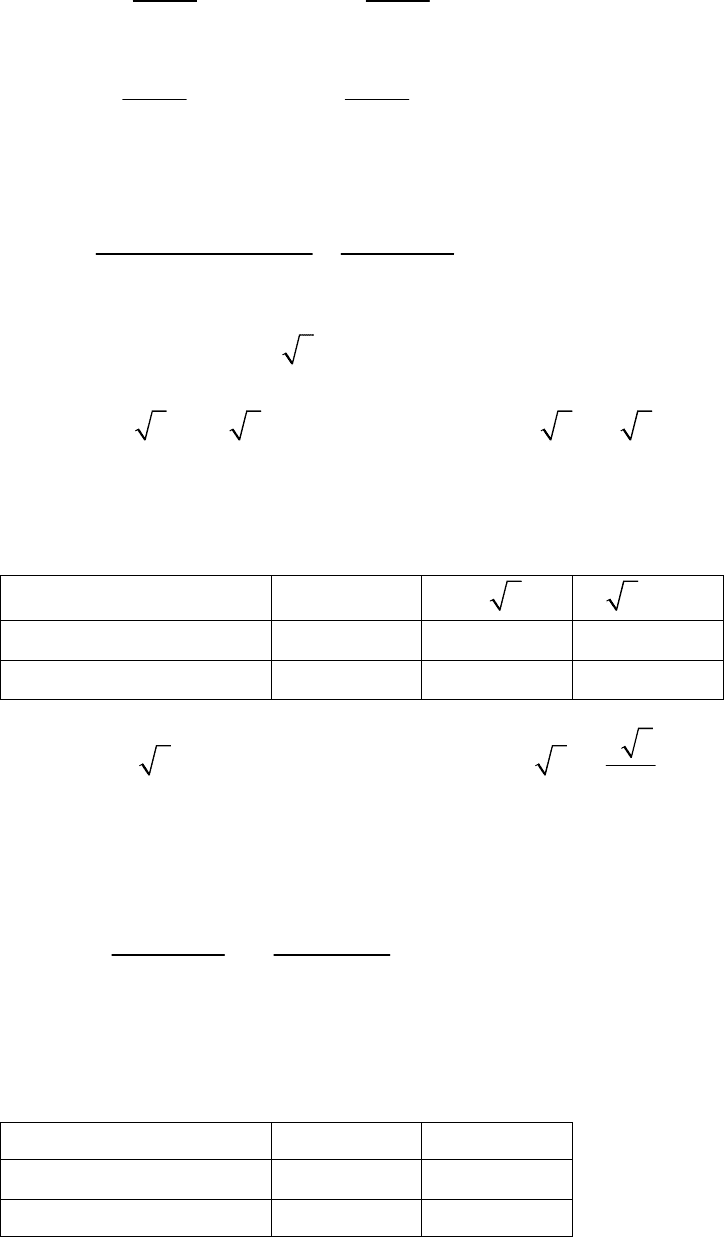
4) Исследуемая
функция непрерывна в области допустимых значений.
Точки
1
x
=
и
1
x
=
точками разрыва. Исследуем характер точек раз-
рыва.
−
являются
33
22
10 10
lim ; lim
11
xx
xx
→− − →− +
==−∞ ==+∞
−−
;
xx
3
lim ;
x
3
22
10 10
lim
11
xx
x
xx
→− →+
== ==∞
−−
.
5) Исследуем функцию на монотонность. Находим точки экстремума:
−∞ +
() ()
22 2
3( 1)2xx x−−
3 2
2
2
( 3)
1
x xx
y
x
⋅ −
′
==
−
.
2
2
1x
−
Тогда
00yx
′
=⇔=
и 3x
=
± и в
1
x
точках
=
±
производная не сущест-
вует. Разбиваем функции на интервалы знакопостоянства
произ
область определения
водной:
(( ; 3 ) 3; ) ( )−−∞ − −∪∪1 1; 0 (0;1) (1; 3 ) ( 3; )− +∞∪∪∪
. Опреде-
ляем знаки , при этом, как было сказано выше,
рассм в
производной в этих интервалах
атри аем только промежуток )[0;
+
∞ . Результаты для удобства записыва-
ем в таблицу
Интервалы
(0;1)
(1; 3 )
(3; )+∞
Знак
()yx
′
− −
+
Монотонность ()yx
убыв ает убывает возрастает
()
min
33
32
2
yy==≈3xТогда точка = – точка минимума и
,6
.
и интервалы выпуклости, вогнуто-
сти. В ункции авна
6)
Находим точки перегиба функции
торая производная исследуемой ф р
() ()
22 2
(3)2(3)xx xx
′
⎡⎤
23
22
11
xx
y
−+
⎢⎥
′′
==
⎢⎥
−−
она обращается
⎣⎦
,
в ноль в точке 0
x
=
и в бесконечность при 1
x
=± . Определяем
знак второй производной, результат записываем в таблицу:
Интервалы
((0;1) 1; )
+
∞
Знак
()yx
′
′
−
+
()yx
выпукла вогнута
7) Находим асимптоты графика.
63
Вертикальные асимптоты
1
x
=
−
и
1
x
=
(
Наклонная асимптота:
см. п. 4).
()
3
1
2
lim lim
1
xx
yx
k
x
x
x
→∞ →∞
==
−
=,
3
22
lim( ) lim lim 0
11
xx
x
→∞ →∞
−
x
bykx x
x
→∞
⎛⎞
=−= −= =
⎜⎟
⎜⎟
−
⎝⎠
xx
⎛⎞
⎝⎠
.
Итак, прямая является наклонной асимптотой.
й функции для
yx=
[0; )
x
∈
+∞
8)
Строим график исследуемо и отображаем
симметрично относительно начала координат (см. рис 4.2.).
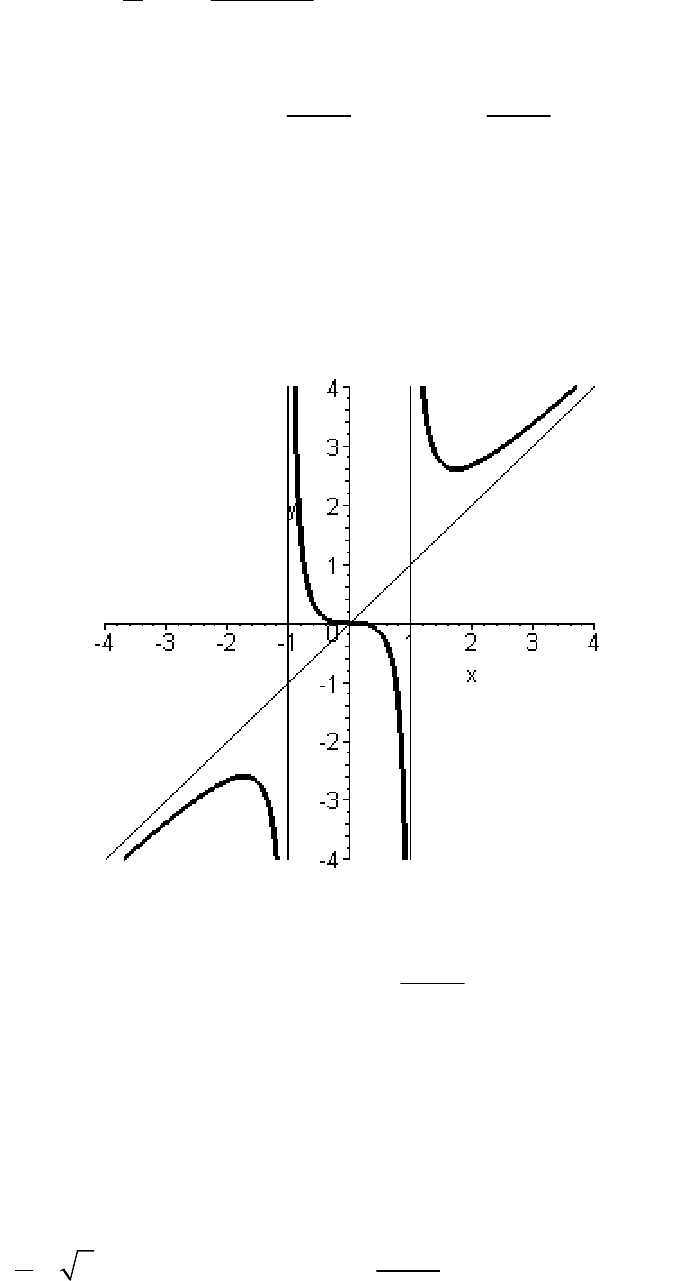
Рис 4.2. График функции
3
2
1
x
y
x
=
−
с асимптотами
Задания для самостоятельного решения
4.29. промежутки возрастания и убывания функции:
1)
15yx x−+
; ;
3)
Найти
2
2)
32
8yx x=−28=
2
x
yxe=
; 4) lnyxx
=
;
5)
2
2
1x
y
x
−
= ;
3
3
x
=yx−
; 6)
64

(
)
3
1yx x
23
x
x
ye e
−
=+
7) =−; 8) ;
9)
;
3
8yx x=−
10)
1
1
yx
x
=+
−
;
11)
x x
; 12)
2
12
1
x
xx
+
−
2
lny=
;
13)
1
5
x
y
=
2
x
y= xe
−
; 14) ;
15)
2
ln
x
x
yx
=
y
x
=
; 16) ;
17)
x x−
; 18)
2
(1)yx x1
=
+−
22
lny=
.
4.30 айти экстремумы функции:
1)
. Н
4
2
4
x
yx−
; 2)
=
ln
x
y
x
= ;
3)
x
yxe
−
=
; 4)
2
(1 )yx x
=
−
;
5)
318yx x x+−+
; 6)
)
32 2
(2)(4yx x
=
−+2= 2
;
7)
2
2
1
yx
x
=+
5yx x=+ −
; 8) ;
)
2
1
yx ; 10)
3
(2 1)
x
yxe=−
;
12)
9
x
=+
4
3
11)
3
3yx x=−
;
4
x
yx
=
+
;
2
2
4
x
13)
y
x
=
−
; 14)
3
(1)xyx
=
−
;
15)
2
3
(1 )yx x=−
; 16)
2
1
x
y
x
=
+
;
17)
2
e
x
y
−
=
; 18)
e
x
y
x
=
.
4.31. Найти экстремум функции
t
yt t t
⎧
− − +
⎪
53
32
5205,
(2 2).
43185,
xt t t=
−
<<
⎨
=−−−
⎪
⎩
4.32. Найти максимумы и минимумы функций:
1)
2
4
4
x
y
x
=
+
; 2)
32
3
2336xx x4
+
−+
;
; 4)
3) sin
yx x=
2
x
yxe
−
=
.
65
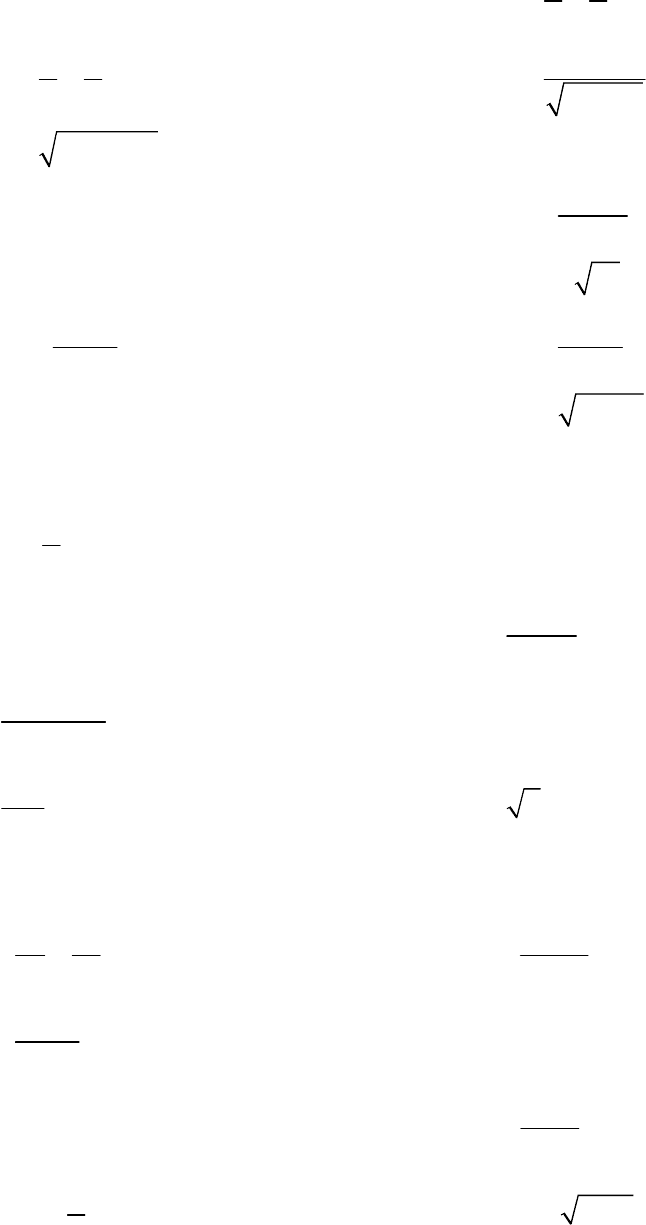
4.33. Найти наибольшее и наименьшее значения функции на за-
данном промежутке, если:
1)
; 2) ;
3)
;
()yfx=
32
() 3 3 2, [2;2]fx x x x x=− ++ ∈−
42
() 8 9, [1;3]fx x x x=− − ∈−
43
() 3 4 1, [2;1]fx x x x=++ ∈−
4)
2
, [1;6]
x+ ∈
;
()
8
x
fx
x
=
5)
3
() , [5; 1]
3
x
fx x
x
=+ ∈−−
; 6)
2
4
() , [3;3]
16
fx x
x
=∈
+
−
;
7)
() (10 ), [0;10]fx x x x=−∈; ; 8)
3
() , [0;4]fx x x x=− ∈
9) ( ) 2ln , [1; ]
f
xx xx e=− ∈ ; 10)
2
() , [4;0]
4
x
fx x
x
=∈−
+
;
2
3
() , [1; )fx x x x
=
−− ∈+∞
11) ( ) ln , (0; )
f
xxxx=− ∈+∞; )12 ;
13)
2
() , [5;0)
1
x
fx x
x
−
=∈−
+
; 14)
2
1
()
1
fx
x
=
+
, ( ; )
x
∈−∞+∞;
15) ( ) ln ln 5, (1;5]
f
xxxx x=− ∈; 16)
2
() 4
f
xx
=
−
,
]
.
4 Найти интервалы выпуклости и вогнутости и точки перегиба сле-
дующих функций:
1
[
1;1−
.34.
)
1
yx
x
=+; 2)
2
(1 2 )
x
yx=+ e
;
3)
; 4
32
32yx x=−
)
2
2
1
x
x
y
x
+
=
+
;
5)
2
1
1
x
y
x
x
+
=
++
; 6 ;
7)
)
2
lnyx x=
ln
x
y
x
= ; 8)
3
(1 )yxx
=
+
;
9)
1
e
x
yx
−
=
; 10)
3
3.yx x
=
−
;
11)
43
43
x
x
y =+
; 12)
2
9x
y
x
−
= ;
13)
2
1
x
y
x
=
+
; 14)
2
e
x
y
−
=
;
15)
4
; 16)
53 2
530yx x x=− + −
5
4
x
y
x
−
=
+
;
17)
2
1
yx
x
=−; 18)
3
43yx
=
−+
;
66
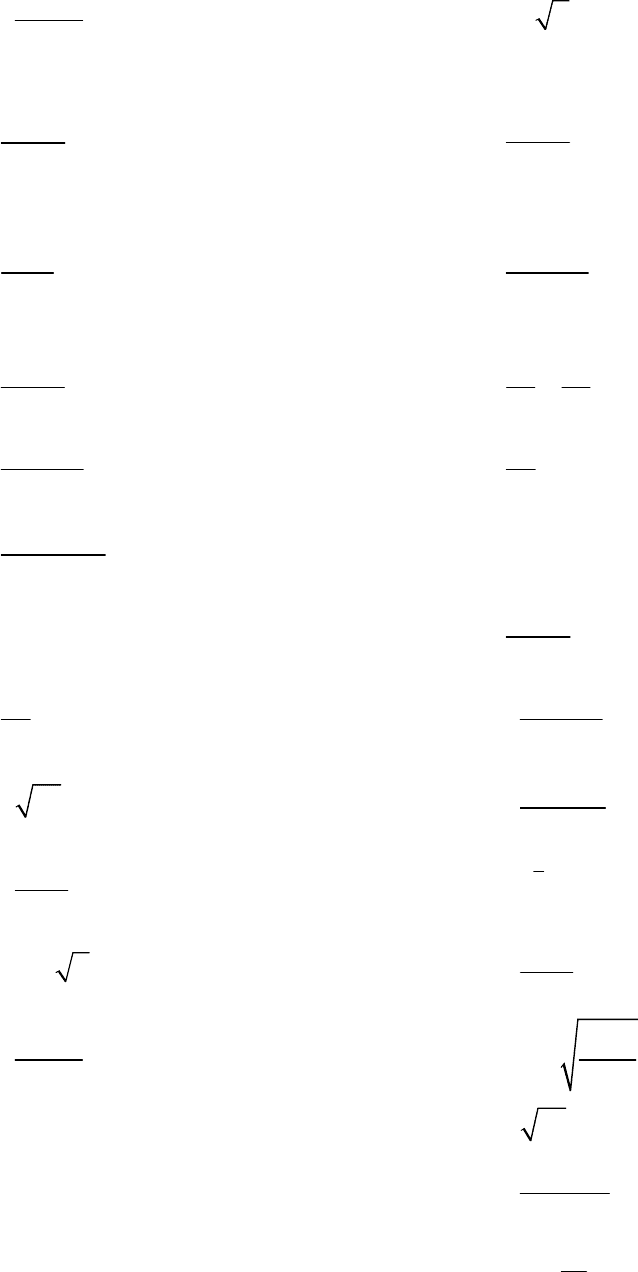
3
19)
2
9
x
y =
; 20)
84yxx x
=
−+
.
x
−
4.35. Найти асимптоты кривых:
1)
2
1x
y
+
=
2
x −
; 2)
2
2
1
x
y
x
=
−
;
3)
e
x
yx
−
=
; 4) lnyxx
=
;
5)
2
5
1
x
y
x
= ; 6)
−
2
2
5
y
x
x
=
−
.
функции и построить ее графи4.36. Провести полное исследование к:
1)
2
2
1
x
y
x
=
−
; 2)
53
53
x
x
y
=
− ;
3)
4
x
y
3
(1 )
x
=
;
+
4)
2
x
x
y
e
=
;
5)
2
1x
2
y
1
x
x++
+
2
=
;
ln( 2)yx x
6)
=
+
;
7)
39
;
32
yx x x=− −
8)
2
2
1
1
x
y
x
+
=
−
;
9)
4
3
x
yx=+
;
4
10)
2
29
2
x
y
x
−
=
+
;
2
3
1yx=−
; 12)
(
)
11)
2
1x
y
+
=
;
2
x
−
13)
2
2
1
x
y
x
=
+
; 14)
1
3
x
y
=
;
15)
yx x=−
; 16)
3
1
x
y
x
=
+
;
17)
4
3
2
x
y
x
=
−
; 18)
3
2
6
x
y
x
=+
−
;
19)
2
(1)(2)yx x=+ −
; 20)
2
3
1yx
=
−
;
21)
x
yxe
−
=+
; 22)
2
5( 2)x
y
x
−
=
;
23) ln( 1)
yx x=− +; 24)
ln
yx
x
=
+ .
67
Задания для индивидуальной работы № 10
наименьшее значения функции
Таблиц 1
Задание 10.1. Найти наибольшее и
()
yfx= на заданном промежутке (табл. 10.1).
а 10.
Номер
()
yfx
варианта
=
промежуток
1
22
ln
x
x
y
x
−
+
=
[1;2)
x
∈−
2
21
2
x
ye
−
=+
12
73
x
e x
−
+−
[0,14;1
x
∈
)
3
22 92 12
32
[1;1]
x
∈−
2
x
xx
y =⋅ −⋅ + ⋅
4
2
log 2 log 8yxx=−
22
1x
⎡
∈
⎣
/2; 2 2
⎤
⎦
5
2
cos sin
x
yx=
2
[0; ]
x
π
∈
6
2
2
3
1
x
x
y
+
=
−
[2;0]
x
∈−
7
1
[1; 4]
x
∈
ln ln 2
2
yxxx=−
8
1
(3)
x
yx e
+
=−
[2;4]
x
∈−
9
2
(3)
x
yx e
=−
[1;4]
x
∈−
10
2
lnyx x=
[1; ]
x
e∈
11
[0;8]
x
∈
3
3yx x=+
12
x
yxe
−
=
[0; )
x
∈+∞
13
2
130yx=−
[7;8]
x
∈−
14
1
;
1
arctg lnyxx=−
2
3
3
x
⎡⎤
∈
⎢⎥
⎣⎦
15
1
1
x
y
x
−
[
=
+
;4]
x
∈−∞
16
2
1
2ln
[2; )
x
∈+∞
yx x
x
=+−−
17
1
arctg
1
x
y
x
−
=
[0;1]
x
∈
+
18
3
1
x
y
x
=
+
[1; )
x
∈+∞
19
[0;3]
x
∈
22
3
(2)yxx=−
20
2
2
1
1
x
y
x
x
+
=
++
[0; )
x
∈+∞
68
69
Окончание табл. 10.1
21
1
(3)
x
yx e
+
=−
[2;4]
x
∈−
22
2
21
3
x
x
y
+−
=
[2;0]
x
∈−
23
1
ln ln 2
2
yxxx=−
[1; 4]
x
∈
24
sin 2
yxx=− [0; ]
x
π
∈
25
2
1
33
x
y
xx
−
=
−+
(; )
x
∈−∞+∞
26
3
2
2
x
y =
[8; 1]
x
∈− −
27
2
2
1
3
x
x
y
x
++
=
+
(; )
x
∈−∞+∞
28
2
3
yxx=− −
[1; )
x
∈+∞
29
2
1
33
x
y
xx
−
=
−+
(; )
x
∈−∞+∞
30
2
(3)
x
yx e=−
[1;4]
x
∈−
Задание 10.2. Провести полное исследование функции и построить ее
график (табл. 10.2).
Таблица 10.2
Номер
варианта
Номер
варианта
1
3
2
4x
y
x
−
=
16
2(2 )
2(2 )
x
e
y
x
+
=
+
2
3
2
12
x
y
x
−
=
17
2
8
4
x
y
x
=
+
3
2( 1)
2( 1)
x
e
y
x
−
=
−
18
2
8
4
x
y
x
=
−
4
3
2
32x
y
x
−
=
19
2
1
1y
x
⎛⎞
=+
⎜⎟
⎝⎠
5
3
2
1
x
y
x
=
−
20
ln
2
x
y
x
=
+
6
3
3
x
e
y
x
−
=
−
21
2
1
x
y
x
=
−
7
2
2
1
x
y
x
+
=
−
22
2
2
(1)
x
y
x
=
−
70
Окончание табл. 10.2
8
2
2
1
x
y
x
=
−
23
2
12
9
x
y
x
=
−
9
2
21
(1)
x
y
x
−
=
−
24
2
12
9
x
y
x
=
+
10
2
2
1
1
x
y
x
+
=
−
25
2
2
x
e
y
x
−
=
−
11
2
2
1
yx
x
=+
26
22
lnyx x=−
12
2
2
1
x
y
x
−
=
27
1
yx
x
=
+
13
2
1
x
y
x
=
+
28
3
1
x
y
x
=
−
14
2
2
(1)x
y
x
−
=
29
3
1
x
y
x
=
+
15
2
x
yxе
−
=
30
2
1
4
yx
x
=
+
