Румянцев Н.В., Медведева М.И., Полшков Ю.Н., Пелашенко А.В. Практикум по решению задач курса Высшая математика
Подождите немного. Документ загружается.

1)
1fx x=−
; 2)
2
3
()
f
xxx
=
−()
.
4.25. К кривой
1
провести касательные параллельные
прямой 0
42
23yx x x=− +−
31
x
y−+=.
4.26. Найти уравнение горизонтальной касательной к графику функции
x
x
ye e
−
=+
.
4.27. Найти координаты точки пересечения двух касательных, роведен-
ных к графику функции
п
2
1
3
x
y
x
+
=
−
в точках с абсциссами
2
x
=−
и
4
x
=
.
4.28. Используя правило Лопиталя, вычислить пределы:
1)
()
1
tg
2
lim
ln 1
x
x
x
π
→
⎛⎞
⎜⎟
⎝⎠
−
3
2
0
41
lim
sin 5
x
x
ex
x
→
−−
; 2)
;
3)
(
)
1
ln 1
lim
ctg
x
x
x
π
→
−
; 4)
0
sin 3
lim
x
x
x
→
;
5)
0
m
→
⎜
⎝
11
li
⎛⎞
−
; 6)
1
x
x
xe
⎟
−
⎠
2
1
lim
x
e
0
sin 3
x
x
→
−
;
2
1
2
tg
8)
0
1cos5
lim
1cos3
x
x
x
→
−
−
0
m(1li sin )
x
x
x+ ;
→
7)
;
9)
2
0
sin
lim
x
x
x
x
→
−
(
)
tg
0
lim sin
x
x
x
→
; 10) ;
11)
(
)
1
2
lim sin(2 1 tg
x
)
x
x
π
→
−⋅
; 12)
0
tg sin
lim
sin
x
x
x
x
x
→
−
−
;
13)
()
1
ln
lim ln 2
x
x
x
→+∞
()
2
ctg
0
lim cos
x
x
x
→
; 13) ;
14)
0
ln
lim
ctg
x
x
x
→
2
3
ln
lim
x
x
x
→∞
; 14) ;
15)
2
2
0
ln cos(4 3 )
lim
sin5
x
x
x
x
→
; 16)
−
()
0
lim tg
2
x
x
x
→
π−
;
17)
k
x
x
a
; 18)
0
11
lim
ln
x
x
x
→
⎛⎞
−
⎜⎟
⎝⎠
0
lim
x→
;
19)
0
2
lim
1cos2
xx
x
ee
x
−
→
+
−
−
0x
lim ln
x
x
; 20)
→
;
21)
22)
sin
0
1
lim
x
x
x
→+
⎛⎞
⎜⎟
⎝⎠
0x
1
lim ctg
x
x
⎛⎞
−
⎜⎟
→
⎝⎠
; ;
23)
lim(ln ctg )
tg
0
x
x
x
→
; 24)
2
0
1
lim ln 1
x
xx
x
→
⎛
⎛⎞
−+
⎜⎟
⎜
⎝⎠
⎝⎠
⎞
⎟
.
51

Задания для индивидуальной работы № 9
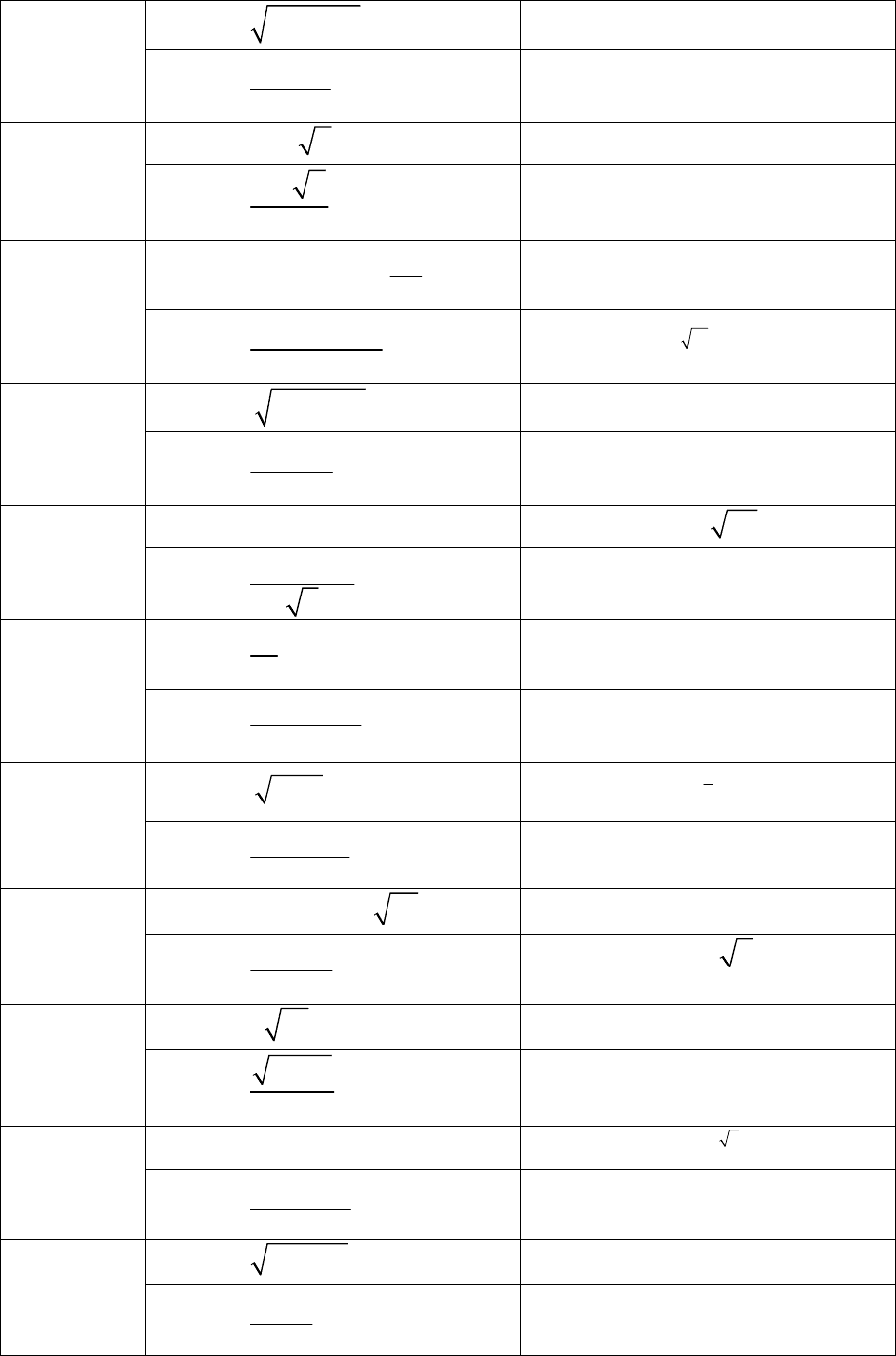
Задание 9.1. Найти первые производные функций (см. табл. 9.1):
Таблица 9.1
варианта
Номер
2
3
(2)
x
yx e
−
=++
sin 2 lnyxx
=
⋅
1
2
3
cos(3 1)
x
y
x
=
−
(
)
cos 5 1
arcsin 2
x
y
+
=
cos3 lnyx=+
x
7
2tg3
x
yx=⋅
2
3
sin( 3)
x
y
x
=
−
arccos
5
3
x
y =
22
3
(2 1) tg( 1)х x−+ +
3
sin 2
x
yxe
=
⋅
3
2
cos
x
y
x
=
21
arctg3
x
y
+
=
3
2
ctg2 logyx=+
x
3
cos 2yx x=⋅
4
sin 2
x
x
y
e
=
arcsin
3
x
y =
23
sin 5
x
yx=+
3
ln(2 3) ( 1)yxx
=
+⋅+
5
3
cos3
x
y
x
+
=
3
arccos tgyx=
3
log 2 tg(2 1)yxx=+
−
2
33
x
yx1
=
⋅−
6
sin 1
x
y
x
+
=
23
cos 2
x
y =
3
3
ctg 2 3
x
yx=+
2
tg3 ( 1)yxx
=
⋅−
7
2
cos 4
2
3
x
x
x+
5
ln 2 3
3
x
y =
−
y =
3
5 1 arctg( 2)
yx x=−+ −
(
)
5
ctg 2yxx
π
=
−⋅
8
2
cos 2
x
x
y
x
+
=
3
sin arctg2
x
y
−
=
cos ln(2 )yx=+−
2
csin 3ar
x
yxe
−
=
⋅
x
9
4
3ln
1
x
x
y
x
+
=
−
3
2
arcctg
3
x
y =
3
tg 3 1yx x=++
3
3
log 2yx
=
⋅−
10
2
(3 )
2
x
x
y
+
=
25
arccos lnyx=
52
Продолжение табл. 9.1
3
5
(1 2 ) tg 2yx=− + x
2
3sin2
x
yx=⋅
11
2
3
cos 2
x
x
y
x
+
=
2
5
log sin 2
x
y =
sin
3
log 2
x
yx=+
3
arctgyxx
=
⋅
12
sin5
x
x
y
x
+
=
2
arccosln( )yxx
=
+
1
ctg(2 1)
2
yx
x
=−+
2
tg3 3
x
yx
−
=
⋅
13
(
)
3
cos 3
x
y
x
π
−
=
3
arcsin
x
ye=
22
3
(1 2 ) 2
х
y х
−
=− +
2
arctg( 1) 3
x
yx
=
+⋅
14
2
2
2
y
3
x
x
x
=
−
cosln 2
x
y =
sin
ctg2 2
x
yx=+
arctg 2yxx
=⋅
15
3
x
ln(2
y
1)x
−
=
2
ln sin (y 2)x
=
+
cos
5
3
x
ye
х
=+
yxx
22
sin
=
⋅
16
31
cos(2 )
x
y
+
=
2
sin 3
tg7
x
−
x
y =
2
sin 2
x
yx
−
=+
2
3
tg3yxx
=
⋅
17
sin 3
4
x
x
y
1
+
=
32
sin
5
x
y =
23
9
log sinyxx=+
(ln 1)yxx
2
ctg
=
⋅+
18
cos3
ln
x
y
x
x
=
+
sin
arctgyx=
223
2
x
y
х
e=+
33
cos 2
x
yx
=
⋅
19
31
sin 2
x
y
x
−
=
2
arcctg sin( 5)yx
=
−
32
ln (2 ) 3
x
yx=++
ctg5 2
x
yx
=
⋅
20
2
sin3
2
x
x
y
+
=
2
2
sin logyx=
2
2
3
x
yxxe=−+
3
tg ln 3yxx=⋅
21
2
3
1
x
y
x
=
+
2
5
log arcsinyx=
53
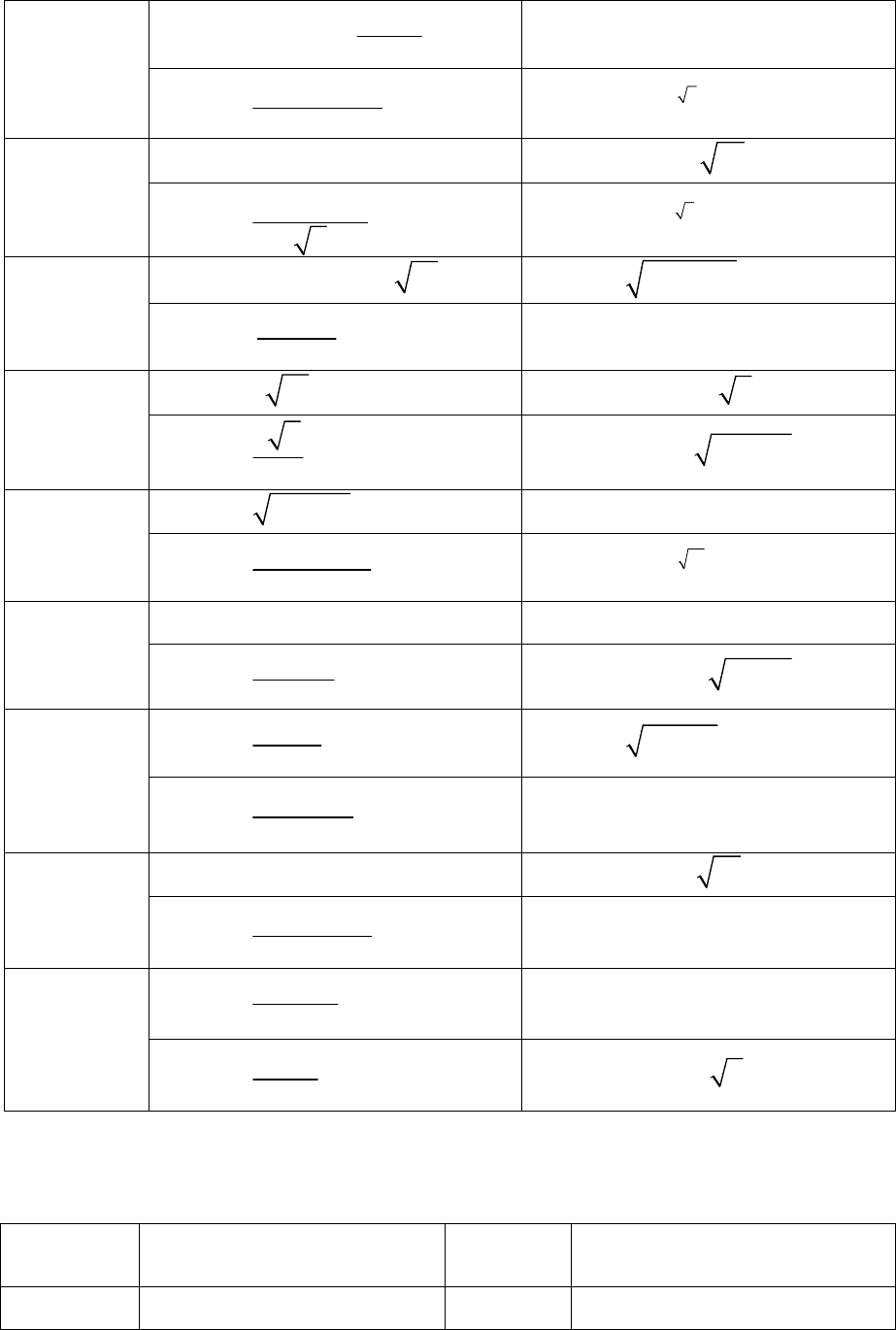
Окончание табл. 9.1
2
3
sin 2
21
yx
x
=+
−
21
10
x
yx
0
=
⋅
22
()
sin 2
2
x
x
y
π
−
=
arcctg
x
ye=
2
3
log sin 2
x
yx=+
223
sinyx=⋅
x
23
2
3sin
x
x
y
x
+
=
sin 7
x
y =
3
cos(2 1)yx=−+
x
2
3
(2 1) sin3yx=−⋅ x
24
5
log 2
sin
x
y
x
=
cos 3
ctg2
x
y =
5
4
5sin2
x
y х=+
2
cos 2yxx
=
⋅
25
2
3
5
x
x
y =
23
arcsin 2yxx
=
−
235
2
2logy
х
х x=−+
21 2
sin
x
ye x
−
=⋅
26
cos(3 1)
23
x
x
y
+
=
3
arcctg
5
x
y =
2
2
sin 2
x
yx=+
(
)
5
tgyx
π
x
=
−⋅
27
ln
2
x
x
x
y
+
=
2
3
log sinyxx
=
−
sin
5
32
x
ye
х
=+
−
23
21sinyx=−⋅
x
28
5
3
sin(1 )
x
y
x
=
−
2
tg ln( 1)yx
=
+
3
sin 2
x
yx
−
=+
223
ctgyx=⋅
x
29
2
3cos
ln
x
x
y
x
+
=
2
tg
sin 2
x
y =
5
4
cos
(2)
x
ye
х
=+
+
2
cos 5
x
yx
=
⋅
30
1
3
sin 3
x
y
x
+
=
3
ctg logyx=
Задание 9.2. Вычислить прои торого порядка (см. табл. 9.2):
а 9.2
Номер
варианта
звод ую вн
Таблиц
Номер
варианта
1
y= x
2
in 2xx+
16
y=+s
3
2ln
х
54
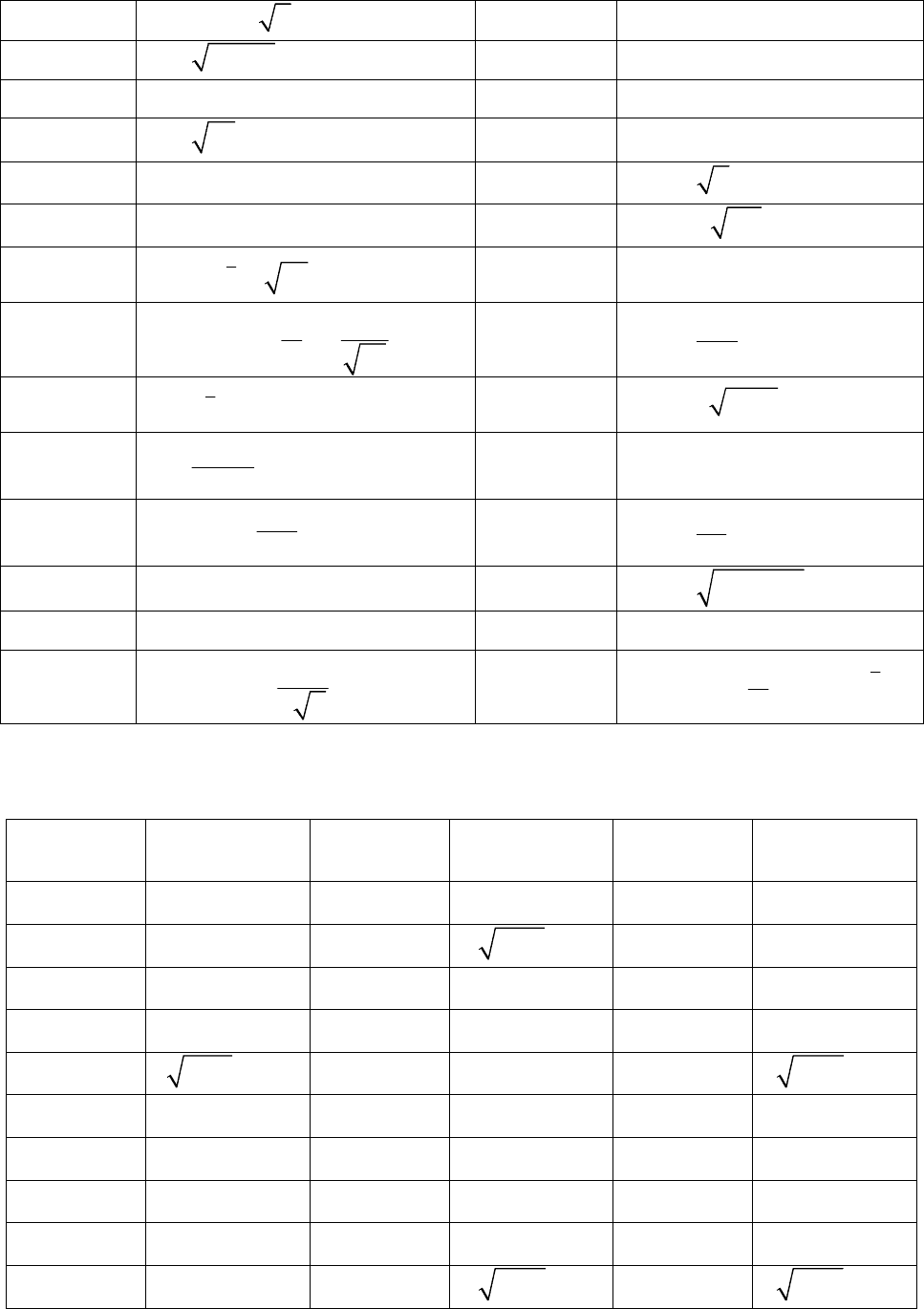
Окончан бл. 9.2
2
ие та
17
x
cos(2 3) 2
yx=−+
2
5
x
y е x
−
=++
3
5
23logy
2
х
x=++
18
2
10 (
х
y
−
=+
3)х −
4
tg3 3
21
x
yx=+
19
−
5
3sin3y
х
x=−
5
2
3
ln( 3)y х x=+ +
20
1
cos5
2
2
x
yx
+
=−
e
−
6
2
212n
х
yx=−
21
si
2
3
lny
х
x=+
7
(
)
3
2sin 3yxx
π
−
=++
22
1
3
2ln3y
х
x
−
=+
8
47
5
10
x
y
х
−
=+
3 2
235
х
y
х
е
−
=+−
9
3
4
3
cosyx
4
x
π
⎛⎞
=−
⎜⎟
+
24
21
3
1
3
2
x
y
−
=+
⎝⎠
x
10
7
2
73log
x
yx=+
25
33y 2sin5
х
x=−+
11
2
3
31
x
y
х
=+
−
26
arctg2
yx=
12
2
1
x
y
2
3
e
x
−
=+
27
()
sin 6
5
yx
х
π
=+ −
3
13
23
32 21
х
y хх=− +
28
2
3
+
(3 cos 2y 1)
х
x=+ +
14
(5 1)
10 5
x
y
х
е
−
29
x
2ln3 sin(2 )
yx=+−
=−+
15
3
1
logyx
2
x
=+
30
5
cos 3
3
x
yxe
π
⎛⎞
=−+
⎜⎟
⎝⎠
Задание 9.3. Вычислить приближенно (см. табл. 9.3):
Таблица 9.3
Номер
варианта
Номер
варианта
Номер
варианта
1
0
sin 29
11
0
cos61
21
tg61
0
2
2
log 2,02
12
3
8,02
22
0
cos 44
3
0
cos 46
13
log 2,98
23
log 1,99
3 2
24
4
0
tg29
14
0
sin 31
0
sin 44
5
15
25
0
cos31
3
7,99
3,99
6
in5
16
0
tg59
26
tg31
0
s 9
0
7
3
log 3,01
17
0
cos59
27
log 2
3
,99
8
0
сtg31
0
t 6
28 18
g4
0
cos 29
9
sin
19
0
sin 61
29
5
log 4,99
0
46
10
0
tg44
20
4,0
30
2
3
7,98
55
Задание 9. табл. 9.4):
Таблица 9.4
4. Найти пределы, используя правило Лопиталя (
Номер
варианта
Номер
варианта
1
2
0
sin
lim
x
x
x
x
→
−
16
0
tg3
lim
21
x
x
x
→
−
2
2
ln(
lim
x
17
0
lim
ln(1 )
x
х
x
→
+
2 3 )
25
x
xx
→∞
+
+
+
3
0
tg
lim
x
x
x
x
→
−
18
0
51
lim
arc tg
х
x
x
→
−
4
2
0
lim
sin 3
x
ехcos
x
x
→
19
−
2
cos 2
lim
0
sin
x
x
x
x
x
→
−
−
5
2
0
arc tg
lim
x
x
x
→
20
3
2
2
lim
х
x
x
→∞
6
0
n(1 )
1
x
x
l
lim
x
e
→
+
−
1 2
2
0
lim
x
x
sin
x
x+
→
7
0
21
lim
x
arcsin 2
x
x
→
22
−
3
2
0
21
lim
7
х
x
x
х
→
−
+
8
2
0
31
lim
x
x
23
3
tg
x
→
−
lim
х
x
х
е
→
∞
9
24
3
lim
х
x
х
2
0
е
→∞
arcsin
lim
1
x
x
x
e
→
−
10
2
0
31
lim
ln(1 )
x
x
x
→
−
+
25
2
3
lim
ln(1 )
х
x
x
→∞
+
11
2
ln(1 2 )
lim
x
x
x
→∞
+
26
0
1
x
е
lim
sin 3
x
x
→
−
12
0
arcsin
lim
x
x
x
→
27
0
tg3
lim
sin
x
x
x
x
→
+
13
0
2cos
lim
x
x
sin
x
x
→
−
28
2
31x
2
lim
х
x
х
е
→∞
+−
14
29
2
0
tg
lim
x
x
x
x
→
−
2
0
lim
3cos2
x
x
х
x
→
−
15
0
sin
lim
arc tg
x
x
x
x
→
+
30
0
sin
lim
tg2
x
x
x
x
→
−
56
ТЕМА 4
ПРИМЕНЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧЕСЛЕНИЯ
К ИССЛ ФУНКЦИИ
ЕДОВАНИЮ
Признаки монотонности функции
Пусть функция ()
f
x определена и непрерывна на отрезке [;]ab ()
f
x и
дифференцируема на интервале (;)
ab . Тогда:
1)
функция ()
f
x является неубывающей (невозрастающей) на [;]ab то-
гда и только тогда, когда
() 0fx
′
≥
(
() 0fx
′
≤
) для всех
x
из ; (;)ab
2)
функция ()
f
x является убывающей (возрастающей) на тогда и
толь
[;]ab
ко тогда, когда
() 0fx
′
>
(
() 0fx
′
<
) для всех
x
из (;)ab .
Пусть функция ()
f
x определена и непрерывна на отрезке [;]ab и ()
f
x
дифференцируема на интервале (;)
ab . Функция ()
f
x является постоянной на
(;)
ab тогда и только тогда, когда
() 0fx
′
=
всех
x
из (;)ab .
Экстремумы функции
Точка
0
x
называется точкой минимума (максимума) функции ()
f
x , если
она точки и для каждой точки
0
x
x
≠
определена в некоторой окрестности этой
этой окрестности
0
() ( )
f
xfx≥
(соответственно
0
() ( )
f
xfx
≤
). Значение функции
0
()
f
x
функции).
ся либо минимум, либо максимум.
называется минимумом функции (соответственно максимумом
Под
экстремумом понимает
Точка
0
x
из области определ ()
f
x ения функции называется критической
точкой
, если функция ()
f
x дифференцируема в точке x
0
и
() 0fx
′
=
, или ()
f
x
не дифференцируема в точке
0
x
.
Необходимое условие экстремума.
Если
0
x
– точка экстремума функции ()
f
x , то
0
x
– ее критическая точка.
Достаточные условия экстремума.
1.
Пусть функция ()
f
x непрерывна в некоторой окрестности критической
точки
0
x
. Если при переходе через точку
0
x
производная функции меняет знак
«+» на «–», то
0
x
0
x
– точка макс рез точкуимума; если при переходе че производ-
ная функции меняет знак «–» на «+», то
0
x
– точка минимума; если при п
точку
ереходе
через
0
x
0
x
производная не меняет знак, то в точке экстремума нет.
0
x
функция ()
f
x
2.
Пусть в критической точке дважды дифференцируе-
ма. Если при этом
() 0fx
′′
<
, то в точке
0
x
ункция достигает максимума;
() 0fx
′′
>
, то в точке
0
ф
x
функция достигает минимума.
3.
Пусть функция ()
f
x задана параметрически:
57
(), ()
x
ut y vt==,
нкции ()
t и ()vt в некотором промежутке изменения аргумента
t
имеют
рядка, причем
() 0ut
где фу
производные первого второго по
u
и
′
≠
. Пусть при
0
tt
=
() 0vt
′
=
. Тогда если
0
() 0vt
′
′
<
, то ф xункция yf()
=
при
00
()
x
xut
=
=
имеет
ия ()yfx
максим ; если
vt
′′
ункц
ум
0
() 0>
, то ф
=
при
00
()
x
xut
=
=
имеет мини-
0
ичие экстремума остается открытым. Точ-
ки, в кот
() 0vt
′′
=
требуют специального
мум; е
вопрос о нал
о
исследования
функции, непрерывной на отрезке
, достигается или в критических точках функции или на концах отрезка.
того, чтобы найти наибольшее (наименьшее) значение функции на отрезке
ение функции во в
сли
() 0vt
′′
=
, то
рых
.
Наибольшее и наименьшее значения функции
Наибольшее (наименьшее) значение
[;]
ab
Для
[;]
ab надо вычислить знач сех критических точках на отрезке
[;]
ab , значения ()
f
a , ( )
f
b на концах отрезка и выбрать наибольшее (наи-
мень ученных ачений.
Выпуклость и вогнутость функции.
цируема на интервале
кривая
выпукла, т.е ниже своей касательной; если в
интер
шее) из пол зн
Точки перегиба
Пусть функция ()yfx= определена и дифферен
Если
() 0fx
′′
<
в интервале (;)ab , то в этом интервале
(;)
ab . ()yfx=
. ее
лежит любой
() 0fx
′′
>
график
вале (;)
ab , то в этом интервале кривая ()y xf
=
вогнута, т.е. ее график
лежит выше любой своей касательной.
сли
или не существует, но
Е
0
()0fx
′′
=
0
()
f
x
′
существует и вторая произ-
водная
()
f
x
′′
меняет знак при переходе через точку
0
x
, то точка
(,())
00
x
fx
яв-
а кр
усть
ляется
точкой перегиб ивой ()yfx= .
Асимптоты
(, )
M
xy − некоторая точка графика функции ()yfx
=
П . Говорят, что
точка
M
удаляется в бесконечность по графику, если она движется по графику
так, что или
x
→±∞
, или .
y →±∞
Прямая линия называется
асимптотой графика функции ()yfx= , если
расстояние от точки
M
, лежащей на кривой, до этой прямой нулю
при движении точки
стремится к
M
вдоль какой-нибудь ветви кривой в бесконечность.
Различают вертикальные, горизонтальные и наклонны асимптоты.
Если
е
lim ( )
xa
fx
→
=
∞
,
58

то прямая
x
a=
является вертикальной асимптотой графика функции
. Вертикальная асимптота параллельна оси .
()
yfx= Oy
Если
lim ( )
x
f
xc
→±∞
=
,
то прямая
является горизонтальной асимптотой графика функции
=
yc=
()
x (правая при yf
x
→
левая при
+∞
и
x
→−∞
). Горизонтальная асимптота
параллельна оси
.
Если существуют пределы
Ox
()
lim
x
f
x
k
x
→± ∞
и
→± ∞
=
kx lim ( ( ) )
x
bfx
=
− ,
то прямая – наклонная асимптота. Заметим, что горизонтальную асим-
клонной при
ykxb=+
птоту можно рассматривать как частный случай на асимптоты
0k
=
.
ия функции;
2) найти точки пересечения графика с осями координат;
3 вать функцию н , сть и периодичность;
йти то
ислить экстремальные
значения
функц функции;
6 айти то функции, исследовать функцию на на-
правление выпуклости;
7
8) построить график функции.
рафик ункции можно строить в следующей последовательности.
нане ;
2
3) нанести точки экстремума;
4) нанести чки перегиба;
5) при
необходимости исследовать поведение функции при
Общее исследование функции и построение ее графика
Общее исследование функции и построение ее графика можно проводить
по следующей схеме:
1) найти область определен
) исследо а четность нечетно
4) исследовать функцию на непрерывность, на чки разрыва и выяс-
нить характер разрывов;
5) найти точки экстремума функции, выч
ии, установить интервалы монотонности
) н чки перегиба графика
) найти асимптоты графика функции;
Г ф
1) сти точки пересечения с осями координат
) начертить все асимптоты;
то
x
→±∞
;
6) начертить схематично кривую через нанесенные выше точки, учитывая
поведение графика вблизи асимптот и при
x
→±∞
;
7) полученный эскиз сравнить с результатами исследования: проверить
проме лости и вогнутости и т. д.
жутки монотонности, промежутки выпук
59
Примеры решения задач
ункции
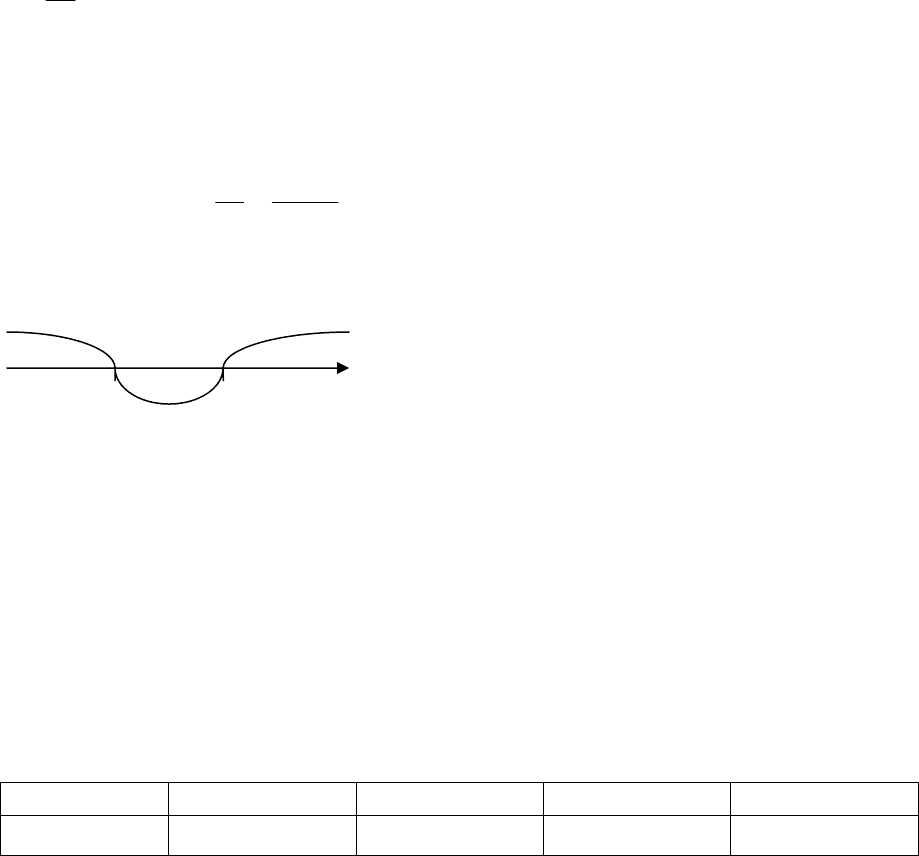
Пример 4.21. Найти интервалы возрастания и убывания ф
2
4
yx
x
=+ .
Решение. Область определения функции ) (;0)(0;
x
∈
−∞ +∞∪ . Найдем
произ авна
водную данной функции и точки, в которых производная р нулю или
не существует:
3
3
33
88
1080
x
yx
xx
−
′
=−
2x
= = ⇔ −= ⇔ =
.
ой функции на три интерва-
1).
Точка
0
2x =
– критическая точка, она разбивает область определения
рассматриваем
ла (рис. 4. В каждом из этих промежут-
ков производная
()yx
′
сохраняет знак
(знак производной отмечен на рис. 4.1.).
Тогда данная функция возрастает на про-
межутках
и
(;
+ +
0
− 2 х
Рис. 4.1.
0)
−∞ (2; )
+
∞ и убывает на промежутке
Пример 4.22. Найти экстремумы функции
(0;2) .
22
(1)(1)yx x
=
−+
.
Решение. Функция определена и дифференцируема на всей числовой оси.
айдем ее критические точки. Так как
,
то кр ие точки –
x
. Сос
Н
22
2( 1)( 1) 2( 1) ( 1) 4 ( 1)( 1)yxx x x xxx
′
=−++− += −+
итическ
123
, 1, 1xx===−
тавим таблицу знаков произ-
водной на интервалах между критическими точками:
Интервалы
1
0
x
<−
10
x
−
<<
01
x
<
<
1
x
>
Знак
()yx
′
−
+
−
+
Тогда
1
x
=−
и
1
x
=
– точки локального минимума и
yy=−
Точка
min
(1) (1) 0y= =
.
0
x
=
– точка локального аксимума и
yy==
Прим на м функцию
xx>
⎧
м
max
(0) 1
.
ер 4.23. Исследовать экстрему
2, 0,
34, 0.
xx
−− ≤
⎩
Решение. Несложно заметить, что точка
0
y
=
⎨
x
=
– точка разрыва функции.
Производная данной функции
2, 0,
3, 0
x
y
x
>
⎧
=
⎨
−<
⎩
60
