Румянцев Н.В., Медведева М.И., Полшков Ю.Н., Пелашенко А.В. Практикум по решению задач курса Высшая математика
Подождите немного. Документ загружается.

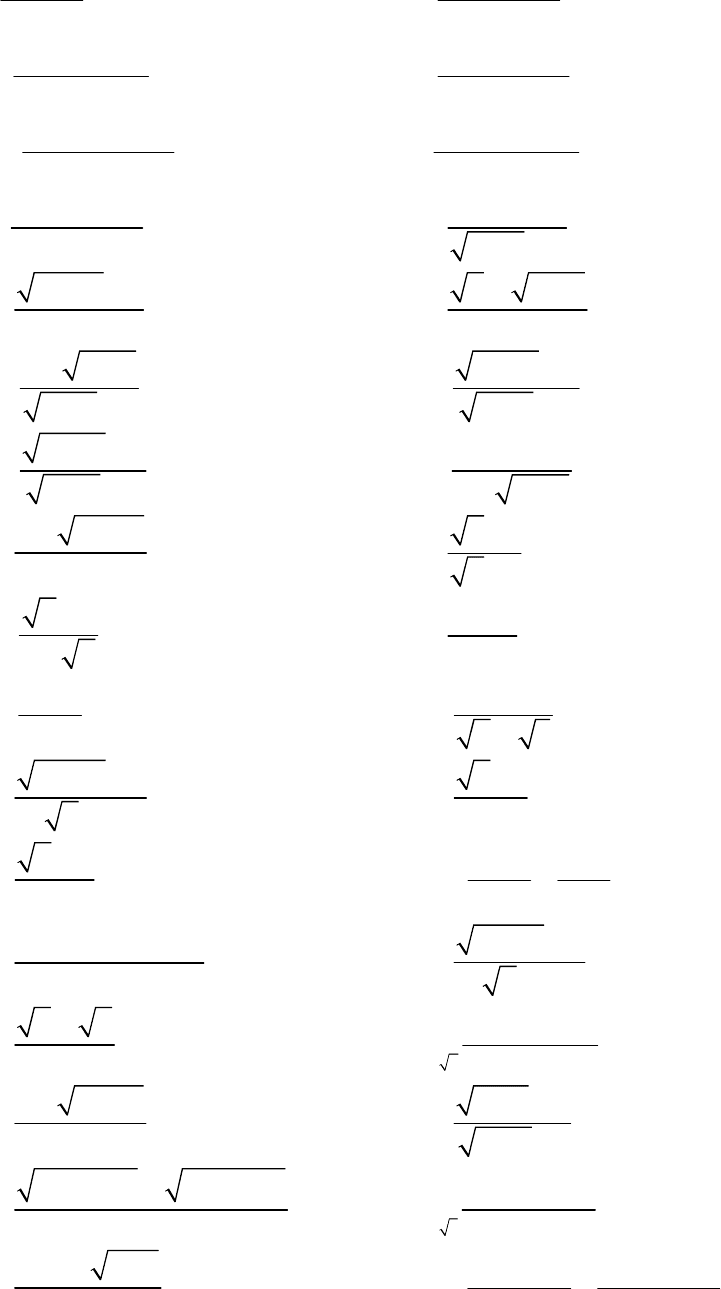
3)
3
3
3
lim
27
x
x
x
→
−
−
; 4)
2
2
1
45
lim
23
x
xx
x х
→−
−
−
−
−
;
5)
2
2
3/2
23
lim
25
x
xx
xx
→
3
−
−
−+
; 6)
2
2
1
32
lim
2
x
1
x
x
х x
→−
+
−
−
++
;
7)
2
2
1/2
274
lim
25
x
xx
xx
→−
3
−
−
−++
; 8)
2
2
3
311
lim
25
x
xx
xx
→
6
3
−
+
−
−
;
9)
2
3
1/3
32
lim
27 1
x
1
x
x
x
→
+−
−
; 10)
0
lim
42
x
x
х
→
+
−
;
11)
3
23
lim
3
x
х 3
x
→
+
−
−
; 12)
1
2
lim
1
x
х
х
x
→
−
−
−
;
13)
2
26
lim
73
x
х
х
→−
−+
−−
; 14)
2
41
lim
22
x
х
х
→−
3
+
−
+
−
;
15)
2
41
lim
22
x
х
х
→−
3
+
−
+
−
; 16)
1
1
lim
2
x
х
хх
→−
+
+
+
;
17)
2
4
3
lim
16
x
хх
х
→
−+
−
4
; 18)
3
1
1
lim
1
x
х
х
→
−
−
;
19)
3
64
8
lim
4
x
х
х
→
−
−
; 20)
2
2
4
lim
2
x
x
x
→
−
−
;
21)
3
1
1
lim
1
x
x
x
→−
+
+
; 22)
3
3
lim
3
x
x
x
→
−
−
;
23)
9
72 5
lim
3
x
x
x
→
+−
−
; 24)
3
2
1
1
lim
1
x
x
x
→
−
−
;
25)
3
1
lim
1
x
x
x
x
→
−
−
; 26)
3
1
31
lim
11
x
x
xx
→
⎛⎞
−
⎜⎟
−
−
⎝⎠
;
27)
3
32
0
(1 ) (1 3 )
lim
x
x
x
xx
→
+−+
+
; 28)
3
8
92 5
lim
2
x
x
x
→
+
−
−
;
29)
3
4
2
1
lim
1
x
x
x
x
→
−
−
; 30)
42
3
2
44
lim
2
x
xx
x
x
→
−
+
−
;
31)
2
2
32
lim
4
x
xx
x
→
−−
−
; 32)
1
52
lim
21
x
x
x
→
−
−
−
−
;
33)
22
2
0
11
lim
x
x
xxx
x
x
→
++ − −+
−
; 34)
2
42
3
3
lim
23
x
x
xx
→
−
−
−
;
35)
2
2
(2)
lim
4
x
xx
x
→
−−
−
1
; 36)
22
2
11
lim
(2) 32
x
xx x x
→
⎛⎞
−
⎜⎟
−
−+
⎝⎠
;
21
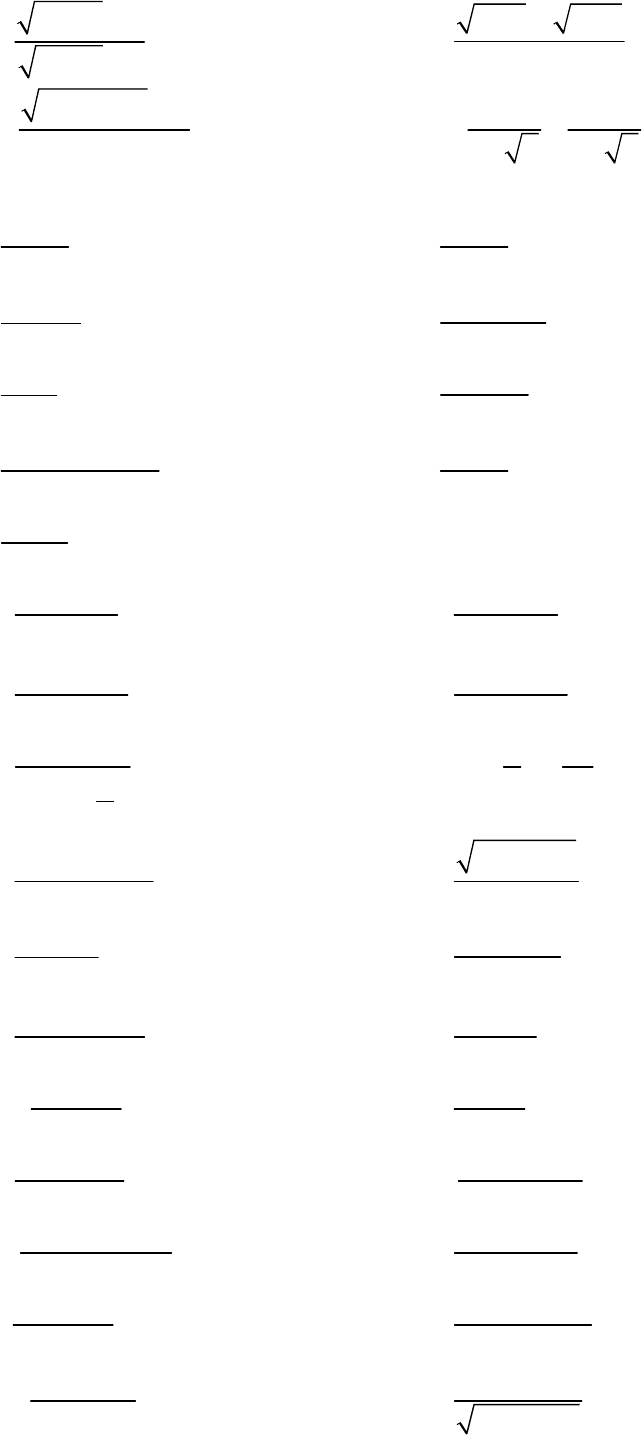
37)
2
2
0
42
lim
93
x
x
x
→
+−
+−
; 38)
33
0
11
lim
x
x
x
x
→
+
−−
;
39)
2
1
42
lim
1
x
xx
x
→−
++−
+
; 40)
3
1
32
lim
11
x
x
x
→
⎛⎞
−
⎜⎟
−−
⎝⎠
;
3.29. Используя первый замечательный предел, найти:
1)
0
sin 2
lim
x
x
x
→
; 2)
0
sin 2
lim
sin5
x
x
x
→
;
3)
2
2
0
sin 3
lim
sin 6
x
x
x
→
; 4)
0
1cos5
lim
sin5
x
x
x
x
→
−
;
5)
0
lim
tg2
x
x
x
→
; 6)
0
arcsin
lim
x
x
x
→
;
7)
0
sin
lim
sin 6 sin 7
x
x
x
x
→
−
; 8)
0
sin 7
lim
sin3
x
x
x
→
;
9)
0
tg6
lim
sin8
x
x
x
→
; 10)
2
0
lim ctg5
x
x
x
→
;
11)
2
0
1 соs3
lim
tg 6
x
x
x
→
−
; 12)
2
1
sin(1 )
lim
1
x
x
x
→
−
−
;
13)
0
4
lim
arcsin12
x
x
x
→
; 14)
2
0
sin 5
lim
arcsin10
x
x
x
→
;
15)
0
2
sin tg
lim
4sin
2
x
x
x
x
→
−
; 16)
22
0
5
lim ctg tg
84
x
x
x
→
;
17)
cos cos
lim
xa
x
a
xa
→
−
−
; 18)
2
0
1cos
lim
1cos
x
x
x
→
−
−
;
19)
3
3
0
sin
lim , ( 0)
sin
x
x
x
α
αβ
β
→
≠
; 20)
0
1cos6
lim
sin 3
x
x
x
x
→
−
;
21)
sin sin
lim
xa
x
a
xa
→
−
−
; 22)
2
3
1
sin
lim
sin
x
x
x
π
π
→
;
23)
/2
cos
lim
/2
x
x
x
π
π
→
−
; 24)
1
1
lim
sin
x
x
x
π
→
−
;
25)
2
2
sin( 2)
lim
4
x
x
x
→
−
−
; 26)
1
sin sin1
lim
1
x
x
x
→−
+
+
;
27)
2
cos 2 cos 4
lim
48
x
x
x
→−
−
+
;
28)
3
ctg3 ctg
lim
3
x
x
x
→
−
−
;
29)
5
tg5 tg
lim
tg( 5)
x
x
x
→
−
−
; 30)
7
cos cos 7
lim
sin sin 7
x
x
x
→
−
−
;
2
/3
1cos3
lim
tg 6
x
x
x
π
→
+
; 32)
0
|tg2 |
lim
1cos2
x
x
x
→
−
;
31)
22
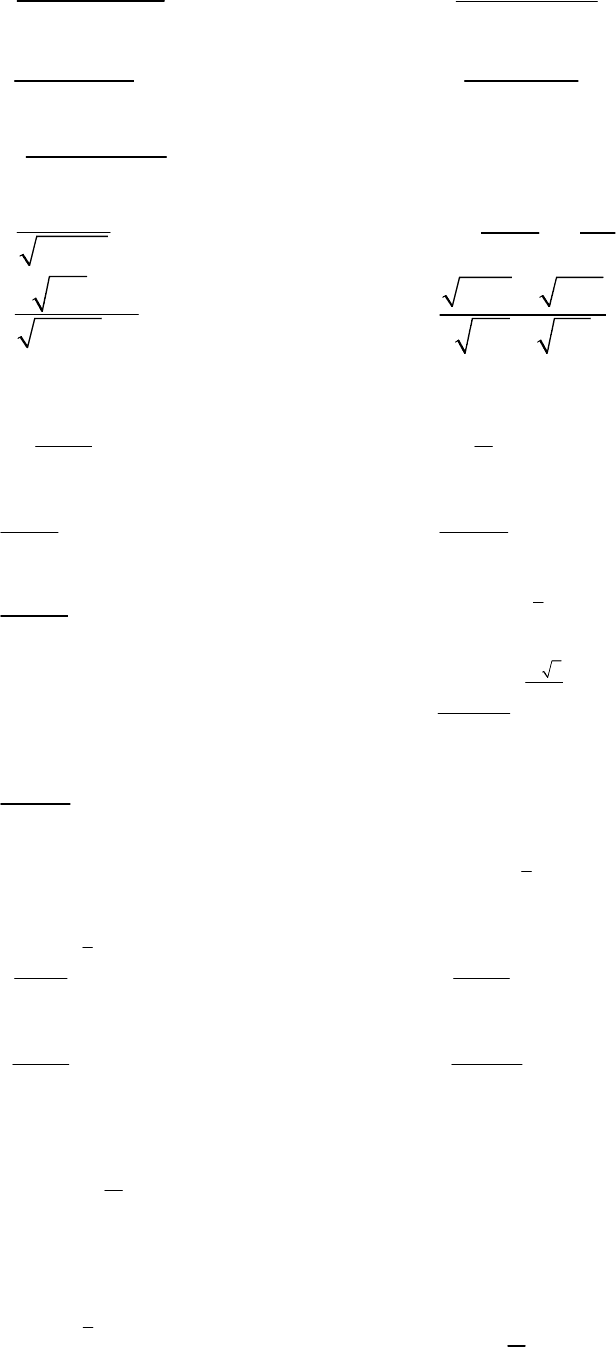
/4
1tg
lim
cos( / 4)
x
x
x
π
π
→
−
+
33)
; 34)
2
/6
14sin
lim
sin( / 6)
x
x
x
π
π
→
−
−
;
3
/3
8cos 1
lim
/2 /6
x
x
x
π
π
→
−
−
;
35)
36)
3
/6
8sin 1
lim
6
x
x
x
π
π
→−
+
+
;
37)
3
/3
8cos
lim
sin( /
x
x
x
π
π
→−
−
+
1
3)
38)
2
/2
lim (1 sin )tg
x
x
x
π
→
−
;
3
/4
ctg 1
lim
cos 2
x
x
x
π
→
−
;
39)
40)
4
4
lim sin ctg
22
x
x
x
π
→−
+
;
3
/4
tg 1
lim
sin 2 1
x
x
x
π
→
−
−
41)
; 42)
33
n1
li
x −
1
sin si
m
tg tg1
x
x
→
−
.
. Используя вто найти еду ие пределы: 3.30 рой замечательный предел, сл ющ
1)
1
lim 1
3
x
x
x
→∞
+
⎜⎟
+
⎝⎠
; 2)
5
4
lim 1
x
x
x
→∞
−
⎜⎟
⎝⎠
;
⎛⎞ ⎛⎞
1
3
lim
2
x
x
x
x
+
→∞
+
⎛⎞
⎜⎟
−
⎝⎠
; 4)
21
31
lim
33
x
x
x
x
→∞
+
⎛⎞
⎜⎟
−
⎝⎠
;
+
3)
1
41
lim
41
x
x
x
x
−
→∞
−
⎛⎞
⎜⎟
+
⎝⎠
; 6)
5)
()
1
0
lim 1 sin
x
x
x
→
+
;
7)
(
)
sec
0
lim 1 cos
x
x
x
−
→
+
; 8)
1
1
41
lim
42
x
x
x
x
x
−
−
→∞
+
⎛⎞
⎜⎟
−
⎝⎠
;
9)
2
2
1
lim
2
x
x
x
x
→∞
⎛
+
⎜⎟
+
⎝⎠
⎞
; 10)
lim [ln( 3) ln ]
x
x
xx
→∞
+
−
;
x
xx
→∞
11)
n( 2)]x
lim [ln l +
; 12)
1
0
lim(1 2 )
x
x
x
→
+
;
−
2
0
1
lim
1
x
x
x
x
→
+
⎛⎞
⎜⎟
−
⎝⎠
; 14)
2
lim
3
x
x
x
x
+
13)
→∞
⎛⎞
⎜⎟
+
⎝⎠
;
15)
23
li
1
m
3
x
x
x
x
→∞
+
⎛⎞
⎜⎟
+
⎝⎠
+
; 16)
1
21
lim
23
x
x
x
x
−
→∞
−
⎛
⎜⎟
+
⎝⎠
⎞
x
;
17)
ln(2 )]lim 2 [ln( 1)
x
x
→∞
+ x− +
; 18)
2
tg 2
/4
lim (sin 2 )
x
x
x
π
→
;
()
2
1
2
0
lim 1 tg
x
x
x
→
+
; 20)
m( 3tg )
2
2ctg
0
li 1
x
x
x
→
+
; 19)
()
2
ctg
0
lim cos
x
x
x
→
21) ; 22)
(
)
tg2
/4
lim tg
x
x
x
π
→
;
23)
1
0
lim( )
x
x
x
x
e
→
+
; 24)
tg
/2
lim ctg
2
x
x
x
π
→
⎛⎞
⎜⎟
.
⎝⎠
23
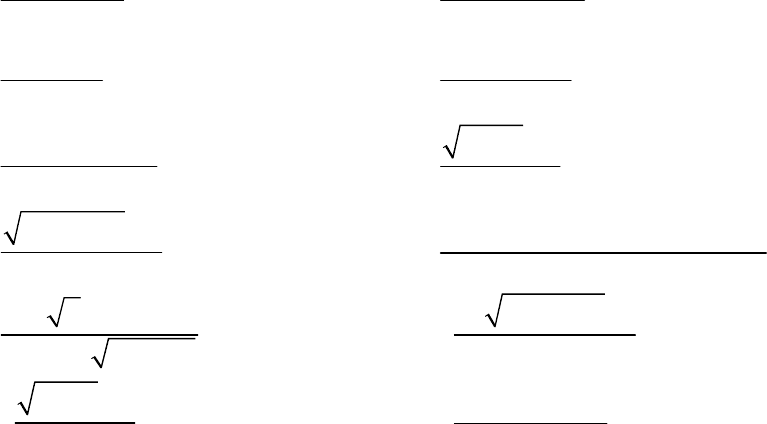
3.31. С помощью принципа замены эквивалентных вычислить пределы:
1)
0
ln(1 3 )
x
1cos
lim ;
x
x
x
→
−
−
2)
sin 3
0
1
x
ln sin 4
lim ;
x
(1 )
x
e
→
+
−
3)
0
arctg4
lim ;
arcsin 2
x
x
x
→
4)
sin 5
0
1
lim ;
ln(1 tg2 )
x
x
e
x
→
−
+
5)
2
0
ln(2 cos 4 )
lim ;
2 )ln (1 sin
x
x
x
→
−
+
6)
2
4
0
11
lim ;
coln s
x
x
x
→
+
−
2
0
11
lim ;
lcos3
x
xx
x
→
++ −
−
8)
22
0
sin 2 arcsin 4 arctg 5
lim ;
7)
31cos2
x
x
xx
x
→
+−
x+−
2
0
ln(1
1cos
lim ;
arctg2 )
x
x
x
x
→
−
+
3
2
3
0
sin ln(1 4 )
lim
9)
;
(1)arcsin
x
x
x
x
e
→
+
− x
10)
2
4
0
11
lim
(1
x
x
x
xe
→
+−
−
)
; 12)
2
2
0
ln
li
11)
(1 )
m
(1 4 )
x
x
x
xx
→
+
+
−
.
НЕПРЕРЫВНОСТЬ ФУНКЦИИ.
ТОЧКИ РАЗРЫВА И ИХ КЛАССИФИКАЦИЯ
Функция
ТЕМА 4
()
f
x называется непрерывной в точке
0
x
, если
lim ( ) ( )
x
0
0
x
f
xfx
=
.
→
()
f
x непрерывна в точке
0
x
Функция тогда и только тогда, когда
00
lim ( ) lim ( ) li ( ) ( )
x
000
0
x xx xx
m
f
xfxfxfx
−
===
.
ункция
→ →+ →
Ф ()
f
x непрерывна на множестве , если она непрерывна в ка-
ждой точке этого множества.
X
Функция ()
f
x называется непрерывной в точке
0
x
слева (справа), если
im
()
0
00
0
l ( ) ( ) lim ( ) ( )
x xx
0
0
x
f
xfx fxfx
→ →+
==
.
−
Если в точке
0
x
функция не является непрерывной, то говорят, что она
имеет разрыв в точке
0
x
и точка
0
x
называется точкой разрыва.
Точка
0
x
называется точкой разрыва первого рода функции ()
f
x , если
пределы слева и справа
0
0
lim (
xx
(
)
f
x
→+
и
0
0
lim ( )
xx
f
x
→−
) конечны. Если при
этом
24

0
0
00
lim ( ) lim ( ) ( )
xx xx
0
f
xfxfx
→− →+
=≠
,
0
x
то – точка устранимого разрыва; если же
00
00
lim ( ) lim ( )
xx xx
f
xf
→− →+
≠ x
,
о
0
x
– точка неустранимого разрыва первого рода. В этом случае разность т
00
00
lim ( ) lim ( )
xx xx
f
xf
→+ →−
−
x
называется скачком функции ()
f
x в точке
0
x
.
Если хотя бы один из пределов
0
0
li
xx
m ( )
f
x
→−
,
0
0
lim
xx
( )
f
x
и
lim ( )
→+
0
xx
f
x
не суще-
ствует или бесконече
→
н, то точка
0
x
называется точ разрыва кой второго рода
функции ()
f
x.
мер 3.24. Даны функции:
Примеры решения задач
При
1)
1
()
2
fx
x
=
−
;
2
() 2, 4 2,
,2.
fx x x
xx
2
,4xx
⎧
−≤−
⎪
2)
=
−<<
⎨
⎪
≥
⎩
ти точки а сследовать их характе Определить скачки
функц в точках, гд зрывы первого рода.
Решение. 1) Функция
Най разрыв и и р.
ии е имеются ра
1
2x
y =
−
определена и непрерывна при всех значе-
ниях переменной (;2)(2;)
x
∈−∞ +∞∪ . Поэтому разрыв может быть только в
точке
2
x
=
.
рактера Для исследования ха разрыва найдем односторонние пределы
функции в точке
2
x
=
:
20
lim
2
x
x
→−
=−∞
−
,
1
20
lim
2
x
x
→+
1
=
+∞
−
.
2
x
=
Так как односторонние пределы равны бесконечности, то точка –
точка разрыва второго рода.
2) Область определения функции – вся числовая ось ). На интер-
валах
(;−∞ +∞
(;4)(4;2)(2;)
x
∈−∞− − +∞∪∪ функция непрерывна. Поэтому разры о-
гут быть только в точках
вы м
4
x
=−
и
2
x
=
, в которых меняется аналитическое за-
дание
односторонние пред
функции.
Найдем елы в точке
4
x
=
−
:
2
(4 0) ) 6fx−− =
,
(4 0) lim2 8fx
40
lim( 1
x→− −
− =−
x→− +40
−
+= =−
.
25
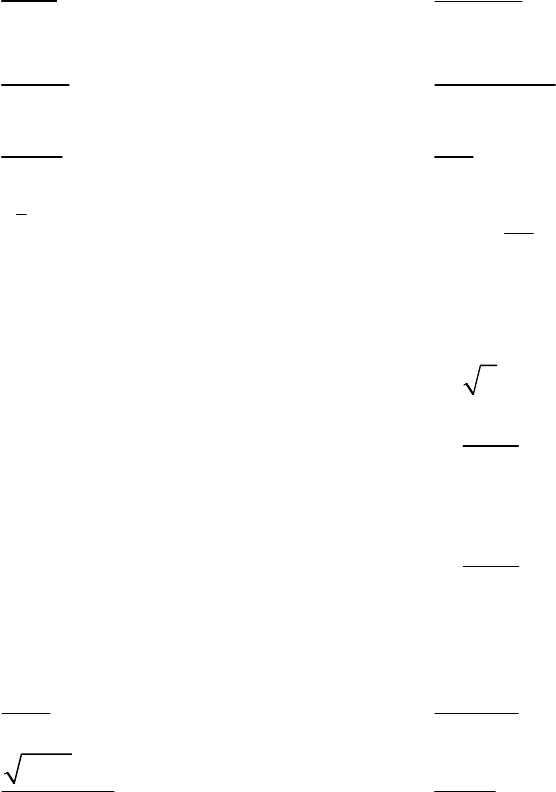
Значение функции в точке
4
x
=
−
определяется первым аналитическим вы-
ражением, т.е.
. Так как
2
( 4) ( 4) 16f −=−− =
(4 0) (4 0)
f
f
−
−≠−+ и указанные
пределы конечны, то
4
x
=
−
– точ странимого разрыва первого рода. Скачок
функции в точк (4 0) 8
ка неу
е равен (4 0) 8 (16)разрыва
f
f
−
+− =. Заметим,
что (4 0) (4)
−−=−−−
f
f−− = − вательно, в точке
4
, следо
x
=
−
функция непрерывна слева.
Рассмотрим точку
2
x
=
:
) lim 2 4= =
,
2
(2 lim 4fx
fx
→−
− 0)
x→+
20
(2 0
x
20
+
=
е функции в точке
=
.
x
Значени 2
=
определяется третьи аналитическим
выражением, т.е.
м
2
(2) 2 4f
=
=
. Так как
(2 0) (2 0) (2)
f
ff−= +=
то в точке
2
,
x
= ф ерывна. ункция непр
Задания для самостоятельного решения
3.32. Исследовать характер точек
:
на непрерывнос ь функции и установитьт
разрыва
1)
1
y
5
x
= ; 2)
()
3
1
y =
;
−
3x +
2
1
4
y
x
=
−
3)
; 4)
2
1
56
y
xx
=
−
+
;
2
3
x
y =
−
5)
1
; 6)
tg
x
y
x
= ;
7)
1
4
x
y =+
2
1
1
; 8)
arcsiny
x
= ;
9) cos , 0 / 2,
0, / 2;
x
yxx
x
−
⎧
⎪
=<<π
⎨
⎪
≥π
⎩
10)
1, 1,
0, 1 0,
,0;
xx
yx
xx
⎧
−−
2, 0,
x
≤
<−
⎪
=
−≤ <
⎨
⎪
≥
⎩
11)
,
12)
2
1, 2,
5, 2 5
2, 5;
xx x
yx x
x
⎧
−+ <
⎪
=− <<
⎨
⎪
≥
⎩
2
1
,3,
3
,3
36
,6.
5
x
x
yx x
x
x
⎧
<
⎪
−
⎪
⎪
6,
=
≤<
⎨
⎪
⎪
≥
−
⎪
⎩
3.33. Доопределить (если это возможно) функции так, чтобы они стали
непрерывными:
1)
sin
x
y
x
= ; 2)
2
4
x
x
y
x
+
= ;
3)
12
1
x +
+
; 4)
1
x
e
y
x
−
= .
y
x
−
=
26
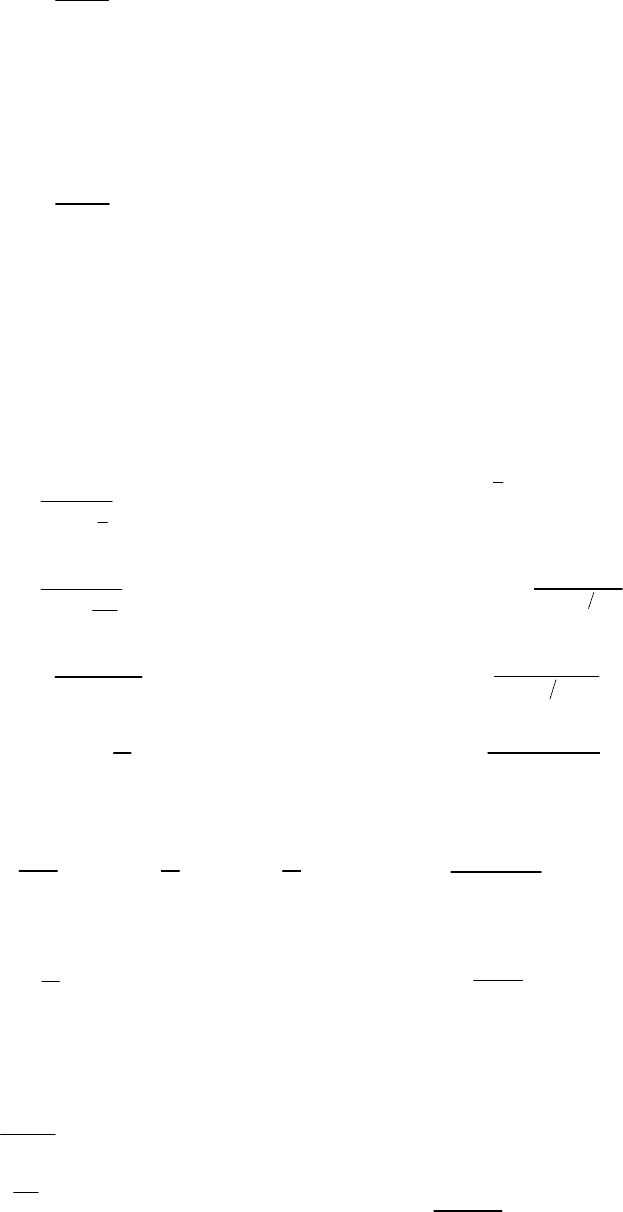
()yfx
=
в точке
x
a
=
3.34. Найти односторонние пределы функции . Ис-
следовать функцию на непрерывность:
1)
2
2, 0,
() 0, 1;
4, 0,
xx
fx a a
xx
−
>
⎧
===
⎨
−≤
⎩
sin
,0,
() 0;
cos , 0,
x
x
fx a
x
xx
⎧
≥
⎪
==
⎨
⎪
<
⎩
2)
3)
=
4)
1, 0,
() 0, 1;
1, 0,
xx
fx a a
xx
+>
⎧
==
⎨
−≤
⎩
sin
,0,
||
() 0, ;
1, 0,
x
x
x
fx a a
x
π
⎧
≠
⎪
==
⎨
⎪
=
⎩
=
5)
=
,0,
() 0, 1;
5, 0,
x
ex
fx a a
xx
⎧
<
==
⎨
+≥
⎩
6)
1, 0,
() 0, 1;
2, 0,
x
xx
fx a a
x
+
<
⎧
==
⎨
≥
⎩
=
7)
1
1
() , 0;
22
x
fx a==
−
8)
1
() , 0;
x
fx e a
=
=
9)
1
1
1
() , 0;
10)
11
1
() 2 , 1
13
x
f
xa
−
+=
+
;
=
14
x
fx a
−
==
−
3
4
() ,
11)
2;
12)
(2)
fx a
x
==±
−
()
13
1
() , 3;
12
x
fx a
−
=
=±
+
13)
1
( ) arctg , 0;fx a
x
==± 14)
log(2 )
() , 2 0fx
2
x
a
x
−
=
=−
−
.
3.35. При каком значении
A
функция является непрерывной в точке
0x
0
=
:
tg
,;00;,
44
x
y
x
∈−
⎪
⎜⎟ ⎟
=
⎝⎠ ⎠
⎨
∪
2)
,0;
x
Ax
⎧π
⎛⎞⎛⎞
⎜
⎝
⎪
=
⎩
π
()
,1;1,x
y
x
∈−
⎪
=
⎨
1)
ln( 1)
,0;
x
Ax
+
⎧
⎪
=
⎩
3)
2
1
,0
,0
x
ex
y
Ax
−
⎧
⎪
≠
=
⎨
⎪
=
⎩
,
;
4)
2
1
|4|
,0
,0
xx
ex
y
Ax
−
−
⎧
⎪
≠
=
⎨
⎪
=
⎩
,
?
. Исследовать на образить графически функции:
1)
3.36 непрерывность и из
2
5
y
x
= ; 2 2
−
) y|x |
=
− ;
3)
3
1
5
x
y
−
=
; 4)
sin 2
x
y
x
= .
27
Задания для индивидуальной работы № 8
Задание 8.1.
Таблица 8.1
Н
ва
Вычислить предел функции (см. табл. 8.1):
омер Номер
рианта варианта
1
2
2
1
23
lim
2
x
1
x
x
xx
→
−+
+−
16
2
2
1
2
lim
43
x
xx
xx
→−
−−
++
2
2
2
2
25
lim
32
x
xx
xx
→
−+
−+
2
17
2
2
2
32
lim
23
x
xx
xx
→−
++
+−
2
3
2
2
1
34
lim
32
x
1
x
x
xx
→
−+
−+
18
2
2
12
23
lim
23
x
1
2
x
x
xx
→
−+
+−
4
2
2
3
23
lim
43
x
xx
xx
→
−−
−+
19
2
2
4
3
lim
6
x
xx
xx
→
−−
−+
4
8
5
2
2
3
23
lim
43
x
xx
xx
→
−−
−+
20
2
2
1
34
lim
2
x
xx
xx
→
+−
+−
6
2
2
1
2
lim
32
x
xx
xx
→−
−−
++
21
2
2
1
32
lim
21
x
xx
x
x
→−
++
+−
7
2
2
2
35
lim
2
x
xx
xx
→−
+−
+−
2
22
2
2
13
32
lim
37
1
x
xx
xx
→
+−
−+
2
8
2
2
2
35
lim
2
x
xx
xx
→−
+−
+−
2
23
2
2
3
23
lim
43
x
xx
xx
→−
+−
++
9
2
2
2
32
lim
35
x
xx
xx
→−
++
+−
2
24
2
2
1
2
lim
34
x
xx
xx
→−
−−
−−
10
2
2
2
2
lim
32
x
xx
xx
→−
+−
++
25
2
2
2
32
lim
37
x
xx
xx
→
−+
−+
2
11
2
2
1
2
lim
1
x
xx
x
→
+−
−
26
2
2
1
21
lim
32
x
xx
1
x
x
→−
+−
+−
12
2
2
13
34
lim
35
x
1
2
x
x
xx
→
−+
+−
27
2
2
12
23
lim
23
x
xx2
1
x
x
→
+−
−+
13
2
2
13
34
lim
37
x
xx
xx
→
−+
−+
1
2
28
2
2
1
34
lim
43
x
1
x
x
xx
→
−+
−+
14
2
2
1
2
lim
43
x
xx
xx
→
+−
−+
29
2
2
1
2
lim
32
x
xx
xx
→
+−
−+
15
2
2
1
34
lim
21
x
xx
x
x
→−
−−
+−
30
2
2
3
23
lim
43
x
xx
xx
→−
+−
++
28

Задание 8.2. Вычислить пределы функций (см. табл. 8.2):
Таблица 8.2
Н
варианта
омер
1
32
4
23
lim
22
x
xx
xx
→∞
++
−+
1
(
)
22
lim 2 1 3
x
хх хх
→±∞
+
−− −+
2
85
8
743
lim
5
x
xx
х
x
→∞
+−
−
(
)
22
lim 5 1 3 4
x
хх хх
→±∞
+
−− − +
3
43
42
24
lim
33
x
xx
х
xx
→∞
−+
++
(
)
22
lim 2 4 3 2 1
x
хх хх
→±∞
−+− −+
4
53
2
743
lim
273
x
xx
х
xx
→∞
+−
++
(
)
22
lim 3 5
x
хх хх
→±∞
+
+− −+
5
2
2
91
lim
56
x
x
xx
→∞
+
+−
3
(
)
22
lim 5 10 2
x
х
хх
→±∞
+− −
6
2
2
72
lim
3
x
xx3
x
x
→∞
−−
−
(
)
22
lim 2 3 4
x
ххх
→±∞
+
−−+
7
32
2
2
lim
7
x
xx
x
→∞
−−
−
(
)
22
lim 2 2 3 1
x
хх х х
→±∞
−− + −
8
53
7
423
lim
35
x
х x
xx
→∞
−+
+−
(
)
22
lim 3 1 3
x
хх хх
→±∞
−
+− −+
9
42
5
3
lim
6
x
x
x
x
x
→∞
+
−
(
)
22
lim 4 3 3 4
x
хх хх
→±∞
−
−− + +
10
32
3
32
lim
1
x
xx
х
x
→∞
+−
−
(
)
22
lim 3 3 1 2
x
х
хх
→±∞
−+− −
х
11
2
3
43
lim
5
x
x
x
x
→∞
+
+
(
)
22
lim 3 2 4
x
ххх
→±∞
−
−−+
12
73
53
64
lim
32
x
7
x
x
xx
→∞
+
−+
22
lim 3 2 3
x
х
хх
→±∞
+
−−
13
2
2
47
lim
25
x
x
1
x
x
→∞
+
−+
(
)
22
lim 5 2 5
x
ххх
→±∞
+
−−+
14
2
2
25
lim
32
x
1
x
x
xx
→∞
+−
+−
(
)
22
lim 2 2 3 3
x
хх хх
→±∞
−+− +−
15
2
3
1
lim
32
x
x
xx
→∞
−
+−9
(
)
22
lim 7 3 4
x
хххх
→±∞
+
−−+
16
3
2
21
lim
53
x
x
x
xx
→∞
−+
++
(
)
22
lim 5 3 2
x
х
хх
→±∞
−+− +
х
29
Окончание табл. 8.2
17
52
6
73
lim
23
x
xx
xx
→∞
++
+−
2
(
)
22
lim 2 3 1
x
хх хх
→±∞
−
+− −−
18
2
2
62
lim
35
x
1
1
x
x
xx
→∞
+−
−+
(
)
22
lim 7
x
5 2
х
ххх−− +
→±∞
+
19
3
2
34
lim
24
x
xx
xx
→∞
+−
+−
(
)
22
lim 7 3 2
x
х
хх
→±∞
++− −
х
20
42
2
725
lim
731
x
xx
xx
→∞
++
−+
(
)
22
lim 5 3 5 3
x
хх хх
→±∞
+
+− − −
21
32
2
4321
lim
3
x
xx
х
x
→∞
+−+
−
(
)
22
lim 2 3 2 2 5
x
хх хх
→±∞
+
−− − +
22
75
97
19 3 2
lim
872
x
xx
3
5
х
xx
х
→∞
−+
+−
(
)
22
lim 2 3 2
x
х
хх
→±∞
+−− +
х
23
2
2
33
lim
22
x
x
x
→∞
−
+
(
)
22
lim 2 1 1
x
х x х
→±∞
+
−− +
24
2
21
lim
3
x
x
x
x
→∞
++
−
(
)
22
lim 2 3 2 4
x
хх хх
→±∞
−
+− + +
25
3
2
45
lim
37
x
x
x
→∞
+
+
(
)
22
lim 2 2 2 3 1
x
хх хх
→±∞
+
−−+
26
3
4
523
lim
726
x
xx
xx
→∞
+−
−+
(
)
22
lim 2 1 2 3
x
хх хх
→±∞
+
−− + +
27
73
82
93
lim
43
x
xx
xx
→∞
++
−+
3
2
22
lim 1 1
x
х
ххх
→±∞
+
+− −−
28
2
4
lim
4
x
x
x
→∞
+
−
(
)
22
lim 2 1 3
x
хх хх
→±∞
+
−− −+
29
2
2
2
23
lim
32
x
xx
xx
→
++
++
1
4
(
)
22
lim 3 2 3 3
x
хх х
→±∞
+
−+
30
2
3
3
1
lim
1
x
x
x
→−
+
−
(
)
22
lim 5 3 2
x
х
хх
→±∞
−+− −
х
Задание 8.3. Вычислить предел функции (см. табл. 8.3):
Таблица 8.3
Номер
варианта
Номер
варианта
16
1
0
sin 3
lim
2
x
x
0
4
lim
sin8
x
x
x
→
x
→
17
0
1co
2
0
7
lim
arcsin 5
x
x
x
→
s2
lim
x
x
x
→
−
30
