Румянцев Н.В., Медведева М.И., Полшков Ю.Н., Пелашенко А.В. Практикум по решению задач курса Высшая математика
Подождите немного. Документ загружается.

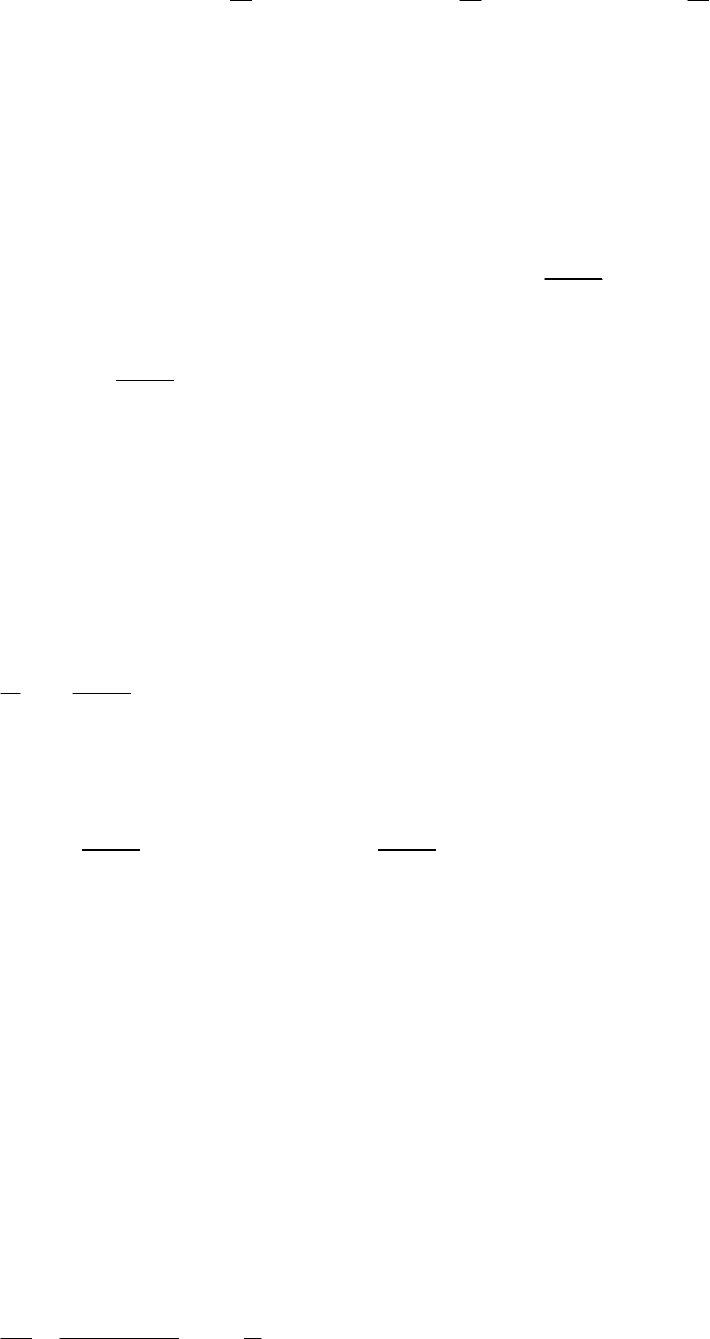
(20) 2
cos 20 40 cos 19 380cos 18
222
yx x xx x
π
⎛⎞ ⎛ ⎛⎞
=++ ++ +=
⎜⎟ ⎜⎟ ⎜⎟
⎝⎠ ⎝ ⎝⎠
ππ
⎞
⎠
380)cos 40 sin
2
(
x
xxx=− +
.
и производную функции
cos
x
yx=
Пример 4.9. Найт .
Решение. Первый способ. Так как
cos
ln cos ln
x
x
xx
ye e
⋅
==
, то
()
cos ln cos ln
cos
cos ln sin ln
xx xx
x
ye x x e x x
x
⋅⋅
⎛⎞
′
′
=⋅⋅= −⋅+
⎜⎟
⎝⎠
=
cos
cos
sin ln
x
x
x
xx
x
⎛⎞
=−
x y xx=⇒=
.
по переменной
⋅
⎜⎟
⎝⎠
.
Второй способ. Рассмотрим логарифм заданной функции:
cos
ln ln ln cos ln
x
y
Дифференцируя обе части
x
и считая, что функция
yx является сложной функцией, получаем
ln ( )
1cos
sin ln
x
yx
yx
′
x
=
−⋅.
Следовательно,
cos
cos cos
sin ln sin ln
x
x
yy
x
x
⎛⎞⎛⎞
−
⎟
⎠
.
x x x x
xx
′
=−⋅= ⋅
⎜⎟⎜
⎝⎠⎝
Пример 4.10. Для функции
5( sin ),
x
tt=−
⎧
5(1 cos ),yt
⎨
⎩
заданной параметрически, найти производную первого порядка от по пере-
менно
=−
y
й
x
.
Решение. Находим производные от
и
y
x
по переменной :
t
5(1 cos ); 5sin
tt
x
ty t
′′
=− =
.
из (4.4) следует, что
Тогда
5sin
ctg (
t
t
=≠
2 , 0, 1, 2,...)
5(1 cos 2
dy t
kk
dx
π
= =±±
−
.
)t
41
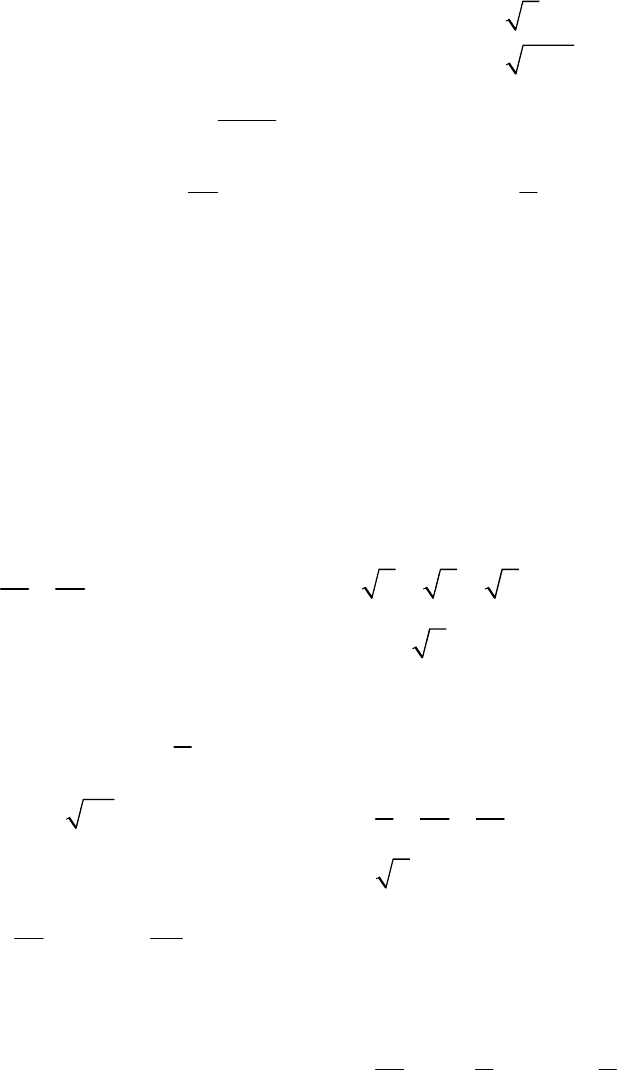
ешения
. Найти приращ
Задания для самостоятельного р
4.1 ение функции
yx
2
2
=
+
в точке
1
x
=
при:
2)
1)
0,01;
x
∆= 0,3
x
∆=−
.
4.2 ращение функции
yx
. Найти при
x
2
=
−
в точке
0
x
=
при:
2)
1)
0,001;
x
∆=
x
∆=0,5−
.
4.3 пр из. Пользуясь определением о водной, найти производную функции
в каждой точке ее области определения, если;
; 1) 2) cos 2yx= ;
3
yx=
3)
,0yxx
=
>
;
x= ; 4) y 5)
23
yx x=+
;
sin 4
6)
1, 1yx x
=
−>
;
x=+
; 8)
3
2
1
2
y
x
9)
2
logyx
=
7)
y
= ;
;
+
10)
3
x
y =
; 11)
2
1
x
1
1y
x
=
+; 12) .
Пользуясь определением производную функции в заданной
точке
4.4. , найти
0
x
:
1)
y
2)
yx
0
2, 1;xx=− =
x
2
0
2, 0;
=
+=
,x x=−
2 , / 4;xx
3)
0
1;y x=
4)
siny
2
0
=
π
=
5)
0
cos , / 2;yxx
π
==
6)
0
2, 1;
x
yx
=
=
0
ctg , / 4;yxx
π
==
0
4
,0,
0.
,0,
x
yx
xx
≥
8)
2
x
⎧
⎪
7)
=
=
⎨
Найти прои кций:
−<
⎪
⎩
4.5. зводные следующих фун
34
2
;
34
xx
y 2) x=−+
1)
3
4
;y=xxx−+
3)
4)
2
(1 2 ) ;yx=+
3
()yx x=+
;
234 35
x
xxxx
y
−
+⋅
; 6)
lnyx
=+−
log 2logx x
=
5)
23
+−
;
1
sin 4cosyx x
x
=+ − x x; 8) y
7)
tg 3ctg+ ;
=
9)
5
42yx x=−
; 10)
23
11 1
y
x
xx
=
−−;
x
;
11)
12)
2
5log3
x
y=−
5
cos(3 1) tg3yx x=− ++x
;
2
ln 4
42
x
x
yx
1
x
=+ −;
+
;
yx=−
;
14)
=
50
(1 2 )yx
13)
15)
cos
x
ex
; 16)
=arcsin sin
x
ye x
17)
2
arcsin 3yx x=
; 18)
5
22
5
yx x
xx x
=+−−
11 1
⎛⎞
⎛⎞⎛⎞
⎜⎟
⎜⎟⎜⎟
⎜⎟
⎝⎠⎝⎠
⎝⎠
;
42
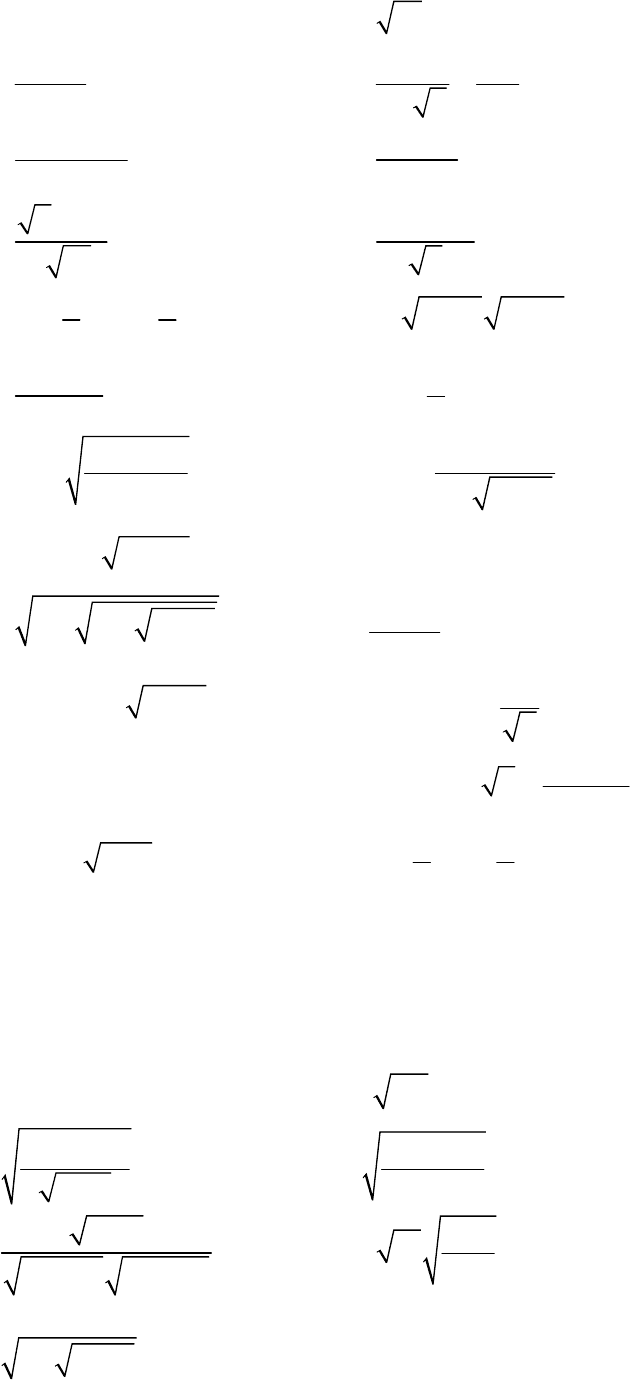
19)
2
) ln(1 )x x+ −
; 20)
2y=
(1y= x
;
yx=
arccos 2
x
21)
)cos(31)x x+ −
; 22)
2
(
2
5
y
3
log ( 1)x x
=
−
;
2
2
ln
1
x
x
y
x
=
+
23)
; 24)
2
1
3
1
3
1
x
x
y
x
+
=+
−
;
25)
tg ctg
tg ctg
x
x
y
x
x
−
=
+
; 26)
2
arctg
2
x
x
y
x
=
+
;
27)
sin
4
x
x
x
y =
; 28)
2
(1 2 )
x
y
x
+
=
;
x
29)
22
2
2
sin cos
x
y
x
=+
22
ln 1 1
; 30)
yxx
=
−+
;
31)
x
x
x
x
ee
y
ee
−
−
−
=
+
; 32)
ln tg cos ln tg
2
x
yx=− x
;
33)
2
log
1sin2
1sin2
x
y
x
−
=
+
; 34)
2
arctg
11
y
x
x
=
+
−
;
(
)
2
ln 1
x
x
ye e=++
; 36)
x
e
x
e
xe
ye e e
⎛⎞
⎜⎟
⎝⎠
=+ +
35)
;
37)
3
3
2
3
1yxx x=+++
; 38)
6
6
12
arcctg
1
x
yx
x
=− ;
+
39)
(
)
2
g 1 x+
; 40)
2
2
1
ln arccos
x
x
ye
x
−
e
⎞
=+
⎟
⎝⎠
;
⎛
⎜
arctyx=+
41)
2
9
log ( 1)
3
xx
y
++
=
; 42);
2
2
1
arcsinyx x
cos
x
x
=+
11
ln ln lnyx
xx
⎛⎞
⎛⎞
=++
⎜⎟
⎜⎟
⎝⎠
⎝⎠
43)
2
sin
arcsin 1 5
x
yx=++; 44) .
4.6. Пользуясь логарифмическим дифференцированием, найти производ-
ные следующих функций:
1)
1/
x
yx=
; 2)
2
2
log 2 log ( 1)
x
x
yx
=
++
;
3)
cos
x
yx=
; 4)
x
x
yx=
;
s )
(
)
1
tg
x
yx
+
=
sin
5)
(co
x
yx
; 6)
=
;
7)
32
(1)xx
8)
3
sin 2
1sin2
x
+
y
x
=
−
;
3
5
5
y
x
=
;
−
9)
2
3
2x
+
=
3
)
y
; 10)
323
7
4
1
(2),
1
1yx x xx
−x
x
(1)( 4
xx
−+
=
+>
+
.
. иффер цируемость функции: 4.7 Исследовать на д ен
2
11=−−; yx 2) | | sinyx x
=
; 1)
43
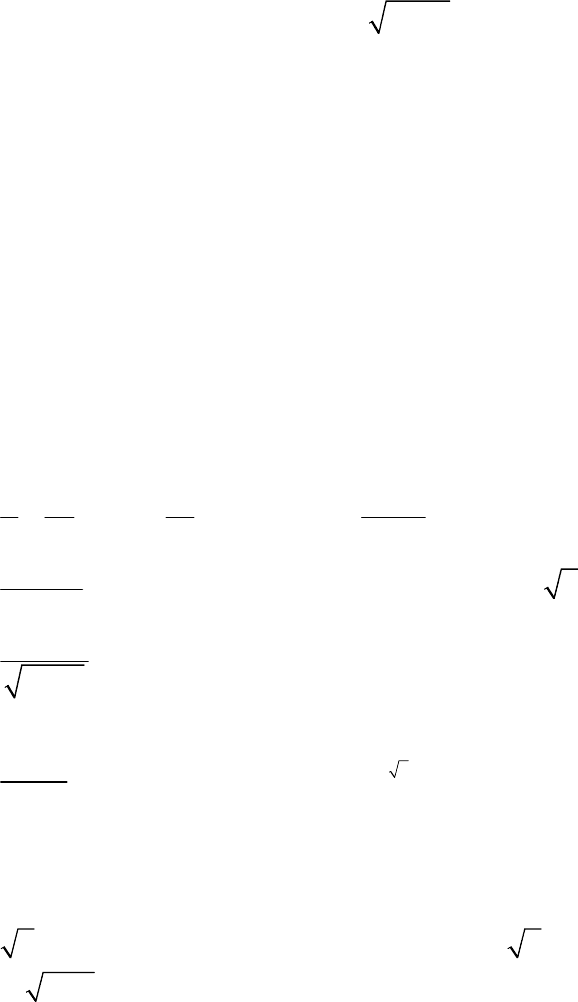
3) | sin |x x= ; 4y ) ;
x
≥
⎧
2
||yxx=
5)
2
,0,xx
y
⎧
>
⎪
= ;
=
4
,0;xx
⎨
≤
⎪
⎩
6)
2
,0.
y
xx
⎨
0, 0,
<
⎩
4.8. Найти правую и
0
x
левую производные в точке :
2)
1)
|1|, 1x x=+ =−
;
0
y
2
0
1, 2yx x
=
−=
;
=
4)
,
0;
s , 0,
ex
yx
xx
⎧
≥
3)
=
⎨
<
⎩
co
0
,0,
0;
5, 0,
xx
yx
xx
≥
⎧
,0
x
0
=
=
⎨
<
⎩
5)
|sin |,yxx
0
π
==
; 6)
0
||| 1|, 0yx x x
=
−+ =
;
7)
|,1x =
8)
2
0
|yx x=−
;
2
0
sin sy in ,xxx
π
=
−=
;
0
tg ctg , / 4yxxx
π
==
9)
; 10)
0
arcsin(sin ), / 2yxx
π
=
=
.
. брать коэфф енты ак, чтобы функция4.9 Подо ици
a
и
b
т ()
f
x была не-
прерывной и диффе моренцируе й в точке
0
x
x
=
, е и сл
0.
, ,
bx
x x
x
e xx
−
+ ≥
1)
0
2)
)
()
bx
fx
xa
⎪
2
,,
2
ax
⎧
+
0
()
,;
xxx
fx
ax b x x
⎧
≤
=
⎨
+>
⎩
0
0
0
1, ,
(
=
=
+<
⎪
⎩
я Лейбница, производные указанных по-
рядко я функций:
20)
1),найти
x
y+
;
cos , наyx x=
;
(2 1)syx=−
.
1. Найти производны рядка следующих функций:
⎨
4.10. формулу
в дл
Применя найти
1)
2(25)
sin , найтиyx x y=
; 2)
(y у x=
2(
3)
10)
йти y
; 4)
3(
(5)
cos , найти
x
ye x y
−
=
5)
6)
in , найтиx y
; 6)
2( (10)
(1 ) sin , найти
x
yex y
−
=−
4.1 е второго по
2
1
3
x
y
x
+
=
+
2
2
1)
3
13 5
5yx
x
x
=− − +
x
; 2)
;
cos3
2ln
x
y
x
=
−
; 4)
(
)
siny=
3)
2 cos5xxx+ ;
5)
2
arcsin
1
x
y
x
=
−
; 6)
2
x
ye
−
=
;
7)
3arcsin2
x
yx=
; 8)
3
cos 2yx x
;
=
9)
3
y
sin 3
x
= ; 10)
5
x
y =
;
tg5
5
x
ye=
; 12)
3
ln ( 1)yx
=
+
11)
.
4.12. Пользуясь правилом дифференцирования обратной функции, найти
указанные производные:
1)
4
, найти
x
yx y
′
=
; 2)
arccos , найти
x
yxy
′
=
;
3)
ln 1 , найти
x
yx y
′
=+
;
32
23,найти
y
x x x
′
=+
;
5)
cos 2 , найтиyxx
=+
3)
y
x
′′
; 6) .
4.13. Для ункций, заданных параметрически, найти указанные производные:
yy
22
, найти
x
yy
yx e x
′′
=+
ф
44

1)
n sin55si
x
tt
, 5cos cos5ytt, найти
x
y
′
=
−
=+
;
2)
2
,
t
x
e=
2t
ye
−
=
, найти
x
y
′
;
3)
3
2cos ,
x
t=
3
2sinyt=
, найти
x
x
y
′
′
;
4)
cos ,
t
x
et=
sin
t
ye t=
, найти
x
x
y
′
′
;
5)
3
yt
=
, найти
x
xx
y
′
′′
,
t
x
e
−
=
;
6) arcsin ,
x
t=
2
1yt
=
−
, найти
x
x
y
′
′
;
7)
2
3,xt=−
3
yt t
=
−
, найти
x
x
y
′
′
;
8)
x
y
′
2
ln(1 ),
x
t=+
arctgyt t
=
−
, найти .
.14. Для неявно заданных функций найти4
x
y
′
:
1)
22
0xxyy++=
; 2)
32
4530xy x y
−
−+ =
;
−
3)
ln
x
5
y
x
e
−
+=; 4) 20xy x y
+
+−=;
)
22
arctg ln
y
x
y
5
x
⎛⎞
=
+
⎜⎟
; 6)
sin cos 0
yx
exe y
+
=
⎝⎠
;
)
;
y
2
arctg 0yyx−+ =
8)
xy
exe
+
=+
7
;
9)
x
y
x
ye
+
−=
; 10)
e
y
exy
+
=
.
сли приращение функции
ТЕМА 2
ДИФФЕРЕНЦИАЛ ФУНКЦИИ
y
∆
Е может быть представлено в виде:
x( ) () () (, )yfx x fx Axx xx
α
∆= +∆ − = ∆+ ∆∆,
е
гд
0
lim ( , ) 0
x
xx
α
∆→
∆=
, то функция ()yfx
=
называется дифференцируемой в точке
x
. Главная линейная часть ()
A
xx
∆
называется ифференциалом функции и
обозначается или . Дифференциал функции существует тогда и только
тогда, когда существует конечная производная
д
()df x dy
()yAx
′
=
. Дифференциал функ-
ции м записать с :
Если
ожно ледующим образом
()yydx xdx
′′
∆= =
.
f
x
∆
достаточно мало, т стью до бесконечно малых более
высокого порядка, чем
о с точно
x
∆
, справед лиженная формула . Кро-
ме того, из (4.5) следует, что
лива приб ydy∆≈
x
x
∆
= .
последовательно определяются по
форму
1
dy dy ddy dy dd y
−
= =
Дифференциалы высоких порядков
лам:
2
dy d=
.
32
( ), ( ),..., ( )
nn
45
Примеры решения задач
Пример 4.11. Найти дифференциал функции
x
.
Вычислить при
2
ln( 3 3) sin 2у xx=+++
dy
0
x
=
,
0,01
x
∆=
.
Решение.
()
2
ln( 3 3) sin 2x x dx
′
+
2
23
2 cos 2
33
x
dy x x dx
xx
+
⎛⎞
=+ + = +
⎜⎟
++
⎝⎠
.
Подставив
0
x
=
и
0,01dx x=∆ =
, находим
(
)
1 2 0,01 0,03dy =+⋅ =
.
дифференциал функции
yx=−
Пример 4.12. Найти приращение и
2
5x
в е
1
32+
точк
x
=
пр
1
и
0,
x
∆
=
. Найт
шности, ются при замене
и абсолютную и относительную
погре которые допуска приращения функции ее диф-
ференциалом.
xx x x− +∆ + − − + =
Решение. По определению
22
()()3()yyxxyx xx∆ = +∆ − = +∆ 2()5(325)
2
36 2
x
xx x=∆ + ∆−∆
и
(6 2)x x
′
=−∆
.
( ) (6 2)dy y x dx x dx==−
Тогда
2
3626 2ydy x xx x∆− =∆ + − − +
2
x x x x∆ ∆ ∆ ∆=∆
.
При
3
1
x
=
и
0,1
x
∆=
получаем 0,4y , 0,4dy
=
, 0,03ydy
∆
−=3
∆
= . Следо-
ательно, абсолютная погрешность ||0,03ydyв
, относительная
∆
−= погрешность
0,03
0,07 или 7%.
0,43
ydy
y
∆−
=≈
∆
При иближенно .
ешение
. Так как yyx∆= +∆
мер 4.13. Найти пр sin 29
Р
()()x yx− и ydy
∆
≈ , то ()()yx x yx dy+∆ ≈ + .
Пусть sinyx= , 30
x
=
и 1
x
∆=−. Тогда
3
cos cos30
180 360
π
π
⎛⎞
dy xdx==⋅−=−
⎜⎟
⎝⎠
и
13
sin 29 sin(30 1 )
π
=−−=
0,485
2360
≈
.
46
Задания для самостоятельного решения
.15. Найти дифференциалы от функций:
1)
4
2
2
1
yx
x
=+; 2)
2
1
x
y
x
x
+
= 3) ln cos2yx=− ;x
функций
;
+
4)
2
cos 3 1yxx=−+
; 5)
arcsin 2
x
ye x=
; 6)
5cos3
x
yx=
.
.16. Найти дифференциалы и значения дифференциалов4 ()yfx
=
:
1)
yx=
3
2
. Найти
sin
0,1
(), ( /8), ( /8)
dx
df x df df
π
π
=
;
2)
. Найти
2
ln(1 )yx=+
0,01
(),(2),(2)
dx
df x df df
=
.
4.17. Най
1)
ти дифференциалы второго порядка:
2
2
x
y
−
= ; 2)
2
1yx
=
−
;
x
;
5)
3)
2
lnyx=+
4)
2
sin ( 1)yx=+
; ln(cos )yx
−
; 6)
3
5yx=+
.
4.18. Найти приращение и дифференциал функции
2yx=+
при
2
x
=
и
0,01
x
∆=
. Вычислить абсолютную и относительную погрешности, которые
допускаются при замене пр ом.
4.19. Найти приращение
иращения ее дифференциал
y
∆
и дифференциал функции dy
2
arctg
x
ye=
при
0
x
=
и
0,02
x
∆=
. Вычислить абсолютную и относительную погрешности,
сякоторые допускают при замене приращения ее дифференциалом.
иближенно: 4.20. Вычислить пр
1)
3
27,01
; 2) 3) ;
) ;
lg10,03;
arccos 0,01
sin 44 57
′
° ; 6)
5
33
4 tg31° 5)
.
ТЕМА 3
ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ
Касательная
функции
Уравнение касательной к графику дифференцируемой ()yfx
=
в точке
000
(, )
M
xy
, где
00
()yyx=
, имеет вид
00
()( )yy yxxx
′
0
= −
. (4.6)
−
Углом между двумя кривыми ()yfx
=
и y ()gx
=
в точке их пересечения
называется угол между двумя касательными к их графикам в этой точке
нение нормали в точке
000
(, )
.
Урав
M
xy
имеет вид
00
0
1
(),(
0
0
()
yy xx yx
yx
′
−=− −
′
. (4.7)
)
≠
47
Правило Лопиталя
Пусть функции
()
f
x и дифференцируемы в некоторой окрестности ()gx
точки
0
x
, за исключением, быть м
0
x
ожет, самой точки . Если
( ) lim ( ) 0
xx xx
fx gx
→→
00
li
=
=
или
00
lim ( ) lim ( )
xx xx
fx gx
→→
=
=∞m
,
то
00
lim lim
() ()
xx xx
() ()
f
xfx
′
при условии, что предел
gx g x
→→
=
′
, (4.8)
0
()
lim
()
xx
f
x
gx
→
′
′
существует (правило Лопиталя этом точка ). При
0
x
может быть как конечной, так и несобственной точкой равной
+∞
или .
Примеры решения задач
Пример 4.14. Найти уравнение касательной и нормали к кривой
точке .
ение. ак как ,
−∞
2
yx x=+
в
0
1x =
00
()2yyx==() 2 1yx x
′
=
+
и
(1) 3y
′
=
Реш Т , то из (4.6) полу-
чаем уравнение
или
касательной
23( 2)yx−= − 34yx
=
− ,
а из (4.7) – уравнение нормали
1
2(
3
yx−=− −
2)
или
18
2
33
yx
−
=− + .
аименьший угол между кривымиПример 4.15. Найти н () 5 6
f
xx=− и
=
Решение. Найдем точки пересечения графиков данных функций:
0
2
x
.
()gx
22
56 56
x
xxx−= ⇒ − +=.
е сечения
2x
=
и
3x
Отсюда абсциссы точек п ре
1 2
=
. Тогда точки пересе-
чения
оме
имеют координаты
1
(2;4)M
и
2
(3;9)M
. Кр того,
() 5fx
′
=
и
() 2gx x
′
=
,
т.е.
(2) (3)ff
′′
5==
и
g
′
(2) 4=
,
(3) 6g
′
=
. По формуле (1.19) находим угол меж-
ду касательными:
11
54 1 1
tg arctg
154 21 21
ϕϕ
−
==⇒=
+⋅
;
22
65 1 1
tg arctg
156 31 31
ϕϕ
−
==⇒=
+⋅
.
48

ln
lim
x
x
x
→∞
Пример 4.16. Найти .
Решение Имеем неопределенность вида
∞
⎧
⎫
⎨
⎬
∞
⎩⎭
. . Для ее раскрытия восполь-
зуемся правилом Лопиталя (4.8):
()
()
ln
ln 1 1 2
lim lim lim : lim 0
xxx x
x
x
x
x
→∞ →∞ →∞ →∞
∞
⎛⎞⎛⎞
⎧⎫
====
⎨⎬
⎜⎟⎜⎟
∞′
⎩⎭
.
2 xx
x
′
⎝⎠⎝⎠
имер 4.17. Най
Пр ти
0
ee
lim
x
x−
−
.
ln(1 )
x
+
x
→
0
Реш то неоп деленение. Имеет мес ре ность вида
0
⎧
⎫
⎨
⎬
. Используем правило
⎩⎭
Лопиталя:
()
()
000
ee ee
lim li lim 2
1
ln(1 ) 0
)
1
xx xx
xxx
x
x
ee
0
m
xx
ln(1
x
−
−−
→→→
−+
⎧⎫
== = =
⎨⎬
+
′
⎩⎭
+
′
−
+
.
имер 4.18. НайтиПр
2 x
2
e1
lim
x
0
sin 3
x
→
−
.
ение. Раскрываем неопределенность вида
0
0
⎧
⎫
⎨
⎬
⎩⎭
Реш
, используя правило
Лопиталя:
()
()
2
2
2
e
0 2e1
lim l lim
0 3
x
x
x
x
x
2x
2
000
sin 3 6sin cos3
sin 3
xx
e
im
x
xx
x
→→→
′
⎩⎭
′
−
⎧⎫
== =
⎨⎬
.
−−
Опять получили неопределенность вида
0
0
⎧
⎫
⎨
⎬
. Применяем повторно пра-
⎩⎭
вило Л
x→
опиталя. При этом, т.к.
lim 6cos3 6x
0
=
, то получаем
()
()
2
22
2e 1
2e 1 1 1 4e
lim lim lim
x
xx
′
−
−
000
1 4 2
6sin3 cos3 6 6 3cos3 6 3 9
sin3
xxx
xx x
x
→→→
=
==⋅=
′
.
Пример 4.19. Найти
ln
lim
x
x
x
→+∞
.
. Раскрывая неопределенность по правилу Лопиталя, получаем: Решение
49
()
ln
ln 1
lim lim lim 0
xxx
x
x
xx
→+∞ →+∞ →+∞
′
∞
x
⎫⎧
=
===
⎬
′
∞
⎩⎭
.
Пример 4.20. Вычислить
⎨
1
0
lim( )
x
x
x
ex
→
+
.
Решение. Имеем неопределенность вида
{
}
1
∞
. Обозначим искомый пре-
дел че
1
0
lim( )
x
x
x
A
ex
→
=+
рез
A
, т.е. . Прологарифмируем обе части последнего ра-
венст в числи олученный предел:
ва и ы м п
11
00 0
ln( )
ln ln
=+
lim( ) lim ln( ) lim
x
xx
xx
xx x
ex
Aex ex
x
→→ →
⎛⎞⎛⎞
+
=+= =
⎜⎟⎜⎟
⎝⎠⎝⎠
()
00
ln( )
01
li
0
x
→→
⎧⎫
== =
⎨⎬
⎩⎭
m lim 2
x
x
x
x
ex
e
xex
′
+
+
=
′
+
.
Значит
2
A
e= .
Задани для самостоятельного решения
4.21. Составить уравнение касательной и нормали к графику функции
= чке с циссой
я
()x в то абсyf
0
x
.
;
3
0
() , 2fx x x==
2)
0
() cos, /4fx xx
π
=
=
1)
;
)
() , 1
x
fx e x==
;
() 2 5, 0,5fx x x x=−+ =
;
)
3
0
0
4)
2
2
1, 2x+ =
; 6)
2
fx x
0
()fx x=
x
0
() 0,5sin(4 /3), /6
π
π
=
;
=−
5
7)
1
0
() , 1fx x x
−
==−
; 8)
0
() ln,
f
xxxxe
=
=
.
4.22. Написать уравнения касательных к графику функции ()yfx= в
0
x
точке с абсциссой
. Построить кривые и касательные:
1)
0
4
2, 2fx x
x
=+ =; 2)
1
()
2
0
() 1 2, 0fx x x
=
−+ =
;
3)
0fx x x x=++ =
; 4)
2
0
() 1
2
0
() , 1fx x xx
=
−=, −
.
4.23. од каким углом пересеваются кривые;
1)
П
3
12
() , ()fx x x gx
x
=
−=
2
() , () 1
f
xxgx x==−
; 2) ;
3)
1
() , ()
f
xxgxx
−
==
; 4)
2
() , ()
f
xxgxx
=
=
;
2
() , () 1
f
xxgx x==−
; 6
5)
) () sin , () cos
f
xxgx x
=
= .
4.24. айти угол между касательными к графику функции в
точках с абсциссами
Н ()yfx=
1
x
=
−
и
1
x
=
:
50
