Румянцев Н.В., Медведева М.И., Полшков Ю.Н., Пелашенко А.В. Практикум по решению задач курса Высшая математика
Подождите немного. Документ загружается.

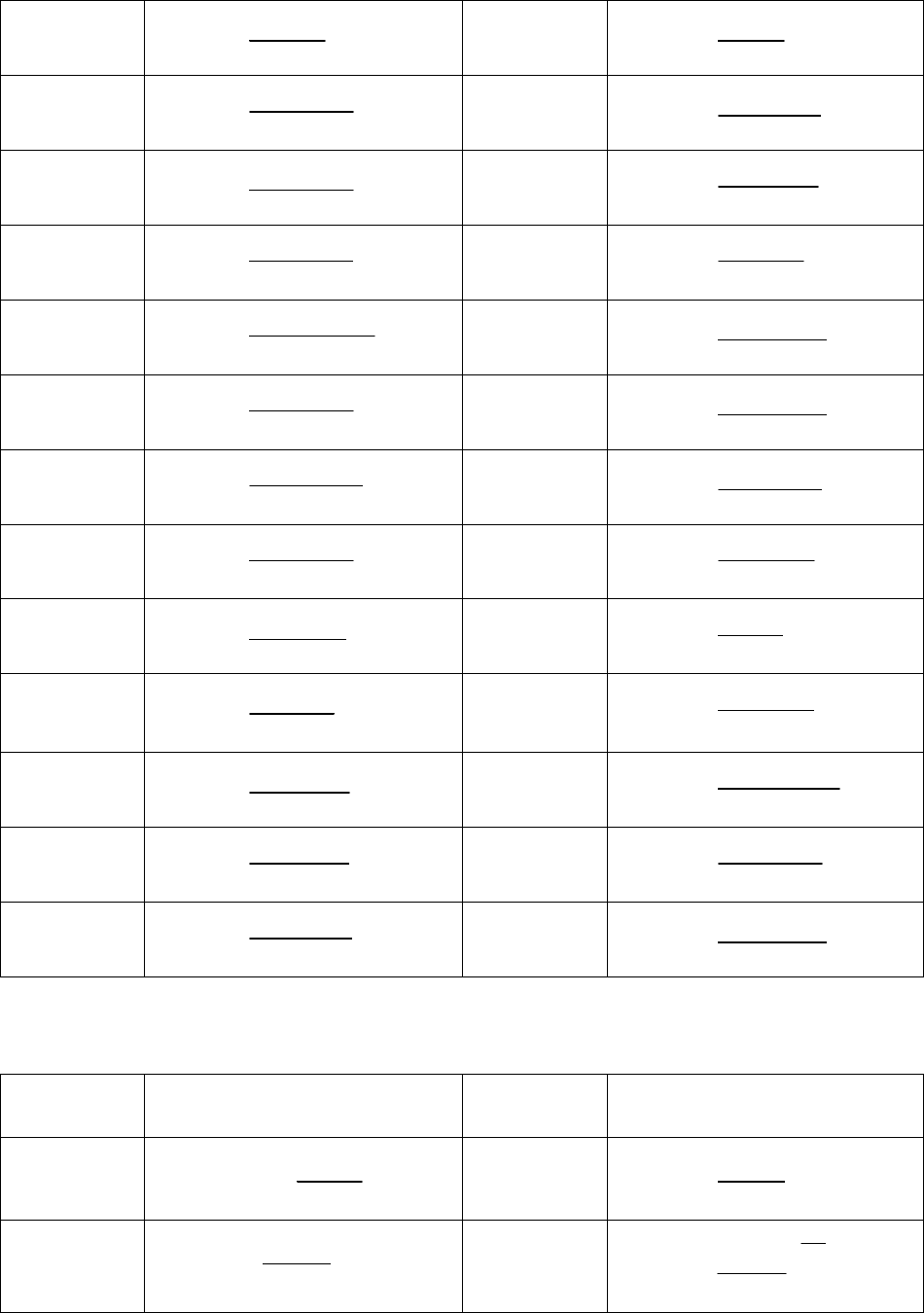
Окончание табл. 8.3
3
2
2
0
2
lim
sin 3
x
x
x
→
18
2
0
5
lim
sin 2
x
x
x
→
4
2
0
1cos4
lim
3
x
x
x
→
−
19
2
0
lim
1cos3
x
x
x
→
−
5
2
0
sin 5
lim
1cos2
x
x
x
→
−
20
2
0
arcsin 2
lim
5
x
x
x
→
6
2
0
1cos6
lim
5
x
x
x
→
−
21
0
10
lim
arctg5
x
x
x
→
7
2
0
arcsin13
lim
sin 3
x
x
x
x
→
22
2
0
arcsin 3
lim
1cos2
x
x
x
→
−
8
2
0
1cos7
lim
7tg2
x
x
x
→
−
23
2
0
arcsin 3
lim
7
x
x
x
→
9
2
0
7arctg5
lim
sin 3
x
x
x
x
→
24
2
0
sin 5
lim
1cos6
x
x
x
→
−
10
0
100
lim
1cos2
x
x
x
→
−
25
2
0
3
lim
arctg 3
x
x
x
→
11
2
0
arcsin
lim
2
x
x
x
→
26
2
0
sin5
lim
2
x
x
x
→
12
2
0
2
lim
arctg3
x
x
x
→
27
2
0
7
lim
arctg5
x
x
x
→
13
2
0
6
lim
arcsin 2
x
x
x
→
28
0
sin3
lim
33cos2
x
x
x
→
−
14
0
sin 4
lim
6arctg6
x
x
x
→
29
2
0
1cos2
lim
arctg 7
x
x
x
→
−
15
2
0
1cos5
lim
sin 2
x
x
x
→
−
30
2
2
0
lim
arcsin 3
x
x
x
→
Задание 8.4. Вычислить предел функции . табл. 8.4):
Таблица 8.4
Номер
варианта
Номер
варианта
(см
1
3
1
lim 1
21
х
x
x
+
→∞
+
⎝⎠
⎛⎞
+
⎜⎟
16
5
83
lim
31
x
x
x
x
+
→∞
+
−
⎝
⎛⎞
⎜⎟
⎠
2
32
93
lim
19
x
x
x
x
−
→∞
−
⎛⎞
⎜⎟
+
⎝⎠
17
1
3
13
lim
73
x
x
x
x
−
→∞
+
⎛⎞
⎜⎟
+
⎝⎠
31
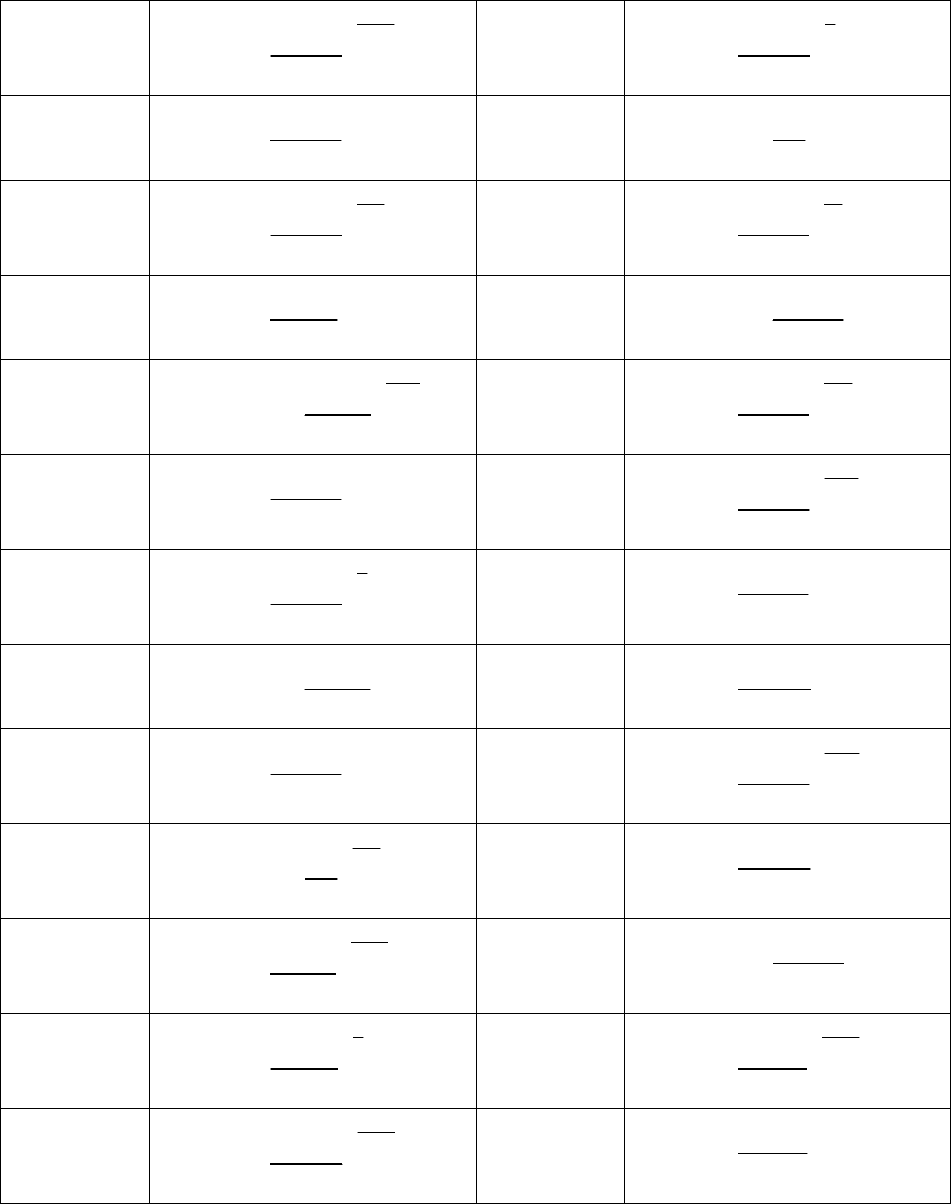
Окончание табл. 8.4
3
25
7
45
lim
51
x
x
x
x
+
→∞
+
⎛⎞
⎜⎟
−
⎝⎠
18
5
3
24
lim
32
x
x
x
x
+
→∞
−
⎛⎞
⎜⎟
+
⎝⎠
4
10
21
lim
23
x
x
x
x
−
→∞
−
⎛⎞
⎜⎟
+
⎝⎠
19
51
3
lim 1
7
х
x
x
−
→∞
⎛⎞
+
⎜⎟
⎝⎠
5
3
2
53
lim
54
x
x
x
x
−
→∞
−
⎛⎞
⎜⎟
+
⎝⎠
20
3
5
2
34
lim
31
x
x
x
x
→∞
+
⎛⎞
⎜⎟
−
⎝⎠
+
6
5
17
lim
71
x
x
x
x
+
→∞
+
⎛⎞
⎜⎟
−
⎝⎠
21
11 5
2
lim 1
34
х
x
x
+
→∞
⎛⎞
−
⎜⎟
−
⎝⎠
7
31
7
5
lim 1
51
х
x
x
−
→∞
⎛⎞
−
⎜⎟
+
⎝⎠
22
5
2
12
lim
32
x
x
x
x
+
→∞
+
⎛⎞
⎜⎟
+
⎝⎠
8
75
34
lim
31
x
x
x
x
+
→∞
−
⎛⎞
⎜⎟
+
⎝⎠
23
51
3
23
lim
31
x
x
x
x
−
→∞
+
⎛⎞
⎜⎟
−
⎝⎠
9
5
3
75
lim
71
x
x
x
x
−
→∞
+
⎛⎞
⎜⎟
−
⎝⎠
24
21
95
lim
53
x
x
x
x
−
→∞
+
⎛⎞
⎜⎟
+
⎝⎠
10
34
9
lim 1
31
х
x
x
+
→∞
⎛⎞
−
⎜⎟
+
⎝⎠
25
23
22
lim
23
x
x
x
x
+
→∞
+
⎛⎞
⎜⎟
−
⎝⎠
11
54
23
lim
21
x
x
x
x
−
→∞
−
⎛⎞
⎜⎟
−
⎝⎠
26
71
3
51
lim
57
x
x
x
x
−
→∞
+
⎛⎞
⎜⎟
−
⎝⎠
12
3
2
8
lim 1
7
х
x
x
+
→∞
⎛⎞
−
⎜⎟
⎝⎠
27
75
24
lim
45
x
x
x
x
+
→∞
+
⎛⎞
⎜⎟
−
⎝⎠
13
25
3
31
lim
31
x
x
x
x
−
→∞
+
⎛⎞
⎜⎟
−
⎝⎠
28
57
4
lim 1
32
х
x
x
+
→∞
⎛⎞
+
⎜⎟
−
⎝⎠
14
3
7
17
lim
71
x
x
x
x
−
→∞
+
⎛⎞
⎜⎟
−
⎝⎠
29
25
7
35
lim
13
x
x
x
x
+
→∞
−
⎛⎞
⎜⎟
+
⎝⎠
15
27
3
61
lim
26
x
x
x
x
−
→∞
−
⎛⎞
⎜⎟
+
⎝⎠
30
8
85
lim
83
x
x
x
x
→∞
−
⎛⎞
⎜⎟
−
⎝⎠
32

Задание 8.5. Исследовать на непрерывность функцию, построить ее гра-
фик (см. табл. 8.5):
Таблица 8.5
Номер
варианта
Номер
варианта
1
2
1, 1,
2,1 3,
1, 3;
x
xx
yx x
+≤
⎧
⎪
=
<≤
⎨
⎪
16
xx
yx x
⎧
−<
⎪
3, 0,
3, 0 2,
>
⎩
2
,2;
xx
=
+≤<
⎨
⎪
≥
⎩
2
2
1, 0,
21,0 1
3, 1;
xx
yx x
x
⎧
−<
⎪
,
=
+≤≤
⎨
⎪
>
⎩
17
3,1 1,
1, ;
x
yxx
x
⎧
−
⎪
2
3, 1,
x
<−
1
=
−− −< ≤
⎨
⎪
>
⎩
3
2
1, 1,
2, 1 0,
3, 0;
x
yx x
xx
⎧
≤−
⎪
=
+−<<
⎨
⎪
≥
⎩
18
2
25, 0,
5, 0 3,
1, 3;
xx
yx x
x
+≤
⎧
⎪
=
+<≤
⎨
⎪
>
⎩
4
32, 2,
1, 2 1,
2, 1;
xx
yx x
xx
−<−
⎧
⎪
=
+−<<
⎨
⎪
>
⎩
19
32, 1
,1 3,
23, 3
xx
yx x
xx
−<
⎧
⎪
=<<
⎨
⎪
−>
⎩
,
;
5
2, 1,
21,1 1
1, 1;
xx
yx x
x
−<−
⎧
⎪
,
=
−−<<
⎨
⎪
>
⎩
20
2
32, 0,
3, 0 1,
0, 1;
xx
yx x
x
−≤
⎧
⎪
=
+<≤
⎨
⎪
>
⎩
6
2
,0,
3,0 2
23, 2;
xx
yx x
xx
<
⎧
⎪
,
=
≤<
⎨
⎪
−>
⎩
21
2
1, 1,
1, 1 2,
21, 2;
x
yx x
xx
<−
⎧
⎪
=
+−≤<
⎨
⎪
+>
⎩
7
2
3, 1,
1, 1 1,
1, 1;
x
yx x
xx
<−
⎧
⎪
=
+−≤<
⎨
⎪
+≥
⎩
22
23, 1,
2, 1 2,
1, 2;
xx
yx x
x
−<
⎧
⎪
=
−<<
⎨
⎪
≥
⎩
8
1, 0,
1, 0 2,
1, 2;
xx
yx
xx
+≤
⎧
⎪
=
<<
⎨
⎪
−>
⎩
23
2
2
,1,
23,1 2,
4, 2;
xx
yx x
xx
⎧
−<−
⎪
=
−−≤≤
⎨
⎪
>
⎩
Окончание табл. 8.5
33
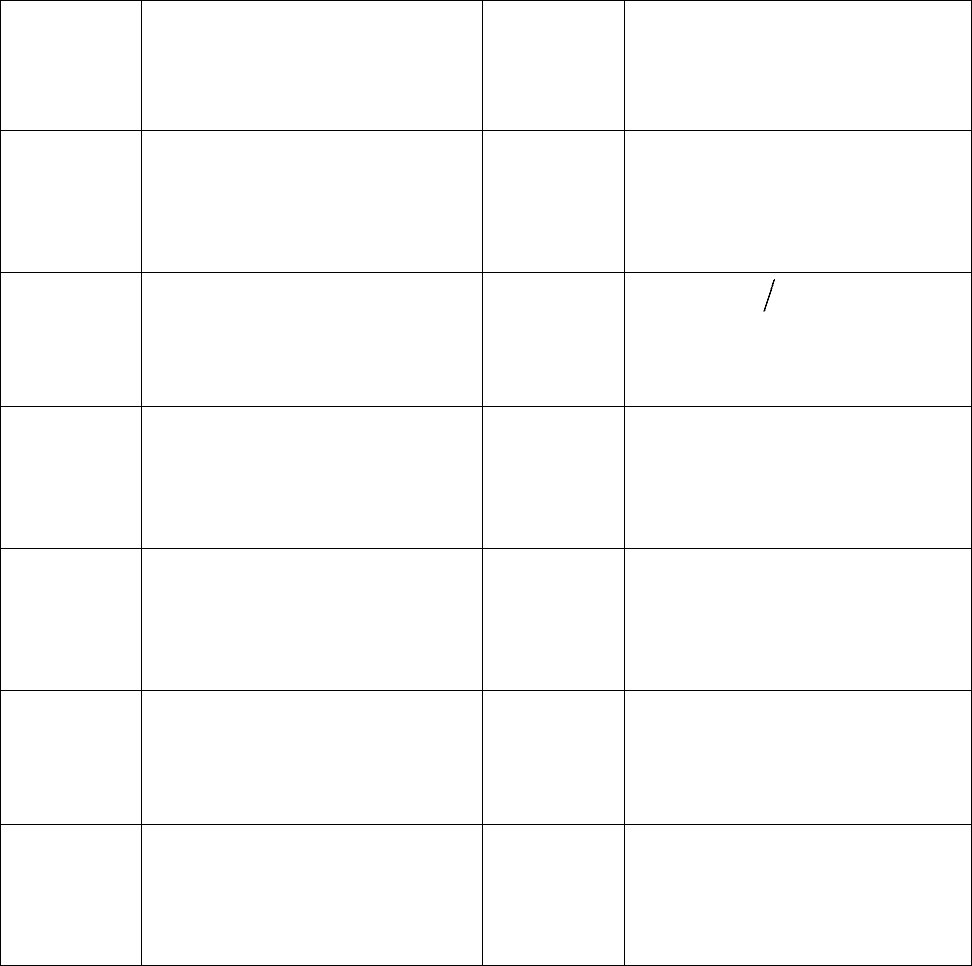
,
,
3, 1;
xx
yx x
х x
−≤−
⎧
⎪
9
2, 1,
2,1 0
32, 0;
x
yxx
xx
<−
⎧
⎪
=−−≤<
⎨
⎪
+≥
⎩
24
3, 2,
24,2 1
=
+−<≤
⎨
⎪
−>
⎩
10
,
25
2
31, 0,
1, 0 1,
1, 1;
xx
yx x
x
−<
⎧
⎪
=
−≤≤
⎨
⎪
>
⎩
2
1, 2,
21,2 1
3, 1;
xx
yx x
x
⎧
−≤−
⎪
=+−<≤
⎨
⎪
>
⎩
11
;
26
0, 0,
,0 3,
23, 3
x
yx x
xx
<
⎧
⎪
=<<
⎨
⎪
−>
⎩
2
2, 3,
2,3 1,
xx
yxx
⎧
<−
⎪
=
−−≤<
⎨
1, 1;x
⎪
>
⎩
12
7, 2;
xx
yx x
x
⎧
+≤−
⎪
=+−<≤
⎨
⎪
>
⎩
2
5, 1,
31,1 2,
27
52, 2,
3, 2 1,
22, 1;
xx
yx x
xx
−≤−
⎧
⎪
=
+−<≤
⎨
⎪
+>
⎩
13
2
1, 1,
3, 1 2,
41, 2;
xx
yx x
xx
−≤
⎧
⎪
=+<≤
⎨
⎪
−>
⎩
1, 2;
xx
yx x
x
⎧
+<−
⎪
28
2
1, 1,
3, 1 2,
=
+−≤<
⎨
⎪
>
⎩
14
2, 3,
3,3 0
3, 0;
xx
yxx
x
<−
⎧
⎪
=−−≤
,
⎨
⎪
>
⎩
;
≤
29
3, 3,
1, 3 4,
27, 4
xx
yx
х x
−
≤
⎧
⎪
=
<≤
⎨
⎪
−>
⎩
15
2
1, 1,
1, 1 0,
1, 0;
xx
yx x
x
⎧
−≤−
⎪
=+−<≤
⎨
⎪
>
⎩
,
30
0, 2,
24,2 3
1, 3.
x
yx x
x
≤
⎧
⎪
=
−<≤
⎨
⎪
>
⎩
РАЗДЕЛ 4
34
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
ТЕМА 1
ПРОИЗВОДНАЯ ФУНКЦИИ
Понятие производной
Пусть функция определена и непрерывна на некотором интерва-
. Производной функции
()yfx=
(
)
f
x
по незави
(, )ab ле
симой переменной
x
называет-
ся предел отношения приращения функции y
∆
к приращению аргумента
x
∆
,
когда приращен
ие аргумента стремится к нулю, т.е.
00
()()
lim lim ( )
xx
fx x fx y
f
x
xx
∆→
+∆ − ∆
∆→
′
==
∆∆
.
Если этот предел конечен, то функция ()yfx
=
называется дифференци-
руемой в точке
x
. Если
()fx
′
=
∞
, то вор функция имеет в
точке
го ят, что ()yfx=
x
бесконечную производную.
Производная обозначается
(
)
yyx
′
′
=
,
(
)
f
x
′
или
dy
dx
.
Операция нахождения производной называется дифференцированием.
Число
0
()()
() lim
x
f
xxfx
fx
x
+
∆→+
+
∆−
′
=
∆
называется правосторонней производной в точке
x
. Число
0
()()
) lim
x
(
f
xxfx
fx
x
−
∆→−
+
∆−
′
=
∆
.
назыв одной в точке
x
ается левосторонней произв .
Производная
()
f
x
′
функци x ()yfи
=
существует гда и только тогда,
когда
то
() ()
f
xfx
−+
′′
Дифференцирование явно заданных функций
Основные правила дифференцирования
)
=
.
1)
0C
′
=
, где
C
– постоянная величина;
(
)
(
)
(() ())ux vx u x v x
′′ ′
±=±
2
;
3)
′
′′
⋅=⋅+⋅;
( ) () () () ()
() ()ux vx u x vx v x u x
35
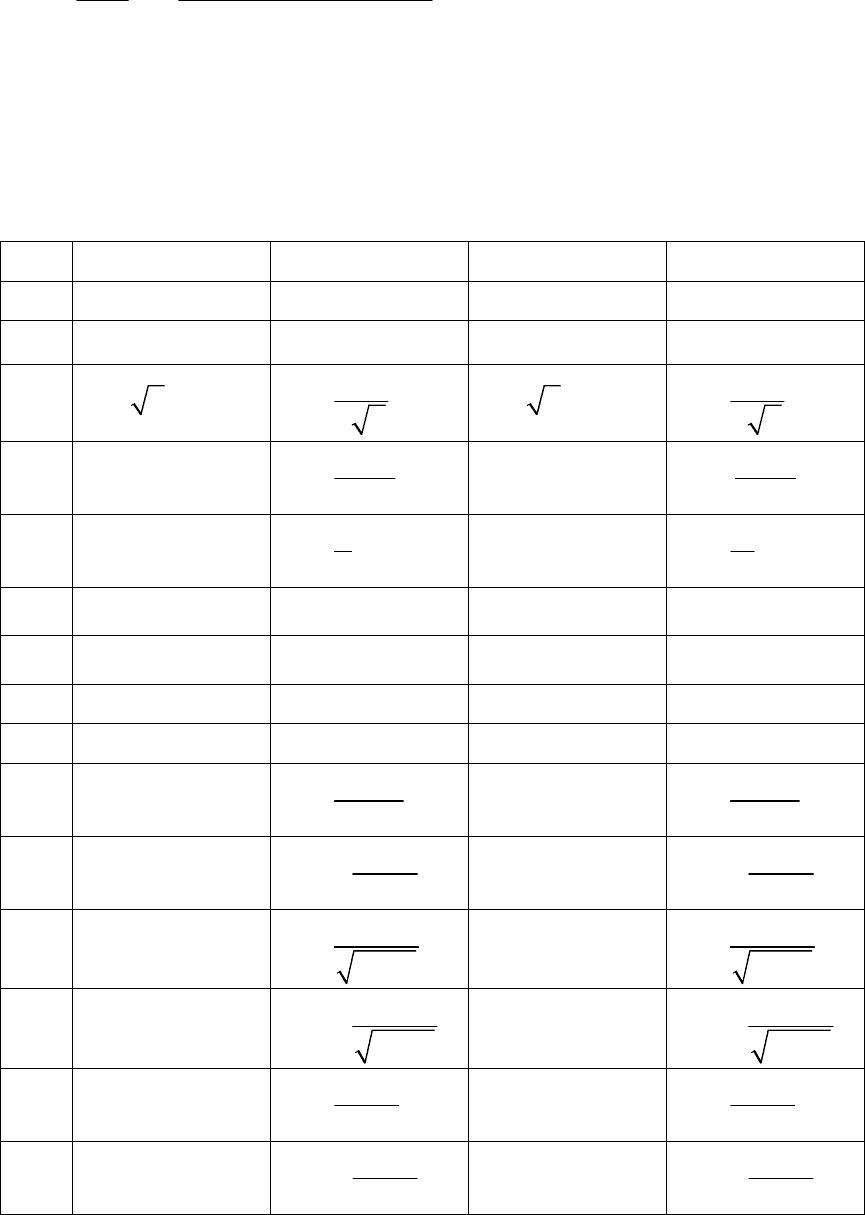
4)
()()
() ()сu хсu х= ,
C
– постоянная вели ин
′′
ч а;
()() () ()
()
2
()
xv x
vx
vx
=
⎜⎟
⎝⎠
()
u x uxv
ux
′
′′
−
⎛⎞
, ( ) 0vx
≠
5)
;
6) если функция ()ux
ϕ
= дифференцируема в точке
0
x
, а функция
дифференц()yfu= ируема в точке
00
()ux
ϕ
=
, то сложная ф (())yf x
ϕ
=ункция
дифференцируема в точке
0
x
и
() ()()ux
′′′
00xu 0x
yx yu
=
.
Таблица производных основных элементарных функций
yC=
0y
′
=
1.
2.
1y
yx=
′
=
3.
n
yx=
1n
ynx
−
′
=
1n
ynuu
−
′
′
=
n
yu
=
yx=
1
2
y
x
′
=
yu=
2
u
y
u
′
′
=
4.
1
ln
y
5.
log
а
y
х
=
x
a
log
a
yu
′
=
=
1
ln
yu
ua
′
′
=
6.
lny
х
=
u
y
u
′
′
=
1
y
x
lnyu
=
′
=
7.
x
ya=
ln
x
ya a
′
=⋅
u
ya
=
ln
u
ya au
′
′
=
⋅⋅
8.
x
ye=
x
ye
′
=
u
ye
=
u
yeu
′
′
=
⋅
9.
sinyx=
cosyx
′
=
sinyu
=
cosyuu
′
′
=
⋅
10.
cosyx=
sinyx
′
=−
cosyu
=
sinyuu
′
′
=
−⋅
11.
tgyx=
2
1
cos
y
x
′
=
tgyu
=
2
cos
u
y
u
′
′
=
12.
ctgyx=
2
1
sin
y
x
′
=−
ctgyu
=
2
sin
u
y
u
′
′
=−
13.
arcsinyx=
2
1
1
y
x
′
=
−
arcsinyu
=
2
1
u
y
u
′
′
=
−
14.
arccosyx=
2
1
1
y
x
′
=−
−
arccosyu
=
2
1
u
y
u
′
′
=−
−
15.
arctgyx=
2
1
1
y
x
′
=
+
arctgyu
=
2
1
u
y
u
′
′
=
+
16.
arcctgyx=
2
1
1
y
x
′
=−
+
arcctgyu
=
2
1
u
y
u
′
′
=−
+
Производные высших порядков.
36
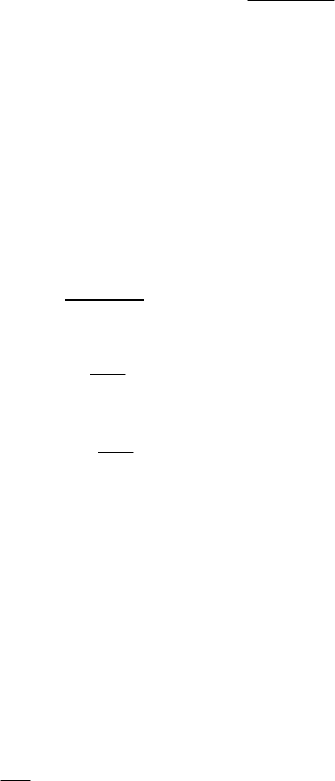
Формула Лейбница
Если производная ) – го порядка функции (1n − ()yfx
=
уже определена,
то производная
– го порядка определ етс равенством
n
() ( 1)
() ()
nn
yx y x
−
′
⎡⎤
=
⎣⎦
я я . В
частн
)yx y
[]
() ()yx yx
′
′′ ′
= ,
[]
() (x
ости
′
′′′ ′′
= и т .
Если и –
раз дифференцируемые функции, то
.д
()ux ()vx
n
[]
[
]
[
]
() () ()
12 1 2
() () () ()
nn
cu x c v x c u x c v x+= +
n
,
где – произвольные постоянные.
Для произведени
12
,cc
я () ()ux vx
⋅
справедлива формула Лейбница
[]
()
) ( 1) ( 2 ()
(1)
12
n
n n n
nn
uv u v nu v u uv
−−
( )
...
n
v
−
′′
⋅= + + =
′
++
⋅
)
n
knk k
n
−
0
k
Cu v
=
=
∑
. (4.1)
дую и
()(
Верны сле щ е формулы:
()
() ( 1)...( 1)
mn mn
x
mm m n x
−
=− −+
1)
;
2)
, в частности
()
() ln,( 0)
xn x n
aaaa=>
()
()
x
nx
ee
=
;
3)
() 1
(1)!
nn
n
(ln ) ( 1)x
n
x
−
−
; =−
()
(sin ) sin
2
n
n
xx
π
⎛⎞
=+
⎜⎟
⎝⎠
4)
; (4.2)
5)
()
) cos
n
(cos
2
n
xx
π
⎛⎞
⎜⎟
⎝⎠
.
обратных функций и
функций, заданн параметрически
сть функция
=+
(4.3)
Дифференцирование
ых неявно или
Пу (
ax
()yfx=
b
<
<
функцию
) дифференцируема и имеет однознач-
ную непрерывную обратную ()
x
gy
=
и
0
x
y
′
≠
, то обратная функция
также ф еренцируема и ди ф
1
y
x
x
y
′
=
′
.
В частно авенство
сти для производной второго порядка имеет место р
37
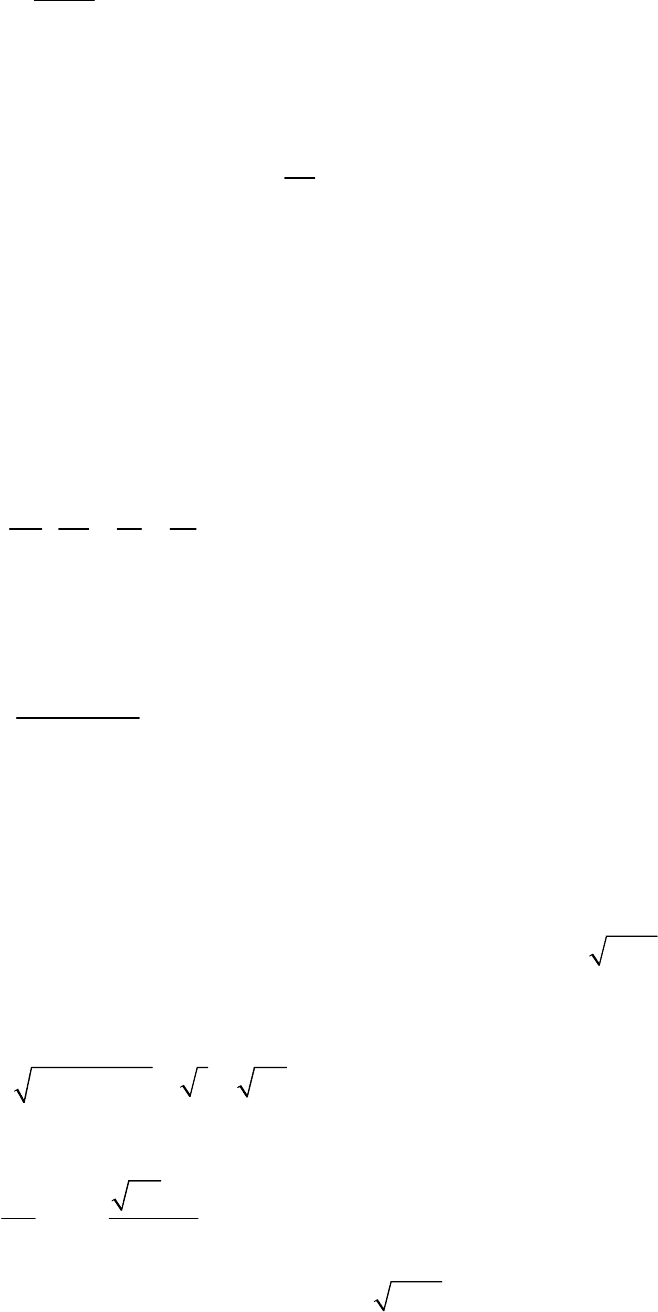
2
()
x
x
yy
x
y
x
y
′
′
′′
=−
′
.
(, ) 0Fxy
=
Пусть дифференцируемая функция задана неявно уравнением .
Для вычислен производной надо продифференцировать уравнение (, ) 0Fxy
=
ия
по переменной
x
и полученное уравнение (, ) 0
d
Fxy
dx
=
решить относительно
x
y
′
.
Пусть однозначная непрерывная функция от переменной
x
задана систе-
мой уравнений
(),
,
(),
yut
t
xvt
α
β
=
⎧
<<
⎨
=
⎩
где ()ut и ()vt – дифференцируемые ф
) 0t
ункции и
v
(
′
x
y
′
≠
. Тогда производная
также существует и определяется равенством
x
′
:
tt
tt
Производные высших порядков вычисля
ти, производная второго порядка вычисляется
du dv u y
y
dt dt v x
′′
===
′′
. (4.4)
ются последовательно. В частно-
по формуле:
с
2
()
ttt ttt
xx
t
x
yxy
y
x
′′′ ′′′
−
′′
=
′
.
Пример 4.1. Найти приращение
Примеры решения задач
y
∆
функции
2
yx
=
при
0
x
=
и
0,001
x
∆=
.
Решение.
yx∆= +∆
ример 4.2. Исследовать дифференцируемость функции
22
) 0,000001x x− =
.
(
П
3
1yx=−
в точ-
ке
x
= . 1
Решение. При
1
x
=
приращение функции имеет вид:
3
3
3
1 ) 1 1 1yx x∆= +∆ −− = ∆−. (
Тогда
3
00
1
lim lim
xx
yx
xx
∆→ ∆→
∆∆−
==
∆∆
∞
.
Следовательно, в точке
1
x
=
функция
3
1yx
=
−
не имеет конечной про-
изводной.
Пример 4.3. Исследовать дифференцируемость функции . arccos(sin )yx=
38
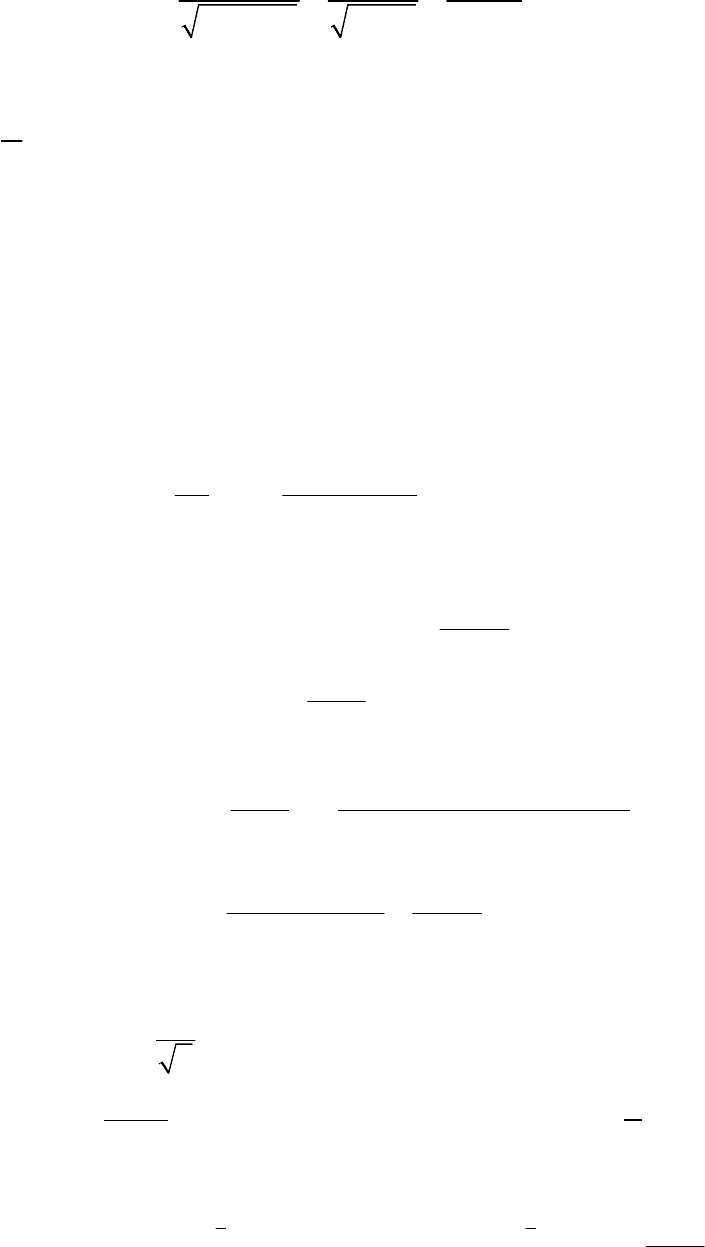
Решение.
22
s |
1 cos
cos cos cos
|co
sin
x
xx
y
x
xx
==
−
.
едовательно,
1y
′
=
, если
cos 0
′
=
x
>
;
1y
′
=
−
, еслСл и
cos 0
x
<
. В точках
2
x
k
π
π
=+
, ( 0, ,.k =±1, 2 ..)± , где
cos 0
x
=
, функция непрерывна не диффе-
ренци
ример 4.4. Пользуясь определением производной, найти производную
функции
, но
руема.
П
2
()
f
xx=
в точке
0
3x
=
.
е. Найдем приращение функцииРешени
2
()
f
xx
=
в точке :
2
∆
.
0
3x =
22
(3 ) (3) (3 ) 3 6 ( )yf x f x x x∆= +∆ − = +∆ − =∆+
Тогда
()
2
00 0
6
lim lim
yx∆∆−()
lim 6 6
xx x
x
x
xx
∆→ ∆→ ∆→
∆
==∆=
∆∆
.
аким образом, .
Пример 4.5. Доказать, что
+
(3) 6y
′
=
Т
2
1
(tg )
cos
x
x
′
= .
sin
tg
cos
x
x
x
= ,
(sin ) cos
x
x
′
=
,
(cos ) sin
x
x
′
=
Решение. Так как
, то
2
sin (sin ) cos sin (cos )
(tg )
cos cos
x
xx xx
′
x
xx
′
′
−
⎛⎞
′
== =
⎜⎟
⎝⎠
22
cos sin 1xx
22
cos cos
x
x
Пример 4.6. Найти производные следующих функций:
+
==.
2
5
2
sin logyx x x
x
=− + +
; 2)
5cos(2 3)
x
yx
=
+
;
1)
3
1
x
e
3)
y
x
=
+
; 4)
2
1
sin tgy
x
⎛⎞
=
⎜⎟
⎝⎠
.
ешение.
1)
Р
13
2
22
5
1
2sinlog 2 cos
ln 5
yx x x x xx x
x
−−
′
⎛⎞
′
=− + + =++ +
⎜⎟
⎝⎠
;
()()
()
5 cos(2 3) 5 cos(2 3) 5 cos(2 3)
xxx
yx x x
′′
′
′
=⋅ += ⋅ ++⋅ +=
2)
39

ln 5 cos(2 3) 5 sin(2 3) 2 3
xx
xxx
()
5
′
=⋅ +−⋅ ++=
.
5ln5cos(2 3) 52sin(2 3)
xx
xx=⋅ +−⋅ +
3332
332 3
()(1 ) (1 ) (1 )3
1(1)(1)
xx x x
eexexexxe
2
x
xx x
′
′′
⎞
⋅+ − ⋅+ + − ⋅
= =
⎟
++ +
⎝⎠
y
⎛
′
==
⎜
3)
32
32
(31)
x
ex x−+
=
.
(1 )x+
4)
2
1111
sin tg 2sin tg cos tgy
′
⎡⎤
22
1
cos (1/ )xxxxx
⎛⎞ ⎛⎞ ⎛⎞
−=
⎜⎟
⎝⎠ ⎝⎠⎝⎠ ⎝⎠
⎣⎦
⎛⎞
′
==⋅⋅
⎜⎟ ⎜⎟⎜⎟
⎢⎥
(
)
22
sin 2tg(1/ )
cos (1/ )
x
x
x
=−
.
для
2
x
Пример 4.7. Найти производную второго порядка функции ye= .
Решение. Находим производную первого порядка:
−
2
()
22
2
() 2
x
xx
ye e x xe
−−
′
′′
==⋅−=−
−
.
Теперь находим производную второго порядка:
)
2222
2 2(2)
xxxx
xexe exxe
−−−−
⎛⎞
′
⋅ + ⋅ =− + ⋅− =
⎜⎟
⎝⎠
()
2
2
x
yxe
−
′′
′′
=− =−
()(
(
)
(
)
22
22
212 2 2
xx
exex
−−
=− − = −1
.
Пример 4.8. Применяя формулу Лейбница, найти для функции
yx=
(20)
y
2
cos x
.
Решение. Так как
(
)
()
2
0
n
x =
при
3n
, то из (4.1) имеем
≥
(
)
() ()
(20)
(20) (19)
(20) 2 2 2
cos cos 20 cos ( )yxx xx xx
′
==+
+
()
(18)
2
20 19
cos ( )
2
x
x
⋅
′
′
+
,
Отсю а и равенств (4.2), (4.3)
д
40
