Румянцев Н.В., Медведева М.И., Полшков Ю.Н., Пелашенко А.В. Практикум по решению задач курса Высшая математика
Подождите немного. Документ загружается.

lim 1
n
n
n
→∞
= и lim 1 ( 0)
n
n
aa
→∞
=
> .
Тогда
lim3 lim3lim 111
nnn
nnn
nn
→∞ →∞ →∞
=⋅=⋅=.
Пример 3.11. Вычислить
(
)
2
lim 1
n
nn
→∞
+
−
.
Решение. Умножим и разделим выражение
(
)
2
1nn
+
−
на сопряженное
ему выражение
(
)
2
1n++n
. Тогда получаем
(
)
(
)
(
)
22
22
2
22
11
1
lim 1 lim lim
11
nn n
nnnn
nn
nn
nn nn
→∞ →∞ →∞
+− ++
+−
+− = = =
++ ++
2
1
lim 0
1
n
nn
→∞
=
=
++
.
Задания для самостоятельного решения
3.14. Найти первые пять членов последовательность
{
}
n
х
, если
1)
; 2)
sin
3
1
n
х n=−
n
х
n
π
=
; 3)
2
n
х
nn=−
;
4)
1
n
х
n
−
=
; 5)
2
1
1
n
х
n
⎛
=+
⎜
⎝⎠
⎞
⎟
; 6)
sin( / 2)
n
n
х
n
π
= .
3.15. Зная первые члены последовательности, написать одно из возмож-
ных выражений для ее общего члена:
1)
2 5 10 17 26
;; ; ; ;...
3 8 13 18 23
; 2)
1111
1; ;2; ;3; ;4; ;...
2345
;
3)
4 9 16 25 36
1; ; ; ; ; ;...
2 6 24 120 720
; 4)
4141
1;;;;;...
3253
;
5)
2 5 10 17 26 37
;; ; ; ; ;...
12 3 4 5 6
; 6)
1111
1; ; 3; ; 5; ; 7; ; ..
2468
;
7)
11 11 1
1; ; ; ; ; ; .. .
23 45 6
−−−
; 8) 3; 3; 3; 3; 3; 3;...
−
−−;
9) 1 ; 10) 1 . ; 0; 1; 1; 0; 1; 1; 0; 1; .. .−−− ; 7; 31; 127; 511;...
3.16. Найти первые пять членов последовательности
{
}
n
х
, заданной ре-
куррентным соотношением:
1)
; 2)
1
32,
nn
xxx
+
=− =
1
1
1
123
,1,
n
n
n
x
xxx
x
−
+
2
=
==
;
11
3) ; 4)
112 1
... , 2
nn
xxx xx
+
=+++ =
11
11
,2
2
nn
n
xx x
x
+
⎛⎞
=
+=
⎜⎟
⎝⎠
.
3.17. Доказать, что последовательность ,… сходится к нулю,
если
23
, , ,...,
n
qq q q
1q <
.
3.18. Доказать, что последовательность
(1)
n
−
не имеет предела.
3.19. Доказать, что последовательность
5
n
1
x
n
=
−
не является сходящейся.
3.20. Пользуясь определением предела доказать, что:
1)
21
lim
31
n
n
n
→∞
−
=
+
2
3
; 2)
2
2
51
lim
24
n
n
n
→∞
− 5
2
=
−
; 3)
2
3
lim 0
2
n
n
n
→∞
=
−
;
4)
11
lim
21
n
n
n
→∞
+
=
− 2
; 5)
2
2
5
lim 1
2
n
n
nn
→∞
+
=
−
; 6)
2
2
41
lim
31
n
n
n
→∞
−
=
− 3
;
7)
21
lim 1
2
n
n
n
→∞
+
=
; 8)
1
lim 1
n
n
n
→∞
−
=
; 9)
1(1)
lim 0
n
n
n
→∞
+−
= .
3.21. Составить последовательности:
1)
возрастающую и сходящуюся к нулю;
2)
убывающую и сходящуюся к двум;
3)
убывающую и расходящуюся;
4)
возрастающую и расходящуюся.
3.22. Найти пределы:
1)
31
lim
52
n
n
n
→∞
+
−
; 2)
2
34
lim
51
n
n
nn
→∞
+
−
+
;
3)
2
2
4
lim
25
n
nn
nn
→∞
−+
+−3
; 4)
2
2
47
lim
36
n
n
nn
→∞
−
+
−
;
5)
215
lim
11
n
nn
nn
→∞
+−
⎛
⋅
⎜
−+
⎝⎠
⎞
⎟
; 6)
41
lim
0, 2 3
n
n
n
→∞
−
+
;
7)
1
(1)
lim
(1)
n
n
n
n
n
+
→∞
+−
−−
; 8) lim 5
n
n
n
→∞
;
9)
lim 7 3
n
n
n
→∞
− ; 10)
(
)
2
lim
n
nnn
→∞
−
−
;
11)
2
lim
2
n
nn
nn
→∞
+−
++
; 12)
(
)
lim 2 1 2
n
nn
→∞
+− ;
13)
5
31
lim
65
n
n
n
→∞
+
⎛
⎜
−
⎝⎠
⎞
⎟
; 14)
8
lim
n
n
n
→∞
;
15)
(
)
lim 2 5 1
n
nn
→∞
+− − ; 16)
22
3
12...
lim
342
n
n
nn
→∞
2
+
++
+−
;
17)
2
1 2 ...
lim
n
n
n
→∞
++ +
; 18)
3
32
245
lim
51
n
nn
nn
→∞
⎛⎞
+
−
⎜⎟
−
+
⎝⎠
;
12
19)
(
)
22
lim 1 1
n
nn nn
→∞
+
+− −+
; 20)
(1)( 2)
lim
( 3)( 4)( 5)
n
nn n
nnn
→∞
++
+
++
;
21)
( 1)( 2)(3 )
lim
(1)(2)(3
n
nn n
nn n
→∞
−−−
+++)
; 22)
2
lim
12
n
n
nn
→∞
+
−+ +
;
23)
(
)
22
lim 2 1 2 3 1
n
nn n n
→∞
+−− − −
; 24)
(
)
23
3
lim
n
nnn
→∞
−+
;
25)
(
)
2
33
lim ( 1) ( 1)
n
nn
→∞
+− −
2
; 26) lim
n
nnn n
→∞
⎛⎞
++ −
⎜⎟
⎝⎠
;
27)
22
1234...2
lim
14 1
n
n
nn
→∞
−+−+ −
+
+−
; 28)
2
3
4
1
lim
1
n
n
nn
→∞
−+
+−
n
;
29)
123...
lim
22
n
nn
n
→∞
+++ +
⎛⎞
−
⎜⎟
+
⎝⎠
; 30)
!
lim
(1)!
n
n
nn
→∞
!
+
−
;
31)
(2)!(1)
lim
(3)!
n
nn
n
→∞
+++
+
!
; 32)
(2)!(1)
lim
( 2)! ( 1)!
n
nn
nn
→∞
!
+
++
+
−+
;
33)
11 1
1...
24
2
lim
11 1
1 ...
39
3
n
n
n
→∞
⎛⎞
++++
⎜⎟
⎜⎟
++++
⎝⎠
; 34)
3
lim
23
n
n
n→∞
+
;
35)
2
21
5
lim
15
n
n
n
+
→∞
+
; 36)
22
lim
22
nn
nn
n
−
−
→∞
−
+
.
ТЕМА 3
ПРЕДЕЛ ФУНКЦИИ
Понятие предела функции. Односторонние пределы
Число
A
называется пределом функции ()yfx
=
при
0
x
x→
, если для
любого
0>
ε
существует () 0
δ
δε
=>, зависящее от
ε
, такое, что для всех
x
,
удовлетворяющих неравенству
0
xx
δ
−
<
справедливо неравенство
()fx A
ε
−<
. Обозначают:
0
lim ( )
xx
f
xA
→
=
,
0
()
xx
f
x
→
→ A
или ()
f
x→ A при
0
x
x→
.
Число
A
называется пределом справа функции ()yfx
=
при
0
x
x→
, если
для любого
0>
ε
существует такое () 0
δ
δε
=
> , что для всех
x
, удовлетво-
ряющих неравенству
0
0 xx
δ
<− <
справедливо неравенство
()fx A
ε
−<
. Обо-
значают:
0
0
lim ( )
xx
f
xA
→+
=
.
Число
A
называется пределом слева функции ()yfx
=
при
0
x
x→
, если
для любого
0>
ε
существует такое () 0
δ
δε
=
> , что для всех
x
, удовлетво-
ряющих неравенству
0
0xx
δ
−<− <
справедливо неравенство
()fx A
ε
−
<
.
Обозначают:
0
0
lim ( )
xx
f
xA
→−
=
.
13

Если , то пишут просто
0
0x =
0
x
→+
или
0
x
→−
и соответственно
(0)
f
+ или (0)
f
− .
Техника вычисления пределов
1) Если существует
0
lim ( )
xx
f
xA
→
=
и
0
lim ( )
xx
gx B
→
=
, то существуют пределы:
а)
000
lim( () ()) lim () lim ()
xx xx xx
f
xgx fx gxA
→→→
±= ± =±B
;
б)
000
lim( () ()) lim ()lim ()
xx xx xx
f
xgx fx gx AB
→→→
⋅= ⋅ =⋅
;
в)
, где
00
lim ( ) lim ( )
xx xx
cf x c f x cA
→→
==
cconst
=
;
г)
(
)
0
00
0
lim ( )
()
lim , lim ( ) 0
() lim ()
xx
xx xx
xx
fx
fx A
fx
gx gx B
→
→→
→
== ≠
.
2) Для всех основных элементарных функций в любой точке их области
определения справедливо равенство
00
0
lim ( ) (lim ) ( )
xx xx
f
xf xfx
→→
=
=
.
3) Частое применение находят следующие пределы:
0
sin
lim 1
x
x
x
→
= – первый замечательный предел;
1
0
1
lim(1 ) lim 1 2,71828...
x
x
xx
xe
x
→→∞
⎛⎞
+= + ==
⎜⎟
⎝⎠
– второй замечательный предел;
0
log (1 )
lim log , ( 0, 1)
a
a
x
x
ea a
x
→
+
=>≠;
0
ln(1 )
lim 1
x
x
x
→
+
= ; (3.1)
0
1
lim ln , ( 0)
x
x
a
aa
x
→
−
=>
. (3.2)
Раскрытие неопределенностей
Если функция
()
f
x определена в точке
0
x
, то вычисление предела вида
xx
0
lim ( )
f
x
сводится к н редственной подстановке значения
0
→
епос
x
вместо
x
и ис-
нию свойств пределов. На практике при вычислени предело фор-
мальная подстановка вместо переменной
пользова и в
x
ее предельного значения приводит
к неопределенностям вида
{}{}
{} {} { }
00
0
, , , 0 , 1 , 0 , .
∞
∞
⎧⎫⎧ ⎫
0
∞
−∞ ⋅∞ ∞
⎨⎬⎨ ⎬
∞
⎩⎭⎩ ⎭
14

1. Для раскрытия неопределенности вида
⎭
⎬
⎫
⎩
⎨
⎧
∞
∞
числитель и знаменатель
(если они являются многочленами относительно независимой переменной
x
)
делят на переменную
x
в старшей степени.
2.
При раскрытии неопределенности вида
⎭
⎬
⎫
⎩
⎨
⎧
0
0
можно попытаться чис-
литель и знаменатель разложить на множители и дробь сократить. Если под
знаком предела стоит тригонометрическая функция, то можно применить пер-
вый замечательный предел.
3.
Неопределенности вида
{
}
∞
−∞
и
{
}
0
⋅
∞
с помощью элементарных
преобразований функции, стоящей под знаком предела, приводят к неопреде-
ленностям вида
⎭
⎬
⎫
⎩
⎨
⎧
∞
∞
или
⎭
⎬
⎫
⎩
⎨
⎧
0
0
.
4.
В случае неопределенности вида
{
}
1
∞
используют второй замечатель-
ный предел.
Эквивалентные бесконечно малые
Функция ()
x
α
называется бесконечно малой при
0
x
x→
, если
0
lim ( ) 0
xx
x
α
→
=
.
Если ()
x
α
и ()
x
β
бесконечно малые при
0
x
x→
и
0
()
lim 1
()
xx
x
x
α
β
→
=
, то ()
x
α
и
()
x
β
называют эквивалентными бесконечно малыми. Обозначают () ()
x
x
α
β
∼ .
Таблица эквивалентных бесконечно малых функций
(()
x
α
– бесконечно малая при
0
x
→
)
1.
sin ( ) ( )
x
x
α
α
∼ ;
6.
ln(1+ ( )) ( )
x
x
α
α
∼ ;
2.
tg ( ) ( )
x
x
α
α
∼ ;
7.
()
1()ln
x
ax
α
α
− ∼ a
;
3.
2
()
1cos()
2
x
x
α
α
− ∼
;
8.
()
1(
x
ex
α
α
− ∼ )
;
4.
arcsin () ()
x
x
α
α
∼ ;
9.
(1+ ( )) 1 ( )
n
x
nx
αα
− ∼
;
5.
arctg ( ) ( )
x
x
α
α
∼ ;
10.
()
1+ ( ) 1
n
x
x
n
α
α
− ∼
Примеры решения задач
Пример 3.12. Исходя из определения предела, доказать, что
2
lim(3 4) 2
x
x
→
−
=
.
Решение. Пусть
ε
– произвольное положительное число. Необходимо до-
казать, что существует такое
0>
δ
, что при всех значениях
x
, удовлетворяю-
15
щих условию
2x −<
δ
справедливо неравенство
(3 4) 2x
ε
−
−<
. Из последне-
го неравенства получаем:
36x
ε
−<
или
32x
ε
−
<
. Тогда, как только
2/3x
ε
δ
−< =
, выполняется требуемое равенство
(3 4) 2x
ε
−
−<
. Следова-
тельно,
.
2
lim(3 4) 2
x
x
→
−=
Пример 3.13. Вычислить
2
2
3ln(
lim
6
x
xx x
x
→
1)
−
−
+
.
Решение. Так как пределы числителя и знаменателя существуют и предел
знаменателя не равен нулю, то
2
2
3ln(1)640
lim
626
x
xx x
x
→
−−−⋅
==
++
3
4
.
Пример 3.14. Вычислить
3
3
24
lim
31
x
xx
x
→∞
+
−
+
.
Решение. Здесь имеем неопределенность вида
⎭
⎬
⎫
⎩
⎨
⎧
∞
∞
. Числитель и знаме-
натель дроби разделим на
3
x
:
3
23
3
3
24
1
24
lim lim
1
31
3
xx
xx
xx
x
1
3
x
→∞ →∞
+−
+− ∞
⎧⎫
== =
⎨⎬
+∞
⎩⎭
+
.
Пример 3.15. Вычислить
2
2
1
21
lim
54
x
x
x
xx
→−
+
+
+
+
.
Решение. Непосредственная подстановка значения
1
x
=
−
, дает неопреде-
ленность вида
0
0
⎧⎫
⎨⎬
⎩⎭
. Так как числитель и знаменатель многочлены, то их можно
разложить на множители. Тогда
22
2
111
21 0 (1) 10
lim lim lim 0
54 0 (1)(4) 43
xxx
xx x x
xx x x x
→− →− →−
++ + +
⎧⎫
== = ==
⎨⎬
++ + + +
⎩⎭
.
Пример 3.16. Вычислить
2
2
2
lim
53
x
x
x
→
−
+
−
.
Решение. Как и в предыдущем примере, здесь неопределенность вида
0
0
⎧⎫
⎨⎬
⎩⎭
. Раскроем неопределенность, умножив числитель и знаменатель дроби на
выражение, сопряженное выражению
(
)
2
53x
+
−
:
16
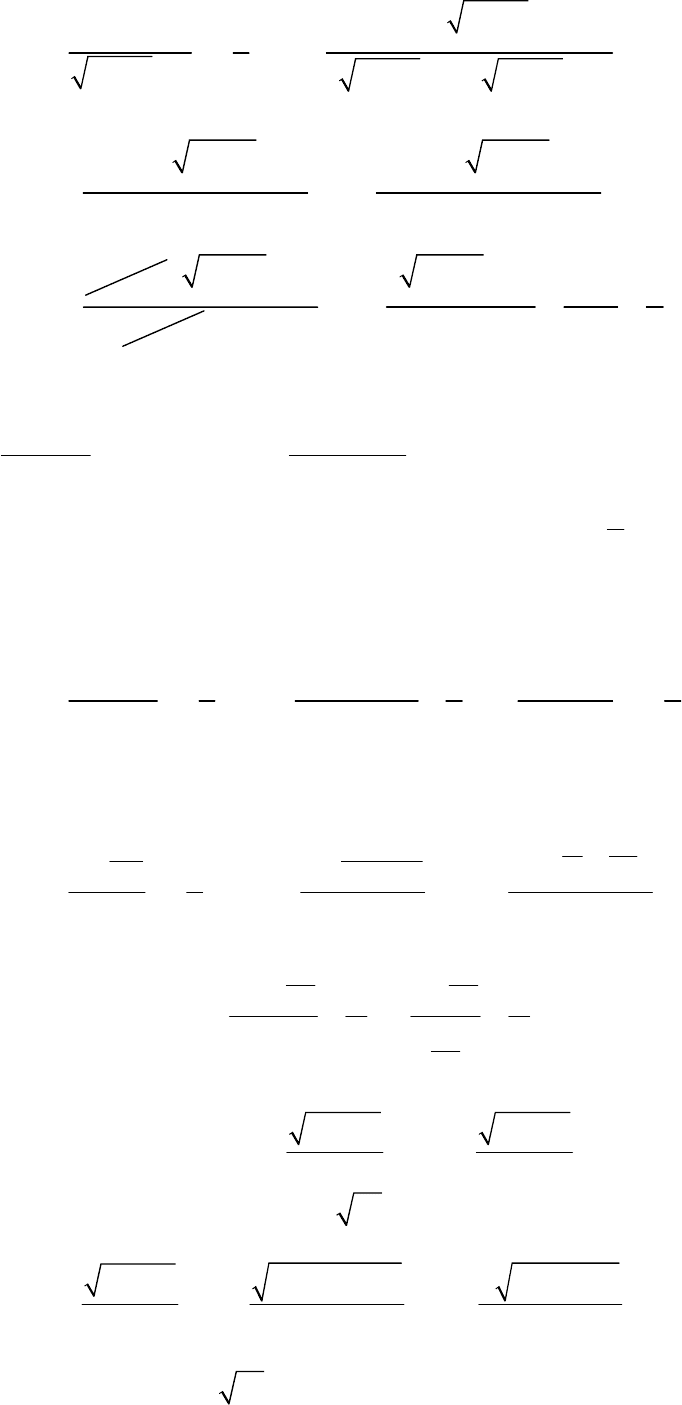
(
)
(
)
(
)
2
2
22
22
(2) 53
20
lim lim
0
53
53 53
xx
xx
x
x
xx
→→
−++
−
⎧⎫
=
==
⎨⎬
⎩⎭
+−
+− ++
(
)
(
)
22
22
22
(2) 53 (2) 53
lim lim
59 4
xx
xx xx
xx
→→
−++ −++
===
+− −
2
(2)
lim
x
x
→
−
=
(
)
2
53
(2)
x
x
++
−
(
)
2
2
53
33 3
lim
24
(2)
x
x
x
x
→
++
+
2
=
==
+
+
.
Пример 3.17. Вычислить
1)
2
0
1cos
lim
x
x
x
→
−
; 2)
1
cos( / 2)
lim
1
x
x
x
π
→
−
.
Решение. Здесь для раскрытия неопределенности вида
0
0
⎧⎫
⎨⎬
⎩⎭
воспользуем-
ся первым замечательным пределом.
1)
2
2
22
000
1 cos 0 2sin ( / 2) 1 sin( / 2) 1
lim lim lim
02/
xxx
xxx
xxx
→→→
−
⎧⎫ ⎛ ⎞
== = =
⎨⎬
⎜⎟
⎩⎭ ⎝ ⎠
22
.
2) Пусть . Тогда
1tx=− 1
x
t
=
+
и при
0t → 1
x
→
. Следовательно,
100
(1)
cos
cos cos
0
22
22
lim lim lim
10
xtt
t
xt
xtt
π
π
ππ
→→→
⎛⎞
+
+
⎜⎟
⎧⎫
⎝⎠
==− =−
⎨⎬
−
⎩⎭
=
00
sin sin
22
lim lim
22
2
tt
tt
t
t
π
π
π
π
π
→→
−
=− = =
.
Пример 3.18. Вычислить
2
41
lim
1
x
x
x
→+∞
+
+
и
2
41
lim
1
x
x
x
→−∞
+
+
.
Решение. Если 0( )
x
x>→+∞, то
2
x
x
=
. Тогда
22 2
2
(4 1/ ) (4 1/ )
41
lim lim lim 2
1(11/)(11/)
xx x
xx x x
x
xxxxx
→+∞ →+∞ →+∞
++
+
==
++ +
=
.
Если 0( )
x
x<→−∞, то
2
x
x
=
−
. Тогда
17

22 2
2
(4 1/ ) (4 1/ )
41
lim lim lim 2
1(11/) (11/)
xx x
xx x x
x
xxxxx
→−∞ →−∞ →−∞
+−+
+
==
++ +
=−
.
Пример 3.19. Вычислить
2
1
24
lim
11
x
хх
→
⎛⎞
−
⎜⎟
−
−
⎝⎠
.
Решение. Имеем неопределенность вида
{
}
∞
−∞
. Преобразуем функцию,
стоящую под знаком предела, приводя дроби к общему знаменателю
{}
22
11
24 2(1)4
lim lim
11 1
xx
х
хх х
→→
+−
⎛⎞
−=∞−∞=
⎜⎟
−− −
⎝⎠
=
2
11
2( 1) 0 2
lim lim 1
10 1
xx
х
хх
→→
−
⎧⎫
===
⎨⎬
−+
⎩⎭
=
.
Пример 3.20. Вычислить
3
2
1
lim 1
x
x
x
→∞
⎛⎞
+
⎜⎟
⎝⎠
.
Решение. Для раскрытия неопределенности
{
}
1
∞
используем второй заме-
чательный предел:
{}
2
2
1
3
3
3
lim
0
22
11
lim 1 1 lim 1 1
x
x
xx
x
x
xx
ee
xx
→∞
⋅
⋅
∞
→∞ →∞
⎡⎤
⎛⎞ ⎛⎞
+== + ==
⎢⎥
⎜⎟ ⎜⎟
⎝⎠ ⎝⎠
⎢⎥
⎣⎦
=
.
Пример 3.21. Вычислить
0
ln(1 )
lim
31
x
x
x
→
+
−
.
Решение. Из равенства (3.2) имеем
0
31
lim ln 3
x
x
x
→
−
=
. Отсюда и равенства (3.1)
00
ln(1 ) 0 ln(1 ) 1 1
lim lim 1
31 0 31 ln3ln3
xx
xx
xxx
x
→→
++
⎧⎫ ⎡ ⎤
== ⋅ =⋅=
⎨⎬
⎢⎥
−−
⎩⎭ ⎣ ⎦
.
Пример 3.22. Вычислить односторонние пределы:
1)
10
2
lim
1
x
x
→±
−
; 2)
1/
0
1
lim
13
x
x→±
+
.
Решение. 1) Если
1
x
<
, то
10
x
−
<
и, следовательно,
10
2
lim
1
x
x
→−
=−∞
−
. Если
1
x
>
, то
10
x
−>
и, следовательно, и
10
2
lim
1
x
x
→+
=
+∞
−
.
18
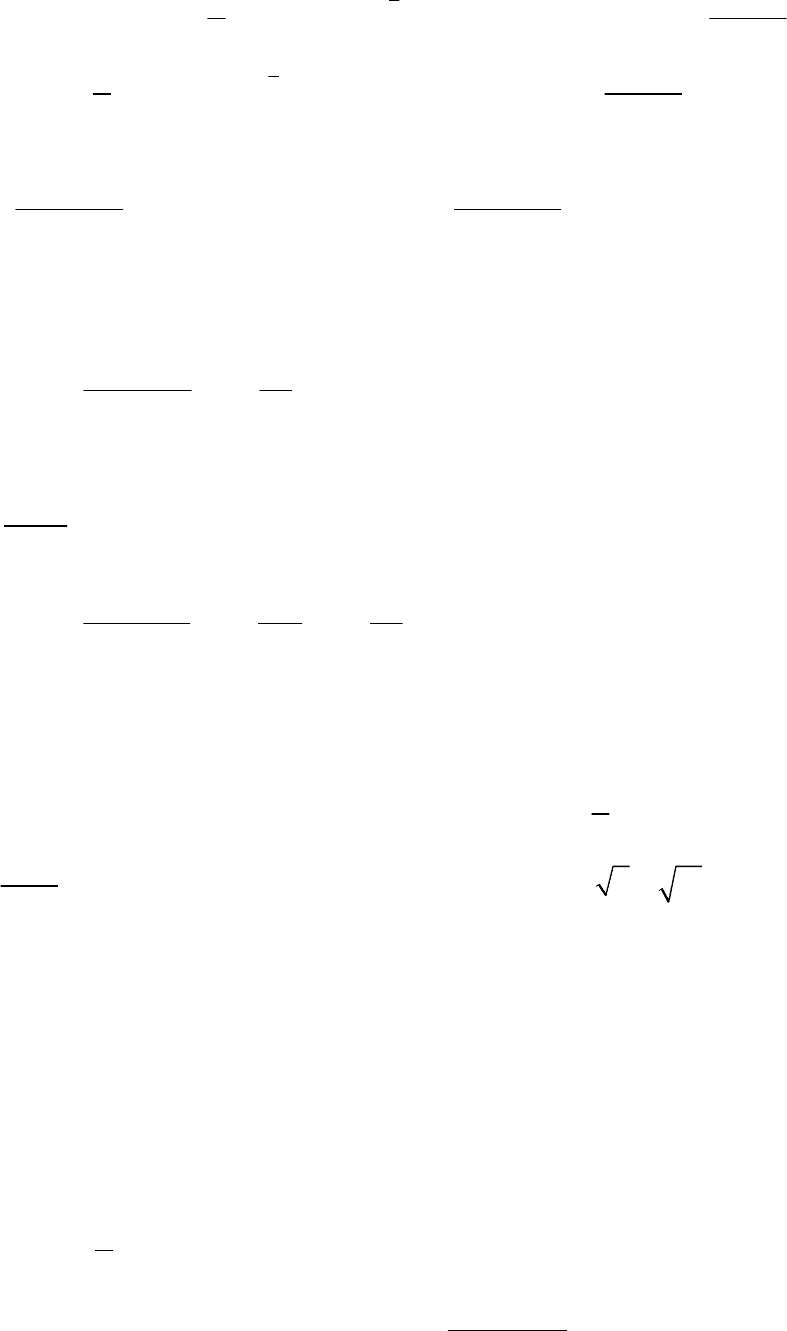
2) Если
0
x
<
, то
0
1
lim
x
x
→−
=
−∞ и
1
0
lim 3 0
x
x→−
=
. Следовательно,
1/
0
1
lim 1
13
x
x→−
=
+
.
Если
0
x
>
, то
0
1
lim
x
x
→+
=+∞ и
1
0
lim 3
x
x→+
=
+∞
. Следовательно,
1/
0
1
lim 0
13
x
x→+
=
+
.
Пример 3.23. С помощью принципа замены эквивалентных вычислить:
1)
0
sin 4
lim
ln(1 4 )
x
x
x
→
+
; 2)
0
1cos2
lim
tg3
x
x
x
→
−
.
Решение. 1) Имеем
sin 4 4
x
x∼
, ln(1 4 ) 4
x
x
+
∼ (см. таблицу эквивалентных
бесконечно малых функций). Тогда
00
sin 4 4
lim lim 1
ln(1 4 ) 4
xx
x
x
x
x
→→
==
+
.
2) Из таблицы эквивалентных бесконечно малых функций имеем:
2
2
(2 )
1cos2 2
2
x
x
x−=∼
, tg3 3
x
x∼ . Поэтому
2
000
1cos2 2 2
lim lim lim 0
tg3 3 3
xxx
xx x
xx
→→→
−
===
.
Задания для самостоятельного решения
3.23. Пользуясь определением предела функции в точке, доказать, что:
1)
; 2)
2
lim(3 2) 8
x
x
→
+=
0
lim(4 2 ) 4
x
х
→
+
=
; 3)
1
1
lim 1
x
х
→
= ;
4)
lim 1
2
x
х
х
→∞
=
−
; 5)
0
0
lim cos cos
xx
x
x
→
=
; 6)
0
0
lim
xx
x
x
→
=
.
3.24. Доказать, что функция
2
()
f
xx
=
при
0
x
→
является бесконечно
малой. При каких значениях переменной
x
значения функции будут отличаться
от нуля меньше, чем на: 1) 0,01; 2) 0,001.
3.25. Для функции () 2 3
f
xx
=
+ и заданного числа
0
ε
>
указать число
δ
такое, что для каждого
x
, удовлетворяющего условию
0| 3|
x
δ
<−<
. Справед-
ливо неравенство |(2 3) 9|
x
ε
+−<, если:
1)
1
ε
=
; 2)
0,5
ε
=
; 3)
0,01
ε
=
; 4)
0
ε
ε
=
.
3.26. Найти:
1)
2
1
1
lim 2 sin
x
x
x
x
π
→
⎛
+−
⎜
⎝⎠
⎞
⎟
; 2)
/2
lim (2 cos )
x
x
x
π
→
+
;
3)
2
2
lim((4 1) cos )
x
x
x
→
−
; 4)
2
1
21
lim
1
x
x
x
x
→
−
+
+
;
19
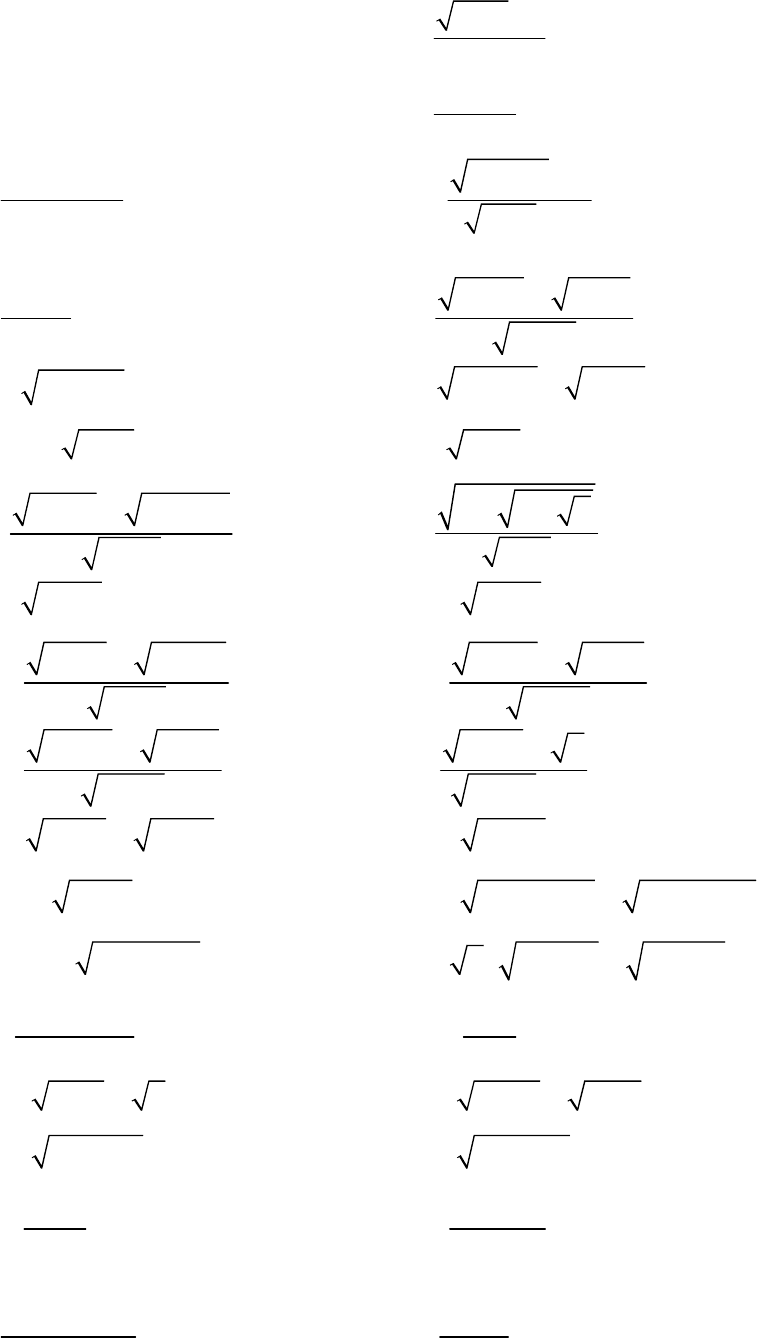
5)
10
2
lim(3 )
x
x
→
−
; 6)
1
31
lim
2
x
x
x
→
+
−
+
;
7)
; 8)
2
2
lim(2 2 1)
x
xx
→
−+
3
8
2
2
lim
(1)
x
x
x
→
+
−
;
9)
2
2
1
3
lim
4
x
xx
x
→
−+
−
4
; 10)
2
1
8
lim
35
x
x
xx
x
→
+
−
+
+
.
3.27. Найти:
1)
2
2
1
lim
2
x
x
x
→∞
+
+
; 2)
23
3
4
4
21
lim
8
x
xx
x
→−∞
+
−−
+
;
3)
(
)
lim ( 1)
x
x
x
→+∞
+−x; 4)
(
)
22
lim 2 1
x
xxx
→∞
+
−+
;
5)
(
lim 5
x
xx
→+∞
++
)
; 6)
(
)
lim 2
x
x
x
→+∞
+
− ;
7)
24
4
5
5
381
lim
1
x
xx
x
→±∞
++ +
−
1
; 8) lim
1
x
x
xx
x
→+∞
++
+
;
9)
(
)
2
lim 1
x
x
x
→+∞
+−
; 10)
(
)
2
lim 1
x
x
x
→−∞
+
+
;
11)
23
3
3
3
18
lim
1
x
xx
x
→−∞
−− +
−
1
; 12)
23
3
4
4
21
lim
8
x
xx
x
→−∞
+
−−
+
;
13)
23
3
4
4
2
lim
8
x
xx
x
→+∞
+− −
+
1
; 14)
2
3
4
1
lim
x
x
x
x
xx
→∞
+−
+
−
;
15)
(
)
22
lim 1 1
x
xx
→∞
−− +
; 16)
(
)
2
lim 2
x
x
x
→±∞
−
−
;
17)
(
)
2
lim 1
x
x
x
→±∞
+−x
; 18)
(
)
22
lim 2 1 5 1
x
xx xx
→±∞
−
−− − +
;
19)
(
)
2
lim 3
x
xxx
→±∞
−++
; 20)
(
)
22
3
33
lim ( 1) ( 1)
x
xx x
→+∞
+− −
;
21)
2
2
7
lim
3
x
x
1
x
x
x
→∞
−+
⋅
; 22)
lim arcctg
1
x
x
x
x
→±∞
⎛⎞
+
⎜⎟
+
⎝⎠
;
23)
lim ( 5 )
x
х
х
→+∞
+− ; 24) lim ( 2 1 2)
x
хх
→+∞
+
−+;
25)
2
lim ( 10 )
x
х
хх
→±∞
+−; 26)
2
lim ( 4 3 2 )
x
х
хх
→+∞
+− ;
27)
31
lim
3
х
х
x→±∞
+
−1
; 28)
25 3
lim
95 4
х
х
x→±∞
⋅
−
⋅
+
.
3.28. Найти:
1)
32
2
0
2
lim
x
xx
х
x
х
→
−+
+
; 2)
2
2
4
lim
2
x
x
x
→−
−
+
;
20
