Rudnick L. Lubricant Additives: Chemistry and Applications (Присадки, добавки к смазкам)
Подождите немного. Документ загружается.


544 Lubricant Additives: Chemistry and Applications
The vapor-phase rotational entropy is given by [44]
SR
q
IRT
h
a
vap,rot
i
⫽⫹1
18
3
2
ln
/
p
2
(22.17)
Here
a
= number of independent rotation axes
q = degeneracy
I = moment of inertia
An approximation for S
i
vap,rot
is given in Ref. 40.
The vaporization entropy also includes the vibrational entropy. The available vibrational
states are comparable between liquid and vapor for these high-molecular-weight hydrocarbons or
polymeric oil molecules, whereas the translational and rotational states are much more restricted
in the liquid phase.
Note that the ideal gas law is employed in deriving Equation 22.15. The vaporization enthalpy
∆H
i
vap
= ∆E
i
vap
+ ∆(PV)
i
. The pressure volume expansion work term has been replaced by ∆(PV)
i
=
RT. The vaporization activation energy, ∆E
i
vap
, also depends on molecular weight because a longer
molecule requires more energy to overcome the intermolecular interaction force between itself and
its neighbors in the surrounding liquid. Polar end groups contribute a xed amount to the vapor-
ization energy, which accounts for the intercept in the plot of vaporization energy as a function of
molecular weight. As one might expect, there is a linear relation between the activation energy and
molecular weight for Zdol [45], ∆E
i
vap
≈ ∆E
int
+ ∆E
slope
× M
i
. The slope, ∆E
slope
= 0.029 kJ/mol/Da,
and intercept, ∆E
int
= 50 kJ/mol, of the vaporization activation energy dependence on molecular
weight for Zdol were determined by comparing the simulated evaporation data with that measured
by isothermal TGA. The thermodynamic properties, vapor-phase diffusion coef cient, and vapor
pressure for a range of ideal monodisperse Zdol molecular weights calculated as described earlier
are listed in Table 22.9 [1]. The numerical values in Table 22.9 can be used in Equation 22.15 to
calculate the vapor pressure of perfectly monodispersed molecular weight fractions.
Actual samples of commercial PFPE lubricant such as Zdol are polydisperse. Consequently, there
is a wide range of partial pressures for a given sample, and the lowest molecular weight species in the
distribution have the highest vapor pressure. In the case of Zdol 2000, because it is a copolymer of
per uoromethylene and per uoroethylene oxide, the lowest molecular weight oligomers group together
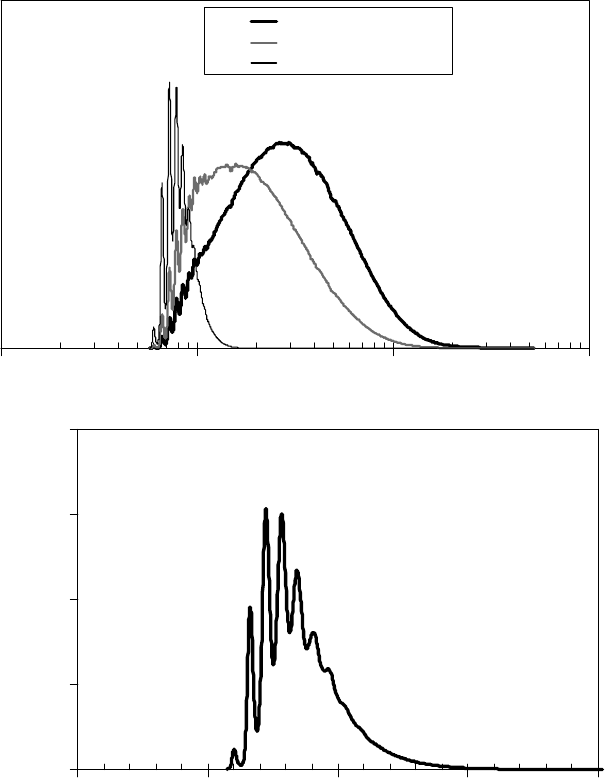
with similar molecular weights, hence similar vapor pressures. Figure 22.13a [1] shows the molecular
weight distribution of Zdol 2000 measured by GPC. The oscillations in the molecular weight distribu-
tion are visible up through 1000 Da. The mole fraction distribution is also shown, as it plays a key role
in determining the actual vapor pressure. Qualitatively, the vapor pressure increases with decreasing
molecular weight, but as the molecular weight becomes lower, there are fewer of these molecules in the
solution, so Raoult’s law acts to partly offset the increase in vapor pressure, causing the vapor pressure
to decrease in the limit of low molecular weight. Hence, the shape of the partial pressure distribution
superimposed on the distribution in Figure 22.13a, calculated at 50°C. The partial pressure distribu-
tion for Zdol is shown with units on an expanded scale in Figure 22.13b. This shows the great detail
provided by the GPC method, and also, the partial pressure peaks show the molecular weights that will
evaporate with the highest rate or distill out of the distribution. The total vapor pressure of polydisperse
Zdol 2000 at 50°C is the sum of the partial pressures of each component, in this case, 0.2 Pa.
There are some other important properties of magnetic recording disk lubricants that will not
be covered in this chapter, and several references on these are provided later. Lubricant spin-off and
transfer to the slider is minimized by chemisorption to the overcoat [46]. Chemisorption [47], also
referred to as bonding, is well described by Tyndall et al. [48]. Disk lubricants also serve to inhibit
CRC_59645_Ch022.indd 544CRC_59645_Ch022.indd 544 3/20/2009 5:44:29 PM3/20/2009 5:44:29 PM

Lubricants for the Disk Drive Industry 545
corrosion. The corrosion protection ability of Zol lubricants was related to surface energy by Tyn-
dall et al. [48] The most successful disk lubricant additive has been cyclic phosphazines. However,
cyclic phosphazine increases the lubricant mobility [49] and decreases the dewetting thickness [37].
More recently, an effort has been made to combine the desirable properties of both by incorporating
a cyclic phosphazine end group onto Zdol. This lubricant is referred to as A20H, and it is described
by Waltman et al. [5]. The A20H end group is shown in Table 22.1.
TABLE 22.9
Vaporization Entropy ∆S
i
vap
, Binary Diffusion Coeffi cient D
i
, and Vapor
Pressure P
i
vap
for Perfectly Monodispersed Zdol Fractions Evaporating into
Nitrogen at Ambient Pressure (10
5
Pa) at Three Different Temperatures,
S
liq
= 107 J/mol K, ∆E
i
vap
= 50 + 0.029 × M
i
M
i
(Da)
∆S
i
vap
(J/mol K)
D (m
2
/s) P
i
vap
(Pa)
Temperature 35°C
500 123 3.16 × 10
−6
1.13 × 10
0
750 133 2.27 × 10
−6
2.26 × 10
−1
1000 140 1.78 × 10
−6
3.17 × 10
−2
1350 147 1.38 × 10
−6
1.48 × 10
−3
1500 150 1.26 × 10
−6
3.72 × 10
−4
2000 157 9.79 × 10
−7
3.07 × 10
−6
3000 167 6.82 × 10
−7
1.25 × 10
−10
4000 174 5.25 × 10
−7
3.61 × 10
−15
4300 176 4.91 × 10
−7
1.50 × 10
−16
5400 182 3.98 × 10
−7
1.16 × 10
−21
Temperature 45°C
500 123 3.32 × 10
−6
2.76 × 10
0
750 133 2.38 × 10
−6
6.01 × 10
−1
1000 141 1.87 × 10
−6
9.19 × 10
−2
1350 148 1.44 × 10
−6
4.87 × 10
−3
1500 151 1.32 × 10
−6
1.29 × 10
−3
2000 158 1.02 × 10
−6
1.27 × 10
−5
3000 168 7.15 × 10
−7
7.44 × 10
−10
4000 175 5.51 × 10
−7
3.05 × 10
−14
4300 177 5.15 × 10
−7
1.41 × 10
−15
5400 183 4.18 × 10
−7
1.61 × 10
−20
Temperature 60°C
500 124 3.56 × 10
−6
9.51 × 10
0
750 135 2.55 × 10
−6
2.34 × 10
0
1000 142 2.00 × 10
−6
4.05 × 10
−1
1350 149 1.55 × 10
−6
2.55 × 10
−2
1500 152 1.41 × 10
−6
7.28 × 10
−3
2000 159 1.10 × 10
−6
9.19 × 10
−5
3000 169 7.66 × 10
−7
8.80 × 10
−9
4000 176 5.90 × 10
−7
5.91 × 10
−13
4300 178 5.52 × 10
−7
3.17 × 10
−14
5400 184 4.48 × 10
−7
6.26 × 10
−19
Note: Other parameters used are given in the text.
Source: Adapted from Rudnick, L.R. (ed.), Synthetics, Mineral Oils, and Bio-Based Lubricants Chemis-
try and Technology, Chapter 38, CRC Press, Taylor & Francis Group, Boca Raton, FL, 2006.
CRC_59645_Ch022.indd 545CRC_59645_Ch022.indd 545 3/20/2009 5:44:29 PM3/20/2009 5:44:29 PM
546 Lubricant Additives: Chemistry and Applications
22.3 SPINDLE MOTOR LUBRICANTS
There are ball bearing and uid dynamic bearing spindle motors (see Ref. 50 for a good overview). The
arrangement of the spindle motor and types of spindle motor bearing are shown in Figure 22.14 [1].
22.3.1 BALL BEARING SPINDLE MOTOR BEARING GREASE
Ball bearing spindle motor bearings are typically lubricated with an NLGI grade 2 lithium grease.
The grease composition, referred to as SRL, is a lithium grease comprising approximately 10% Li
12-hydroxy stearate, 17% di-2-ethylhexyl sebacate, and 70% pentaerythritol tetraesters, and the
rest is a sulfonate rust inhibitor and an amine antioxidant. Lithium soap gel bers thicken the
100 1000 10,000 100,000
Molecular weight (Da)
Weight fraction
Mole fraction
Partial pressure
(a)
0.0000
0.0005
0.0010
0.0015
0.0020
0 500 1000 1500 2000
Molecular wei
g
ht
(
Da
)
Partial pressure (Pa)
(
b
)
FIGURE 22.13 The molecular weight distribution, mole fraction distribution, and the calculated partial
pressure distribution (a), and the partial pressure distribution on an expanded scale with units (b) for Zdol
2000 at 50°C. (Adapted from Rudnick, L.R. (ed.), Synthetics, Mineral Oils, and Bio-Based Lubricants Chem-
istry and Technology, Chapter 38, CRC Press, Taylor & Francis Group, Boca Raton, FL, 2006.)
CRC_59645_Ch022.indd 546CRC_59645_Ch022.indd 546 3/20/2009 5:44:29 PM3/20/2009 5:44:29 PM

Lubricants for the Disk Drive Industry 547
grease [51,52]. The grease base oil viscosity at 40°C is 22 mPa s, and the worked penetration is 245.
A great variety of greases could potentially be used in these bearings, but in practice, the grease is
limited by stringent requirements of low volatility, yield stress at temperature, low torque noise, and
good thermal stability.
22.3.1.1 Yield Stress at Temperature
Typical ball bearing spindle motor grease rheological properties and yield stress are described by
Karis et al. [53]. For practical purposes, the yield stress is measured by gradually increasing the
stress in a stress rheometer with a cone-plate xture. The yield stress is detected when the cone
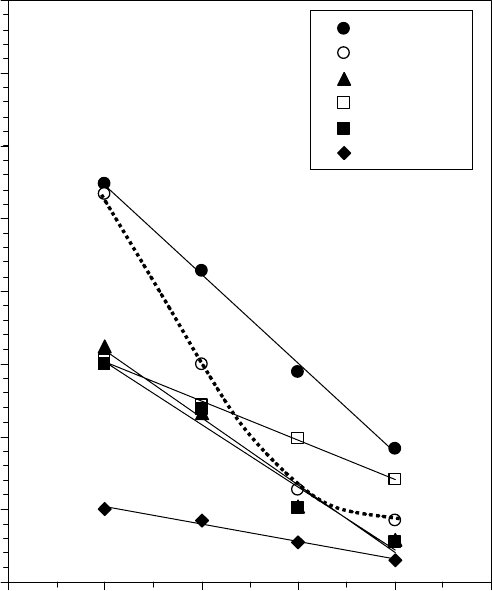
begins to rotate. For example, the yield stress as a function of temperature for several grease can-
didates for use in ball bearing spindle motors is shown in Figure 22.15 [1]. There is a general trend
Disk
Spindle
motor
Suspension
Base casting
Ball bearing spindle motor
Fluid bearing spindle motor
Slider
Stator
Rotor
Fluid
bearings
(a)
(c)
Ferrofluid seal
Stator
Rotor
Ball
bearings
(b)
FIGURE 22.14 The arrangement of the magnetic recording disks and head suspension assembly on the
spindle motor (a), schematic ball bearing spindle motor (b), and schematic uid bearing spindle motor (c).
(Adapted from Rudnick, L.R. (ed.), Synthetics, Mineral Oils, and Bio-Based Lubricants Chemistry and Tech-
nology, Chapter 38, CRC Press, Taylor & Francis Group, Boca Raton, FL, 2006.)
CRC_59645_Ch022.indd 547CRC_59645_Ch022.indd 547 3/20/2009 5:44:30 PM3/20/2009 5:44:30 PM
548 Lubricant Additives: Chemistry and Applications
of decrease with temperature, but all the greases maintain a measurable yield stress up through at
least 80°C. The decrease of the yield stress with temperature is much less than that of the grease
base oil, as will be shown later.
Diluting the grease with additional base oil, or incorporation of contaminants in the grease,
also affects the yield stress. Additional oil is often added to prelubricate the new bearing once it has
been lled with grease. This is done to provide a lubrication lm during initial start-up of the new
bearing, before the base oil from the gel thickener of the grease has had time to diffuse throughout
the surfaces of the balls and raceways. The prelube can either be the grease base oil itself or spe-
cially formulated prelube oil. Results with two types of prelube are also described here. Prelube
oil A is diester oil with a sulfonate rust inhibitor and a hindered phenol antioxidant. Prelube oil B
is mostly diester oil with several percent of poly alpha ole n oil, a sulfonate rust inhibitor, and a
Zn dialkyldithocarbamate antiwear additive. Grease may also be exposed to organometallic salts
formed from various components within the bearing, bearing shields, or motor. Zn was incorpo-
rated as Zn(diacrylate), and Fe was incorporated as iron (III) 2-ethylhexanoate. The Zn(diacrylate)
contaminant was intended to model products of bearing corrosion by the incomplete curing of a
motor bearing adhesive [54].
Model grease containing prelube or contaminants was prepared in the laboratory by thor-
oughly mixing them in a custom-built lab-scale grease mill. The grease mill capacity was ∼10 g
of grease. The mill comprised two 32 mm diameter disks perforated with 35 circular holes,
0
100
200
300
400
500
600
700
800
0 20 40 60 80 100
Temperature (°C)
Yield stress (Pa)
F4
SRL
L252
BQ 72-72
LY
716R
FIGURE 22.15 The yield stress of various candidate greases for ball bearing spindle motors as a function of
temperature. (Adapted from Rudnick, L.R. (ed.), Synthetics, Mineral Oils, and Bio-Based Lubricants Chem-
istry and Technology, Chapter 38, CRC Press, Taylor & Francis Group, Boca Raton, FL, 2006.)
CRC_59645_Ch022.indd 548CRC_59645_Ch022.indd 548 3/20/2009 5:44:30 PM3/20/2009 5:44:30 PM
Lubricants for the Disk Drive Industry 549
each 460 µm in diameter, inside a stainless steel tube. The perforated disks were separated by a
3.8 mm wide cavity. Grease was forced back and forth through the holes in the perforated disks
by the reciprocating action of two opposing pneumatic cylinders driving Te on pistons against the
perforated plate within the steel tube. Air pressure was alternately applied to the cylinders using a
cam and follower arrangement driven by a variable speed gear motor.
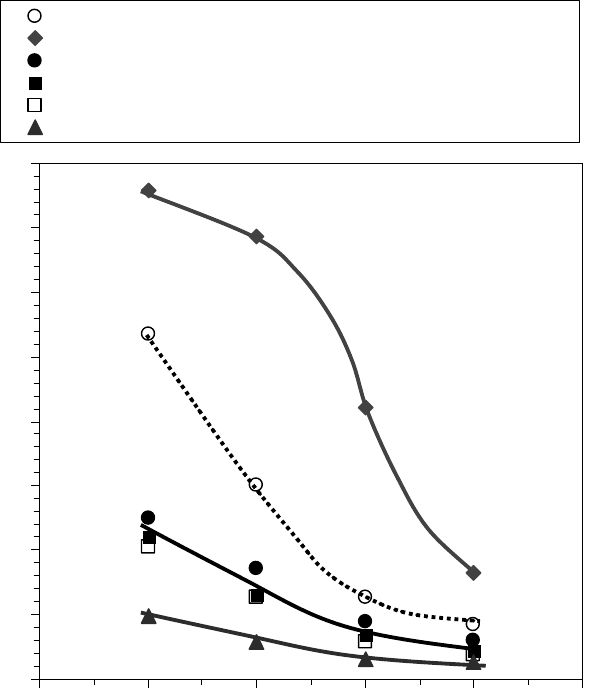
The yield stress of these model greases is shown in Figure 22.16 [1]. The yield stress was
increased by Zn(diacrylate), whereas prelube oils decreased the yield stress.
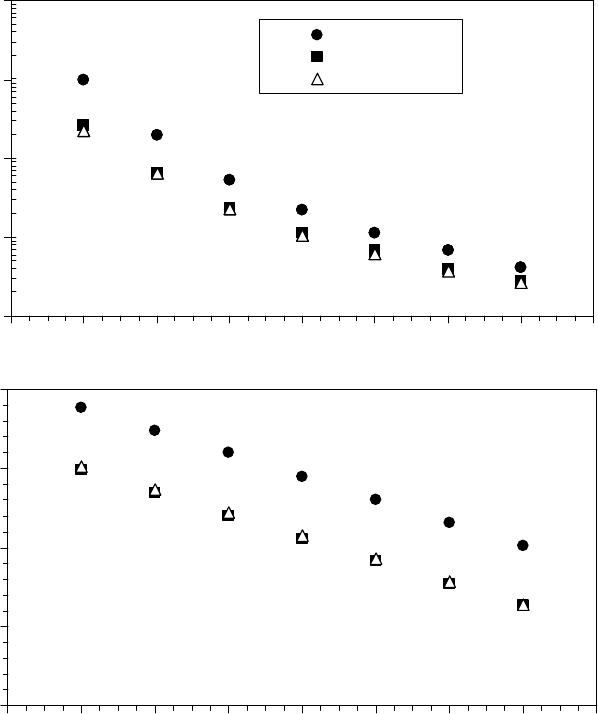
For comparison with the yield stress versus temperature, the viscosity and density of the SRL
grease base oil and two prelube oils are shown as a function of temperature in Figure 22.17 [1]. The
viscosity and density of the base oil are somewhat higher than that of the prelube oils. Blends between
the base oil and the prelube oil A or B will have intermediate viscosities. The oil viscosity decreases
much more than the yield stress with temperature. This implies that most of the yield stress change with
temperature (Figure 22.16) is due to the gel network of the thickener. The reduction in yield stress on
blending grease with prelube oil is probably due to dilution of a transient network in the gel thickener.
0
100
200
300
400
500
600
700
800
0 20 40 60 80 100
Temperature (°C)
Yield stress (Pa)
Base grease
+0.6% Zn(diacrylate)
+12.5% base oil
+16% Prelube A
+16% Prelube B
+36% Prelube B + 0.03% Zn(diacrylate) + 0.01% Fe(octanoate)
FIGURE 22.16 The yield stress of base grease SRL showing the effect of additional base oil, prelube oils,
and organometallic salt contamination on yield stress as a function of temperature. (Adapted from Rudnick,
L.R. (ed.), Synthetics, Mineral Oils, and Bio-Based Lubricants Chemistry and Technology, Chapter 38, CRC
Press, Taylor & Francis Group, Boca Raton, FL, 2006.)
CRC_59645_Ch022.indd 549CRC_59645_Ch022.indd 549 3/20/2009 5:44:30 PM3/20/2009 5:44:30 PM
550 Lubricant Additives: Chemistry and Applications
22.3.1.2 Hydrodynamic Film Thickness
The hydrodynamic lm thickness of the oil provided by the grease must be suf cient to clear the
asperities on the balls and race during operation at the speci ed load and velocity. The hydrodynamic
lm thickness is given by
hkU
p
⫽ ()()
..
0
067 053
(22.18)
where
h = lm thickness
k = material and geometry parameter
U = entrainment velocity
η
0
= viscosity at atmospheric pressure
α
p
= pressure–viscosity coef cient [55]
−40 −20 0 20 40 60 80 100 120
Temperature (
°C)
Viscosity (Pa s)
Base oil
Prelube A
Prelube B
(a)
800
850
900
950
1000
−40 −20 0 20 40 60 80 100 12
0
Temperature (°C)
Density (kg/m
3
)
(b)
1.0×10
1
1.0×10
0
1.0×10
−1
1.0×10
2
1.0×10
3
FIGURE 22.17 The viscosity (a) and density (b) of SRL grease base oil and two prelube oils as a function of
temperature. (Adapted from Rudnick, L.R. (ed.), Synthetics, Mineral Oils, and Bio-Based Lubricants Chem-
istry and Technology, Chapter 38, CRC Press, Taylor & Francis Group, Boca Raton, FL, 2006.)
CRC_59645_Ch022.indd 550CRC_59645_Ch022.indd 550 3/20/2009 5:44:31 PM3/20/2009 5:44:31 PM
Lubricants for the Disk Drive Industry 551
The lm thickness between a steel ball and a plate by ultrathin- lm interferometry [56] was
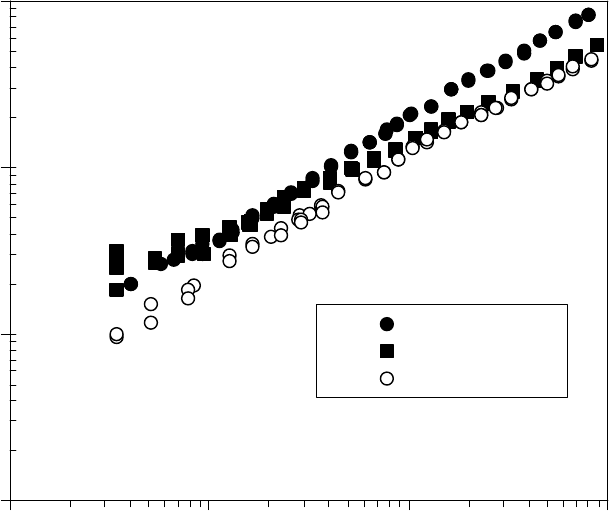
measured by Professor H.A. Spikes, and his students, at Imperial College in London. The lm thick-
ness as a function of sliding speed for the grease base oil, and the prelube oils A and B, is shown
in Figure 22.18 [1]. There is some variation in the power law slope between the oils, which slightly
varies from the coef cients used in Equation 22.18. By comparison with a uid with a known pres-
sure–viscosity coef cient, they estimated the pressure–viscosity coef cients over a limited speed
range between 0.1 and 1 m/s to be ∼15 1/GPa for the base oil, 12 1/GPa for prelube oil A, and
10.5 1/GPa for prelube oil B. The difference between prelube oils A and B is probably due to the
minor fraction of polyalphaolephin in prelube oil B.
22.3.1.3 Grease Electrochemistry
Some types of high-performance disk drive spindle motors incorporate ball bearings with silicon
nitride ceramic balls for higher stiffness and lower vibration. It is critical that the bearings and grease
provide smooth rotation so as not to excite resonances of the disk pack (Figure 22.14a). Electrostatic
potential generated by bearings can induce a small current ow through the bearing, with a return path
through the ferro uid seal (Figure 22.14b). To investigate the effect of electrochemistry, grease con-
taining various types of contaminants was sandwiched between two steel electrode plates. The plates
were made of 25 mm diameter mirror polished 304 stainless steel disks with grease in between them
on a 160 µm thick lter paper. The plates were subjected to 25 V to simulate the passage of electrical
current through the grease in the bearing. After several hundred hours, the plates were separated and
examined for degraded grease as deposits on the plates. Film deposits were characterized by optical
microscopy, FTIR spectroscopy in re ection, and x-ray photoelectron spectroscopy (XPS).
0.10
1.00
10.00
100.00
0.001 0.010 0.100 1.000
Mean rollin
g
s
p
eed
(
m/s
)
Film thickness (nm)
Base oil
Prelube A
Prelube B
FIGURE 22.18 The lm thickness as a function of rolling speed measured by ultrathin- lm interferometry.
(Adapted from Rudnick, L.R. (ed.), Synthetics, Mineral Oils, and Bio-Based Lubricants Chemistry and Tech-
nology, Chapter 38, CRC Press, Taylor & Francis Group, Boca Raton, FL, 2006.)
CRC_59645_Ch022.indd 551CRC_59645_Ch022.indd 551 3/20/2009 5:44:31 PM3/20/2009 5:44:31 PM
552 Lubricant Additives: Chemistry and Applications
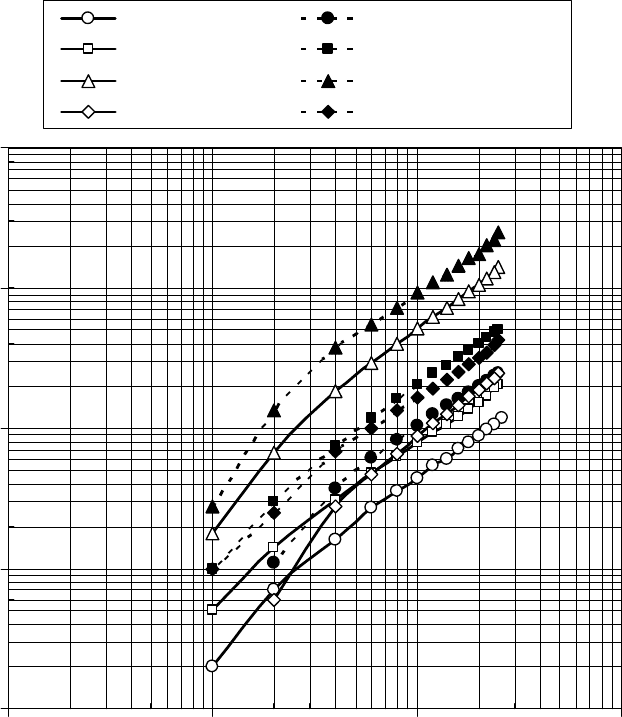
Figure 22.19 [1] shows the current through the electrode plates plotted as a function of the voltage
applied across the grease lm with fresh grease between the plates. The conductance of the ferro uid
seal in the motor was ∼77 nS (13 MΩ), so that the current through the bearing is typically 30–80 nA.
In steady state, the electrochemical cells were operated at 25 V, or between 100 and 3000 nA, depend-
ing on the type of grease contamination. The higher voltage was employed in the electrochemical
cells to increase the rate of any electrochemical reactions that might take place. The initial conduc-
tance of the electrochemical cells, calculated from the linear region of the current–voltage plot, is
listed in the second column of Table 22.10 [1]. The lowest conductance was obtained with the SRL
grease alone, and SRL grease combined only with an additional 12.5% more of its own base oil. The
highest conductances were found with the grease containing 16% prelube oil B and 300 ppm Zn,
and grease containing 16% prelube oil B. The grease conductance gradually varied with time during
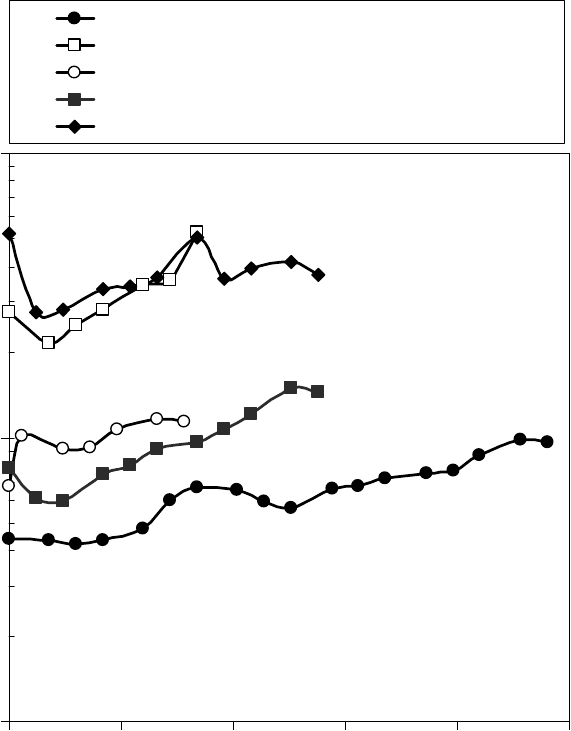
voltage application, as shown for several greases with and without contaminants in Fig ure 22.20.
The pure grease, with no diluents or contaminants, maintained the lowest conductance.
1
10
100
1,000
10,000
0.1 1 10 100
Voltage (VDC)
Current (nA)
SRL grease alone 300 ppm Zn
16% Prelube A 16% Prelube A + 300 pm Zn
16% Prelube B 16% Prelube B + 300 ppm Zn
12.5% Base oil 12.5% Base oil + 300 ppm Zn
FIGURE 22.19 Initial current–voltage plot for SRL grease alone, and SRL grease with the indicated
additives and contaminants measured in the electrochemical cells. (Adapted from Rudnick, L.R. (ed.), Syn-
thetics, Mineral Oils, and Bio-Based Lubricants Chemistry and Technology, Chapter 38, CRC Press, Taylor
& Francis Group, Boca Raton, FL, 2006.)
CRC_59645_Ch022.indd 552CRC_59645_Ch022.indd 552 3/20/2009 5:44:31 PM3/20/2009 5:44:31 PM
Lubricants for the Disk Drive Industry 553
After several hundred hours, the plates were separated and washed with chloroform by squirting
from a pipette. When present, lms were observed on the negative electrode plate. Although there
was sometimes minor lm formation or slight pitting on the positive plate, there was too little to
quantify. Micrographs of the lm deposits on several of the negative electrode plates are shown in
Figure 22.21 [1]. These show the brous appearance. The lm deposits were highly viscous. Film
deposits were qualitatively ranked in terms of their severity, which is referred to as light, medium,
and heavy, after the indicated electrolysis time (Table 22.10). The lightest deposits were observed
with the virgin grease, and the grease diluted with its own base oil. The heaviest deposit coincided
with the highest conductance. However, although they had nearly the lowest conductance, grease
contaminated by 300 ppm of Zn as acrylate, or with 16% of the prelube oil A, also formed heavy
deposits.
Re ection FTIR was performed on the residue on the plates after each test. Typical FTIR
spectra are shown in Figure 22.22 [1]. The IR peaks were assigned to chemical groups according to
1
10
100
0 200 400 600 800 100
0
Time (h)
Conductance (nS)
SRL grease alone
36% Prelube A + 300 ppm Zn +100 ppm Fe
300 ppm Zn
16% Prelube A
16% Prelube B
FIGURE 22.20 Conductance–time plot for SRL grease alone, and SRL grease with additives and
contaminants measured in the electrochemical cells. (Adapted from Rudnick, L.R. (ed.), Synthetics, Mineral
Oils, and Bio-Based Lubricants Chemistry and Technology, Chapter 38, CRC Press, Taylor & Francis Group,
Boca Raton, FL, 2006.)
CRC_59645_Ch022.indd 553CRC_59645_Ch022.indd 553 3/20/2009 5:44:31 PM3/20/2009 5:44:31 PM
