Rudnick L. Lubricant Additives: Chemistry and Applications (Присадки, добавки к смазкам)

Подождите немного. Документ загружается.

534 Lubricant Additives: Chemistry and Applications

22.2.1.3 Thin Film Viscosity

The aforementioned results have shown that in bulk PFPE disk lubricants, viscosity increases

exponentially as the measurement temperature approaches the glass transition temperature. This is

because chain motions are progressively frozen out as the thermal energy becomes less than their

activation energy. The lubricant viscosity also increases as the lubricant  lm thickness decreases,

which helps to prevent the lubricant from  owing completely off of the magnetic recording disks in

the air shear [32]. Viscosity enhancement of thin  lms arises from a different mechanism than that

found with decreasing temperature.

Dispersive interaction has a dramatic effect on the viscosity of the molecular layers closest

to the surface, which can be explained in terms of the rate theory for viscous  ow. Within the

Demnum S100

(a)

Krytox 143AD

Demnum SA2

Krytox COOH

(b)

Demnum S100

Krytox 143AD

Demnum SA2

Krytox COOH

1×10

−16

1×10

−2

1×10

−4

1×10

−14

1×10

−12

1×10

−10

1×10

−8

1×10

−6

1×10

−4

1×10

−2

1×10

−16

1×10

−2

1×10

−4

1×10

−14

1×10

−12

1×10

−10

1×10

−8

1×10

−6

1×10

−4

1×10

−2

1×10

G′′ (Pa)G′ (Pa)

ωa

(rad/s)

ωa

(rad/s)

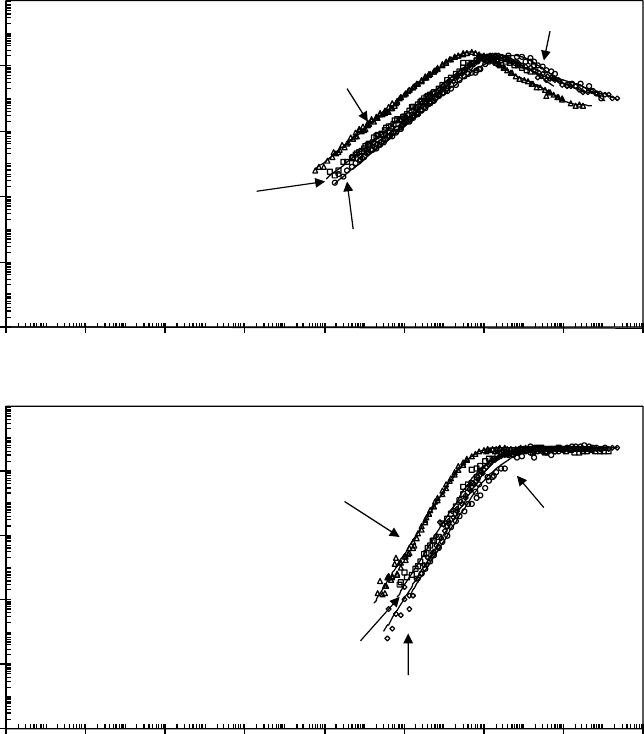
FIGURE 22.6 Shear loss (a) and storage (b) modulus master curves for the Demnum and Krytox series. The

smooth curves are from the discrete relaxation time series  t to the frequency–temperature shifted data. Ref-

erence temperature is T

. (Adapted from Rudnick, L.R. (ed.), Synthetics, Mineral Oils, and Bio-Based Lubri-

cants Chemistry and Technology, Chapter 38, CRC Press, Taylor & Francis Group, Boca Raton, FL, 2006.)

CRC_59645_Ch022.indd 534CRC_59645_Ch022.indd 534 3/20/2009 5:44:25 PM3/20/2009 5:44:25 PM

Lubricants for the Disk Drive Industry 535

rate theory, a  ow event comprises the transition of a  ow unit from its normal or quiescent state,

through a  ow-activated state, to a region of lower free energy in an external stress  eld. For small

molecules, the  ow unit is the whole molecule, whereas for longer chains, the  ow unit is a segment

of the whole molecule. By analogy with chemical reaction rate theory, there is a  ow activation

enthalpy, ∆H

vis

, and entropy, ∆S

vis

, for transition into the  ow-activated state.

A  ow unit is approximated by a particle in a box, with the energy being partitioned among

rotational and translational degrees of freedom, which govern the transition probability. On this

basis, the viscosity η = (Nh

) exp (∆G

vis

/RT), where N is Avogadro’s number, h

the Planck’s

constant, V

the molar volume, R the universal gas constant, T the temperature, and ∆G

vis

∆H

vis

− T∆S

vis

the  ow activation Gibbs free energy. The  ow activation enthalpy ∆H

vis

= ∆E

vis

+ ∆(pV)

vis

, where ∆E

vis

is the  ow activation energy and ∆(pV)

vis

the pressure–volume work. At

constant pressure, ∆(pV) = p∆V

vis

. For PFPE Z, the  ow activation volume ∆V

vis

≈ 0.1 nm

[17],

Z03

Zdiac

Zdeal

Ztetraol 2000

Ztx

Zdol 2500

Relaxation time (s)

0.8 1.2 1.4 1.6 1.8

m/n

Relaxation time (s)

1×10

−4

1×10

−5

1×10

−6

1×10

−4

1×10

−5

1×10

−6

(a)

(

)

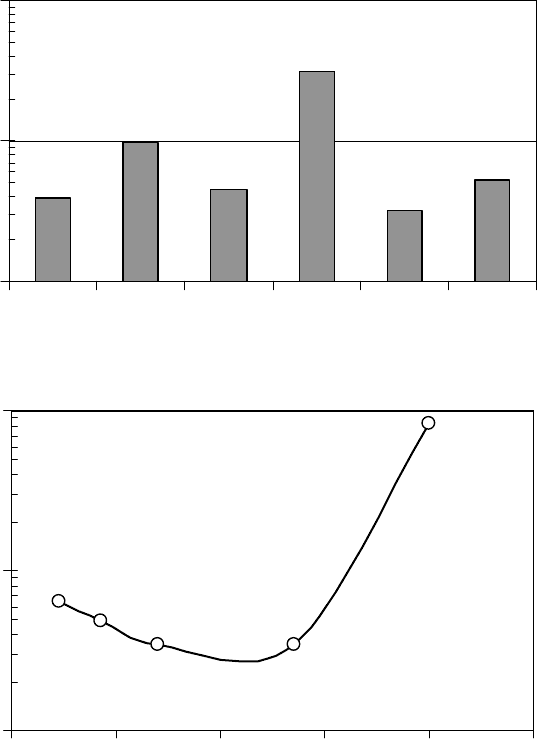
FIGURE 22.7 Longest relaxation time at 50°C for the Z series of lubricants (a) and Zdo14K series with a

range of monomer chain composition (b) calculated from the dynamic rheological measurements with time–

temperature superposition. (Adapted from Rudnick, L.R. (ed.), Synthetics, Mineral Oils, and Bio-Based Lubri-

cants Chemistry and Technology, Chapter 38, CRC Press, Taylor & Francis Group, Boca Raton, FL, 2006.)

CRC_59645_Ch022.indd 535CRC_59645_Ch022.indd 535 3/20/2009 5:44:25 PM3/20/2009 5:44:25 PM

536 Lubricant Additives: Chemistry and Applications

which is equivalent to a spherical region ≈0.6 nm in diameter. At ambient pressure (100 kPa),

∆(pV)

vis

≈ 6.2 J/mol, so that near ambient conditions, ∆H

vis

≈ ∆E

vis

. Therefore, the viscosity is given by

⫽

⫺

ETS













()













exp

∆∆

vis vis

(22.6)

1×10

−2

1×10

−4

1×10

−2

1×10

−5

1×10

−1

1×10

−5

1×10

−1

1×10

ε′′ε′

ωa

(rad/s)

ωa

(rad/s)

Ztetraol 1000

Ztetraol 2000

Zdol 4000

(a)

(b)

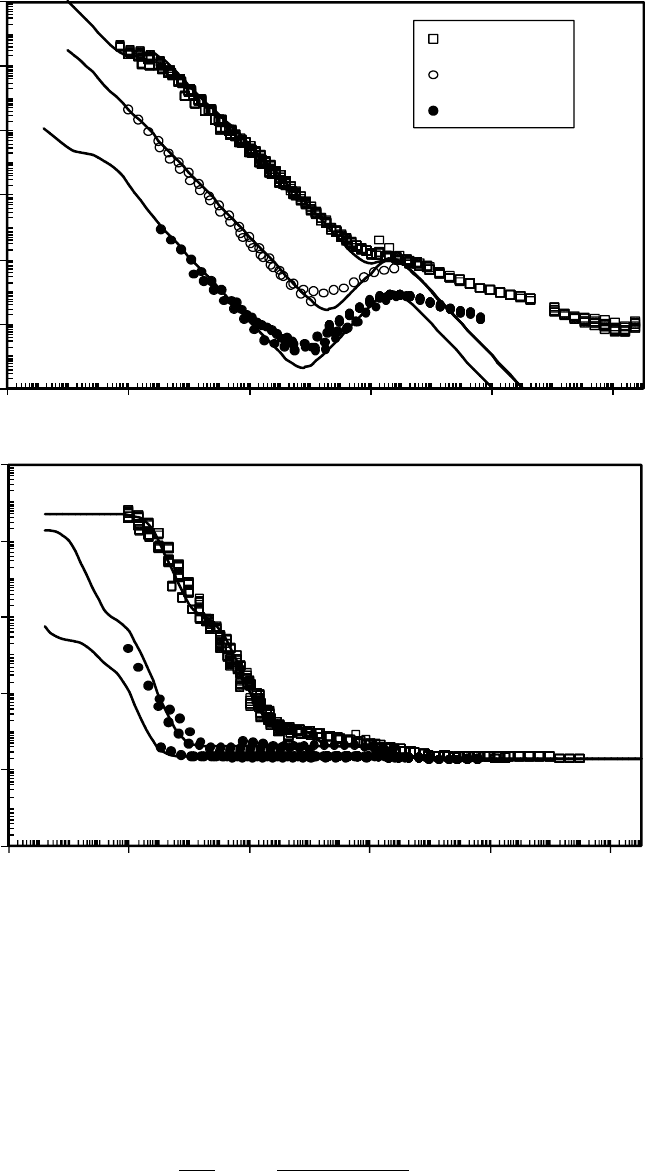
FIGURE 22.8 Dielectric loss factor (a) and relative permittivity (b) master curves for the Ztetraol 2000,

Ztetraol 1000, and Zdol 4000. The smooth curves are from the discrete relaxation time series  t to the

frequency–temperature shifted data. Reference temperature is T

= 50ºC. (Adapted from Rudnick, L.R. (ed.),

Synthetics, Mineral Oils, and Bio-Based Lubricants Chemistry and Technology, Chapter 38, CRC Press,

Taylor & Francis Group, Boca Raton, FL, 2006.)

CRC_59645_Ch022.indd 536CRC_59645_Ch022.indd 536 3/20/2009 5:44:25 PM3/20/2009 5:44:25 PM

Lubricants for the Disk Drive Industry 537

A regression  t to the bulk viscosity as a function of temperature [32] provided ∆E

vis

= 34.7 kJ/mol

and ∆S

vis

= 9.87 J/mol K. The  ow activation energy is close to that reported for bulk Zdol with a

molecular weight of 3100 Da in Refs 33 and 34. A positive value for the  ow activation entropy of

bulk Zdol means that the entropy of the  ow unit increases on going into the  ow- activated state.

Changes in the lubricant  ow activation energy and entropy near the solid surface cause changes

in the viscosity with decreasing  lm thickness. The  ow activation energy near a solid surface is

estimated from the thin  lm vaporization energy as follows. In an ideal gas, the chemical potential

µ (or partial molar Gibbs free energy) is given by

d ⫽ RT Pd ln

(22.7)

where P is the partial pressure of the lubricant in the vapor phase.

The chemical potential energy per unit volume in the lubricant  lm is µ/V

= Π. The ratio of the

 lm surface vapor pressure to the vapor pressure of the bulk lubricant, P

(h)/P

(∞), is derived by

integrating Equation 22.7

() ( ) ln

()

hRT

⫺⫽⬁

⬁













(22.8)

The reference state is taken to be the chemical potential and vapor pressure of the bulk lubri-

cant, u(∞) = 0, and P

(∞) is the vapor pressure of the bulk liquid.

In general, as the surface energy is de ned as the free energy per unit area, the total disjoining

pressure (Π) for these  uids can be derived from the experimental surface energy (contact angle)

data by

⫽⫺ ⫹

∂

()

(22.9)

TABLE 22.7

The Coefﬁ cients of the Debye Equation from the Dielectric Master Curves at

Reference Temperature T

= 50°C

Lubricant

Parameter Zdol 4000 Ztetraol 2000 Ztetraol 1000

ε′(0) 3.3 × 10

1.1 × 10

σ(S/m) 1 × 10

−11

4 × 10

−8

6 × 10

−7

s,1

3 × 10

1 × 10

(s) 500 50 8

s,2

3 × 10

1 × 10

(s) 50 5 0.8

s,3

30 100 100,000

(s) 5 0.5 0.06

s,4

24 5

(s) 1 × 10

−8

1 × 10

−8

1 × 10

−8

Note: The high frequency ε

∞

≈ 1.7 from the index of refraction.

Source: Adapted from Rudnick, L.R. (ed.), Synthetics, Mineral Oils, and Bio-Based Lubricants Chemistry and

Technology, Chapter 38, CRC Press, Taylor & Francis Group, Boca Raton, FL, 2006.

CRC_59645_Ch022.indd 537CRC_59645_Ch022.indd 537 3/20/2009 5:44:27 PM3/20/2009 5:44:27 PM

538 Lubricant Additives: Chemistry and Applications

Here γ

and γ

are the dispersive and polar components of the surface energy, respectively, and

h the  lm thickness.

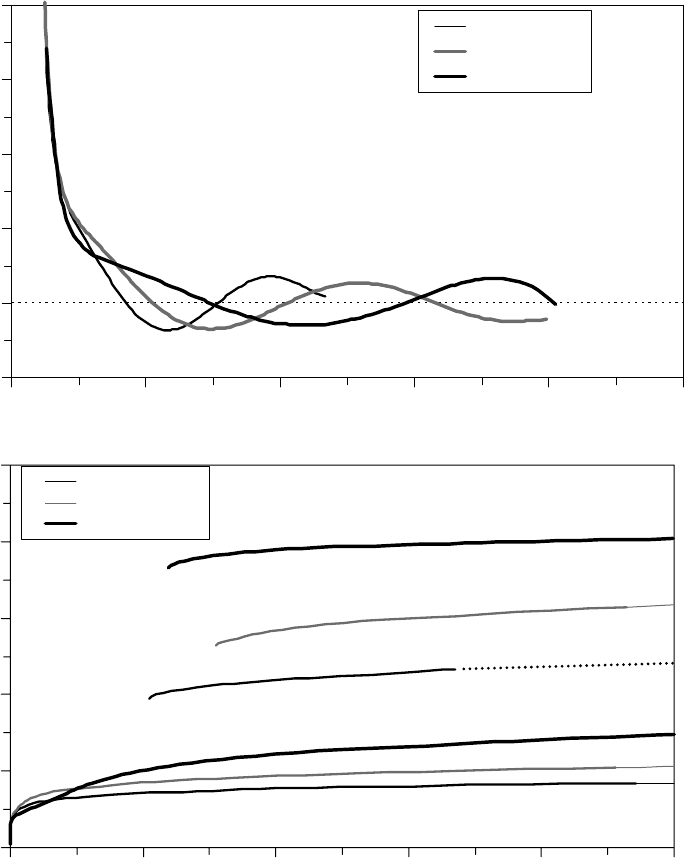
The regression  t to the surface energy data, shown as smooth curves in Figures 22.9a and 22.9b [1],

was numerically differentiated to obtain the disjoining pressure [35,36]. The total disjoining pres-

sure, including the individual contributions from the dispersive and polar components, is shown

in Figure 22.10a [1]. Notice that γ

decreases monotonically with h, which is consistent with

Equation 22.10. Below  lm thicknesses of ∼0.5 nm, Π at each molecular weight is dominated by

, which increases rapidly with decreasing  lm thickness and is largely independent of molecular

weight. The γ

, however, oscillates with  lm thickness and becomes larger in magnitude than γ

h increases. Oscillations in γ

provide an additional contribution to Π for PFPE Zdol that produces

alternating regions of stable and unstable  lm thickness [37]. The sum of the two contributions

0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5

Zdol thickness (nm)

Polar (mN/m)

1100 Da

1600 Da

3100 Da

(b)

0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5

Thickness (nm)

Dispersive (mN/m)

Zdol

(a)

FIGURE 22.9 The components of the surface energy measured on CHx-overcoated thin  lm magnetic

recording media with fractionated Zdol of narrow polydispersity index. (a) The dispersive component of the

surface energy for PFPE Z and Zdol. (b) The polar component of the surface energy for PFPE Zdol. (Adapted

from Rudnick, L.R. (ed.), Synthetics, Mineral Oils, and Bio-Based Lubricants Chemistry and Technology,

Chapter 38, CRC Press, Taylor & Francis Group, Boca Raton, FL, 2006.)

CRC_59645_Ch022.indd 538CRC_59645_Ch022.indd 538 3/20/2009 5:44:27 PM3/20/2009 5:44:27 PM

Lubricants for the Disk Drive Industry 539

gives rise to oscillations in the total disjoining pressure. It is remarkable that the disjoining pressure

from the surface energies as a function of  lm thickness, and Equation 22.8 relating the disjoin-

ing pressure to the degree of saturation predict the adsorption isotherms for low-molecular-weight

Zdols, according to P/P

= exp(−ΠV

/RT), which are shown in Figure 22.10b. There are two ther-

modynamically stable regions of  lm thickness for degrees of saturation corresponding to regions

where Π > 0 and ∂Π/∂h < 0. For thicknesses in between these regions, condensing Zdol molecules

will either reevaporate or form islands at the next higher stable  lm thickness.

0 0.2 0.4 0.6 0.8 1

P/P

Zdol thickness (nm)

1100 Da

1600 Da

3100 Da

(b)

−20

Zdol thickness (nm)

Π (Mpa)

1100 Da

1600 Da

3100 Da

(a)

01234

FIGURE 22.10 (a) The disjoining pressure from the fractionated Zdol surface energies in Figure 22.9a and

(b) the corresponding Zdol adsorption isotherms at 60°C. (Adapted from Rudnick, L.R. (ed.), Synthetics, Min-

eral Oils, and Bio-Based Lubricants Chemistry and Technology, Chapter 38, CRC Press, Taylor & Francis

Group, Boca Raton, FL, 2006.)

CRC_59645_Ch022.indd 539CRC_59645_Ch022.indd 539 3/20/2009 5:44:27 PM3/20/2009 5:44:27 PM

540 Lubricant Additives: Chemistry and Applications

For the purpose of explaining the viscosity increase of thin  lms, surface chemical potential is

approximated by the unretarded atom-slab dispersive interaction energy





⫽⫺

(22.10)

The dispersive interaction coef cient A is also referred to as the Hamaker constant and A = 10

−19

for Zdol.

As mentioned, the vaporization energy is the energy required to remove a molecule from the liquid

without leaving behind a hole, which is the energy needed to form a hole of the size of a molecule

in the liquid. The free volume needed for a  ow unit to transition into the  ow-activated state is less

than the size of the entire molecule. It is found that the ratio n ≡ ∆E

vap,∞

/∆E

vis,∞

> 3, where ∆E

vap,∞

and ∆E

vis,∞

are the vaporization and  ow activation energies of the bulk liquid, respectively. Thus,

the  ow activation energy near the surface is given approximately by





vis vis,

⫽⫺

⬁

(22.11)

For linear chains longer than 5 or 10 carbon atoms, n increases due to the onset of segmental  ow.

In practice, n is experimentally determined from the measured values of the vaporization and  ow

activation energy. For PFPE Zdol 4000, ∆E

vap,∞

= 166 kJ/mol, giving n ≈ 4.8. This is consistent

with segmental  ow.

To calculate the thin  lm viscosity with Equation 22.6, the  ow activation entropy near the

surface is also needed. Experimental  ow activation entropy is calculated from the spin-off data

[32] with Equations 22.6 and 22.11 as follows. The experimental η versus h is determined from

dh/dt during air shear-induced  ow on a rotating disk. Equation 22.6 is then solved for ∆S

vis

versus

h using Equation 22.11 for ∆E

vis

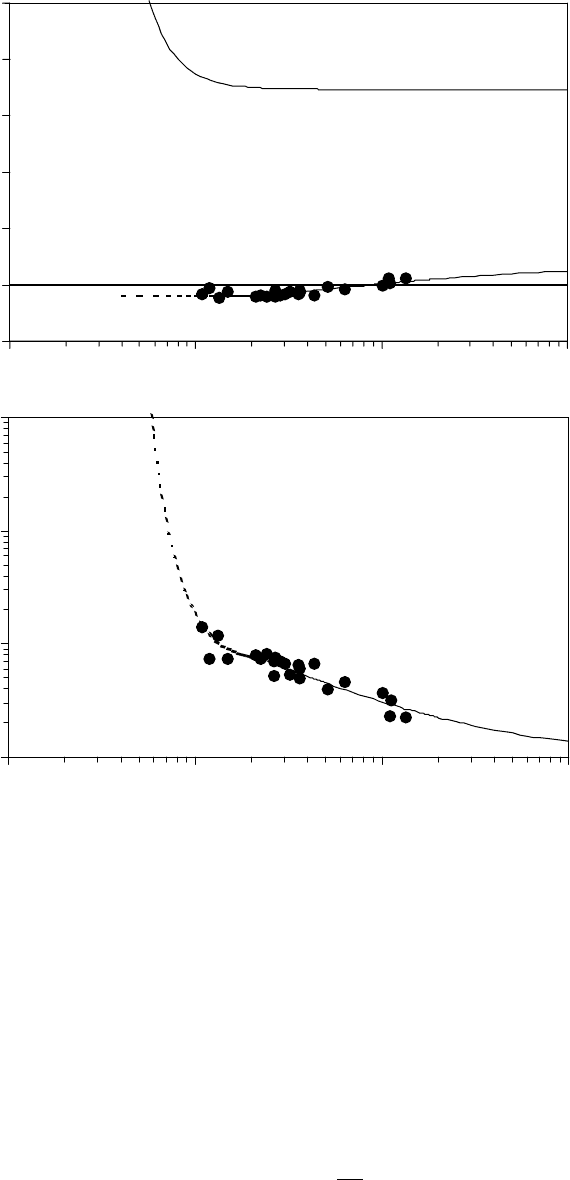
The  ow activation energy and entropy are shown in Figure 22.11a [1]. The  ow activation energy

suddenly increases below ∼0.8 nm due to the strong  lm thickness dependence of the dispersion force.

The retarding effect of this increase on  ow is compounded by the apparent effect of con nement on

restricting the degrees of freedom in the  ow transition state, as seen by the negative entropic contri-

bution in Figure 22.11a. Below 2.3 nm, T∆S

vis

≈ −1.9 kJ/mol, which corresponds to the critical con-

 gurational entropy change for  ow (−R ln 2 ≈ −5.76 J/mol °K). The combined effects give rise to the

observed increase in viscosity with  lm thickness shown in Figure 22.11b and enables extrapolation of

the viscosity to even thinner  lms where the spin-off is so slow that it takes years to measure.

The viscosity increases by a large amount with  lm thickness, which is much greater than the

increase with temperatures that might normally be encountered in the disk drive. The bulk viscosity

for several PFPE lubricants is shown in Figure 22.12 [1]. As the increase in viscosity with thickness

below ∼0.8 nm is much more than the increase with temperature between 0 and 60°C, the operating

temperature of disk drives should have no signi cant effect on lubricant spin-off from the disk by

air shear. That is, excluding air shear force due to the head suspension assembly and the air bearing

[38] and dispersion force between the lubricant and a low- ying slider [39].

22.2.1.4 Vapor Pressure

The vapor pressure of PFPE lubricants must be low to prevent evaporation from the disk. A method

to measure the vapor pressure was developed as follows. A model was derived to calculate the vapor

pressure from the measured Zdol molecular weight distribution and evaporation rate. Molecular

weight distributions were measured by GPC, as described in Karis et al. [28]. The vapor pressure

of discrete molecular masses was calculated from the evaporation rate measured by isothermal

thermogravimetric analysis (TGA) with a stagnant  lm diffusion model as described by Karis and

CRC_59645_Ch022.indd 540CRC_59645_Ch022.indd 540 3/20/2009 5:44:27 PM3/20/2009 5:44:27 PM

Lubricants for the Disk Drive Industry 541

Nagaraj [40]. Polymers such as Zdol differ from the low-molecular-weight synthetic hydrocarbon

oils in that polymers comprise various different molecular weights. Further considerations must be

taken into account in modeling the evaporation of polymers, as described later.

A numerical model was developed to simulate the evaporation of a polymer from an initial

molecular weight distribution measured by GPC. The evaporation simulation is written in terms of

mass  ux and the discrete form of the molecular weight distribution w

(t) as

wt wt t

ii i

() () ()

⫹

⫽⫺flux























(22.12)

−10

0.1 1.0 10.0 100.0

Zdol thickness (nm)

kJ/mol

(a)

100

1000

0.1 1.0 10.0 100.

Zdol thickness (nm)(b)

T∆S

vis

∆E

vis

η/η

∞

FIGURE 22.11 The vertical axis is de ned by the annotations on the curves in (a) Flow activation energy and

the entropic component of the  ow activation free energy and (b) dispersion-enhanced viscosity as a function

of  lm thickness. The  lled symbols are from the spin-off measurements, and the dashed region of the curve

was calculated with constant  ow activation entropy below 2.3 nm. Fractionated Zdol molecular weight 4500

Da, temperature 50°C. (Adapted from Rudnick, L.R. (ed.), Synthetics, Mineral Oils, and Bio-Based Lubricants

Chemistry and Technology, Chapter 38, CRC Press, Taylor & Francis Group, Boca Raton, FL, 2006.)

CRC_59645_Ch022.indd 541CRC_59645_Ch022.indd 541 3/20/2009 5:44:28 PM3/20/2009 5:44:28 PM

542 Lubricant Additives: Chemistry and Applications

where

A = surface area of the evaporating lubricant

= initial mass of lubricant

∆t = time step in the simulation

The mass  ux of the ith molecular weight fraction M

is given by stagnant  lm diffusion:

flux

P()⫽















(22.13)

Here D

is the vapor-phase diffusion coef cient and δ the diffusion length (calculated or measured

with a liquid of known vapor pressure).

The mass  ux divided by the mass density yields the rate of  lm thickness change. The solution

vapor pressure for the ith molecular fraction was approximated assuming an ideal solution according

to Raoult’s law P

= x

, where x

is the mole fraction of the ith molecular fraction.

The Hirschfelder approximation [41] is used for the vapor-phase diffusion coef cient

⫽⫻ ⫹

⫺

1 858 10

gas















(22.14)

where

gas

= molecular weight of the ambient atmosphere (air or nitrogen to suppress oxidation)

P = ambient pressure

= (σ

lube

+ σ

gas

)/2 = collision diameter

0.0

0.1

0.2

0.3

0.4

0.5

0 20 40 60 80 100

T (°C)

∞

(Pa s)

Z03

Zdol 4000

Ztetraol 2000

FIGURE 22.12 Bulk viscosity and  ow activation energy of several PFPE lubricants as a function of tem-

perature. (Adapted from Rudnick, L.R. (ed.), Synthetics, Mineral Oils, and Bio-Based Lubricants Chemistry

and Technology, Chapter 38, CRC Press, Taylor & Francis Group, Boca Raton, FL, 2006.)

CRC_59645_Ch022.indd 542CRC_59645_Ch022.indd 542 3/20/2009 5:44:28 PM3/20/2009 5:44:28 PM

Lubricants for the Disk Drive Industry 543

For nitrogen, σ

gas

= 0.315 nm. The vapor-phase molecular diameter of the ith molecular fraction

employed in estimating the binary mass diffusion coef cient is approximately given by σ

lube

2 × R

g,i

≈ 0.05 ×

√

___

, where the molecular weight M

is in daltons and the radius of gyration R

g,i

in nanometers. This expression was derived from the radius of gyration for Zdol measured in Freon

[42,43]. The molecular diameters from this approximation for a range of ideal monodisperse Zdol

molecular weights are listed in Table 22.8 [1].

By analogy to hydrocarbon oils, the collision integral Ω for collision between molecules in the

gas phase is a function of their binary Lennard–Jones interaction potential. The collision integral

between Zdol molecules and nitrogen molecules was taken to be the same as that for collision

between hydrocarbon molecules and nitrogen, Ω = 1.2.

The Clapeyron equation is employed to calculate the pure component vapor pressure:

1⫽⫺

⫺

exp exp exp



vap vap





















{}





















(22.15)

where the vaporization entropy ∆S

vap

= S

vap

– S

liq

is the difference between the entropy in the

vapor state and that in the liquid state. The Zdol liquid entropy is assumed to be independent

of molecular weight. It was determined along with the activation energy by comparison of the

simulated evaporation with isothermal TGA evaporation weight loss data. The liquid entropy for

Zdol, S

liq

= 107 J/mol K, is within the range obtained for the synthetic hydrocarbon oils. The vapor-

phase translational entropy for oils is approximated with the Sackur–Tetrode equation:

vap,trans

⫽⫹ ⫹

32 52

ln ln



() ( )





















()













(22.16)

TABLE 22.8

The Gas-Phase Molecular Diameter for Ideal Monodisperse Zdol Fractions

Calculated from the Radius of Gyration in Theta Solvent d = 0.05 √M

M (Da) d (nm)

Degree of

Polymerization

Contour

Length (nm)

Equilibrium

Thickness (nm)

500 1.12 3.54 2.71 0.66

750 1.37 6.29 4.06 0.74

1000 1.58 9.03 5.41 0.82

1350 1.84 12.88 7.29 0.93

1500 1.94 14.53 8.10 0.98

2000 2.24 20.02 10.79 1.14

3000 2.74 31.01 16.18 1.46

4000 3.16 42.00 21.56 1.79

4300 3.28 45.30 23.18 1.88

5400 3.67 57.38 29.10 2.24

Note: Also included are the degree of polymerization, the contour length measured along the chain from one

end to the other, and the equilibrium thickness. The equilibrium thickness is the maximum stable  lm

thickness, or dewettting thickness, determined from the  rst zero crossing of the disjoining pressure

with increasing  lm thickness.

Source: Adapted from Rudnick, L.R. (ed.), Synthetics, Mineral Oils, and Bio-Based Lubricants Chemistry

and Technology, Chapter 38, CRC Press, Taylor & Francis Group, Boca Raton, FL, 2006.

CRC_59645_Ch022.indd 543CRC_59645_Ch022.indd 543 3/20/2009 5:44:28 PM3/20/2009 5:44:28 PM