Rudnick L. Lubricant Additives: Chemistry and Applications (Присадки, добавки к смазкам)
Подождите немного. Документ загружается.


364 Lubricant Additives: Chemistry and Applications
Also in Equations 13.3 and 13.4, α and β are numerical parameters, whose values are estimated by
tting, and
⫽⫽⫽⫹⫹ ⫹mm() ( / ) ( / )
22
2
3
11
2
11⫺
(13.5)
The rst and second terms in identical expression 13.4 for stress σ
0
describe, respectively, the
contributions of weight and surface tension of the liquid column in the meniscus area 2. The bottom
stress σ
0
, being due to Equation 13.4 a function only of R (or r
0
), has a minimum at R = R
c
(or r
0c
).
The minimum value of initial stress σ
0min
and corresponding values of R
c
(or r
0c
) and q
c
are given by
01
12
2
12
0
2
12
3
min
⫽⫽⫽ ⫽cg R
c
g
r
c
g
q
c
g
cc c
()
32
122 3
2
2
8
22
cmc
m
c
m
c
c
⫽⫽⫽⫽
(13.6)
where numerical parameters c
1
, c
2
, cˆ
2
, and c
3
are calculated using Equation 13.5. The values of R
c
(or r
0c
) and q
c
have a physical sense of critical parameters, below which the jet structure does not
exist [7,9]. Remarkably, these values depend only on the equilibrium physical parameters of the
uid, its density ρ and surface tension γ, being independent of the withdrawal conditions and visco-
elastic constants of liquid.
To analyze the jet behavior in region 1, we rst mention unusual ow phenomenon in the suck-
ing tube (capillary), recorded in experiments and shown by a photograph in Figure 13.4.
Here, the jet entered the tube with considerably less diameter than the inner capillary diameter
and, at higher vacuum, seemingly continued its extension up to the upper capillary end. It means
that instead of visible jet length l(t) introduced earlier, the total jet length L(t) at higher vacuum
should be considered as the real dynamic variable, where
L(t) = l(t) + l
T
(13.7)
and l
T
is the sucking tube length.
In case of withdrawal of dilute polymer solutions, an additional effect of strain-induced exuda-
tion of solvent should also be taken into account. Although the kinetics of this process is unknown,
the ow of a thin lm of solvent covering the gelled jet, swollen in the solvent, is guessed to be
much the same as in the case of thin lm withdrawn from a vessel by a vertical wall moving
upward, that is, controlled by the vertical drag speed, viscosity, gravity, and surface tension [10].
To take into account solvent exudation, we introduce the two-phase model of jet sketched in the
box of Figure 13.3, where the actual radius r of jet is represented as the sum of actual radius r
g
of
the gelled jet and the precipitated lm thickness h, that is, r = r
g
+ h. At any radius r, we roughly
treat the core of the swollen jet with radius r
g
as an elastic solid with large deformations, whereas the
peripheral thin lm of solvent with thickness h as a viscous liquid. We neglect the contribution of
the solvent lm in axial stretching stress. Yet we consider in this two-phase model the local surface
tension effect as acting on the total radius r.
We then roughly hypothesize that the lm thickness h depends only on time. Using also the
scaling argument, we assume that h ≈ ξr
0
(t), where ξ = ξ(q
c
/q) is a positive increasing function,
and r
0
(t) is the maximum radius of the jet at time t (see Figure 13.3). Thus, this two-phase approach
yields the kinematical relation
rr ht r
q
qt
rt
gg
⫽⫹ ⫽⫹()
()
()
0
0
(13.8)
CRC_59645_Ch013.indd 364CRC_59645_Ch013.indd 364 10/31/2008 2:24:33 PM10/31/2008 2:24:33 PM

Tackifi ers and Antimisting Additives 365
Neglecting a possible effect of the solvent lm in the region 2, the dependence r
0
(t) will be cal-
culated at the end of this section, using the kinetics of jet withdrawal and analyzing effects in the
region 2. The function ξ(q
c
/q(t)) will be proposed in Section 13.5.
We now use the aforementioned assumption that, in region 1, the core of gelled jet behaves as
a weakly cross-linked purely elastic solid with a very low elastic modulus µ and very large elastic
strain λ (>>1). We employ in region 1 slightly inhomogeneous quasi-one-dimensional common
approach, almost the same as in the homogeneous extension (e.g., see Refs 7 and 9). Then using
Equation 13.8 yields
⫽⫽
0
0
2
0
0
0
2
1
r
r
r
rr
g
g
()
()
⫺
⫺
(13.9)
艐
nr
n
n
⫺⬎()1 (13.10)
where
λ and σ = stretch ratio and stress, respectively
n = numerical parameter characterizing a speci c elastic potential [9]
λ
0
= extensional stretch ratio attributed to the liquid–solid transition in region 2
FIGURE 13.4 Photograph of two-phase motion of jet in capillary.
CRC_59645_Ch013.indd 365CRC_59645_Ch013.indd 365 10/31/2008 2:24:33 PM10/31/2008 2:24:33 PM
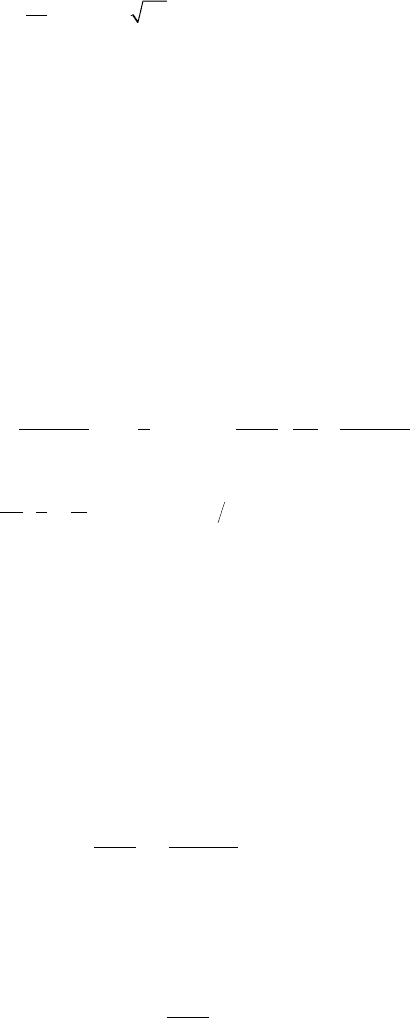
366 Lubricant Additives: Chemistry and Applications
The noninertial momentum and mass balance equations, averaged over the jet cross-section, can be
written in the form similar to those used in Refs 7 and 9:
d
dz
SSgSSrSr
ggg
⫺ 2
22
()
(
)
⫽⫽⫽,
(13.11)
uS u S u S q t S S S
gg f f f g
⫽⫹⫽() ⫽⫺
(
)
(13.12)
where
S, S
g
, and S
f
= total, occupied by gel, and occupied by solvent lm cross-sectional areas,
respectively
r = actual radius of jet
u, u
g
, and u
f
= total, gel, and solvent lm vertical velocities, respectively
Note that if u
g
≈ u, then u
f
≈ u either. It means that the solvent lm is drawn upward with the same
speed as the gel.
Substituting Equations 13.9 and 13.10 in Equation 13.11 yields the following solution of the
stress–strain problem (Equations 13.4 through 13.6) described by the two-phase model:
σ=
()
⋅
()
G
r
rr r
zR
n
n
G
g
r
rr
n
0
0
0
2
0
0
0
1
1
1⫺
⫺
⫺⫺
⫺
⫺
⫺
⫽
22
0
00 0
1
11
n
gr r
Gr
⫺
⫺⫺
()
⫽⫹
(13.13)
Equation 13.13 in the limit ξ → 0 has the same form as in Refs 7 and 9. Parameters r
0
, S
0
, σ
0
, and
G
0
in Equation 13.8 are slow functions of time. They represent the boundary values of respective
variables at the level z = R. These boundary values should be determined by matching the behavior
of liquid in regions 1 and 2. Also the function ξ(q
c
/q
0
) is a slow function of time. As soon as these
values are found, the jet pro le and the stress distribution along the jet in the region (R < z < L(t))
are determined for any time instant from Equation 13.13.
We now consider the long jets with such large values of z that the surface tension effects on the
stress are negligible as compared with the gravity. For these values of z, the solution of Equation 13.13
of the withdrawal problem has the asymptotic form found in Refs 7 and 9:
艐 g
n
n
z
mc
c
Rcmn n
⫺
⫺
⫺
1
1
1⫹⫽
()
(()/)
(13.14)
where the numerical parameter c is again expressed through α and β using Equation 13.12. When
the rst term in the bracket in Equation 13.14 dominates, the following simpli ed expression will
be used:
艐
gzn
n
zR
⫺
⬎⬎
1
()
(13.15)
Equations 13.9 through 13.15 have been obtained in Ref. 9 for the stationary withdrawal prob-
lem in the limit ξ → 0 using the noninertial approach. In Ref. 9, the characteristic sizes R and r
0
of the meniscus as well as the ow rate q have certain constant values. In the nonsteady case of
CRC_59645_Ch013.indd 366CRC_59645_Ch013.indd 366 10/31/2008 2:24:33 PM10/31/2008 2:24:33 PM

Tackifi ers and Antimisting Additives 367
jet withdrawal under study, these formulae are still valid because of a slow noninertial approach,
although the basic kinematical variables of the process, the length of withdrawn jet L(t), and the
ow rate q are now some functions of time t. To determine these functions L(t) and q(t), we will use
two additional physical conditions.
The rst, kinematical condition evident from Figures 13.1 and 13.3 is
qt A
dL
dt
()⫽ ⋅
(13.16)
where A = πr
j
2
is the cross-sectional area of the measuring cylinder (jar). Equation 13.16 shows
that the change in length of the withdrawn jet is caused by the decrease of the liquid level in
the jar.
The second, dynamic condition describes the dependence of ow rate on the pressure drop for
the liquid ow in the sucking capillary. If there were a back gel– uid transition in the sucking capil-
lary, this dependence must be described by the well-known linear Poiseuille formula. However, this
back gel– uid transition was never observed in the sucking capillary. Instead, a very complicated
two-phase ow shown in Figure 13.4 occurs there. It seems that at the highest vacuum, the jet con-
tinues to extend in the sucking capillary up to its very end. After that, the jet breaks down of the
two-phase liquid–air mixture in the adjacent tube. At lower values of vacuum, this breaking pro-
cess happens in the sucking capillary. Because of the relative slowness of the withdrawal process,
this typically viscous, complicated ow could still be described by a linear hydraulic-type relation
between the pressure drop and the ow rate:
qk k p p
L
艐 (
vvav
⫺⫺) constant⫽⫽ (13.17)
where
σ
v
= pulling stress due to vacuum
p
v
and p
a
= absolute vacuum and atmospheric pressures, respectively
σ
L
= acting elastic stress in the jet at the level z = L(t)
The constant k of dimensionality (cm
3
/Pa s) describes the hydraulic resistance of jet at the end of
sucking capillary. It should be evaluated by comparing theory with experimental data.
Determining σ
L
from asymptotic equation 13.15 at z = L(t) and substituting it along with Equa-
tion 13.17 in Equation 13.16 yields the kinetic equation describing the time evolution of L(t):
dL
dt
sL sL
u
⫹⫽
(13.18)
where s is a parameter of dimensionality of one per second and L
u
the ultimate length of the whole
jet achievable with a given vacuum; these parameters are described as
s
n
n
gk
A
L
n
n
u
⫽⫽
⫺
⫺
1
1
⋅⋅
v
g
(13.19)
Beginning with a time t
*
where the asymptotic equation 13.15 is valid, solution of Equation 13.18
is presented as
Lt L st t t t
u
( ) { exp[ ( )]} ( )
**
⫽ ⋅ 1⫺⫺⫺ ⱖ
(13.20)
CRC_59645_Ch013.indd 367CRC_59645_Ch013.indd 367 10/31/2008 2:24:34 PM10/31/2008 2:24:34 PM
368 Lubricant Additives: Chemistry and Applications
Finally, Equations 13.16 and 13.20 yield the asymptotic expression for the ow rate
qsL stt t t
u
⫽ ⋅⋅exp[ ( )] ( )
**
⫺⫺ ⱖ
(13.21)
Equations 13.19 and 13.21 will be used in Section 13.5 for the evaluation of parameters s and
elastic constant of gel n. We should remember once again that these relations are reliable only
after a certain time t
*
elapsed from the beginning of the withdrawal process when Equation 13.15
is valid.
To describe the whole process from its very beginning, one should employ numerical calcula-
tions using Equations 13.3 through 13.7, where z = L(t), S = S(l(t)) ≡ S
l
(t). Although these cal-
culations can be performed relatively easily, the problem is that the beginning of withdrawal is
accompanied by a poorly understood two-phase motion of jet in capillary.
13.5 EXPERIMENTAL RESULTS WITH A 0.025% PIB
SOLUTION: COMPARISON WITH THE THEORY
We rst attract attention to the jet photographs presented in Figures 13.2a and 13.2b made with 5.3
magni cation. Some horizontal ripples on the jet are clearly seen, which might be explained by
secondary instability of solvent lm exuded out of solvent. This instability well known for the liquid
lms owing down on inclined surfaces [11] indirectly con rms the very fact of exudation of the
solvent from the withdrawn jet.
With increasing time of withdrawing, the diameter of jet dramatically decreases. The amount
of liquid sucked from calibrated cylinder was measured every 5 s. Using these data, the time depen-
dences of ow rate q (cm
3
/s) were determined for different applied values of vacuum (Figure 13.5).
At the beginning of withdrawing, ow rate q substantially increases in time and reaches a
maximum at ∼25 s from the beginning of withdrawing. The higher the vacuum the higher is the q
maximum and earlier its achieving. The possible explanation of the effect is as follows. The initial,
just formed short jet is under the action of surface tension and extension from sucking capillary. The
0
10
20
30
40
50
60
70
0 50 100 150 200 250
Time (s)
q (cm
3
/s)×10
−2
510
580
630
FIGURE 13.5 Time dependences of ow rate for different vacuum values (shown in the inset) for 0.025%
PIB solution in lubricant oil.
CRC_59645_Ch013.indd 368CRC_59645_Ch013.indd 368 10/31/2008 2:24:34 PM10/31/2008 2:24:34 PM
Tackifi ers and Antimisting Additives 369
action of surface tension squeezes the jet causing the increase in the ow rate. With increasing jet’s
length, the gravity force comes into play and soon overcomes the surface tension effect, causing the
decrease in ow rate.
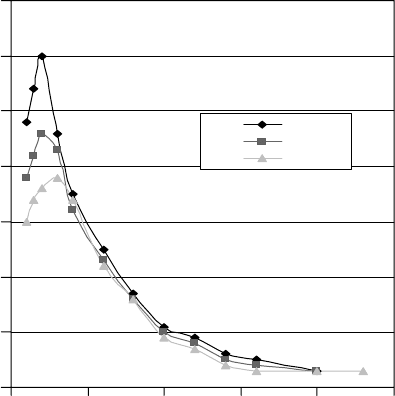
Figure 13.6 demonstrates that the ow rate is proportional to the speed of change in the length
of jet dl/dt (=dL/dt). This is the direct con rmation of evident kinematical relation 13.16 on the
example of the highest used vacuum.
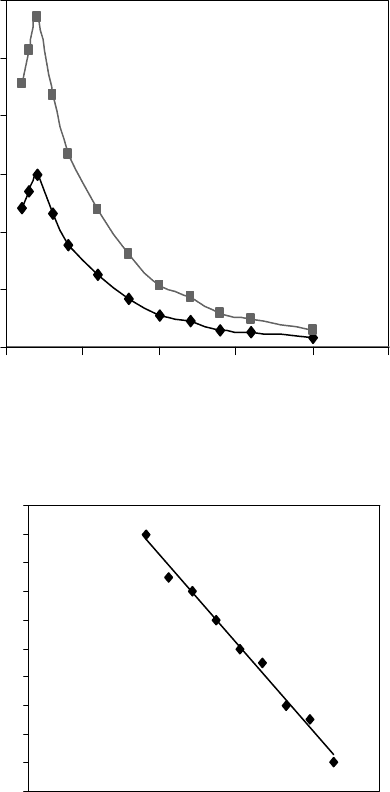
After passing through the maximum, the ow rate exponentially decreases. This effect, pre-
dicted by Equation 13.21 is illustrated in Figure 13.7, where the time dependence of ln q is presented
by a straight line with the slope equal to about –0.02 (s
–1
). As seen from Figure 13.7, the decrease in
applied (constant) value of vacuum also causes the decrease in ow rate, but after passing through
the maxima, the differences between curves with different values of vacuum are negligible. Thus,
0
20
40
60
80
100
120
0 50 100 150 200 250
Time (s)
(1) q (cm
3
/s) ×10
−2
,
(2) ᐉ (mm/s) ×10
−2
FIGURE 13.6 Comparison of time dependences of withdrawal rate i(t) (curve 1) and ow rate (curve 2) with
vacuum value σ
v
= 32 kPa for 0.025% PIB solution in lubricant oil.
−3.00
−2.80
−2.60
−2.40
−2.20
−2.00
−1.80
−1.60
−1.40
−1.20
−1.00
0 50 100 150
ln q (cm
3
/s)
Time
(
s
)
FIGURE 13.7 The decreasing branches time dependences of ow rate in Figure 13.5, represented in
semilogarithmic coordinates.
CRC_59645_Ch013.indd 369CRC_59645_Ch013.indd 369 10/31/2008 2:24:34 PM10/31/2008 2:24:34 PM
370 Lubricant Additives: Chemistry and Applications
the data presented in Figure 13.7 illustrate the changes of average ow rate with time for three dif-
ferent values of vacuum.
Another important fact found in this chapter is that independent of the vacuum values, all
jets break at a ow rate of ∼0.03 cm
3
/s. The very existence of a lower critical value of ow rate is
predicted by the fourth formula in Equation 13.6. This fact will also be utilized in the following
modeling.
Using the data presented in Figure 13.5, we choose on the decreasing branches q(t) several ow
rates, q
1
= 0.35, q
2
= 0.25, q
3
= 0.20, and q
4
= 0.14 cm
3
/s, corresponding to various time instances
t
k
. Making photographs at these t
k
, we measured the jet pro les corresponding to the ow rates q
k
related to these instances t
k
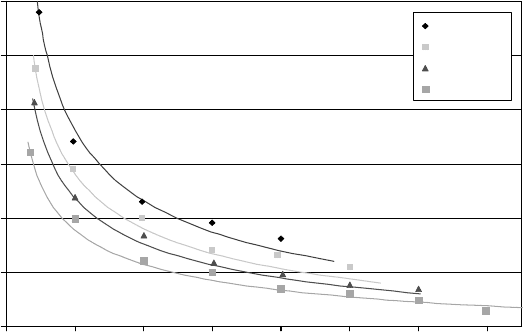
. In this region of ow rates, the measured jet pro les were well repro-
duced. Figure 13.8 presents these jet pro les as decreasing dependences of the jet radius r versus
distance z from the liquid surface, up to the maximal visible jet length at those time instances t
k
.
To describe the jet pro les shown in Figure 13.8, we had to nd along with the function ξ(q
c
/q(t))
describing the thickness of exuded solvent in Equation 13.13, three tting parameters, numeri-
cal parameters ν related to the meniscus (Equations 13.3 through 13.5), numerical parameter n
describing the gel elastic potential (Equation 13.10), and parameter κ describing the stress- ow rate
hydraulic relation (Equation 13.17).
We rst evaluate the parameters of meniscus. Starting with the highest value of ow rate
q
1
= 0.35 cm
3
/s, and using the aforementioned awkward procedure of meniscus approximation,
we found the value r
01
≈ 0.49 mm corresponding to the maximum ow rate q
1
. All other values
r
0k
corresponding to different values of q
k
have been calculated using the scaling Equation 13.3 as
r
0k
= r
01
(q
k
/q
1
)
1/3
. As seen from Figure 13.8, the calculated data presented in Table 13.1 match
well with the experimental values. Then, using the fact that the lower critical value of ow rate
q
0c
≈ 0.03 cm
3
/s, we calculated the lower critical value of r
0c
as r
0c
= r
01
(q
1
/q
c
)
1/3
= 0.216 mm.
Using this value, we employ Equation 13.6 for r
0c
and Equation 13.5 for function m(ν) to yield the
equation νm(ν) ≡ ν(0.0959ν
2
+ 0.42ν + 1) ≈ 137. Solution of this equation is ν ≈ 9.7 and m ≈ 14,
respectively. Using these data, we calculated the values of large meniscus radiuses R = νr
0
, menis-
cus stress σ
0
due to Equation 13.4, and the values of parameter G
0
in Equation 13.13. These vari-
ables for the aforementioned four pro les are presented in Table 13.1.
r(z)
0.2
0.25
0.3
0.35
0.4
0.45
0.5
0 10203040506070
z (mm)
r (mm)
q = 0.35
q = 0.25
q = 0.2
q = 0.14
−
−
−
−
FIGURE 13.8 Jet pro les for several values of ow rate (shown in the box) for 0.025% PIB solution in lubri-
cant oil established by photographing. Symbols—experimental data, solid lines—model calculations.
CRC_59645_Ch013.indd 370CRC_59645_Ch013.indd 370 10/31/2008 2:24:35 PM10/31/2008 2:24:35 PM
Tackifi ers and Antimisting Additives 371
Elastic potential for the highly swollen elastic gel is unknown. It is characterized by the param-
eter n, which is determined by a tting procedure as follows. Consider Equation 13.19 for the total
ultimate length L
u
of the jet. Using the values of vacuum pressure reported in Section 13.2, we found
that the corresponding values of pulling vacuum stress σ
v
are 32, 22.7, and 16 kPa, respectively.
Consider the maximal value σ
v
= 32 kPa. Experimental results show that for this value of vacuum,
the visible maximal length of withdrawn jet l
u
≈ 10 cm, so that the ultimate total jet value L
u
≈ 22 cm.
Thus from the Equation 13.19 for L
u
, we found n ≈ 1.062.
Being unaware of strain-induced exudation kinetics of solvent out of gel, we simply parameter-
ize the function ξ(q
c
/q(t)) by a power relation ξ = (q
c
/q)
a
. Fitting the jet pro les in Figure 13.8 with
Equation 13.13, we quickly found that a ≈ 1/2, that is, the thickness of the solvent lm exuded out
of gel under gel stretching is described as
hrr
q
q
c
⫽⫽ ⋅
00
(13.22)
Simplicity of this result could indicate a fundamental physics of strain-induced solvent exudation
out of the cross-linked swollen gel. Revealing this physics is, however, outside the scope of this
chapter.
Using the aforementioned values of meniscus parameters and parameter n along with
Equation 13.22, we calculated jet pro les according to the Equation 13.13. Figure 13.8 shows a
good agreement between the calculations (solid lines) and experimental data (points).
We now consider the modeling of kinetics of long jet withdrawal, asymptotically described
by Equations 13.16 through 13.20. Figure 13.6, discussed earlier, veri es the kinematical Equa-
tion 13.16 on the example of higher pulling vacuum stress. Finally, the parameter k introduced
in the hydraulic Equation 13.17 is evaluated using Equation 13.18 and value s = 0.02 s
−1
as k ≈
2.71 × 10
−5
cm
3
/(Pa⋅s). Data of Figure 13.5 by using Equation 13.20 and obtained values for s
and L
u
allow determine the time t
*
≈ 32 s starting from which ow rate decays exponentially
with time.
We now point out that the relaxation time θ could not be directly determined from the afore-
mentioned experimental data. Using these data, we can calculate only the value
13 2 13
695 10
/
.(s)艐 ⫻
⫺
(13.23)
Direct measurement of relaxation time θ in our very dilute polymer solutions is very dif cult. One
possible way is to evaluate its value using the formula, roughly describing the longest relaxation
time in the Rouse model (e.g., see Ref. 4, p. 222)
R
S
M
NkT
⫽
[]
0
AB
(13.24)
TABLE 13.1
The Values of Meniscus Variables in the Experimental Profi les (Figure 13.8)
q (cm
3
/s) (q
c
) 0.03 0.14 0.20 0.25 0.35
r
0
(mm) 0.216 0.361 0.407 0.438 0.490
R (mm) 2.10 3.50 3.94 4.25 4.75
σ
0
× 10
−2
(Pa) 4.97 5.63 5.98 6.25 6.71
G
0
× 10
–2
(Pa) 6.22 6.38 6.65 6.87 7.26
CRC_59645_Ch013.indd 371CRC_59645_Ch013.indd 371 10/31/2008 2:24:36 PM10/31/2008 2:24:36 PM

372 Lubricant Additives: Chemistry and Applications
where
[η]
0
= intrinsic viscosity whose value is ∼4 is known for the lubricant liquids [12]
η
s
= solvent viscosity
M = polymer molecular weight
N
A
= Avogadro number
k
B
= Boltzmann constant
T = absolute temperature
At the room temperature, using these values of constants for 0.025% PIB solution in lubricant oil
yields the value θ
R
≈ 4.54 × 10
−4
s.
Another way of evaluating the relaxation time is hypothesizing that near the sol–gel transition,
the polymer concentration in the jet highly increases causing cooperative relaxation effects. Then,
we can speculate that the transition happens under the condition We
c
= constant, with universal
value of We
c
. Roughly estimating the critical value ε
c
of strain rate in the transition as ε =q/(πr
0
2
R)
results in the relation
We
q
rR
ccc
c
⫽⫽
⋅
艐
0
23
1
(13.25)
Using now the assumption of universality of We
c
, we can use the data of Refs 8 and 9, where in
case of 0.5% PEO water solution, ν
PEO
= 2.6 and β
PEO
= 0.334, and calculate We
c
≈ 3.3. Then,
the value of β in our case where ν = 9.7 is calculated as β = (πνWe
c
)
−1/3
≈ 0.215. Substituting this
value of β in Equation 13.22 yields: θ
c
≈ 3.38 × 10
−2
s. Remarkably, the value of θ
c
is almost two
orders of magnitude higher than θ
R
. In our opinion, the value θ
c
and related value of parameter β
seems preferable. The values of basic constants in Equation 13.21 obtained using tting procedure
are presented in Table 13.2.
13.6 USING OPEN SIPHON METHOD FOR THE EVALUATION
OF TACKINESS OF LUBRICATING FLUIDS
As mentioned earlier, the ultimate jet length (or tackiness) strongly depends on the viscosity of oil,
molecular weight of dissolved polymer, and its concentration in solution. Figure 13.9 shows the
dependence of jet length l on the concentration of PIB with M
η
≈ 2,000,000 in two paraf nic oils
with respective viscosities 0.068 Pa s and 0.022 Pa s at 40ºC.
One can see that the dependences of tackiness on polymer concentration in different oils are
linear. These dependences are in fact linear for any molecular weight in different oils. It is clear
from Figure 13.9 that decreasing oil viscosity is accompanied by a large decrease in tackiness. For
example, at the concentration 0.025% of PIB, the jet length in oil with viscosity 0.068 Pa s is equal
to 100 mm, whereas in oil with viscosity 0.022 Pa s, it is equal to 20 mm, that is, ve times less than
that in the rst case.
Data presented in Figure 13.10 demonstrate what concentration of PIB with different molecular
weights in oil with viscosity 0.068 Pa s should be used to reach the jet length of 100 mm. It is seen
that, by simply increasing the molecular weight, it is possible to substantially increase the tackiness.
TABLE 13.2
The Values of Basic Constants in Equation 13.21 Obtained Using Fitting
Procedure
βνα = βν m(ν) nk (cm
3
/Pa s) θ (s)
0.215 9.7 2.08 14 1062 2.71 × 10
−5
3.38 × 10
−2
CRC_59645_Ch013.indd 372CRC_59645_Ch013.indd 372 10/31/2008 2:24:36 PM10/31/2008 2:24:36 PM

Tackifi ers and Antimisting Additives 373
Increasing molecular weight causes, however, a decrease in both thermal/oxidative stability and
shear stability.
Combining the data presented in Figures 13.9 and 13.10, it is possible to evaluate the jet length or
tackiness for PIB solutions with different molecular weights at different polymer concentrations.
Unlike PIBs commonly used as tacki ers, the ethylene/propylene copolymers usually do
not display tackiness. Nevertheless we obtained some unusual data for the blend of PIB with
M
η
≈ 2,000,000 with very small additive of ethylene/propylene copolymer. Figure 13.11 demon-
strates that adding 0.01% of the copolymer to the PIB solution increases the jet length by ∼30%.
It should also be mentioned that addition of 0.01% of copolymer to the solution of 0.025% of PIB
practically does not change viscosity of the solution. As seen from Figure 13.11, at higher concentra-
tion of the copolymer in PIB solutions, the tackiness decreases.
This effect might be explained as follows. Solutions that have 0.01% of copolymer could be
considered as very dilute, with macromolecules well separated. During ow-induced orientation
of long exible PIB chains, much shorter and more rigid molecules of copolymer are involved in
the process of orientation and support-oriented PIB macromolecules, causing increase in tackiness.
With increase in concentration of copolymer, macromolecules form ensembles, which could not be
0
10
20
30
40
50
60
70
80
90
100
0.0000 0.0100 0.0200 0.0300 0.0400 0.0500 0.0600 0.0700 0.080
0
C (%)
Z (mm)
FIGURE 13.9 Ultimate jet length l versus the concentration of PIB with M
η
≈ 2,100,000 in two paraf n oils
with respective viscosities 0.068 and 0.022 Pa s at 40ºC.
0
2
4
6
8
10
12
14
MW (×10
6
)
C% × 10
−2
102345
FIGURE 13.10 Concentration C% of PIB in oil with viscosity 0.068 Pa s corresponding to the jet length
l = 100 mm versus viscosity average molecular weight M
η
of polymer.
CRC_59645_Ch013.indd 373CRC_59645_Ch013.indd 373 10/31/2008 2:24:36 PM10/31/2008 2:24:36 PM
