Руденко В.М. Математична статистика
Подождите немного. Документ загружается.


31
Ⱥɬɪɢɛɭɬɢɜɧɿ ɪɨɡɩɨɞɿɥɢ
Ⱥɬɪɢɛɭɬɢɜɧɿ ɪɨɡɩɨɞɿɥɢ ɜɢɤɨɪɢɫɬɨɜɭɸɬɶɫɹ ɭ ɪɚɡɿ
ɧɨɦɿɧɚɥɶɧɢɯ (ɤɚɬɟɝɨɪɿɚ-
ɥɶɧɢɯ) ɬɢɩɿɜ ɜɢɦɿɪɸɜɚɧɶ ɜɥɚɫɬɢɜɨɫɬɟɣ ɞɨɫɥɿɞɠɭɜɚɧɢɯ ɨɛ’ɽɤɬɿɜ.
ɉɪɢɤɥɚɞ 2.5. Ɋɨɡɪɚɯɭɜɚɬɢ ɪɨɡɩɨɞɿɥɢ ɨɫɿɛ ɡɚ ɪɟɡɭɥɶɬɚɬɚɦɢ ɬɟɫɬɭɜɚɧɧɹ ɜɥɚ-
ɫɬɢɜɨɫɬɟɣ ɜɢɳɨʀ ɧɟɪɜɨɜɨʀ ɞɿɹɥɶɧɨɫɬɿ (ȼɇȾ) 16 ɨɫɿɛ (ɪɢɫ. 2.18). ɉɨɛɭɞɭɜɚɬɢ
ɜɿɞɩɨɜɿɞɧɿ ɝɪɚɮɿɤɢ ɪɨɡɩɨɞɿɥɭ.
ɉɨɫɥɿɞɨɜɧɿɫɬɶ ɪɿɲɟɧɧɹ:
x ɜɢɛɿɪɤɨɜɿ ɟɦɩɿɪɢɱɧɿ ɞɚɧɿ ɜɧɟɫɬɢ ɭ ɫɬɨɜɩɱɢɤɢ Ⱥ:D;
x ɡɝɿɞɧɨ ɡ ɬɢɩɨɦ ȼɇȾ ɤɨɠɧɿɣ ɨɫɨɛɿ ɧɚɞɚɬɢ ɜɿɞɩɨɜɿɞɧɢɣ ɚɬɪɢɛɭɬ x
i
, ɧɚ-
ɩɪɢɤɥɚɞ, «ɯɨɥɟɪɢɤ» – 1; «ɫɚɧɝɜɿɧɿɤ» – 2 ɿ ɬ.ɞ. (ɫɬɨɜɩɱɢɤɢ C:D ɿ E:F);
x ɞɥɹ ɪɨɡɪɚɯɭɧɤɭ ɚɛɫɨɥɸɬɧɢɯ ɱɚɫɬɨɬ m
i
ɭ ɤɨɦɿɪɤɭ G3 ɜɧɟɫɬɢ ɜɢɪɚɡ
=ɋɑȬɌȿɋɅɂ($D$3:$D$18;F3). Ⱥɧɚɥɨɝɿɱɧɿ ɜɢɪɚɡɢ ɜɧɟɫɬɢ ɜ ɤɨɦɿɪɤɢ G4:G6;
x ɞɥɹ ɪɨɡɪɚɯɭɧɤɭ ɡɚɝɚɥɶɧɨʀ ɤɿɥɶɤɨɫɬɿ ɨɛ’ɽɤɬɿɜ n ɭ ɤɨɦɿɪɤɭ G7 ɜɧɟɫɬɢ ɜɢ-
ɪɚɡ =ɋɍɆɆ(G3:G6);
x ɞɥɹ ɪɨɡɪɚɯɭɧɤɭ ɜɿɞɧɨɫɧɢɯ ɱɚɫɬɨɬ m
i
/n ɭ ɤɨɦɿɪɤɭ H3 ɜɧɟɫɬɢ ɜɢɪɚɡ:
=G3/$G$7, ɚɧɚɥɨɝɿɱɧɿ ɜɢɪɚɡɢ ɜɧɟɫɬɢ ɭ ɤɨɦɿɪɤɢ H4:H6. ɍ ɤɨɦɿɪɤɭ H7 ɜɧɟɫɬɢ
ɜɢɪɚɡ =ɋɍɆɆ(H3:H6).
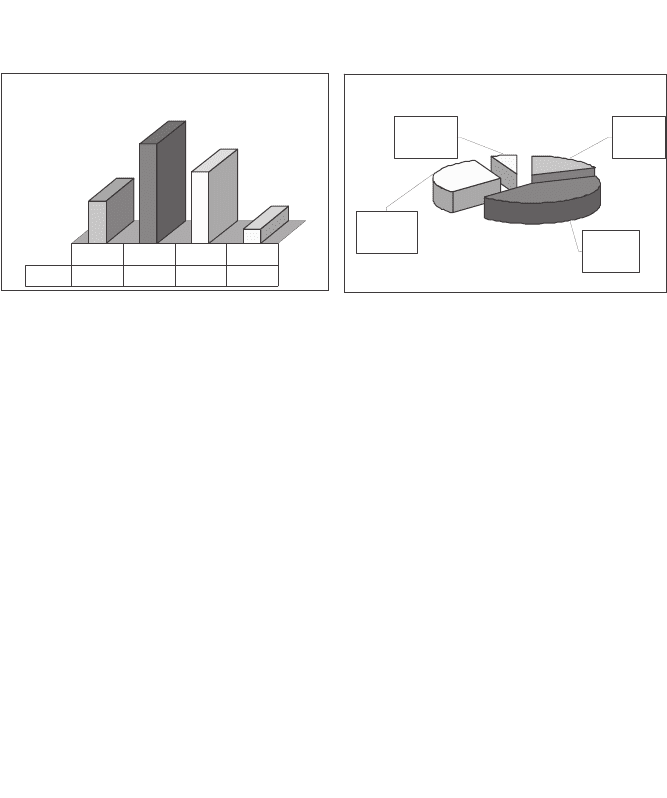
Ɋɢɫ. 2.18. Ɋɨɡɪɚɯɭɧɤɢ ɪɨɡɩɨɞɿɥɭ ɨɫɿɛ ɡɚ ɬɢɩɚɦɢ ȼɇȾ
32
əɤ ɛɚɱɢɦɨ ɡ ɪɨɡɩɨɞɿɥɭ ɨɫɿɛ ɡɚ ɬɢɩɚɦɢ ȼɇȾ (ɪɢɫ. 2.18), ɭ ɜɢɛɿɪɰɿ ɦɚɽɦɨ 3
ɨɫɨɛɢ ɡɚ ɬɢɩɨɦ «ɯɨɥɟɪɢɤ» (18,75%), 7 – ɡɚ ɬɢɩɨɦ «ɫɚɧɝɜɿɧɿɤ» (43,75%), 5 –
«ɦɟɥɚɧɯɨɥɿɤ» (31,25%) ɿ 1 – «ɮɥɟɝɦɚɬɢɤ» (6,25%).
Ⱦɥɹ ɿɥɸɫɬɪɚɰɿʀ ɚɬɪɢɛɭɬɢɜɧɢɯ ɪɨɡɩɨɞɿɥɿɜ ɜɢɤɨɪɢɫɬɨɜɭɸɬɶ ɞɜɚ ɧɚɣɛɿɥɶɲ ɪɨɡ-
ɩɨɜɫɸɞɠɟɧɿ ɬɢɩɢ ɝɪɚɮɿɤɿɜ: ɝɿɫɬɨɝɪɚɦɭ (ɪɢɫ. 2.19) ɿ ɤɪɭɝɨɜɭ ɞɿɚɝɪɚɦɭ (ɪɢɫ. 2.20).
Ɋɨɡɩɨɞɿɥ ɨɫɿɛ ɡɚ ɬɢɩɨɦ ȼɇȾ
ɑɚ ɫ ɬ ɨɬ ɢ
3751
ɏɨɥɟɪɢɤ ɋɚɧɝɜ ɿɧɿɤ Ɇɟɥɚɧɯɨ Ɏɥɟɝɦɚɬ
Ɋɨɡɩɨɞɿɥ ɨɫɿɛ ɡɚ ɬɢɩɨɦ ȼɇȾ
ɋɚɧɝɜɿɧɿɤ;
43,75%
ɏɨɥɟ ɪɢ ɤ ;
18,75%
Ɏɥɟɝɦɚɬɢɤ
; 6,25%
Ɇɟɥɚ ɧ ɯɨ ɥɿ
ɤ; 31,25%
Ɋɢɫ. 2.19. Ƚɿɫɬɨɝɪɚɦɚ ɪɨɡɩɨɞɿɥɭ Ɋɢɫ. 2.20. Ⱦɿɚɝɪɚɦɚ ɪɨɡɩɨɞɿɥɭ
Ⱥɬɪɢɛɭɬɢɜɧɿ ɪɨɡɩɨɞɿɥɢ ɞɚɸɬɶ ɦɨɠɥɢɜɿɫɬɶ ɨɰɿɧɢɬɢ ɜɥɚɫɬɢɜɨɫɬɿ ɜ ɚɛɫɨɥɸɬ-
ɧɢɯ ɿ ɜɿɞɧɨɫɧɢɯ ɡɧɚɱɟɧɧɹɯ, ɧɚɩɪɢɤɥɚɞ, ɫɩɿɜɜɿɞɧɨɲɟɧɧɹ ɪɿɡɧɢɯ ɬɢɩɿɜ ȼɇȾ, ɩɟ-
ɪɟɜɚɠɧɢɣ ɬɢɩ ȼɇȾ – ɧɚ ɝɪɚɮɿɤɚɯ ɰɟ «ɫɚɧɝɜɿɧɿɤ», ɹɤɢɣ ɫɤɥɚɞɚɽ 43,7% ɨɫɿɛ ɜɢ-
ɛɿɪɤɢ (ɪɢɫ. 2.19 ɿ 2.20).
Ɋɚɧɠɢɪɨɜɚɧɿ ɪɨɡɩɨɞɿɥɢ
Ɋɚɧɠɢɪɨɜɚɧɿ ɪɨɡɩɨɞɿɥɢ ɜɢɤɨɪɢɫɬɨɜɭɸɬɶ ɭ ɪɚɡɿ ɩɨɪɹɞɤɨɜɢɯ (ɪɚɧɝɨɜɢɯ) ɬɢ-
ɩɿɜ ɜɢɦɿɪɸɜɚɧɶ, ɧɚɩɪɢɤɥɚɞ, ɜɢɡɧɚɱɟɧɧɹ ɪɟɣɬɢɧɝɭ ɭɫɩɿɲɧɨɫɬɿ ɹɤɨʀɫɶ ɞɿɹɥɶɧɨɫɬɿ.
Ɋɚɧɠɭɜɚɧɧɹ ɩɪɢɩɭɫɤɚɽ ɞɨɦɨɜɥɟɧɿɫɬɶ ɩɪɨ ɜɿɞɩɨɜɿɞɧɿɫɬɶ ɩɟɜɧɨɝɨ ɪɚɧɝɭ ɩɟɜɧɨɦɭ
ɡɧɚɱɟɧɧɸ ɟɦɩɿɪɢɱɧɢɯ ɞɚɧɢɯ.
ɉɪɢɤɥɚɞ 2.6. ȼɢɤɨɧɚɬɢ ɪɚɧɠɭɜɚɧɧɹ ɫɬɭɞɟɧɬɿɜ ɡɚ ɪɟɡɭɥɶɬɚɬɚɦɢ ɬɟɫɬɭɜɚɧɧɹ
(ɞɢɜ. ɫɬɨɜɩɱɢɤɢ Ⱥ:ȼ ɬɚɛɥɢɰɿ ɪɢɫ. 2.21).
ɉɨɫɥɿɞɨɜɧɿɫɬɶ ɪɿɲɟɧɧɹ:
x ɭ ɤɨɦɿɪɤɭ ɋ2 ɜɧɟɫɬɢ ɦɚɬɟɦɚɬɢɱɧɢɣ ɜɢɪɚɡ, ɹɤɢɣ ɜɢɡɧɚɱɢɬɶ ɪɚɧɝ ɡɧɚɱɟɧ-
ɧɹ ɤɨɦɿɪɤɢ ȼ2 ɫɟɪɟɞ ɞɚɧɢɯ ɜɢɛɿɪɤɢ ɜ ɞɿɚɩɚɡɨɧɿ ȼ$2:ȼ$10:
=ɋɑȬɌ(B$2:B$10) + 1–((ɋɑȬɌ(B$2:B$10) + 1– ɊȺɇȽ(B2;B$2:B$10;
1) – ɊȺɇȽ(B2;B$2:B$10; 0))/2+ɊȺɇȽ(B2;B$2:B$10;1));
33
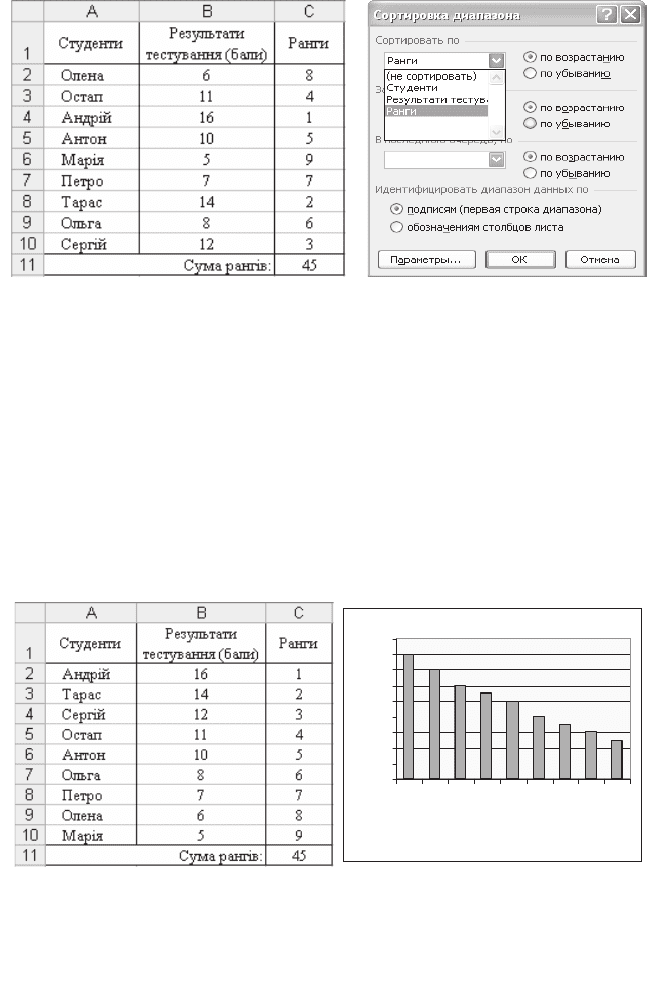
Ɋɢɫ. 2.21. Ɋɚɧɝɢ ɫɬɭɞɟɧɬɿɜ ɡɚ
ɪɟɡɭɥɶɬɚɬɚɦɢ ɬɟɫɬɭɜɚɧɧɹ
Ɋɢɫ. 2.22. Ⱦɿɚɥɨɝɨɜɟ ɜɿɤɧɨ
«ɋɨɪɬɭɜɚɧɧɹ ɞɿɚɩɚɡɨɧɭ»
x ɫɤɨɩɿɸɜɚɬɢ ɚɧɚɥɨɝɿɱɧɿ ɜɢɪɚɡɢ ɭ ɤɨɦɿɪɤɢ ɋ3:ɋ10;
x ɭ ɤɨɦɿɪɤɭ ɋ11 ɜɧɟɫɬɢ ɜɢɪɚɡ =ɋɍɆɆ(C2:C10), ɹɤɢɣ ɞɚɫɬɶ ɫɭɦɭ ɪɚɧɝɿɜ;
x ɭɩɨɪɹɞɤɭɜɚɬɢ ɞɚɧɿ ɞɿɚɩɚɡɨɧɭ Ⱥ2:ɋ10 ɡɚ ɪɚɧɝɨɦ ɡɚ ɞɨɩɨɦɨɝɨɸ ɤɨɦɚɧɞ ɝɨɥɨ-
ɜɧɨɝɨ ɦɟɧɸ MS Excel [Ⱦɚɧɿ –> ɋɨɪɬɭɜɚɧɧɹ] ɿ ɞɿɚɥɨɝɨɜɨɝɨ ɜɿɤɧɚ (ɪɢɫ. 2.22);
x ɨɬɪɢɦɚɬɢ ɭɩɨɪɹɞɤɨɜɚɧɿ ɫɬɨɜɩɱɢɤɢ ɬɚɛɥɢɰɿ ɡɚ ɪɚɧɝɨɦ (ɪɢɫ. 2.23);
x ɜɿɞɨɛɪɚɡɢɬɢ ɪɟɣɬɢɧɝɨɜɢɣ ɫɩɢɫɨɤ ɫɬɭɞɟɧɬɿɜ ɝɪɚɮɿɱɧɨ (ɪɢɫ. 2.24).
Ɋɟɣɬɢɧɝɢ ɫɬɭɞɟɧɬɿɜ
8
10
12
16
6
7
11
14
5
0
2
4
6
8
10
12
14
16
18
Ⱥɧɞɪɿɣ
Ɍɚɪɚɫ
ɋɟɪɝɿɣ
Ɉɫɬɚɩ
Ⱥɧɬɨɧ
Ɉɥɶɝɚ
ɉɟɬɪɨ
Ɉɥɟɧɚ
Ɇɚɪɿɹ
ɋɬɭɞɟɧɬɢ
Ȼɚɥɢ ɬɟɫɬɭɜɚɧɧ
ɹ
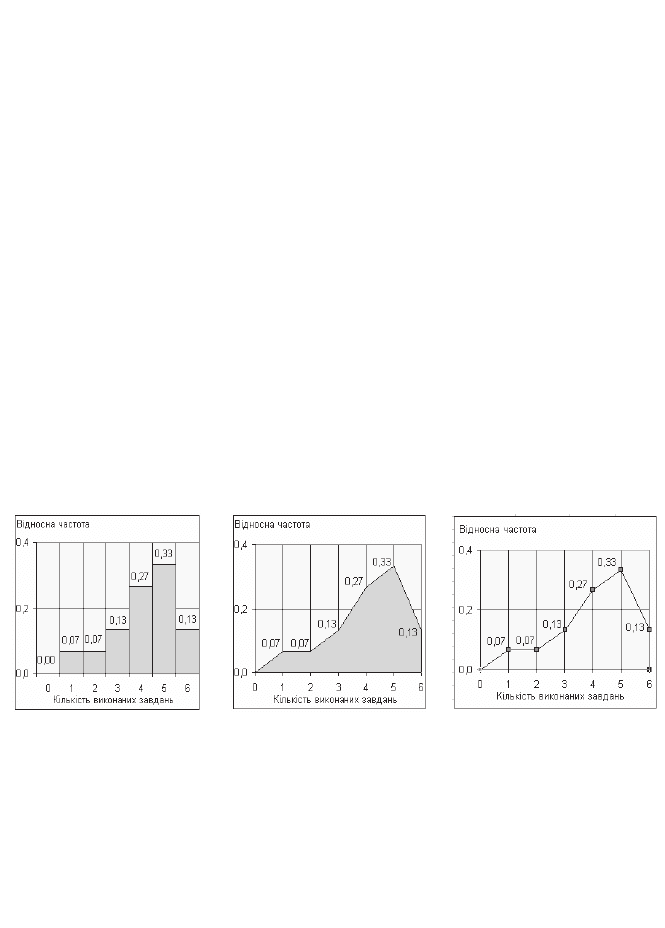
Ɋɢɫ. 2.23. ɍɩɨɪɹɞɤɨɜɚɧɿ ɞɚɧɿ
ɡɚ ɪɚɧɝɨɦ
Ɋɢɫ. 2.24. Ɋɟɣɬɢɧɝɨɜɢɣ ɫɩɢɫɨɤ
ɫɬɭɞɟɧɬɿɜ
Ɋɚɧɠɢɪɨɜɚɧɿ ɪɨɡɩɨɞɿɥɢ ɞɚɸɬɶ ɦɨɠɥɢɜɿɫɬɶ ɧɚɨɱɧɨʀ ɜɿɡɭɚɥɿɡɚɰɿʀ ɪɟɡɭɥɶɬɚɬɿɜ
34
ɞɨɫɥɿɞɠɟɧɶ ɩɟɜɧɨʀ ɜɥɚɫɬɢɜɨɫɬɿ ɫɟɪɟɞ ɨɛ’ɽɤɬɿɜ ɞɨɫɥɿɞɠɟɧɧɹ ɭ ɧɚɩɪɹɦɚɯ ʀɯ ɡɛɿ-
ɥɶɲɟɧɧɹ ɚɛɨ ɡɦɟɧɲɟɧɧɹ.
Ɉɫɧɨɜɧɢɦɢ ɫɩɨɫɨɛɚɦɢ ɩɪɟɞɫɬɚɜɥɟɧɧɹ ɟɦɩɿɪɢɱɧɢɯ ɪɨɡɩɨɞɿɥɿɜ ɽ ɬɚɛɥɢɱ-
ɧɢɣ, ɝɪɚɮɿɱɧɢɣ ɬɚ ɚɧɚɥɿɬɢɱɧɢɣ.
Ɍɚɛɥɢɱɧɢɣ ɫɩɨɫɿɛ ɩɪɟɞɫɬɚɜɥɟɧɧɹ ɪɨɡɩɨɞɿɥɿɜ ɩɪɨɞɟɦɨɧɫɬɪɨɜɚɧɨ, ɧɚɩɪɢ-
ɤɥɚɞ, ɧɚ ɪɢɫ. 2.16. ɉɨ-ɪɿɡɧɨɦɭ ɧɚɡɢɜɚɸɬɶ ɬɚɤɿ ɬɚɛɥɢɰɿ: ɬɚɛɥɢɰɟɸ ɟɦɩɿɪɢɱɧɢɯ
ɱɚɫɬɨɬ ɚɛɨ ɬɚɛɥɢɱɧɨɸ ɮɨɪɦɨɸ ɩɪɟɞɫɬɚɜɥɟɧɧɹ ɪɨɡɩɨɞɿɥɭ. Ɍɚɛɥɢɱɧɢɣ ɫɩɨɫɿɛ
ɽ ɨɫɧɨɜɧɢɦ ɪɨɡɪɚɯɭɧɤɨɜɢɦ ɦɟɬɨɞɨɦ ɿ ɩɟɪɟɞɭɦɨɜɨɸ ɣɨɝɨ ɝɪɚɮɿɱɧɨʀ ɮɨɪɦɢ.
Ɋɚɡɨɦ ɜɨɧɢ ɞɚɸɬɶ ɰɿɥɿɫɧɟ ɭɹɜɥɟɧɧɹ ɳɨɞɨ ɜɥɚɫɬɢɜɨɫɬɟɣ ɜɢɛɿɪɤɢ.
Ƚɪɚɮɿɱɧɢɣ ɫɩɨɫɿɛ ɩɪɟɞɫɬɚɜɥɟɧɧɹ – ɰɟ ɜɿɞɨɛɪɚɠɟɧɧɹ ɪɨɡɩɨɞɿɥɭ ɝɪɚɮɿɱ-
ɧɢɦɢ ɡɚɫɨɛɚɦɢ, ɫɟɪɟɞ ɹɤɢɯ ɧɚɣɩɨɲɢɪɟɧɿɲɢɦɢ ɽ ɝɿɫɬɨɝɪɚɦɚ, ɩɨɥɿɝɨɧ ɿ ɥɿɧɿɣ-
ɧɢɣ ɝɪɚɮɿɤ. ɇɚ ɪɢɫ. 2.25 – 2.27 ɩɨɤɚɡɚɧɨ ɞɢɮɟɪɟɧɰɿɚɥɶɧɢɣ ɜɿɞɧɨɫɧɢɣ ɪɨɡɩɨɞɿɥ
ɧɟɡɝɪɭɩɨɜɚɧɢɯ ɱɚɫɬɨɬ ɭ ɬɪɶɨɯ ɜɚɪɿɚɧɬɚɯ. Ʉɨɦɛɿɧɨɜɚɧɿ ɫɩɨɫɨɛɢ ɩɪɟɞɫɬɚɜɥɟɧɧɹ,
ɹɤɿ ɨɛ'ɽɞɧɭɸɬɶ ɭ ɦɟɠɚɯ ɨɞɧɿɽʀ ɝɪɚɮɿɱɧɨʀ ɮɨɪɦɢ ɪɿɡɧɿ ɬɢɩɢ ɪɨɡɩɨɞɿɥɭ (ɞɢɮɟɪɟ-
ɧɰɿɚɥɶɧɢɣ ɬɚ ɿɧɬɟɝɪɚɥɶɧɢɣ), ɦɨɠɧɚ ɩɨɛɚɱɢɬɢ ɧɚ ɪɢɫ. 2.17.
Ɋɢɫ. 2.25.
Ƚɿɫɬɨɝɪɚɦɚ
Ɋɢɫ. 2.26.
ɉɨɥɿɝɨɧ
Ɋɢɫ. 2.27.
Ʌɿɧɿɣɧɢɣ ɝɪɚɮɿɤ
Ⱥɧɚɥɿɬɢɱɧɢɣ ɫɩɨɫɿɛ ɩɪɟɞɫɬɚɜɥɟɧɧɹ ɩɟɪɟɞɛɚɱɚɽ ɜɢɤɨɪɢɫɬɚɧɧɹ ɦɚɬɟɦɚ-
ɬɢɱɧɨʀ ɟɦɩɿɪɢɱɧɨʀ ɮɭɧɤɰɿʀ ɪɨɡɩɨɞɿɥɭ, ɧɚɩɪɢɤɥɚɞ, ɳɿɥɶɧɨɫɬɿ f(x
i
), ɚɛɨ ɪɨɡɩɨɞɿ-
ɥɭ F(x
i
). Ɍɚɤ, ɳɿɥɶɧɿɫɬɶ ɪɨɡɩɨɞɿɥɭ ɡ ɪɢɫ. 2.25 – ɦɨɠɧɚ ɩɪɟɞɫɬɚɜɢɬɢ ɡɚ ɞɨɩɨ-
ɦɨɝɨɸ ɟɦɩɿɪɢɱɧɨʀ ɮɭɧɤɰɿʀ:

35
°
°
°
°
°
¯
°
°
°
°
°
®
.6,13.0
;5,33.0
;4,27.0
;3,13.0
;2,07.0
;1,07.0
;0,00.0
)(
x
x
x
x
x
x
x
xf
i
Ⱥɧɚɥɨɝɿɱɧɨ ɦɨɠɧɚ ɩɪɟɞɫɬɚɜɥɹɬɢ ɣ ɪɨɡɩɨɞɿɥɢ ɿɧɬɟɝɪɚɥɶɧɢɯ ɱɚɫɬɨɬ. ɋɬɚɬɢ-
ɫɬɢɱɧɿ ɪɨɡɩɨɞɿɥɢ ɽ ɩɟɪɜɢɧɧɨɸ ɛɚɡɨɸ, ɧɚɜɤɨɥɨ ɹɤɨʀ ɨɛ'ɽɞɧɭɸɬɶɫɹ ɨɫɧɨɜɧɿ ɦɟ-
ɬɨɞɢ ɦɚɬɟɦɚɬɢɱɧɨʀ ɫɬɚɬɢɫɬɢɤɢ.
Ɂɚɩɢɬɚɧɧɹ. Ɂɚɜɞɚɧɧɹ.
1. Ɉɯɚɪɚɤɬɟɪɢɡɭɣɬɟ ɨɫɧɨɜɧɿ ɝɪɭɩɢ ɫɬɚɬɢɫɬɢɱɧɢɯ ɩɨɤɚɡɧɢɤɿɜ ɜɢɛɿɪɤɢ.
2. ɓɨ ɬɚɤɟ ɜɚɪɿɚɰɿɣɧɢɣ ɪɹɞ ɿ ɫɬɚɬɢɫɬɢɱɧɢɣ ɪɨɡɩɨɞɿɥ?
3. ɑɢɦ ɜɿɞɪɿɡɧɹɸɬɶɫɹ ɦɿɠ ɫɨɛɨɸ ɜɚɪɿɚɰɿɣɧɿ, ɚɬɪɢɛɭɬɢɜɧɿ ɬɚ ɪɚɧɠɢɪɭɜɚɧɿ
ɪɨɡɩɨɞɿɥɢ?
4. əɤɚ ɪɿɡɧɢɰɹ ɦɿɠ ɚɛɫɨɥɸɬɧɢɦɢ ɿ ɜɿɞɧɨɫɧɢɦɢ ɪɨɡɩɨɞɿɥɚɦɢ ɱɚɫɬɨɬ?
5. əɤ ɪɨɡɪɚɯɨɜɭɸɬɶɫɹ ɧɟɡɝɪɭɩɨɜɚɧɿ ɿ ɡɝɪɭɩɨɜɚɧɿ ɪɨɡɩɨɞɿɥɢ ɱɚɫɬɨɬ?
6. ɑɢɦ ɜɿɞɪɿɡɧɹɸɬɶɫɹ ɞɢɮɟɪɟɧɰɿɚɥɶɧɿ ɬɚ ɿɧɬɟɝɪɚɥɶɧɿ ɪɨɡɩɨɞɿɥɢ ɱɚɫɬɨɬ?
7. əɤɿ ɬɢɩɢ ɝɪɚɮɿɤɿɜ ɪɨɡɩɨɞɿɥɭ ɱɚɫɬɨɬ ɜɜɚɠɚɸɬɶɫɹ ɧɚɣɩɨɲɢɪɟɧɿɲɢɦɢ?
8. ɉɨɜɬɨɪɿɬɶ ɦɚɬɟɦɚɬɢɱɧɿ ɩɪɨɰɟɞɭɪɢ ɡɚɜɞɚɧɶ ɡɚ ɩɪɢɤɥɚɞɚɦɢ 2.1 – 2.6.
9. ȼɢɤɨɧɚɣɬɟ ɥɚɛɨɪɚɬɨɪɧɿ ɪɨɛɨɬɢ ʋ 1 ɿ ʋ 2.
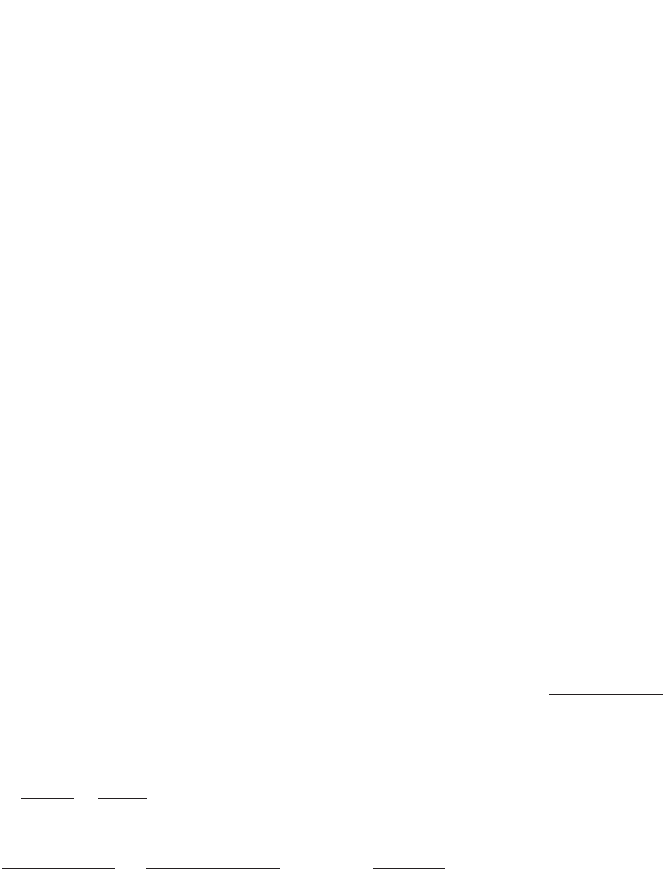
36
2.2. ɉɈɄȺɁɇɂɄɂ ȼɂȻȱɊɄɂ
Ɇɿɪɢ ɰɟɧɬɪɚɥɶɧɨʀ ɬɟɧɞɟɧɰɿʀ (ɆɐɌ)
Ɇɿɪɚɦɢ ɰɟɧɬɪɚɥɶɧɨʀ ɬɟɧɞɟɧɰɿʀ
(ɆɐɌ) ɧɚɡɢɜɚɸɬɶ ɱɢɫɟɥɶɧɿ ɩɨɤɚɡɧɢɤɢ
ɬɢɩɨɜɢɯ ɜɥɚɫɬɢɜɨɫɬɟɣ ɟɦɩɿɪɢɱɧɢɯ ɞɚɧɢɯ. ɐɿ ɩɨɤɚɡɧɢɤɢ ɞɚɸɬɶ ɜɿɞɩɨɜɿɞɿ ɧɚ
ɩɢɬɚɧɧɹ ɩɪɨ ɬɟ, ɧɚɩɪɢɤɥɚɞ, «ɹɤɢɣ ɫɟɪɟɞɧɿɣ ɪɿɜɟɧɶ ɿɧɬɟɥɟɤɬɭ ɫɬɭɞɟɧɬɿɜ ɩɟɞɚɝɨ-
ɝɿɱɧɨɝɨ ɭɧɿɜɟɪɫɢɬɟɬɭ?», «ɹɤɟ ɬɢɩɨɜɟ ɡɧɚɱɟɧɧɹ ɩɨɤɚɡɧɢɤɚ ɜɿɞɩɨɜɿɞɚɥɶɧɨɫɬɿ ɩɟ-
ɜɧɨʀ ɝɪɭɩɢ ɨɫɿɛ?». ȱɫɧɭɽ ɩɨɪɿɜɧɹɧɨ ɧɟɜɟɥɢɤɚ ɤɿɥɶɤɿɫɬɶ ɬɚɤɢɯ ɩɨɤɚɡɧɢɤɿɜ-ɦɿɪ ɿ
ɜ ɩɟɪɲɭ ɱɟɪɝɭ:
ɦɨɞɚ, ɦɟɞɿɚɧɚ, ɫɟɪɟɞɧɽ ɚɪɢɮɦɟɬɢɱɧɟ. Ʉɨɠɧɚ ɤɨɧɤɪɟɬɧɚ ɆɐɌ
ɦɚɽ ɫɜɨʀ ɨɫɨɛɥɢɜɨɫɬɿ, ɳɨ ɪɨɛɥɹɬɶ ʀʀ ɰɿɧɧɨɸ ɞɥɹ ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ ɨɛ'ɽɤɬɚ ɞɨɫɥɿ-
ɞɠɟɧɧɹ ɜ ɩɟɜɧɢɯ ɭɦɨɜɚɯ.
Ɇɨɞɚ
Mo – ɰɟ ɡɧɚɱɟɧɧɹ, ɹɤɟ ɧɚɣɱɚɫɬɿɲɟ ɬɪɚɩɥɹɽɬɶɫɹ ɫɟɪɟɞ ɟɦɩɿɪɢɱɧɢɯ
ɞɚɧɢɯ. Ɍɚɤ, ɞɥɹ ɪɹɞɭ ɡɧɚɱɟɧɶ 2, 2, 3, 3, 3, 3, 4, 4, 4, 5, 5 ɦɨɞɚ ɞɨɪɿɜɧɸɽ 3 (
Mo =
3). Ɂɜɟɪɧɿɬɶ ɭɜɚɝɭ ɧɚ ɬɟ, ɳɨ ɦɨɞɚ ɽ ɡɧɚɱɟɧɧɹ ɡ ɧɚɣɛɿɥɶɲɨɸ ɱɚɫɬɨɬɨɸ (ɭ ɩɪɢ-
ɤɥɚɞɿ ɰɟ ɡɧɚɱɟɧɧɹ ɞɨɪɿɜɧɸɽ 3), ɚ ɧɟ ɱɚɫɬɨɬɚ ɰɶɨɝɨ ɡɧɚɱɟɧɧɹ (ɭ ɩɪɢɤɥɚɞɿ ɜɨɧɚ
ɞɨɪɿɜɧɸɽ 4).
ɉɪɢ ɜɢɡɧɚɱɟɧɧɿ ɦɨɞɢ ɧɟɨɛɯɿɞɧɨ ɞɨɬɪɢɦɭɜɚɬɢɫɹ ɬɚɤɢɯ ɭɝɨɞ:
x ɦɨɞɚ ɦɨɠɟ ɛɭɬɢ ɜɿɞɫɭɬɧɹ, ɧɚɩɪɢɤɥɚɞ, ɞɥɹ ɞɚɧɢɯ 2, 2, 3, 3, 4, 4, 5, 5;
x ɹɤɳɨ ɜɚɪɿɚɧɬɢ ɫɭɦɿɠɧɿ ɿ ɦɚɸɬɶ ɨɞɧɚɤɨɜɭ ɱɚɫɬɨɬɭ, ɦɨɞɚ ɜɢɡɧɚɱɚɽɬɶɫɹ ɹɤ
ɫɟɪɟɞɧɽ ɡɧɚɱɟɧɧɹ ɫɭɫɿɞɧɿɯ ɜɚɪɿɚɧɬ. ɇɚɩɪɢɤɥɚɞ, ɞɥɹ ɪɹɞɭ 2, 2, 3, 4, 4, 4, 5, 5, 5
ɦɨɞɚ
Ɇɨ = (4+5)/2=4,5;
x ɹɤɳɨ ɜɚɪɿɚɧɬɢ ɧɟɫɭɦɿɠɧɿ, ɦɨɠɟ ɿɫɧɭɜɚɬɢ ɞɟɤɿɥɶɤɚ ɦɨɞ. Ɍɚɤ, ɞɥɹ ɞɚɧɢɯ 2,
2, 3, 3, 3, 4, 5, 5, 5 ɯɚɪɚɤɬɟɪɧɚ ɛɿɦɨɞɚɥɶɧɿɫɬɶ, ɬɨɛɬɨ ɞɜɿ ɦɨɞɢ Ɇɨ
1
= 3 ɿ Ɇɨ
2
= 5;
x ɟɦɩɿɪɢɱɧɿ ɞɚɧɿ ɦɨɠɭɬɶ ɦɚɬɢ ɜɟɥɢɤɿ ɬɚ ɦɚɥɿ ɦɨɞɢ. ɇɚɩɪɢɤɥɚɞ, ɞɚɧɿ 2, 2,
3, 3, 3, 4, 4, 4
, 5, 6, 6, 6, 6, 6, 6, 6, 7, 7, 7, 8, 9, 9, 9, 9 ɦɚɸɬɶ ɨɞɧɭ ɜɟɥɢɤɭ ɦɨɞɭ
Ɇɨ
1
= 6 ɬɚ ɞɜɿ ɦɚɥɿ ɦɨɞɢ Ɇɨ
2
= 3,5 ɿ Ɇɨ
3
= 9.
ɇɚ ɝɪɚɮɿɤɚɯ ɪɨɡɩɨɞɿɥɭ
ɦɨɞɚ – ɰɟ ɜɚɪɿɚɧɬɚ ɡ ɦɚɤɫɢɦɚɥɶɧɨɸ ɱɚɫɬɨɬɨɸ. ɇɚ
ɪɢɫ. 2.25 ɜɚɪɿɚɧɬɚ
ɯ
6
=5 ɦɚɽ ɧɚɣɛɿɥɶɲɭ ɱɚɫɬɨɬɭ (0,33), ɬɨɦɭ ɿ ɽ ɦɨɞɨɸ Ɇɨ = 5.
Ɇɟɞɿɚɧɚ
Md – ɰɟ ɡɧɚɱɟɧɧɹ, ɹɤɟ ɩɪɢɯɨɞɢɬɶɫɹ ɧɚ ɫɟɪɟɞɢɧɭ ɭɩɨɪɹɞɤɨɜɚɧɨʀ

37
ɩɨɫɥɿɞɨɜɧɨɫɬɿ ɟɦɩɿɪɢɱɧɢɯ ɞɚɧɢɯ. Ⱦɥɹ ɧɟɩɚɪɧɨʀ ɤɿɥɶɤɨɫɬɿ ɞɚɧɢɯ ɦɟɞɿɚɧɚ ɜɢ-
ɡɧɚɱɚɽɬɶɫɹ ɫɟɪɟɞɧɿɦ ɟɥɟɦɟɧɬɨɦ
2/)1(
n
xMd
. ɇɚɩɪɢɤɥɚɞ, ɞɥɹ 11 ɡɧɚɱɟɧɶ 4, 4,
4, 5, 5, 5,
5, 5, 6, 6, 7 ɦɟɞɿɚɧɚ ɞɨɪɿɜɧɸɽ 4 (Ɇd = 5), ɬɨɛɬɨ:
5
62/)111(2/)1(
xxxMd
n
.
əɤɳɨ ɤɿɥɶɤɿɫɬɶ ɡɧɚɱɟɧɶ ɞɚɧɢɯ ɽ
ɩɚɪɧɨɸ, ɬɨ ɦɟɞɿɚɧɨɸ ɽ ɫɟɪɟɞɧɽ ɡɧɚɱɟɧɧɹ
ɰɟɧɬɪɚɥɶɧɢɯ ɫɭɫɿɞɧɿɯ ɟɥɟɦɟɧɬɿɜ:
2
12/2/
nn
xx
Md
. ɇɚɩɪɢɤɥɚɞ, ɞɥɹ 12 ɡɧɚ-
ɱɟɧɶ 3, 3, 3, 4, 4, 5
, 6, 6, 6, 6, 7, 7 ɦɟɞɿɚɧɚ Ɇd = (5+6)/2 = 5,5:
5,5
2
11
2
65
222
7612/122/1212/2/
xxxxxx
Md
nn
.
ɋɟɪɟɞɧɽ ɚɪɢɮɦɟɬɢɱɧɟ
X
(ɜɢɛɿɪɤɨɜɟ ɫɟɪɟɞɧɽ ɚɛɨ ɫɟɪɟɞɧɽ) ɫɭɤɭɩɧɨɫɬɿ n
ɡɧɚɱɟɧɶ ɞɨɪɿɜɧɸɽ:
n
xxx
X
n
!
21
. (2.1)
ȼɢɤɨɪɢɫɬɨɜɭɸɬɶ ɿɧɲɿ ɮɨɪɦɭɥɢ, ɧɚɩɪɢɤɥɚɞ,
¦
n
i
i
x
n
X
1
1
ɫɤɨɪɨɱɟɧɨ
¦
i
x
n
X
1
.
Ɍɚɤ, ɞɥɹ ɜɢɛɿɪɤɢ (2, 2, 3, 3, 4, 5, 6, 7, 7, 8)
ɫɟɪɟɞɧɽ X ɞɨɪɿɜɧɸɜɚɬɢɦɟ:
7,410/4710/)8776543322( X
.
əɤɳɨ ɞɚɧɿ ɩɪɟɞɫɬɚɜɥɟɧɨ ɪɨɡɩɨɞɿɥɚɦɢ ɱɚɫɬɨɬ, ɫɟɪɟɞɧɽ ɜɢɡɧɚɱɚɽɬɶɫɹ ɹɤ:
¦
¦
i
ii
f
xf
X
, (2.2)
ɞɟ
x
ɿ
– ɜɚɪɿɚɧɬɢ ɧɟɡɝɪɭɩɨɜɚɧɢɯ ɱɚɫɬɨɬ ɚɛɨ ɰɟɧɬɪɚɥɶɧɿ ɡɧɚɱɟɧɧɹ ɤɥɚɫɨɜɢɯ
ɿɧɬɟɪɜɚɥɿɜ ɭ ɪɚɡɿ ɡɝɪɭɩɨɜɚɧɢɯ ɱɚɫɬɨɬ; f
ɿ
– ɞɢɮɟɪɟɧɰɿɚɥɶɧɿ ɱɚɫɬɨɬɢ.
Ɉɫɨɛɥɢɜɨɫɬɿ ɦɿɪ ɰɟɧɬɪɚɥɶɧɨʀ ɬɟɧɞɟɧɰɿʀ:
x ɦɨɞɚ ɜɢɛɿɪɤɢ ɨɛɱɢɫɥɸɽɬɶɫɹ ɩɪɨɫɬɨ, ʀʀ ɦɨɠɧɚ ɜɢɡɧɚɱɢɬɢ «ɧɚ ɨɤɨ». Ⱦɥɹ
ɞɭɠɟ ɜɟɥɢɤɢɯ ɝɪɭɩ ɞɚɧɢɯ ɦɨɞɚ ɽ ɞɨɫɢɬɶ ɫɬɚɛɿɥɶɧɨɸ ɦɿɪɨɸ ɰɟɧɬɪɭ ɪɨɡɩɨɞɿɥɭ;
x ɦɟɞɿɚɧɚ ɡɚɣɦɚɽ ɩɪɨɦɿɠɧɟ ɩɨɥɨɠɟɧɧɹ ɦɿɠ ɦɨɞɨɸ ɿ ɫɟɪɟɞɧɿɦ ɡ ɩɨɝɥɹɞɭ ʀʀ
ɩɿɞɪɚɯɭɧɤɭ. ɐɹ ɦɿɪɚ ɨɫɨɛɥɢɜɨ ɥɟɝɤɨ ɜɢɡɧɚɱɚɽɬɶɫɹ ɭ ɪɚɡɿ ɪɚɧɠɢɪɨɜɚɧɢɯ ɞɚɧɢɯ;
x ɫɟɪɟɞɧɽ ɚɪɢɮɦɟɬɢɱɧɟ ɩɟɪɟɞɛɚɱɚɽ ɜɢɤɨɪɢɫɬɨɜɭɜɚɧɧɹ ɜɫɿɯ ɡɧɚɱɟɧɶ ɜɢɛɿɪ-
ɤɢ, ɩɪɢɱɨɦɭ ɜɫɿ ɜɨɧɢ ɜɩɥɢɜɚɸɬɶ ɧɚ ɡɧɚɱɟɧɧɹ ɰɿɽʀ ɦɿɪɢ.

38
Ɋɨɡɝɥɹɧɟɦɨ, ɳɨ ɦɨɠɟ ɜɿɞɛɭɬɢɫɹ ɡ ɦɨɞɨɸ, ɦɟɞɿɚɧɨɸ ɿ ɫɟɪɟɞɧɿɦ, ɤɨɥɢ ɡɦɿ-
ɧɢɬɶɫɹ ɭɞɜɿɱɿ ɥɢɲɟ ɨɞɧɟ ɡɧɚɱɟɧɧɹ, ɧɚɩɪɢɤɥɚɞ, 10-ɝɨ ɨɛ'ɽɤɬɚ ɜɢɛɿɪɤɢ (ɪɢɫ. 2.28).
Ɋɢɫ. 2.28. ȼɥɚɫɬɢɜɨɫɬɿ ɆɐɌ
əɤ ɛɚɱɢɦɨ, ɦɨɞɚ ɿ ɦɟɞɿɚɧɚ ɡɚɥɢɲɢɥɢɫɹ ɧɟɡɦɿɧɧɢɦɢ, ɭ ɬɨɣ ɱɚɫ ɹɤ ɫɟɪɟɞɧɽ
ɡɦɿɧɢɥɨɫɹ ɡɧɚɱɧɨɸ ɦɿɪɨɸ (ɡ 4,8 ɞɨ 5,7). ɇɚ ɜɟɥɢɱɢɧɭ ɫɟɪɟɞɧɶɨɝɨ ɨɫɨɛɥɢɜɨ
ɫɭɬɬɽɜɨ ɜɩɥɢɜɚɸɬɶ ɡɧɚɱɟɧɧɹ, ɳɨ ɩɟɪɟɛɭɜɚɸɬɶ ɞɚɥɟɤɨ ɜɿɞ ɰɟɧɬɪɭ ɝɪɭɩɢ ɞɚɧɢɯ.
Ɂ ɬɨɱɤɢ ɡɨɪɭ ɩɨɦɢɥɨɤ, ɳɨ ɜɢɧɢɤɚɸɬɶ ɱɟɪɟɡ ɬɟ, ɤɨɥɢ ɞɥɹ ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ
ɰɿɥɨʀ ɫɭɤɭɩɧɨɫɬɿ ɜɢɛɢɪɚɽɬɶɫɹ ɥɢɲɟ ɨɞɧɚ
ɽɞɢɧɚ ɫɬɚɬɢɫɬɢɱɧɚ ɦɿɪɚ (ɦɨɞɚ, ɦɟɞɿ-
ɚɧɚ
ɱɢ ɫɟɪɟɞɧɽ), ɤɨɠɧɚ ɦɿɪɚ ɰɟɧɬɪɚɥɶɧɨʀ ɬɟɧɞɟɧɰɿʀ ɦɚɽ ɫɜɨɸ ɿɧɬɟɪɩɪɟɬɚɰɿɸ
Ɇɨɞɚ ɽ ɧɚɣɛɿɥɶɲ ɩɪɟɞɫɬɚɜɧɢɰɶɤɢɦ ɡɧɚɱɟɧɧɹɦ ɚɛɨ ɡɧɚɱɟɧɧɹɦ, ɹɤɟ ɧɚɣ-
ɤɪɚɳɟ
«ɡɚɦɿɧɸɽ ɜɫɿ ɡɧɚɱɟɧɧɹ», ɹɤɳɨ ɦɢ ɡɦɭɲɟɧɿ ɜɢɛɪɚɬɢ ɨɞɧɟ.
Ɇɟɞɿɚɧɚ – ɰɟ ɬɚɤɟ ɡɧɚɱɟɧɧɹ, ɞɥɹ ɹɤɨɝɨ ɫɭɦɚ ɚɛɫɨɥɸɬɧɢɯ ɪɿɡɧɢɰɶ ɭɫɿɯ ɡɧɚ-
ɱɟɧɶ
ɦɟɧɲɚ ɡɚ ɫɭɦɭ ɪɿɡɧɢɰɶ ɞɥɹ ɛɭɞɶ-ɹɤɨɝɨ ɿɧɲɨɝɨ ɡɧɚɱɟɧɧɹ. ɇɚɩɪɢɤɥɚɞ, ɞɥɹ
ɫɭɤɭɩɧɨɫɬɿ {1, 3, 6, 8, 9} ɦɟɞɿɚɧɚ Md = 6. Ⱥɛɫɨɥɸɬɧɿ ɪɿɡɧɢɰɿ ɫɬɚɧɨɜɥɹɬɶ: |1–
6|=5, |3–6|=3, |6–6|=0, |8–6|=2, |9–6|=3. ɋɭɦɚ ɜɫɿɯ ɰɢɯ ɪɿɡɧɢɰɶ 5+3+0+2+3=13
ɦɟɧɲɚ ɡɚ ɫɭɦɭ ɪɿɡɧɢɰɶ ɳɨɞɨ ɛɭɞɶ-ɹɤɨɝɨ ɿɧɲɨɝɨ ɡɧɚɱɟɧɧɹ. ɇɚɩɪɢɤɥɚɞ, ɞɥɹ 1
ɚɛɫɨɥɸɬɧɿ ɪɿɡɧɢɰɿ |1–1|=0, |3–1|=2, |6–1|=5, |8–1|=7, |9–1|=8, ɚ ʀɯɧɹ ɫɭɦɚ
0+2+5+7+8=22. ȱɧɲɿ ɪɨɡɪɚɯɭɧɤɢ ɞɚɞɭɬɶ ɩɨɞɿɛɧɿ ɪɟɡɭɥɶɬɚɬɢ.
əɤɳɨ ɜɢɛɪɚɬɢ ɦɟɞɿɚɧɭ, ɬɨ ɞɨɫɹɝɚɽɬɶɫɹ ɦɿɧɿɦɚɥɶɧɟ ɜɿɞɯɢɥɟɧɧɹ – ɡɚ ɭɦɨɜɢ,
ɳɨ «ɜɿɞɯɢɥɟɧɧɹ» ɜɢɡɧɚɱɚɽɬɶɫɹ ɹɤ
ɫɭɦɚ ɚɛɫɨɥɸɬɧɨʀ ɜɿɞɦɿɧɧɨɫɬɿ ɤɨɠɧɨɝɨ ɡɧɚ-
ɱɟɧɧɹ ɜɿɞ ɦɟɞɿɚɧɧɨʀ ɨɰɿɧɤɢ. əɤɳɨ ɠ ɡɚɦɿɫɬɶ ɤɨɠɧɨɝɨ ɡɧɚɱɟɧɧɹ ɛɟɪɟɬɶɫɹ
ɫɟɪɟ-
ɞɧɽ
, ɡɚɛɟɡɩɟɱɭɽɬɶɫɹ ɦɿɧɿɦɚɥɶɧɟ ɜɿɞɯɢɥɟɧɧɹ – ɡɚ ɭɦɨɜɢ, ɳɨ «ɜɿɞɯɢɥɟɧɧɹ» ɜɢ-
ɡɧɚɱɚɽɬɶɫɹ ɹɤ
ɫɭɦɚ ɤɜɚɞɪɚɬɿɜ ɪɿɡɧɢɰɶ ɤɨɠɧɨɝɨ ɡɧɚɱɟɧɧɹ ɡ ɫɟɪɟɞɧɿɦ.
ȼɢɤɨɪɢɫɬɚɧɧɹ ɦɿɪ ɰɟɧɬɪɚɥɶɧɨʀ ɬɟɧɞɟɧɰɿʀ ɭ ɹɤɨɫɬɿ ɯɚɪɚɤɬɟɪɢɫɬɢɤ ɜɢɩɚɞɤɨɜɨʀ
ɜɢɛɿɪɤɢ ɽ ɭɦɨɜɨɸ ɧɟɨɛɯɿɞɧɨɸ, ɚɥɟ ɧɟɞɨɫɬɚɬɧɶɨɸ. ɉɨɤɚɡɧɢɤɢ ɨɩɢɫɨɜɨʀ ɫɬɚɬɢɫ-
ɬɢɤɢ, ɤɪɿɦ ɆɐɌ, ɜɤɥɸɱɚɸɬɶ ɳɟ ɨɞɧɭ ɝɪɭɩɭ ɩɨɤɚɡɧɢɤɿɜ –
ɦɿɪɢ ɦɿɧɥɢɜɨɫɬɿ (ɆɆ).
39
Ɇɿɪɢ ɦɿɧɥɢɜɨɫɬɿ (ɆɆ)
Ɉɛɦɟɠɟɧɿɫɬɶ ɦɿɪ ɰɟɧɬɪɚɥɶɧɨʀ ɬɟɧɞɟɧɰɿʀ ɞɥɹ ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ ɫɭɤɭɩɧɨɫɬɟɣ
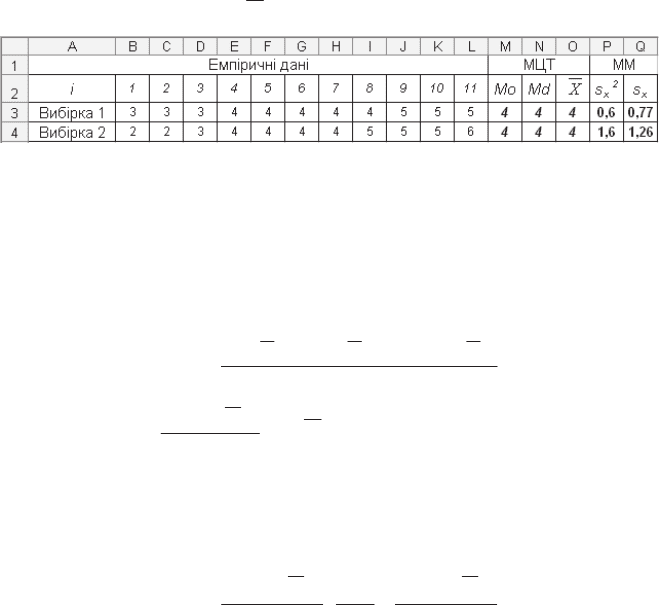
ɦɨɠɧɚ ɩɪɨɞɟɦɨɧɫɬɪɭɜɚɬɢ ɧɚ ɩɪɢɤɥɚɞɿ ɞɜɨɯ ɜɢɛɿɪɨɤ (ɪɢɫ. 2.29), ɹɤɿ ɦɚɸɬɶ
ɪɿɡɧɿ
ɪɨɡɩɨɞɿɥɢ
, ɩɪɨɬɟ ɨɞɧɚɤɨɜɿ (ɿ ɰɟ ɧɟ ɫɤɥɚɞɧɨ ɩɟɪɟɜɿɪɢɬɢ) ɆɐɌ (ɡɧɚɱɟɧɧɹ ɦɨɞɢ
Ɇɨ, ɦɟɞɿɚɧɢ Ɇd ɿ ɫɟɪɟɞɧɶɨɝɨ
X
ɞɨɪɿɜɧɸɸɬɶ 4).
Ɋɢɫ. 2.29. ȼɥɚɫɬɢɜɨɫɬɿ ɆɆ
ɉɪɨɬɟ ɜɢɛɿɪɤɢ ɦɚɸɬɶ ɿɫɬɨɬɧɭ ɪɿɡɧɢɰɸ ɡɧɚɱɟɧɶ ɨɫɧɨɜɧɢɯ ɆɆ: ɞɢɫɩɟɪɫɿɣ
s
2
x
ɿ
ɫɬɚɧɞɚɪɬɧɢɯ ɜɿɞɯɢɥɟɧɶ
s
x
(ɞɢɜ. ɞɜɚ ɨɫɬɚɧɧɿ ɫɬɨɜɩɱɢɤɢ ɪɢɫ. 2.29). Ɇɨɠɧɚ ɜɿɞɡɧɚ-
ɱɢɬɢ ɫɜɨɽɪɿɞɧɭ «ɱɭɬɥɢɜɿɫɬɶ» ɩɨɤɚɡɧɢɤɿɜ ɆɆ ɳɨɞɨ ɜɥɚɫɬɢɜɨɫɬɟɣ ɫɭɤɭɩɧɨɫɬɿ.
Ⱦɢɫɩɟɪɫɿɹ ɜɢɛɿɪɤɢ ɨɛɫɹɝɨɦ
n ɜɢɡɧɚɱɚɽɬɶɫɹ ɹɤ:
1
)()()(
22
2
2
1
2
n
XxXxXx
s
n
x
!
, (2.3)
ɚɛɨ
1
)(
2
2
¦
n
Xx
s
i
x
, ɞɟ
X
– ɫɟɪɟɞɧɽ ɚɪɢɮɦɟɬɢɱɧɟ ɜɢɛɿɪɤɢ.
Ⱦɢɫɩɟɪɫɿɹ ɜɢɛɿɪɤɢ
s
2
x
, ɳɨ ɪɨɡɪɚɯɨɜɚɧɚ ɡɚ ɰɿɽɸ ɮɨɪɦɭɥɨɸ, ɽ ɧɟɡɦɿɳɟɧɨɸ
ɨɰɿɧɤɨɸ ɫɜɨɝɨ ɝɟɧɟɪɚɥɶɧɨɝɨ ɩɚɪɚɦɟɬɪɚ
ı
2
x
ɡɚɜɞɹɤɢ ɜɧɟɫɟɧɧɸ ɩɨɩɪɚɜɤɢ Ȼɟɫɫɟ-
ɥɹ n/(n–1), ɬɨɛɬɨ:
1
)(
1
)(
22
2
¦¦
n
Xx
n
n
n
Xx
s
ii
x
. (2.4)
Ɋɿɡɧɢɰɸ
n–1 ɧɚɡɢɜɚɸɬɶ ɱɢɫɥɨɦ ɫɬɟɩɟɧɿɜ ɜɿɥɶɧɨɫɬɿ k – ɤɿɥɶɤɿɫɬɶ ɨɛ’ɽɤɬɿɜ
ɚɛɨ ɡɧɚɱɟɧɶ ɭ ɫɤɥɚɞɿ ɨɛɦɟɠɟɧɨʀ ɫɬɚɬɢɫɬɢɱɧɨʀ ɫɭɤɭɩɧɨɫɬɿ, ɹɤɿ ɦɨɠɭɬɶ ɜɿɥɶɧɨ
ɜɚɪɿɸɜɚɬɢ. əɤɳɨ ɨɛɦɟɠɟɧɶ ɜɿɥɶɧɨɫɬɿ ɜɚɪɿɚɰɿʀ ɿɫɧɭɽ ɞɟɤɿɥɶɤɚ (
Ȟ), ɬɨ ɱɢɫɥɨ ɫɬɟ-
ɩɟɧɿɜ ɜɿɥɶɧɨɫɬɿ ɞɨɪɿɜɧɸɜɚɬɢɦɟ
k= n–Ȟ (ɞɟ Ȟ – ɝɪɟɰɶɤɚ ɥɿɬɟɪɚ «ɧɸ»).
ɑɢɫɟɥɶɧɢɤ ɮɨɪɦɭɥɢ ɞɢɫɩɟɪɫɿʀ ɦɨɠɧɚ ɩɟɪɟɬɜɨɪɢɬɢ ɭ ɬɚɤɢɣ ɫɩɨɫɿɛ:

40
.2
222
222
)()()()(
2
2
2
2
222
21
22
2
2
1
2
2
2
2
2
2
2
1
2
1
22
2
2
1
2
XnxXnxXx
XXXXxXxXxxxx
XXxxXXxxXXxx
XxXxXxXx
iii
nn
nn
ni
¦¦¦
¦
!!
!
!
Ɍɨɞɿ ɮɨɪɦɭɥɚ ɞɢɫɩɟɪɫɿʀ ɦɚɽ ɬɚɤɢɣ ɜɢɝɥɹɞ:
)(
1
1
2
22
Xnx
n
s
ix
¦
. (2.5)
əɤɳɨ ɞɚɧɿ ɩɪɟɞɫɬɚɜɥɟɧɨ ɪɨɡɩɨɞɿɥɚɦɢ ɱɚɫɬɨɬ, ɞɢɫɩɟɪɫɿɹ ɜɢɡɧɚɱɚɽɬɶɫɹ ɹɤ
¦
22
)(
1
1
Xxf
n
s
iix
, (2.6)
ɞɟ
x
ɿ
– ɜɚɪɿɚɧɬɢ ɧɟɡɝɪɭɩɨɜɚɧɢɯ ɱɚɫɬɨɬ ɚɛɨ ɰɟɧɬɪɚɥɶɧɿ ɡɧɚɱɟɧɧɹ ɤɥɚɫɨɜɢɯ ɿɧ-
ɬɟɪɜɚɥɿɜ ɭ ɪɚɡɿ ɡɝɪɭɩɨɜɚɧɢɯ ɱɚɫɬɨɬ;
f
ɿ
– ɞɢɮɟɪɟɧɰɿɚɥɶɧɿ ɱɚɫɬɨɬɢ,
X
– ɫɟɪɟɞɧɽ.
Ⱦɢɫɩɟɪɫɿɹ ɫɥɭɠɢɬɶ ɦɿɪɨɸ ɨɞɧɨɪɿɞɧɨɫɬɿ ɫɭɤɭɩɧɨɫɬɟɣ ɟɦɩɿɪɢɱɧɢɯ ɞɚɧɢɯ.
ɑɢɦ ɜɢɳɚ ɨɞɧɨɪɿɞɧɿɫɬɶ, ɬɢɦ ɧɢɠɱɟ ɡɧɚɱɟɧɧɹ ɞɢɫɩɟɪɫɿʀ. Ⱦɥɹ ɩɨɜɧɿɫɬɸ ɨɞɧɨɪɿ-
ɞɧɢɯ ɫɭɤɭɩɧɨɫɬɟɣ ɞɢɫɩɟɪɫɿɹ ɞɨɪɿɜɧɸɽ ɧɭɥɸ.
Ⱦɢɫɩɟɪɫɿɹ
ɝɟɧɟɪɚɥɶɧɨʀ ɫɭɤɭɩɧɨɫɬɿ ɨɛɫɹɝɨɦ N ɜɢɡɧɚɱɚɽɬɶɫɹ ɹɤ:
N
xxx
N
x
22
2
2
1
2
)()()(
PPP
V
!
, (2.7)
ɚɛɨ
N
x
i
x
¦
2
2
)(
P
V
, ɞɟ
¦
i
x
N
1
P
– ɫɟɪɟɞɧɽ ɚɪɢɮɦɟɬɢɱɧɟ ɝɟɧɟɪɚɥɶɧɨʀ ɫɭɤɭɩɧɨɫɬɿ.
ɋɬɚɧɞɚɪɬɧɟ ɜɿɞɯɢɥɟɧɧɹ ɜɢɛɿɪɤɢ ɜɢɡɧɚɱɚɽɬɶɫɹ ɹɤ
2
xx
ss . (2.8)
ɋɬɚɧɞɚɪɬɧɟ ɜɿɞɯɢɥɟɧɧɹ ɝɟɧɟɪɚɥɶɧɨʀ ɫɭɤɭɩɧɨɫɬɿ
2
xx
VV
. (2.9)
Ʉɨɟɮɿɰɿɽɧɬ ɜɚɪɿɚɰɿʀ
V
x
ɜɢɤɨɪɢɫɬɨɜɭɽɬɶɫɹ ɭ ɪɚɡɿ ɩɨɪɿɜɧɹɥɶɧɨʀ ɨɰɿɧɤɢ ɪɿɡ-
ɧɨɹɤɿɫɧɢɯ ɫɟɪɟɞɧɿɯ ɜɟɥɢɱɢɧ ɿ ɜɢɡɧɚɱɚɽɬɶɫɹ (ɭ ɬɨɦɭ ɱɢɫɥɿ ɭ %) ɹɤ ɜɿɞɧɨɲɟɧɧɹ
ɫɬɚɧɞɚɪɬɧɨɝɨ ɜɿɞɯɢɥɟɧɧɹ ɞɨ ɫɟɪɟɞɧɶɨɝɨ ɚɪɢɮɦɟɬɢɱɧɨɝɨ:
XsV
xx
/
·100% . (2.10)
Ⱥɫɢɦɟɬɪɿɹ A
x
ɯɚɪɚɤɬɟɪɢɡɭɽ ɫɬɭɩɿɧɶ ɧɟɫɢɦɟɬɪɢɱɧɨɫɬɿ ɪɨɡɩɨɞɿɥɭ ɜɿɞɧɨɫɧɨ
ɣɨɝɨ ɫɟɪɟɞɧɶɨɝɨ. ɉɨɡɢɬɢɜɧɚ ɚɫɢɦɟɬɪɿɹ ɜɤɚɡɭɽ ɧɚ ɜɿɞɯɢɥɟɧɧɹ ɜɟɪɲɢɧɢ ɪɨɡɩɨ-
ɞɿɥɭ ɜ ɛɿɤ ɜɿɞ'ɽɦɧɢɯ ɡɧɚɱɟɧɶ, ɧɟɝɚɬɢɜɧɚ – ɭ ɛɿɤ ɞɨɞɚɬɧɢɯ.
