Рудакова Л.И., Соколова Е.Ю. Практический курс физики. Волновая оптика
Подождите немного. Документ загружается.


41
,
(
)
b
a
k += 127,7
,
min
k
=8.
8
min
== kk
,
1,0=
b
a
;
b 10
=
.
2.4. , ,
S
P
,
O
S
P
.
r
P
.
P
?
.
P
:
...
222222
...
222
7
6
55
4
321
54
321
++−++−+−=
=++−+−=
21
≈
2
11 +−
+
≈
mm
m
AA
,
;
0
≈
A
.
P
.
( .2.14).
3
,
.
3
(
3
′
).
, ,
P
,
0
′
.
P
0
03
≈
′
+
′
=
.
. 2.13
. 2.14

42
2.5.
P
,
.
P
1
I
.
,
P
4
1
I
.
. . 2.15
1
:
01
2=
,
0
-
:
4
I
I
1
0
=
. ,
0
=
.
3
π
ϕ
=∆
.
r
,
P
,
,
3
π
ϕ
=∆
.
. 2.16:
( )
L−=∆
ρ
λ
π
ϕ
2
( )
6
λ
ρ
=− L
.
. 2.16
(
)
(
)
2
2
2
2
xLxRR +−=−−
ρ
;
22
22 LLxRx −−=
ρ
;
( )
(
)
(
)
( )
LR
LL
LR
L
x
+
+−
=
+
−
=
22
22
ρρρ
(
)
L−
ρ
<λ,
LL 2
≈
+
ρ
;
(
)
;2
2
2
22
xRxxRRr −=−−=
2
x
,
Rxr 2
2
=
.
x
:
(
)
L
R
LRL
r
+
−
=
ρ
2
2
,
, ,
. 2.15
. 2.16

43
LR
LR
r
+
=
λ
1
,
(
)
2
1
2
2
r
L
r
λ
ρ
−
=
.
( )
6
λ
ρ
=− L
,
3
2
1
2
r
r =
;
3
1
r
r =
.
1,73 .
2.6.
0
I
λ
r
.
,
b
b(
>>
r
).
.
∞
→
r
.
P
,
,
0
I
;
0
A
. ( .2.17).
,
,
.
.
2.18.
0
.
r
.
B
O
( . 2.17)
( )
b−=∆
ρ
λ
π
ϕ
2
;
222
rb =−
ρ
;
b
r
b
+
=−
ρ
ρ
2
.
. 2.17
. 2.18

44
r
<<
b
bb 2
≈
+
ρ
b
r
2
2
2
λ
π
ϕ
=∆
,
r
, ,
A
. . 2.18 :
2
sin2
0
ϕ
∆
= AA
;
b
r
AA
λ
π
2
sin2
2
0
=
;
=
b
r
II
λ
π
2
sin4
2
0
.
2.7.
0
I
, ,
. 2.19. ,
, .
P
,
O
.
r
,
b
, λ.
.
P
,
,
.
r
r
.
( . 2.20)
(
1
)
(
2
):
21
+=
.
2.6,
1
:
b
r
λ
π
2
sin2
2
01
=
.
2
A
,
. 2.19
. 2.20

45
P
,
0
(
0
I
),
(
1
)
(
3
)
310
+=
.
03
=
( . . 2.20).
2
,
, ,
3
,
2
2
03
2
==
.
α
os
21
2
1
2
2
2
2−+=
,
2
ϕ
π
α
∆
−
=
.
2.6
b
r
λ
π
ϕ
2
=∆
,
2
sin
22
cos
ϕϕπ
∆
=
∆
−
,
)
2
(sin2
2
2
2
sin4
4
2
2
0
0
2
22
0
2
0
2
b
r
A
A
b
r
A
A
A
λ
π
λ
π
⋅−+=
+=
b
r
II
λ
π
2
sin2
4
1
2
2
0
.
2.8. λ
,
.
?
n
.
.
( . 2.21).
0
.
: ,
. 2.21

46
.
1
.
.
2
.
021
=+
. ,
.
(
)
1−nh
,
h
-
.
:
λ
π
ϕ
2
=∆
(
)
1−nh
.
1
ϕ
∆
.
12
+=
,
1
2
.
π
π
ϕ
2
4
5
+=∆
,
,...2,1,0
=
,
mnh
π
π
λ
π
2
4
5
)1(
2
+=−
.
(
)
)1(2
4
5
2
−
+
=
n
m
h
λ
.
2.9.
(2.7)
.
.
b
.
,
( .
2.22).
ϕ .
( . 2.6).
. 2.22
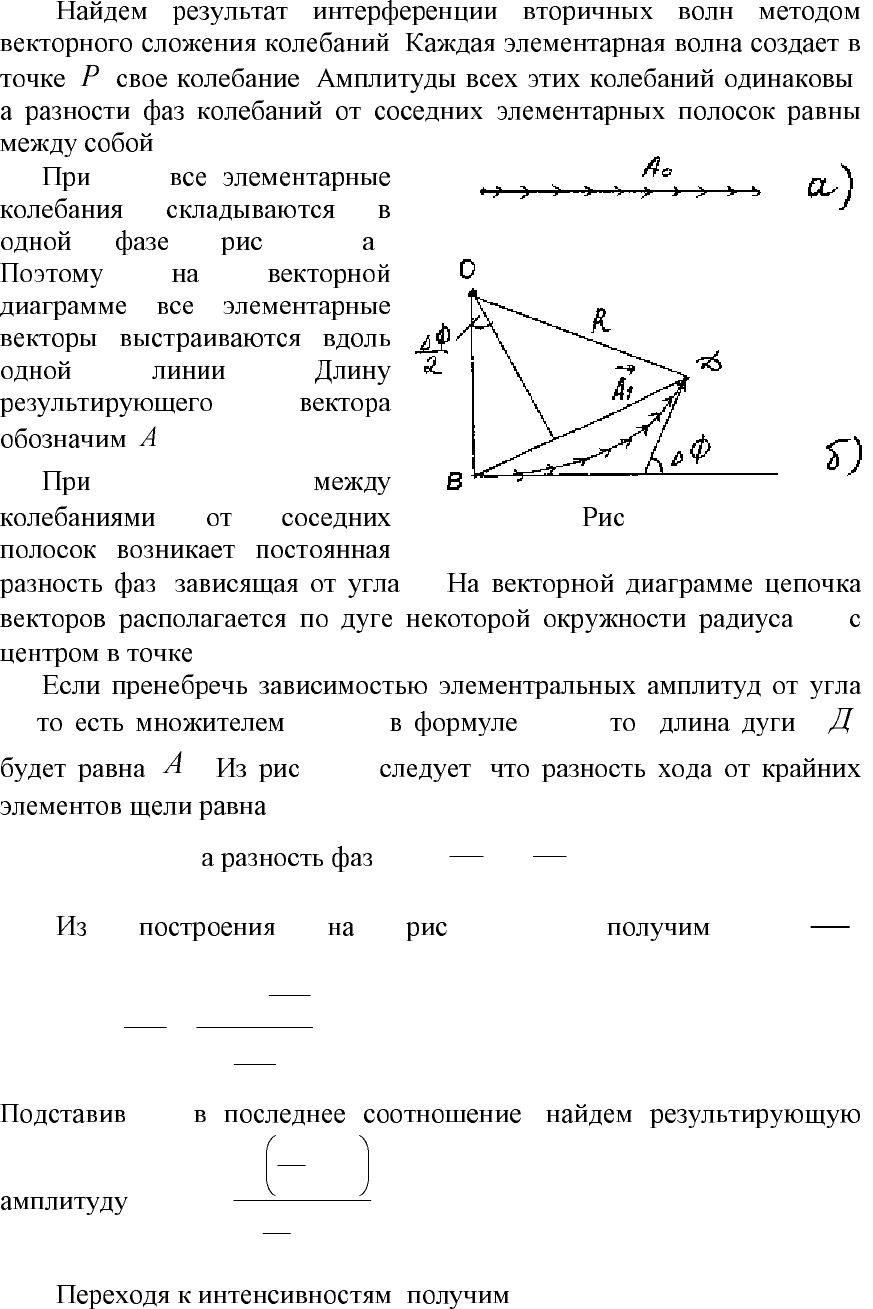
47
.
. ,
.
ϕ=0
( . 2.23 ).
.
0
.
0
≠
ϕ
, ϕ.
R
Ο.
ϕ (
)(
ϕ
k
(2.1)),
B
0
. . 2.22 ,
ϕ
sinb
=
∆
,
ϕ
λ
π
λ
π
sin
22
b=∆=∆Φ
.
. 2.23
∆Φ
=
0
A
R
;
2
2
sin
2
sin2
0
∆Φ
∆Φ
=
∆Φ
=
A
RA
.
∆Φ
,
ϕ
λ
π
ϕ
λ
π
sin
sinsin
0
a
a
AA =
.
,
. 2.23

48
2
2
0
sin
sinsin
=
ϕ
λ
π
ϕ
λ
π
a
a
II
,
0
I
- (
ϕ
=0).
,
,
, ( . 2.23).
2
π
∆Φ
=
λ
=
∆
,
...
,
2
,
1
±
±
=
2.10.
5,0
=
λ
b 10
=
0
0
30=
θ
.
,
.
. ,
ϕ.
,
( ).
. ,
0
sinsin
θ
ϕ
bb
−
=
−
=
∆
.
0
θ
ϕ
=
, ,
( ), 0; ,
0
θ
ϕ
=
.
( )
( 2.9):
λ
±
=
∆
.
0
sinsin
θ
λ
ϕ
+=
b
;
55,0sin
=
ϕ
;
0
37,33=
ϕ
.
. 2.24

49
( ) :
b
λ
θϕ
−=
0
sinsin
;
45,0sin
=
ϕ
;
0
74,26=
ϕ
.
2.11. ,
,
.
.
λ
ϕ
md
=
sin
. (2.12)
:
λ
ϕ
kb
=
sin
; (2.11)
N
kd
λ
ϕ
′
=sin
. (2.13)
1
−
N ,
(2.13).
.
3=
b
d
, (2.12)
λ
ϕ
mb
=
sin3
;
λϕ
3
sin
m
b =
.
m
,
, (2.11),
. , 3- , 6- , 9- … .
, . 2.25.
2.12.
600
=
λ
d 0,3
=
,
20000
=
N
.
.
. 2.25

50
. ,
m- ( . (2.13));
N
md
λ
λϕ
−=
1
sin
,
N
md
λ
λϕ
+=
2
sin
.
( )
N
d
λ
ϕϕ
2
sinsin
12
=−
;
Nd
2
2
cos
2
sin2
1212
λ
ϕ
ϕ
ϕ
ϕ
=
+
−
.
N
(
)
12
ϕϕδϕ
−=
,
ϕ
ϕϕ
=
+
2
21
(
δϕ
m- ;
ϕ
- ,
m- );
dN
os
λ
ϕδϕ
2
1
=
, ,
λ
ϕ
md
=
sin
, :
5
2
2
2
101,1
1)
2
(
1
4
1
2
−
×=
−
=
−
=
λ
λ
λ
δϕ
d
N
d
dN
.
2.13.
l 5,6
=
, 200 .
8,670
=
λ
,
,
015,0
=
δλ
.
:
) ;
) ,
8,670
=
λ
.
.
mN=
δλ
λ
.
n
l
N
⋅
=
,
n
- .
,
.44,3
20065015,0
8,670
=
⋅⋅
==
ln
m
δλ
λ
, :
4
=
m
.
min
δλ
, ,
,
