Рудакова Л.И., Соколова Е.Ю. Практический курс физики. Волновая оптика
Подождите немного. Документ загружается.


31
,
P
,
(
)
ϕ
k
(c . – (2.1));
, m-
m:
1
>
2
>
3
>…
2
11 +−
+
=
. ,
,
...
22222
...
5
4
33
2
11
4321
++−++−+=+−+−=
,
2
1
=
- ,
.
,
.
,
,
λ
.
,
( . 2.4).
,
. , ,
, ,
, .
. . 2.5 )
– 1- ; ) 1- 2- ; ) 1- , 2- 3-
, ) 1- , ; )
1- ; ) – . . 5.5.
.
.2.5 :
, ,
. 2.4

32
(
)
01
2=
,
.
. ,
.
.
, ,
, ( ).
.
.
.
0
,
.
, ,
,
, .
.
.
,
,
.
.
, ,
, .
.
∞
→
R
, (2.3)
. 2.5

33
Lmr
m
λ
=
(2.4)
L
r
m
λ
2
=
(2.5)
,
L
. ,
,
. ,
.
.
.
.
,
.
,
.
, ,
,
,
.
,
L
r
λ
2
=
.
L
r
λ
2
−<<
−
−>>
1
1
1
(2.6)
(2.6) ,
. ,
b
L
b
λ
2
.
.
b
.
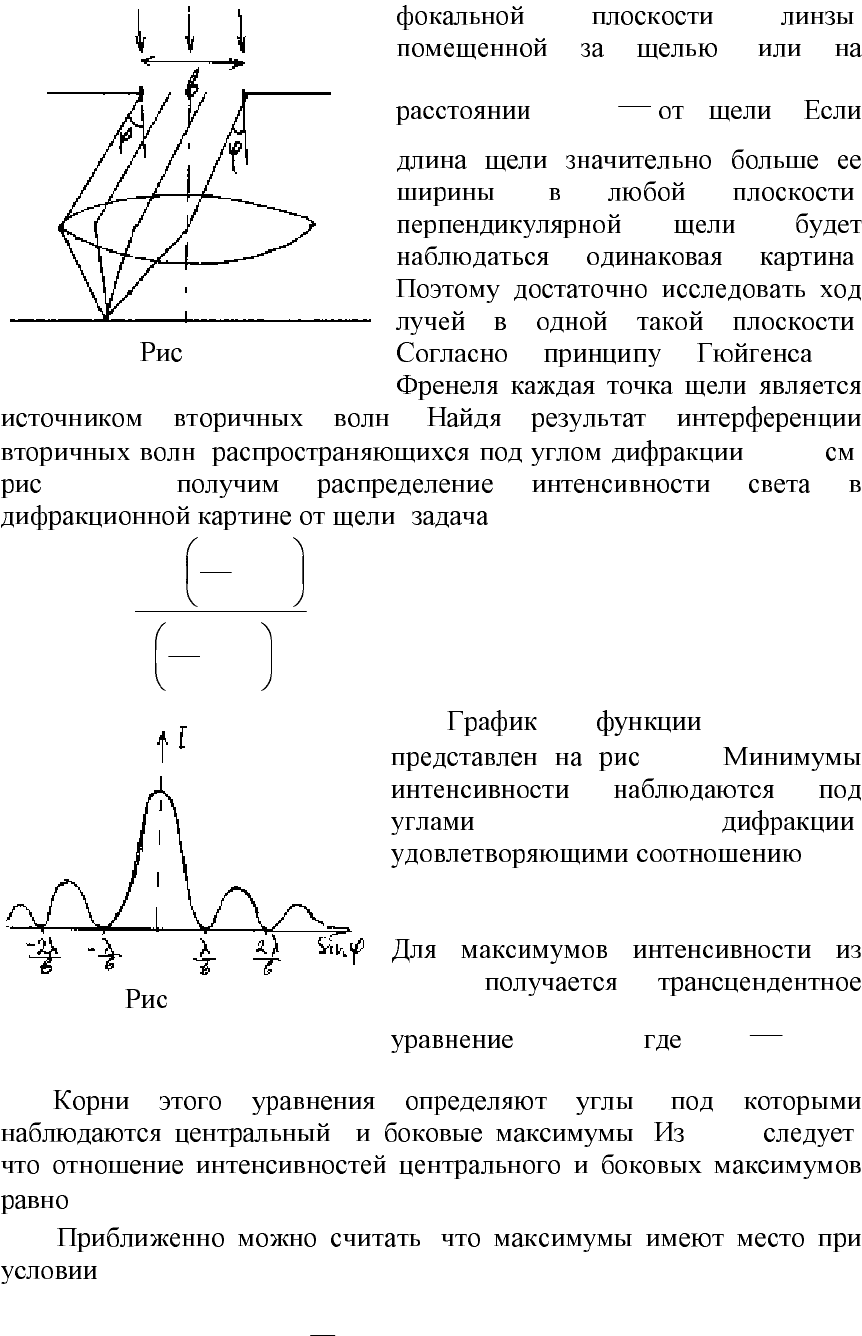
34
,
,
L
>>
λ
2
b
.
, ,
,
.
.
–
.
,
ϕ
( .
. 2.6),
( 2.9):
2
2
0
sin
sinsin
=
ϕ
λ
π
ϕ
λ
π
b
b
II
. (2.7)
(
)
ϕ
sinI
. 2.7.
,
λ
ϕ
mb
=
sin
,
,...
2
,
1
m
±
±
=
(2.8)
(2.7)
α
α
=
tg
,
ϕ
λ
π
α
sin
b
=
.
,
. (2.7) ,
.016,0:045,0:1...::
210
=III
,
( )
2
12sin
λ
ϕ
+±= mb
. (2.9)
. 2.6
. 2.7
35
.
( )
.
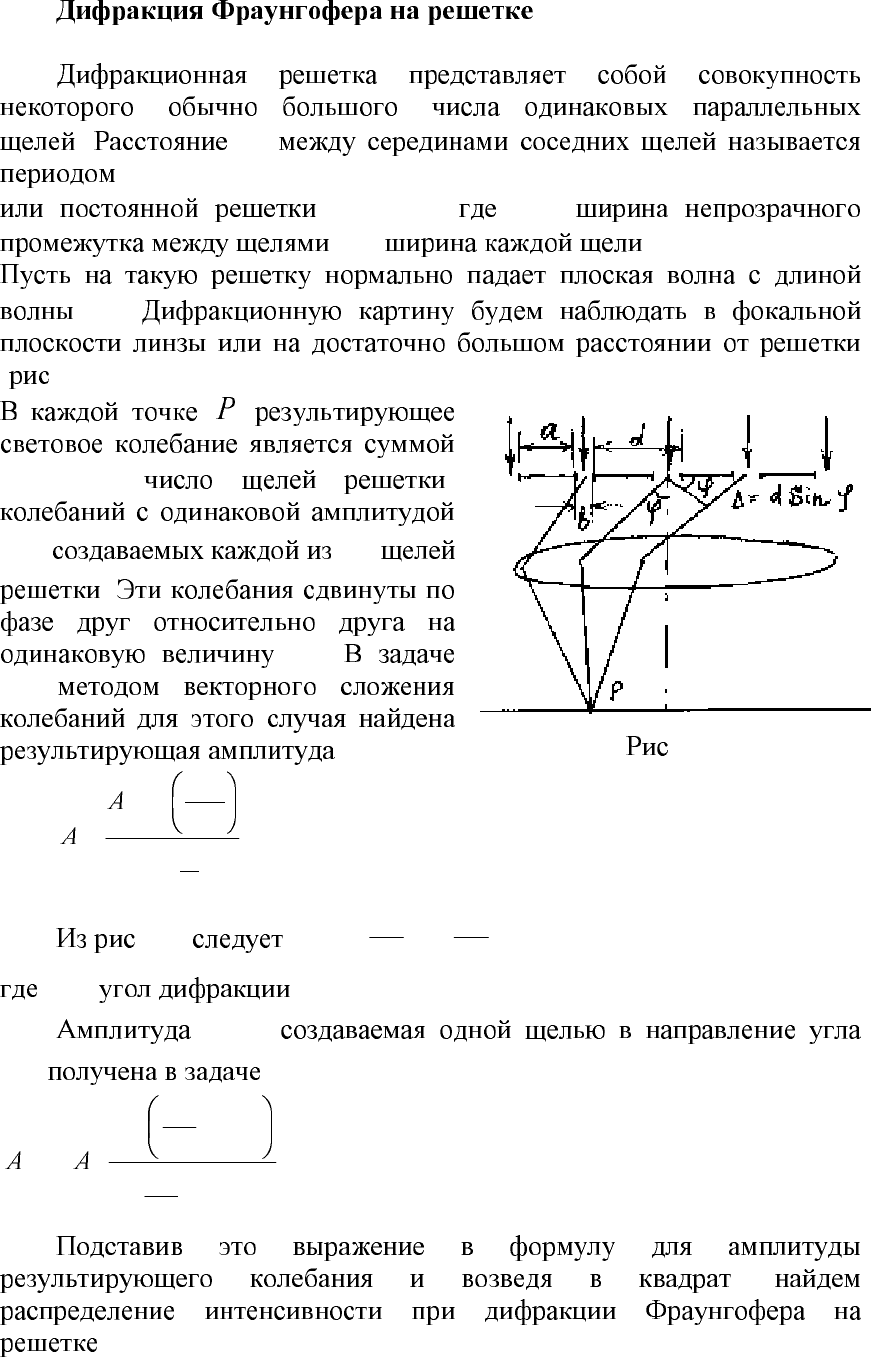
d
,
:
bad
+
=
,
a
-
,
b
- .
λ
.
( . 2.8.).
N
(
N
- )
ϕ
A
,
N
.
α
.
1.3
2
sin
2
sin
α
α
ϕ
=
N
.
. 2.8
ϕ
λ
π
λ
π
α
sin
22
d=∆=
,
ϕ
- .
ϕ
A
,
ϕ
, (2.9) :
ϕ
λ
π
ϕ
λ
π
ϕ
sin
sinsin
0
b
b
=
,
,
.
. 2.8

36
2
2
0
sinsin
sinsin
sin
sinsin
=
ϕ
λ
π
ϕ
λ
π
ϕ
λ
π
ϕ
λ
π
d
dN
b
b
II
(2.10)
(
)
ϕ
sinI
. 2.9.
,
. 2.9
.
.
, (2.8),
ϕ
A
.
λ
ϕ
kb
=
sin
,
...
,
2
,
1
k
±
±
=
(2.11)
(2.10)
λ
ϕ
md
=
sin
,
,...
2
,
1
,
0
m
±
±
=
(2.12)
,
m
-
, . (2.12)
,
ϕ
NA=
,
,
I
~
2
N
.
(2.10)
λ
N
k
d
′
=sin
,
(
)
(
)
,...
1N,1N...,,2,1k
+
±
−
±
±
±
±
=
′
(2.13)
.
1
−
N
.
.
N
.
2
−
N
.
( .
2.12),
N
,
N
,
. (2.12) ,
. 2.9

37
λ
.
, ,
,
.
,
.
R
.
,
:
λ
ϕ
d
d
=
. (2.14)
(2.12)
λ
ϕ
ϕ
mddd
=
cos
,
ϕ
cosd
=
(2.15)
δλ
λ
=R
(2.16)
δλ
- ,
.
( ),
(
) ( . 2.10).
.
,
δλ
,
.
(2.12) (2.13)
( )
λδλλ
+=+
N
1
,
mNR
=
(2.17)
. 2.10
38
.
, .
d
10
10
−
≈
.
,
d
>λ (c . -
(2.12)).
d
10
10
−
≈
.
– .
.
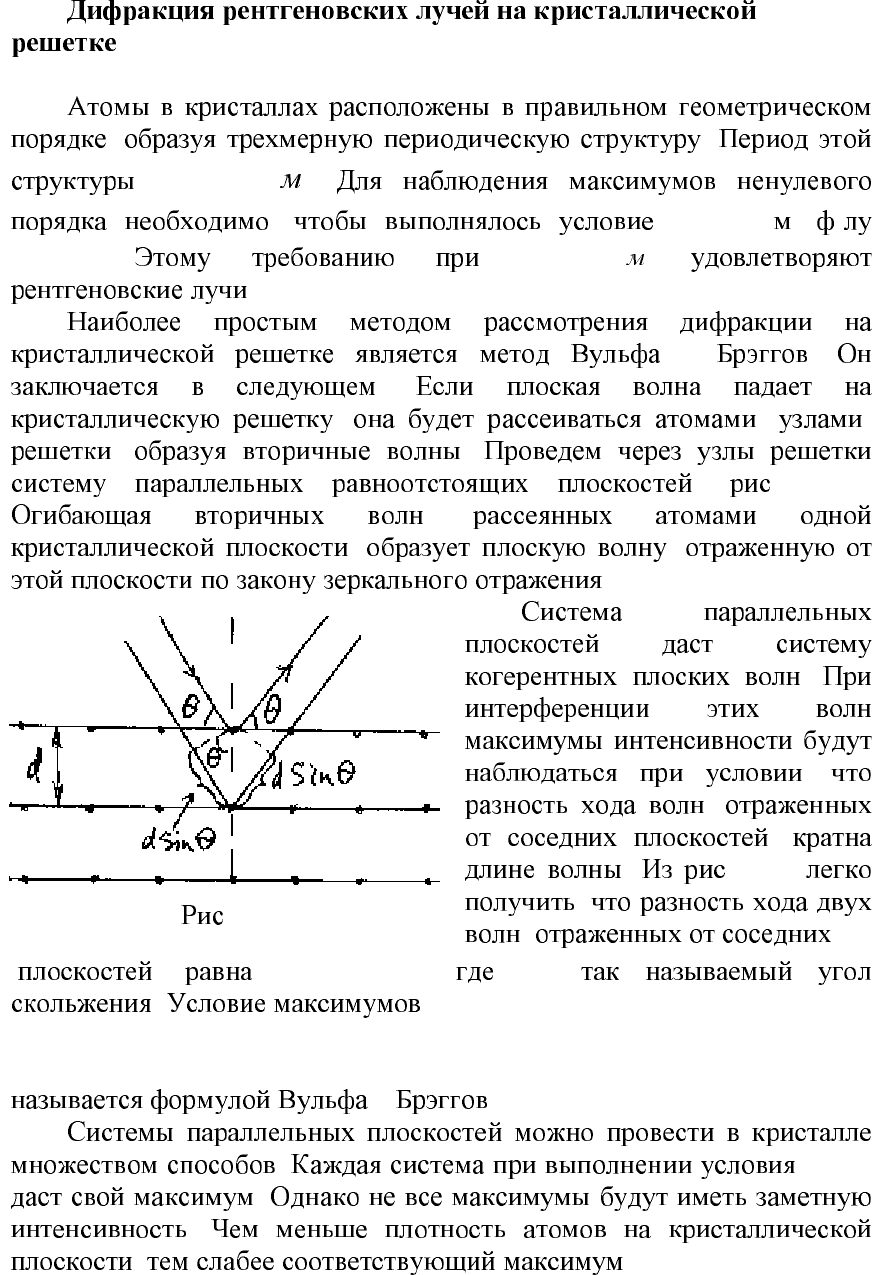
, ( )
, .
( . 2.11).
,
, ,
.
.
,
,
,
. . 2.11
,
,
,
θ
sin2d
=
∆
,
θ
-
.
λ
θ
md
=
sin2
,
...
,
2
,
1
m
±
±
=
(2.18)
– .
. (5.18)
.
.
, .
. 2.11
39
.
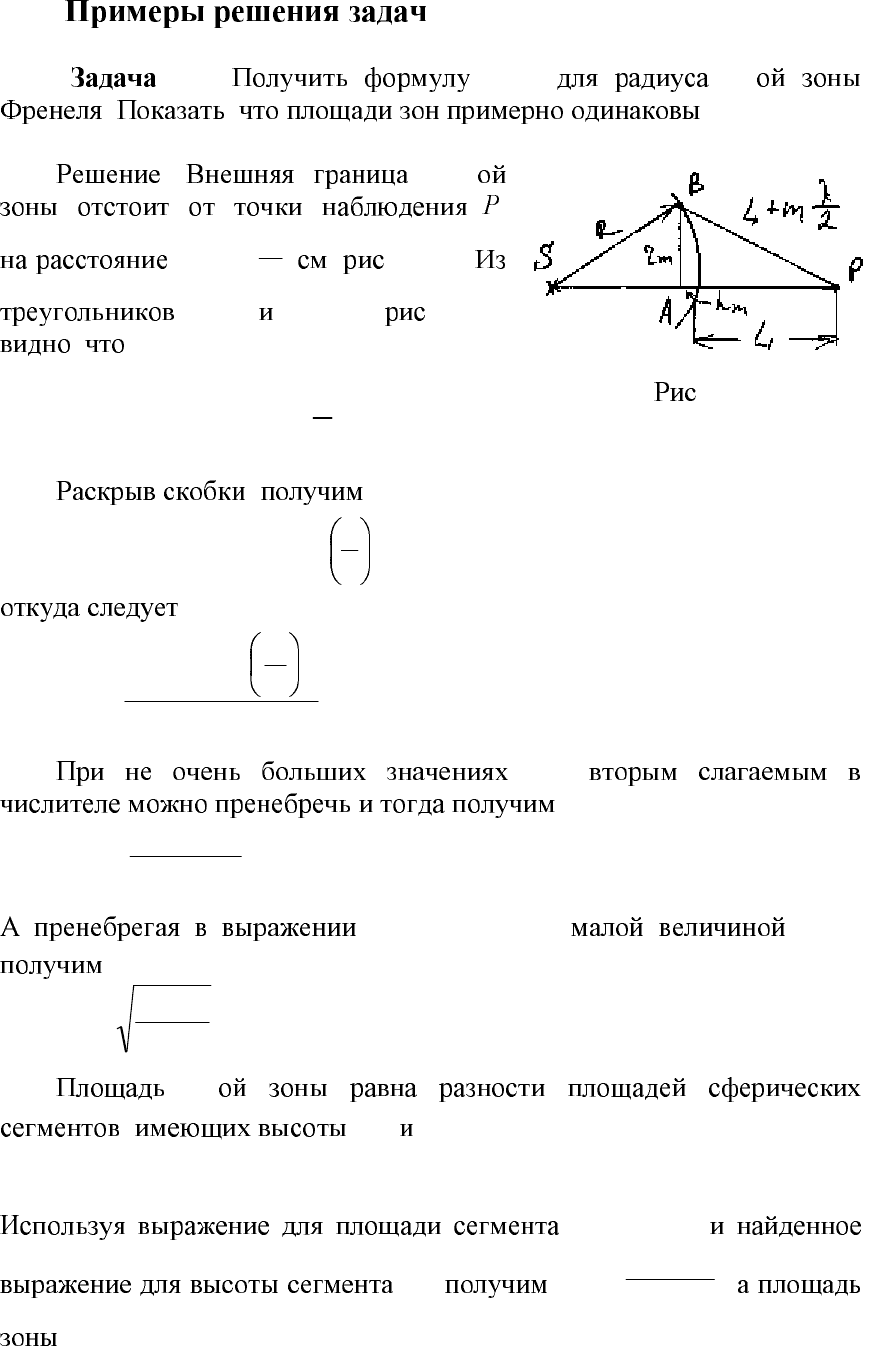
2.1. (2.3) m-
. , .
. m-
2
λ
mL +
( . . 2.12).
SAB
ABP
. 2.12
,
,
2
mm
2
22
mm
2
m
hLh2
2
mmLhRh2r −−+=−=
λ
λ
,
( )
LR
mmL
h
m
+
+
=
2
2
2
2
λ
λ
m
( )
LR
mL
h
m
+
=
2
λ
.
22
2
mmm
hRhr −=
2
m
h
,
LR
RLm
r
m
+
=
λ
.
m-
,
m
h
1−m
h
:
1−
−=∆
mmm
SSS
.
RhS
π
2
=
h
,
)( LR
mRL
S
m
+
=
λ
π
,
22222
)()
2
()(
mmm
hLmLhRRr +−+=−−=
λ
. 2.12

40
L
R
RL
SSS
mm
+
=−=∆
−
λ
π
1
.
,
m
m
, .
2.2.
r 2
=
5,0
=
λ
. ,
b 1
=
,
.
- ?
?
?
?
. , ,
m- (2.4)
bmr
m
λ
=
,
b
r
m
λ
2
=
.
,
8
=
m
. 8
.
.
,
( . 2.5 ).
r
b 8
2
1
==
λ
.
2
=
m
( . 2.5, ),
r
b 4
2
2
2
==
λ
.
2.3.
(
)
550=
λ
00,1
=
r 00,2
=
.
k
.
k
?
(
k
) ?
. (2.3)
)1(
2
b
a
a
r
k +=
λ
.
