Рудакова Л.И., Соколова Е.Ю. Практический курс физики. Волновая оптика
Подождите немного. Документ загружается.

21
1.9. ,
α<<1 ,
. ,
=
∆
λ/α, λ - .
.
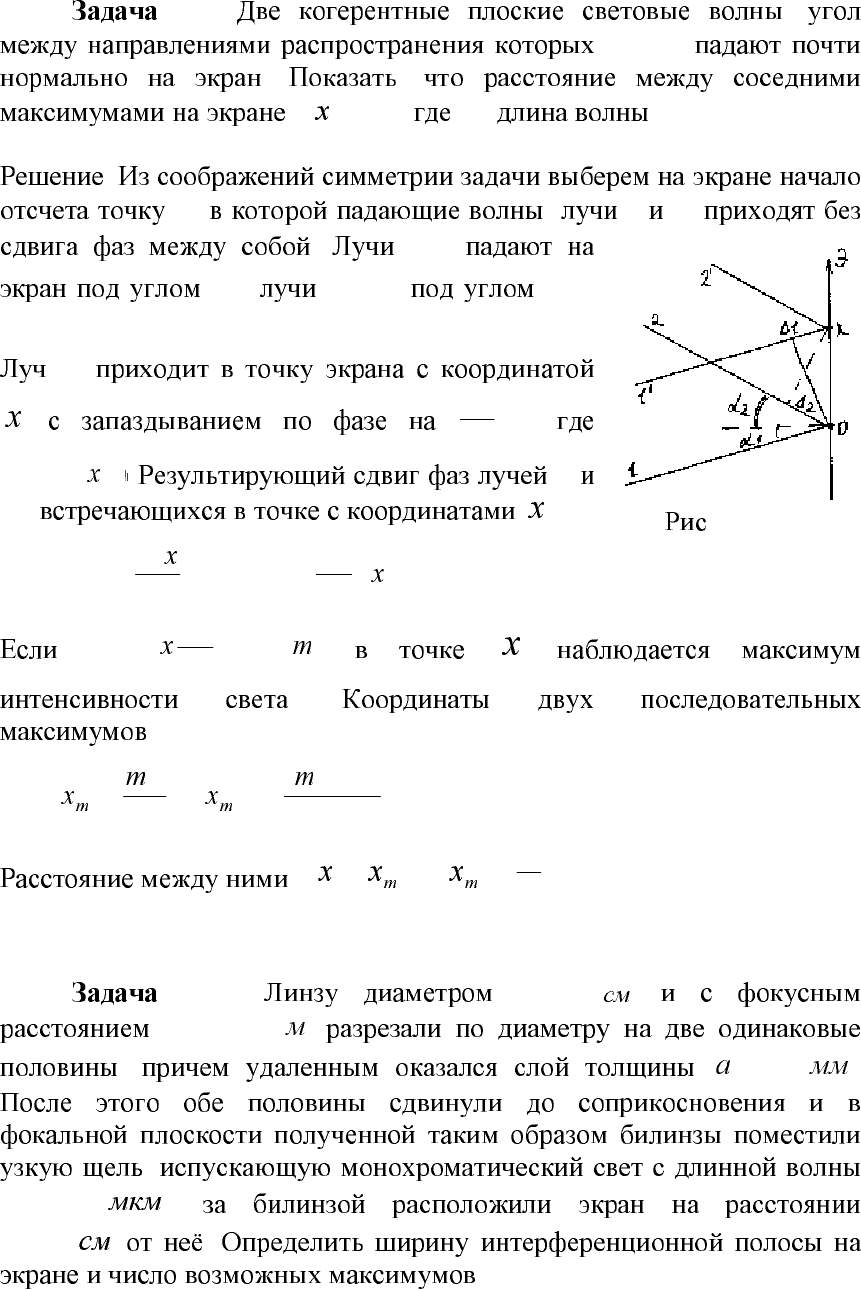
Ο, ( 1 2)
.
1,1
′
1
α
,
2,2
′
-
:
2
α
21
,
α
α
<<
1
;
21
α
α
α
+
=
.
1
′
1
2
∆
λ
π
,
11
α
=∆
.
. 4.13.
1
′
2
′
, ,
( )
α
λ
π
αα
λ
π
ϕ
22
21
=+=∆
.
πα
λ
π
ϕ
2
2
==∆
,
.
:
α
λ
=
,
(
)
α
λ
1
1
+
=
+
.
α
λ
=−=∆
+1
1.10.
0
.
5
D
=
cf 0,25
=
,
00,1
=
.
,
60,0
=
λ
,
b 50
=
.
.
. 1.18

22
. ,
( . 1.19). - ,
,
S
2
.
,
,
2
α
,
1
α
.
, ,
f
2
1
==
αα
.
1.9
a
f
15,0===∆
λ
α
λ
.
.
( . . 1.20), . .
. 1
II.
f
ab
b ==∆Χ
α
. 1.19
. 1.20

23
.13
2
2
===
∆
∆Χ
=
λ
λ
f
ba
a
f
f
ab
x
N
1.11. (1.17)
. ,
d
, 1 2
.
.
,
,
1 2 . (1.11)
1 2
(
)
.2
11
nnABnBPABn
−
=
−
+
=
∆
n
- ,
1
n
-
.
. 1.21
β
cos
d
=
,
,sin2sin
α
β
α
dtg
=
=
α
- ,
β
- . ,
1
sin
sin
n
n
=
β
α
,
βββ
β
cos2sin2
cos
2
1
1
dn
n
n
dtgn
d
n =−=∆
1.12.
33,1
=
n
,
64,0
1
=
λ
,
40,0
2
=
λ
.
0
30=
α
. 1.21

24
.
d
n
(1.17):
β
cos2dn
=
∆
,
β
- .
∆
α
.
;
sin
sin
n=
β
α
n
α
β
sin
sin =
;
.
sin
1cos
2
2
n
α
β
−=
α
22
sin2 −=∆ nd
1
λ
:
11
1
2
λ
λ
m=+∆
2
1
11
λ
λ
−=∆ m
,
2
λ
:
( )
2
12
2
2
2
2
λ
λ
+=+∆ m
22
λ
m=∆
.
,
22
1
11
2
λ
λ
λ
mm =−
;
2
1
1
2
2
12
m
m −
=
λ
λ
2
λ
1
λ
:
.
8
5
64,0
40,0
2
12
2
1
==
−
m
m
,
1
m
2
m
,
:
,3
1
=
m
4
2
=m
.
min
d
, ,
;2
22
min
4sin2
λα
=−nd
.
sin
2
22
2
min
α
λ
−
=
n
d
, :
.65,0
min
d
=

25
1.13.
6,0
=
λ
,
.
R 10
=
.
. ,
r 8.3
=
.
.
.
( . 1.22).
: 1,
,
2,
.
R
, 1 2
. ( .
).
1 2
d
( . (1.17)),
.
(1.19),
1cos
=
β
,
2
λ
( 2
, ,
,
π
2
; 1
)
λ
mdn
=
2
.
d
r
.
AOB
222222
2)( dRdRrdRrR +−+=−+=
.
2
d
,
Rdr 2
2
=
.
n
2
m
d
λ
=
,
. 1.22

26
2
r
mR
n
λ
=
.
25,1n)3m(
=
=
.
1.14. -
1
R
,
-
2
R
>
1
R
.
λ.
m
−
.
.
, –
.
(
)
(1.18) (
1
=
n
,
1cos
=
β
)
2
2
λ
+=∆ d
,
d
- .
(
ρ
)
.
−
- :
2
)12(
2
2
λ
λ
+=+ md
λ
md
=
2
.
d
1
R
,
2
R
ρ
.
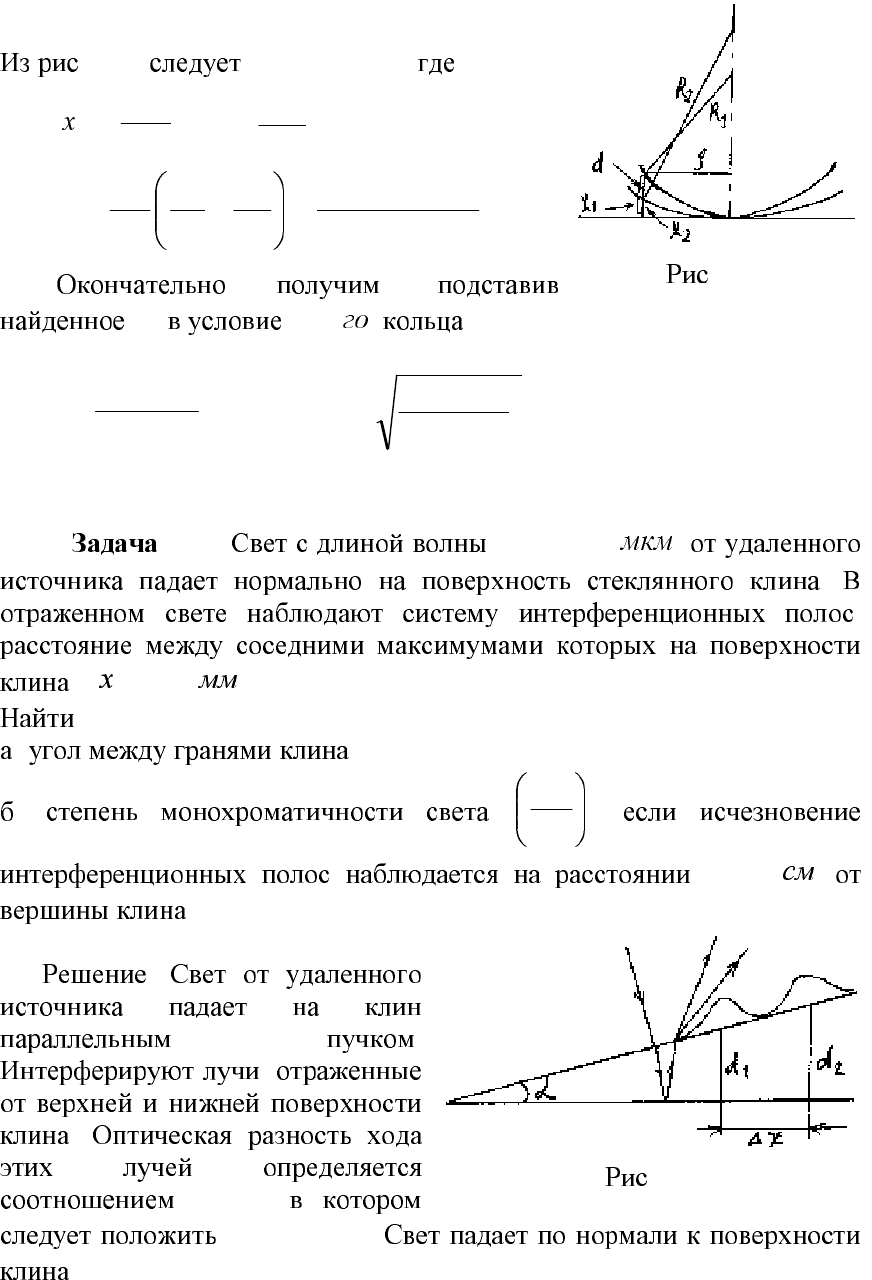
. 1.24 :
;)(
222
hRR −+=
ρ
22
20 hRh+−=
ρ
.
2
h
Rh
:
. 4.23.
. 1.23
. 1.24
27
Rh2
2
=
ρ
.
. 1.25 :
21
xxd −=
,
1
2
1
2R
ρ
=
;
2
2
2
2R
x
ρ
=
;
.
RR2
)RR(
R
1
R
1
2
d
21
12
2
21
2
−
=−=
ρρ
,
d
m
−
:
λρ
m
RR
RR
=
−
21
12
2
)(
;
.
12
21
RR
RRm
−
=
λ
ρ
1.15.
55,0
0
=
λ
.
,
21,0
=
∆
.
:
) ;
)
∆
0
λ
λ
,
l 5,1
≈
.
.
.
,
.
(1.18),
1cos
=
β
. (
):
. 1.25
. 1.26

28
2
2
0
λ
+=∆ dn
.
d
- .
,
.
,
.
:
0
0
1
2
2
λ
λ
mnd =+
;
0
0
2
)1(
2
2
λ
λ
+=+ mnd
.
,
(
)
012
2
λ
=− ndd
.
α
xdd
∆
=
−
12
xn
∆
=
2
0
λ
α
.
,
5,1
=
n
.
.3
′
=
α
1.7 ,
:
λ
λ
∆
≈
0
1
N
;
xNl ∆=
1
.
:
l
x
∆
≈
∆
0
λ
λ
.
, :
.014,0
0
≈
∆
λ
λ

29
II. .
- . .
,
, , ,
. .
:
,
.
– ,
.
, ,
. .
.
S
P
.
Σ ( .2.1).
σ
d
,
.
P
),cos()(
0
ψ
σ
ϕ
+−= krwt
r
da
kdE
(2.1)
r
-
σ
d
P
,
0
a
,
σ
d
,
ψ
- .
P
)(
0
ϕ
σ
k
r
d
ϕ
σ
d
σ
d
P
.
)(
ϕ
k
ϕ
.
ϕ
=0
k
;
2
π
ϕ
=
k
=0.
. 2.1

30
,
Σ:
( )
.cos)(
0
ψ
σ
ϕ
+−= krwt
r
da
kE
(2.2)
Σ ,
.
,
Σ ,
,
, .
(2.2) .
,
SP
,
P
( .2.2).
Σ ,
P
2
λ
:
2
1
λ
+=
;
...
2
12
λ
+=
.
,
,
.
R
,
LOP
=
( .2.3) . m- ( .
2.1)
LR
RLm
r
m
+
=
λ
(2.3)
. 2.2
. 2.3
