Рудакова Л.И., Соколова Е.Ю. Практический курс физики. Волновая оптика
Подождите немного. Документ загружается.


61
( )
01
1
2
1
II
η
−=
.
0
I
- , 1-
;
2
1
,
; η -
.
(
)
αη
2
12
cos1−= II
,
α - .
( )
( )
25,4
cos1
2
1
1
I
I
cosI1
2
1
I
2
2
2
0
2
0
2
2
=
−
=
−=
αη
αη
.
3.2.
.
4
=
,
0
75=
ϕ
,
. .
.
.
:
01
II
2
1
I +=
.
0
75=
ϕ
( )
ϕ
2
02
osII
2
1
I +=
.
21
nII
=
.

62
(1) (2) (3),
( )
ϕ
2
0
cosn1
I1
2
1
I
−
−
= .
P
I
,
:
%67%100
II
I
0
=⋅
+
=
.
3.3. ,
, .
, ,
ϕ
k 3
=
.
k
I
,
I
.
. ,
, ,
, , ,
2 , ,
kmax
I
2
1
II +=
.
,
, ,
, , -
k
I
2
1
:
kmin
I
2
1
I =
.
k
k
I
2
1
k
k
I
2
1
I
=
+

63
.4
2
19
2
1k
I
I
k
2
1
2
1
I
I
.Ik
2
1
I
2
1
I
2
k
2
k
k
2
k
=
−
=
−
=
=+
=+
3.4.
P
.
,
.
I
P
,
0
I
.
? ,
.
. ,
,
1
2
.
0
. , ,
01
2=
,
02
2=
.
, ,
1-
, ,
.
,
1
2
2
π
.
jwtsinE2iwtcos2jEi
0.021
⋅⋅⋅+⋅⋅=⋅+⋅= .
P
,
I
~
2
2
2E ⋅=
0
I2I =
.

64
3.5.
4
λ
,
.
0
I
.
, .
0
90
.
I
?
.
1
,
2
,
.
0
-
.
,
,
0
90
,
2
π
1
.
)wtcos(EEwtcosEwtsinE
wtcosE)
2
wtcos(
2
2
2
121
21
ϕ
π
++=+=
=++=
,
02
EE =
,
01
2EE =
.
0
2
0
2
0
2
2
2
1
54 EEEEEE =+=+=
.
. .
E
,
0
5II =
.
3.6. ,
, ,
. .
, : )

65
,
α ; )
, ,
.
. ) ,
wt
cos
=
wtay sin
=
.
,
δ,
wt
cos
=
)sin(
δ
+
=
wtay
.
.sincossin
cos)sinsin(cos
)sin(sincoscos
wta
wta
wtawta
⋅⋅⋅+
+⋅+=
=
+
⋅
⋅
+
⋅
⋅
=
δα
δαα
δ
α
α
ξ
(
)
(
)
[
]
(
)
.sin2sin1acossinsinsincosaI
2
22
2
δαδαδαα
⋅+=⋅+⋅+=
) δ
,
0
2
cos
=
α
, . .
.
4
3
,
4
π
π
α
=
δ
sin
>0, .
δ
sin
<0 - .
3.7.
,
0
30=
α
.
,
2
λ
. β
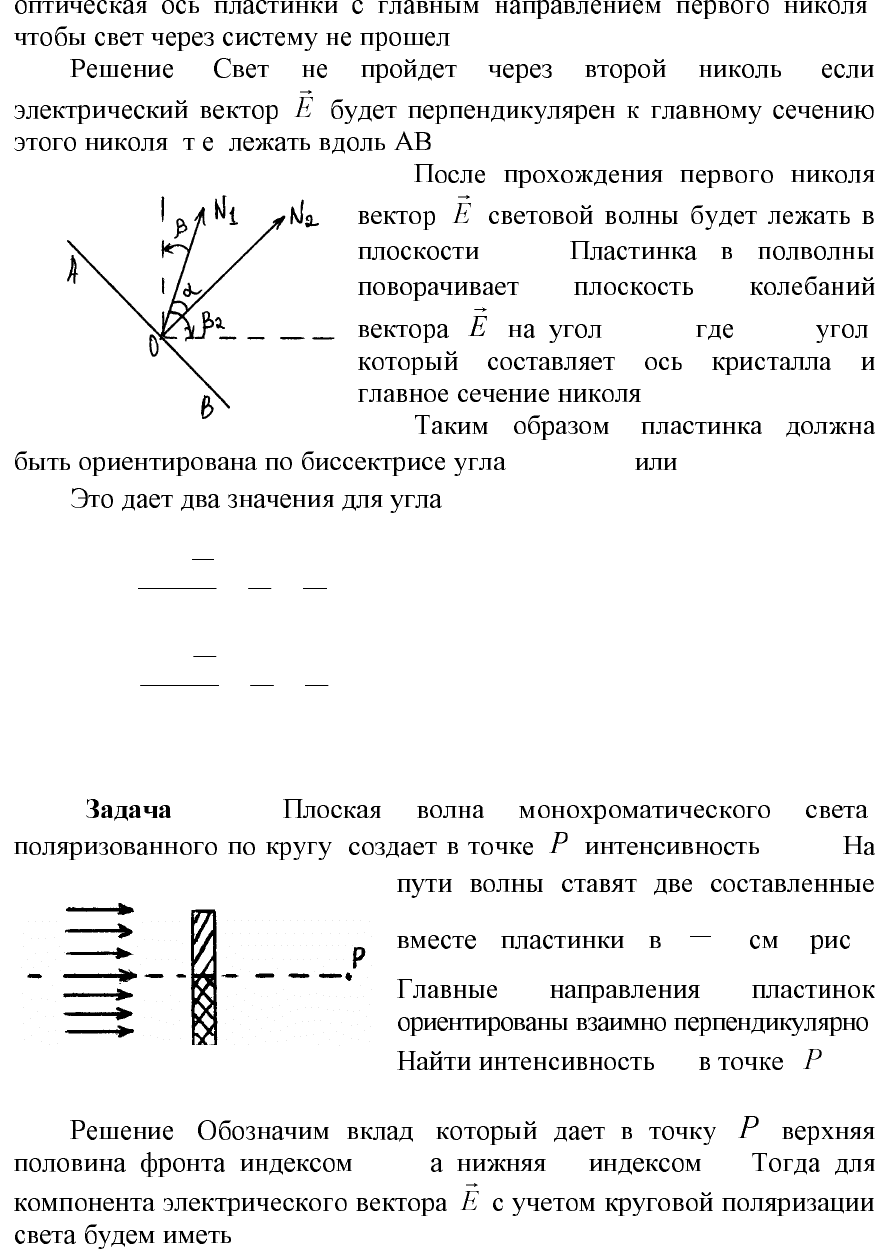
66
,
?
. ,
, . . .
1
N
.
2ϕ
,
ϕ
- ,
.
,
1
AON
OBN
1
.
β:
.304515
4
2
2
2
;601545
242
2
000
2
000
1
=−=−=
−
=
=+=+=
+
=
πα
π
α
β
απ
π
α
β
3.8. ,
,
0
I
.
4
λ
( . .).
.
I
.
. ,
– 1, – 2.

67
.
wtsinEwtcosEE
;wtsinEwtcos
y2x22
y111
⋅+⋅=
⋅+⋅=
2
π
.
. . ,
,
1
1
,
2
-
y2
, . .
+⋅+⋅=
′
⋅++⋅=
′
2
wtsinEwtcosEE
;wtsinE
2
wtcosEE
y2x22
y1x11
π
π
(
)
( )
.wtcosEEE
;wtcosEEE
y2x22
y1x11
⋅+=
′
⋅+−=
′
P
1
E
′
2
E
′
:
(
)
(
)
wtcosEEwtsinEEEEE
y2x2y2x121
⋅+++−=
′
+
′
=
′
. . :
02121
2
1
EE
yy
====
,
( ) ( )
.jwtsinwtcosE
2
1
iwtsinwtcosE
2
1
E
00
++−=
′

68
),
4
wtcos(2wtsinwtcos
)
4
wtcos(2wtsinwtcos
π
π
+=−
−=+
,
.j
4
wtcosi
4
wtcos2E
2
1
E
0
−++=
′
ππ
ω
π
4
+=
′
tt
,
)jtwsinitw(cos
2
E
E
0
⋅
′
+⋅
′
=
′
, ,
2
2
0
2
0
IE
I =≈
,
2
0
I
I =
3.9. ,
,
.
0
45
.
d 50,0
=
.
60,050,0
−
, ,
?
.0090,0
=
∆
.
–
1
Π
(
1
).
:
0

69
.
0
45=
α
.
,
nd∆=∆
λ
π
ϕ
2
.
2
)12(
π
ϕ
+=∆ m
.
,
( )
.
2
12
π
ϕ
+=∆
.
,
:
1
2
4
2
)12(
2
+
∆
=+=∆
m
nd
mnd
λ
π
λ
π
.
,
)12(
10180
7
+
⋅
=
−
m
λ
( ).
(2m+1) = 31
7
1
1081,5
−
⋅=
λ
33 ……
7
2
1045,5
−
⋅=
λ
35 …….
7
3
1014,5
−
⋅=
λ
3.10.
.5.3
0
=
θ
0
45
.
550
=
λ
.

70
0,1
=
∆
.
.
.
1
Π
1
Π
.
. 2
1
.
:
– .
(
0
E
) ,
′
.
′
( ).
,
nd∆=
λ
π
δ
2
,
d
- .
2
Π
0
E
2
Π
(
2
3
).
2
3
, δ
, π .
2
Π
π
λ
π
ϕ
+∆=∆ nd
2
.
, ,
.
4
π
1
Π
2
Π
,
.
I
ϕ
∆+= cos22
11
III
,
1
I
- .
