Рудакова Л.И., Соколова Е.Ю. Практический курс физики. Волновая оптика
Подождите немного. Документ загружается.

11
. ,
.
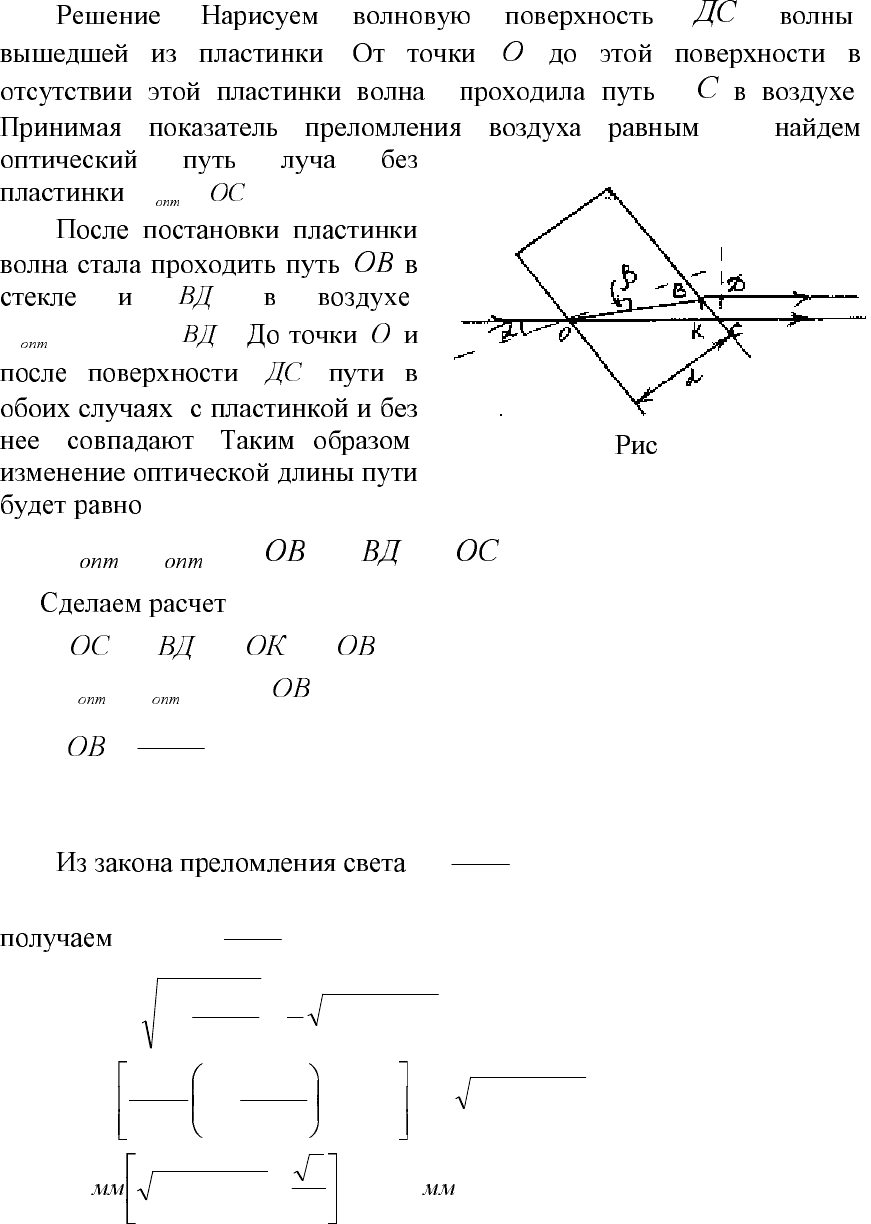
Ο .
1,
:
l =
1
.
;
).()(
2
OBnl +=
(
) . ,
).()()(nll
12
−
+
=
−
:
[ ]
;)cos()(
);
cos(
)
(
)
(
)
(
)
(
12
βα
β
α
−−=∆=−
−
=
=
−
nll
;
cos
β
d
=
.sinsincoscos)cos(
β
α
β
α
β
α
+
=
−
n
sin
sin
=
β
α
:
n
sin
sin
α
β
=
,
[ ]
.548,0
2
3
25,025,21
cossinndcos
n
sin
n
cos
1
d
;sinn
n
1
n
sin
1cos
22
2
22
2
2
=−−=
=−−=−−=
−=−=
ααα
α
β
∆
α
α
β
. 1.6
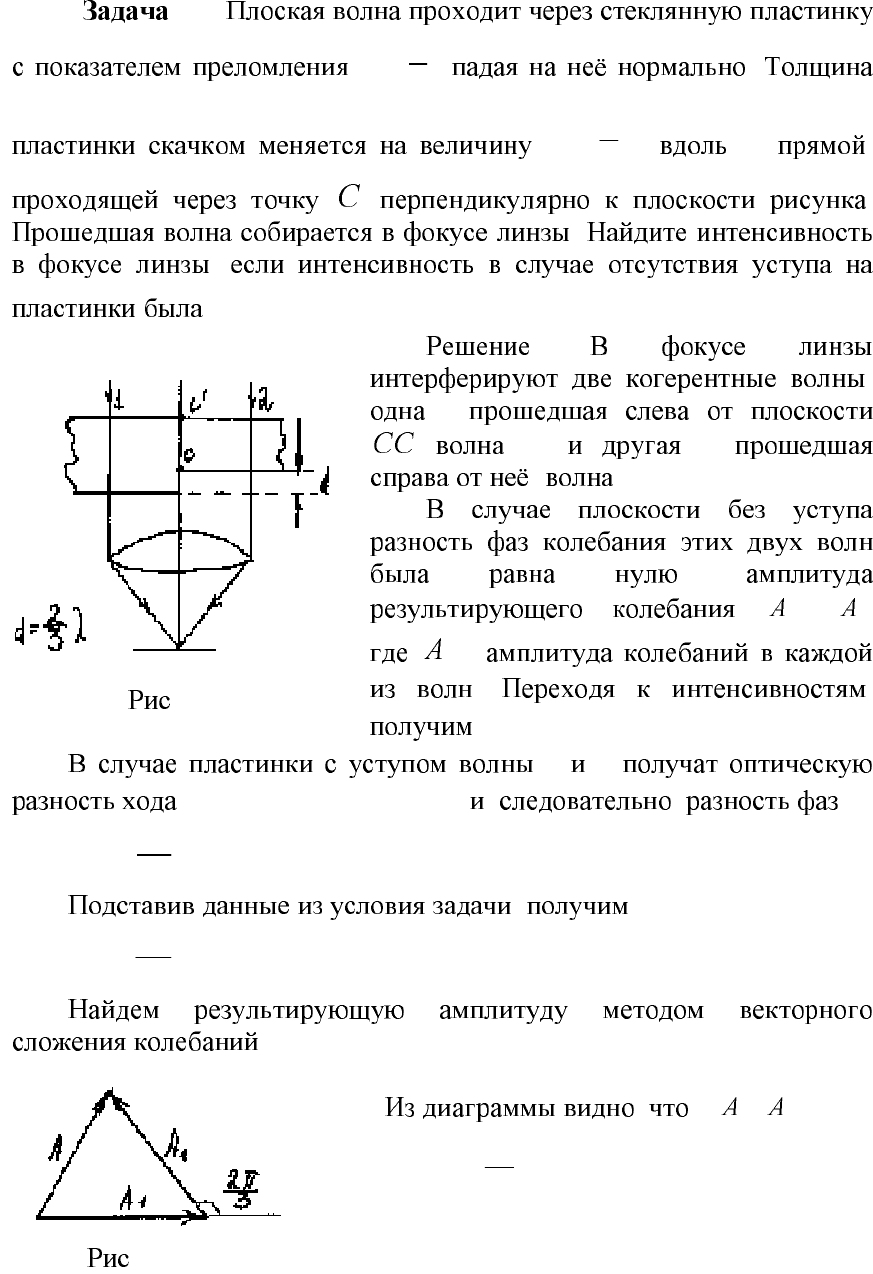
12
1.2.
2
3
=n
, .
λ
3
2
=d
,
.
.
,
0
I
.
.
:
-
′
( 1) –
( 2).
;
10
2=
,
1
-
. ,
10
4II =
.
1 2
),1(
−
=
−
=
∆
ndddn
, ,
).1(
2
−=∆ nd
λ
π
ϕ
,
.
3
2
π
ϕ∆
=
.
,
1
=
4
0
1
I
II ==
. 1.7
. 1.8

13
1.3.
N
:
),)1(cos(
αξ
−+= kwta
k
k
-
(
)
,N,...,2,1k
=
α
- k -
(
)
k −−1
.
.
. ,
.
. ,
ek
−
ek
−
+
)1(
,
α
. ,
,
N
.
. 4.15.
.
,
.
,
.
R
. :
;
2
sin
2
α
R
a
=
2sin2
α
a
R =
.
).
2
sin(
2
α
N
R=
R
,
2
sin
2
sin
α
α
=
N
a
A
.
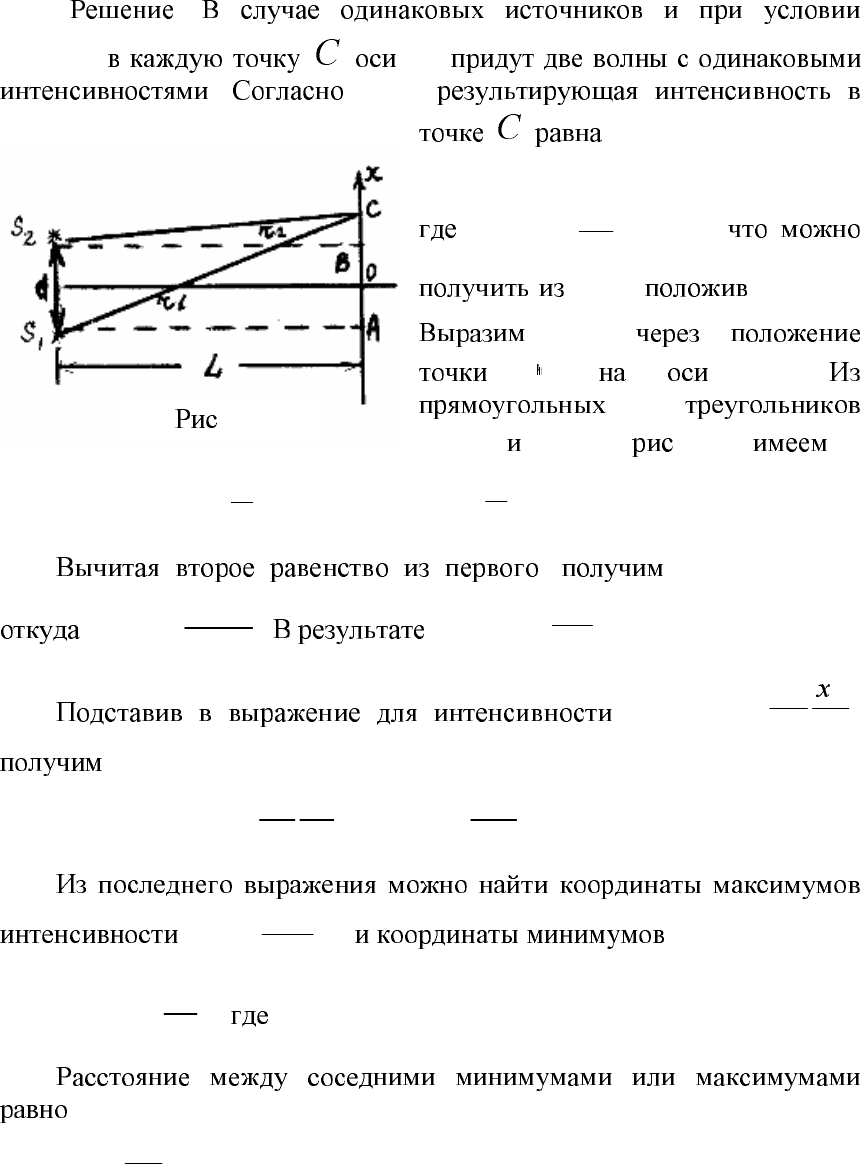
1.4.
λ
d
.
.
)(xI
x
, , ,
L
.
x
O
x
, .
xd,
<<
L
.
. 1.9
14
.
d
<<
L
x
. (1.3),
:
[
]
)cos(12
121
ϕ
ϕ
−
+
=
II
,
),rr(
2
2112
−=−
λ
π
ϕϕ
(1.6),
21
α
α
=
.
21
rr −
. 4.16.
x
.
ACS
1
BCS
2
( . 1.10)
222
1
)
2
(
d
xLr ++=
;
222
2
)
2
(
d
xLr −+=
.
,
xdrr 2
2
2
2
1
=−
,
.
2
21
21
rr
xd
rr
+
=−
.
21
L
xd
rr =−
L
d
λ
π
ϕϕ
2
12
=−
,
( )
L
xd
I
L
xd
IxI
λ
π
λ
π
2
11
cos4)
2
cos1(2 =+=
.
d
Lm
x
λ
=
max
d
L
mx
2
)12(
min
λ
+=
,
...
,
,
,
m
2
1
0
±
±
=
d
L
x
λ
=∆
.
. 4.10.
. 1.10

15
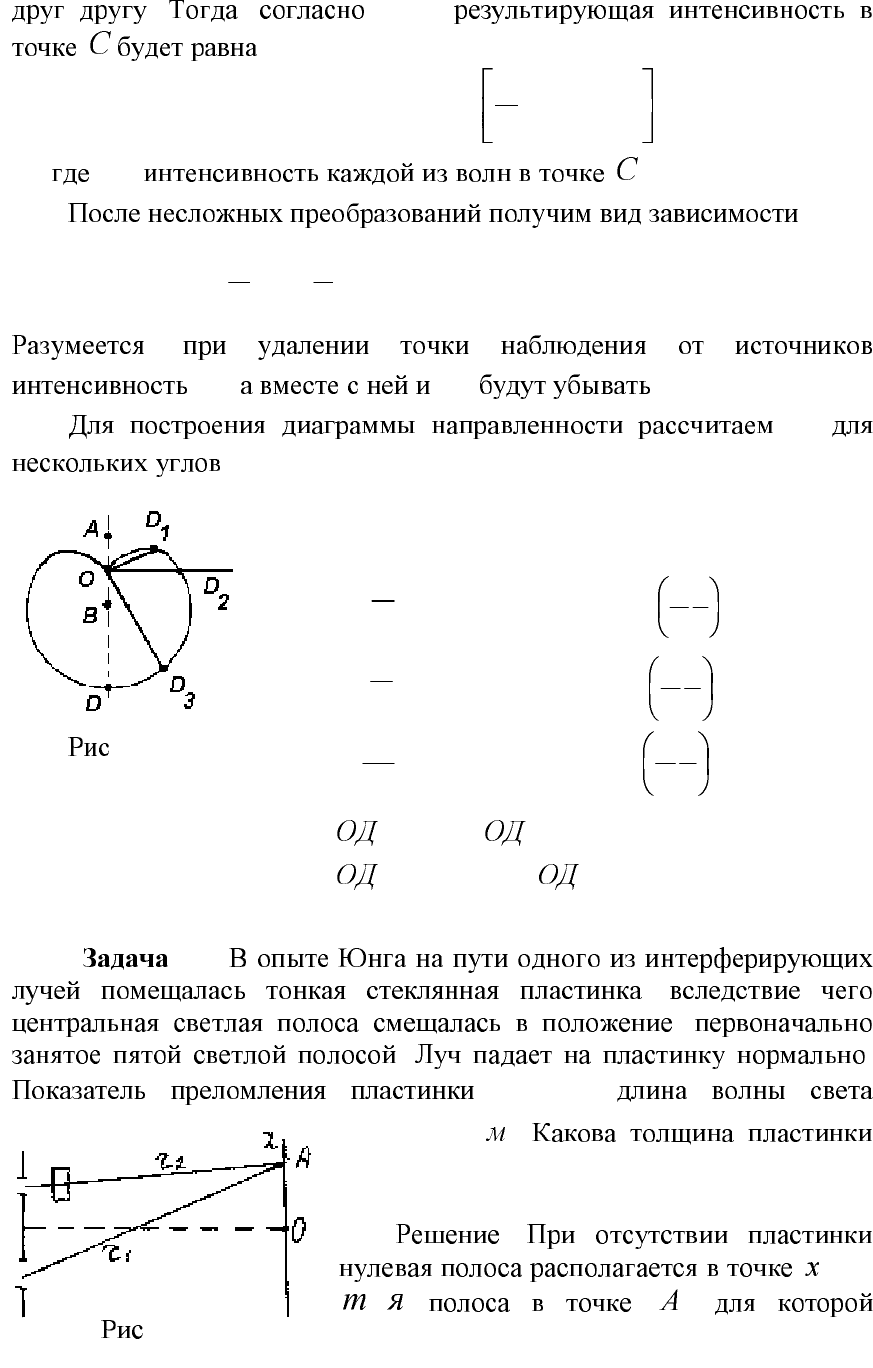
1.5.
4
λ
=d
.
B
2
π
A
:
)
θ
,
( . . 1.11);
)
θ
.
.
.
(
,
>>
d
),
AC
.
θ
cosdB
=
=
−
.
(1.6)
B
.cos
2
2
θ
λ
π
π
ϕϕϕ
d
BA
+=−=∆
) (1.4)
m
πθ
λ
λ
π
π
2cos
4
2
2
=+
,
14cos
−
=
m
θ
.
0
=
m
1cos
−
=
θ
.
π
θ
=
.
(1.5)
πθ
λ
λ
π
π
)12(cos
4
2
2
+=+ m
.
1cos,0,14cos
=
=
+
=
θ
θ
mm
.
, 0
=
θ
.
)
BCAC
≈
,
. 1.11 . 1.12
16
. , (1.3),
( )
),1cos
2
cos1(2cos22
111
++=∆+=
θ
π
ϕ
IIII
1
I
- .
)(
θ
I
).
2
cos
2
(cosI4I
22
1
θ
π
=
,
1
I
,
I
, .
I
θ
:
π
θ
=
,I4II
1max
=
=
0
=
θ
,
0
I
=
3
π
θ
=
,I38,0
4
3
2
cosII
max
2
max
==
π
2
π
θ
=
,I5,0
2
1
2
cosII
max
2
max
==
π
3
2
π
θ
=
,I92,0
4
1
2
cosII
max
2
max
==
π
max3max2
max1max
I92,0,I5,0
,I38,0,I
==
=
=
1.6.
,
,
. .
5,1
=
n
;
7
106
−
×=
λ
.
d
?
.
0
=
,
−
,
. 1.13
. 4.14.
. 1.14

17
.
21
λ
mrr =−
λ
5
21
=−rr
.
A
; ,
ll
21
=
.
11
rl =
.
d
)(
2
dr −
.
,
)1(
222
−
+
=
−
+
=
ndrdrndl
.
:
);1(
21
−
+
=
ndrr
λ
5)1(
21
=−=− ndrr
.
1
5
−
=
n
d
λ
.
d
6
106
−
⋅=
.
1.7.
λ
λ
∆
.
d
,
L
.
? ?
. ,
. 4.9.
.
τ
- .
l
τ
=
- .
, ,
, ,
. ,
.
, ,
, .
, ,
c
rr
t
21
−
=∆
.
. 1.15

18
t
∆
>
τ
(
21
rr −
>
l
),
, .
, 0<
t
∆
<
τ
( ).
,
.
,
.
-
c
rr
τ
=
−
21
. (1.4)
(
)
d
Lrr
21
−
=
,
.
=
d
L
τ
. ν=
λ
c
λ∆
λ
∆
2
c
v =
.
( .(1.13))
v
∆
≈
1
τ
, :
.
d
L
λ
λ
∆
≈
2
, ,
x
N
∆
=
.
1
,
d
L
λ
=∆
- .
λ
λ
∆
≈= 22
1
NN
, .
λ
∆
1
λ
λλλ
∆+=
12
.
. λ
:
d
L
λ
=∆
. .
( . . 1.16).
1
λ
2
λ
. (
1
λ
2
λ
).
,
. ,

19
(
)
um
−
+
1
1
λ
m
−
:
12
λ
λ
λ
∆
+
=
(
)
(
)
11
1
λ
λ
λ
+
=
∆
+
mm
,
λ
λ
∆
=m
.
,
λ
λ
∆
== mN
1
. (
,
, , ,
).
1.8. ,
R 1
=
.
7
105
−
×=
λ
.
d 1,0
=
.
,
.
. ,
.
;
,
.
.
. . 1.17 ,
( ) (
. 4.16.
. 1.16
. 1.17

20
). ( ).
,
, . . ,
.
,
.
. , 1.4
2
1
2
2
2
llR
d
=+− ;
2
2
2
2
2
llR
d
=++
.
1- 2- ;
(
)
(
)
dRllll 2
1212
=+−
.
lll 2
12
≈
+
,
l
dR
ll =−
12
.
,
:
,
2211
rlrl +=+
1221
llrr −=−
.
L
dx
rr =−
21
,
l
dR
L
dx
=
,
l
RL
x =
.
l
RL2
2 =
. ,
xx
∆
≈
2
,
x
∆
-
,
d
L
λ
=∆
.
,
,
:
2
≤
2
∆
;
d
L
l
RL
2
2
λ
≤
.
λ
Rd
l
4
≥
.
l 80
min
≈
