Roy K.K. Potential theory in applied geophysics
Подождите немного. Документ загружается.


16.3 Ta ylor’s Series Expansion and Finite Difference Approach 539
¯g(r)=
k
k=1
A
k
e
µ
k
z
J
0
(µ
k
r) (16.14)
and
g(0)=
k
k=1
A
k
e
µ
k
z
(16.15)
since
J
0
(μ
k
r)=1for r =0
∂g
∂z
z=0
=
k
k=1
µ
k
A
k
(16.16)
∂
n
g
∂z
n
z=0
=
µ
k
n
A
k
(16.17)
Hence
g(+h)=
∞
n=1
h
n
n!
n
k=1
µ
n
k
A
k
. (16.18)
Choosing maximum number of k = 3 and minimum number of n = 11, we get
¯g(1)=A
1
J
0
(µ
1
)+A
2
J
0
(µ
2
)+A
3
J
0
(µ
3
) (16.19)
¯g(2)=A
1
J
0
√
2µ
1
+A
2
J
0
√
2µ
2
+A
3
J
0
√
2µ
3
. (16.20)
For r = 0, S, S
√
2,
g(+h)=
11
n=0
n
n!
3
k=1
µ
n
k
A
k
. (16.21)
16.3.3 An Example of Analytical Continuation Based
on Synthetic Data
Roy (1966) computed downward continued gravity data based o n computed
gravity values due to an infinitely long buried cylinder buried at a depth
H = h.The analytical continuation depths are h-2∆h, h-∆h, h, h + ∆h, h +
2∆h. The depths chosen were 0.50, 0.75, 1.00, 1.25, 1.50, 1.75 and 2.00. The
depth interval is 0.25 unit.The grid interval was also 0.25 unitsThe working
formula for computation of the gravity field is given in Chap. 3 (Sect. 3.7),
(3.33). Figures 16.2 and (16.11) are the guidelines for downward continuation
of gravity field.
Figure 16.3 shows that the central peak of the gravitational anomaly
increases at a very faster pace with gradual increase in depth of continua-
tion. Figure 16.4 show that beyond a certain depth, the gravitational anomaly
explodes i.e., heading towards an infinitely high value. The point of maximum
gradient or inflection gives estimated depth of the body.
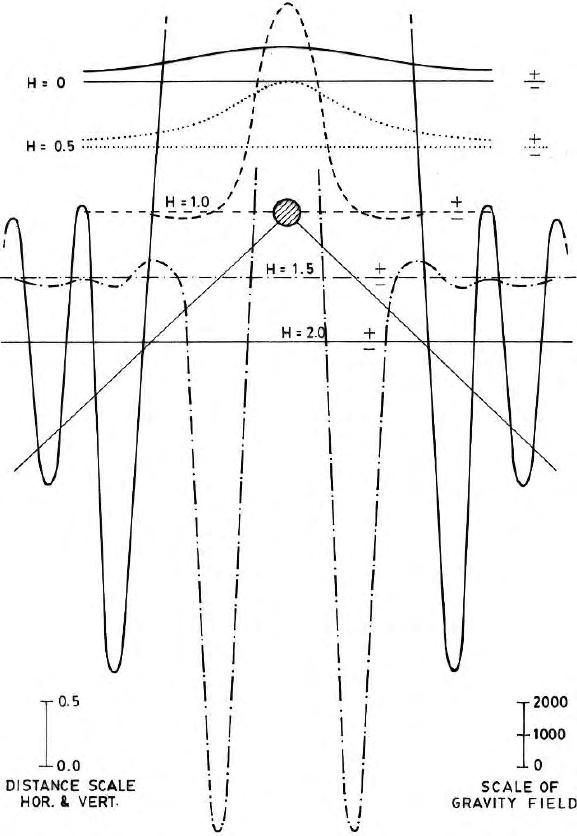
540 16 Analytical Continuation of Potential Field
Fig. 16.3. Analytical continuation of synthetic gravity data generated due to an
infinitely long buried cylinder (Roy 1966)
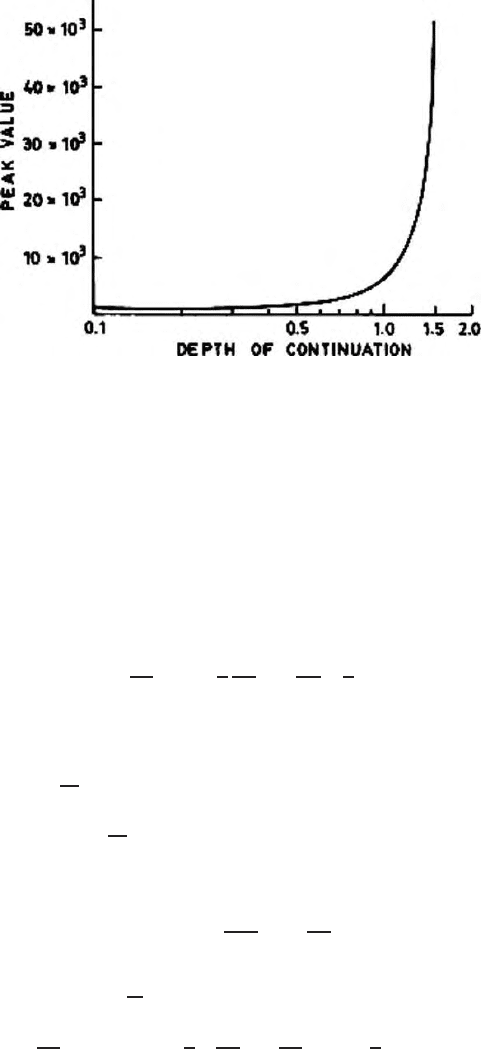
16.4 Green’s Theorem and Integral Equations for Analytical Contin uation 541
Fig. 16.4. Gradual increase in amplitude of the peak value of the gravitational
anomaly in different stages of dow nward continuation; point of inflection of the
curve gives the depth estimation of the causative body (Roy 1966)
16.4 Green’s Theorem and Integral Equations
for Analytical Continuation
Upward continuation integral based on the Green’s Theorem is presented in
this section Roy (1962), Blakely (1996). From Green’s third formula (Chap. 10,
(10.29)), the p otential φ
p
inside a source fre e region R bounded by a surface
S (Fig. 16.5) is given by
φ
ρ
=
1
4π
S
1
r
∂φ
∂n
− φ
∂
∂n
1
r
ds (16.22)
where n is the direction outward normal to S and r is the distance between the
point and the surface element ds. It is known from the uniqueness theorem
that either φ or
∂φ
∂n
alone specified on S, should completely determine the
potential distribution inside S (Chap. 7.14). It should, therefore, be possible
to eliminate either φ or
∂φ
∂n
from (16.22). Assuming both φ and G
′
as harmonic,
where G
′
is another scalar function, we can write from Green’s Second identity
in symmetric form as
0=
S
φ
∂G
′
∂n
− G
′
∂φ
∂n
ds (16.23)
Multiplying (16.23) by −
1
4π
and adding it to (16.22) we get
φ
ρ
=
1
4π
S
G
′
+
1
r
∂φ
∂n
− φ
∂
∂n
G
′
+
1
r
ds (16.24)
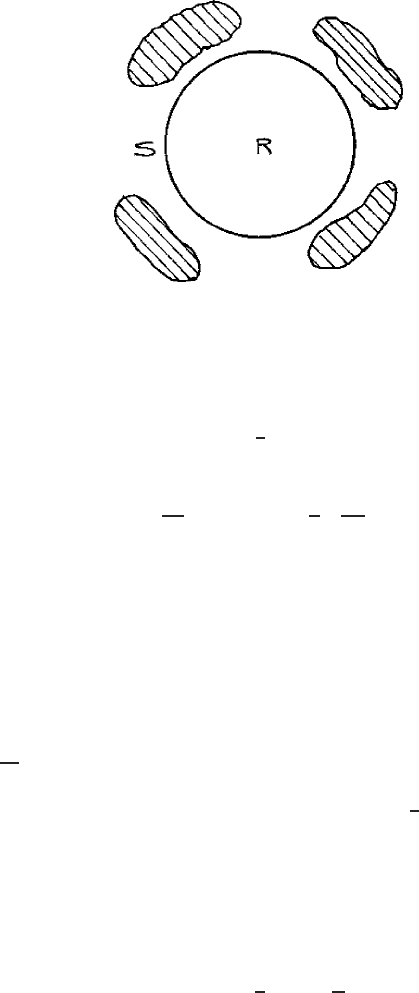
542 16 Analytical Continuation of Potential Field
Fig. 16.5. Source free region R bounded by the surface S; all the source (masses)
are outside S
If G
′
is so chosen that in addition to its being a solution of Laplace equation
in R, it also has a normal derivative at any point on S and is equal to the
negative of the normal derivative or
1
r
at the same point, then the (16.24)
simply reduces to
φ
ρ
=
1
4π
S
G
′
+
1
r
∂φ
∂n
ds. (16.25)
In (16.25) φ is eliminated at the cost of G
′
.ItisaGreen’sfunction.G
′
will
depe n d upon the nature of the surface S. Usefulness of (16.25) is depended
upon getting a suitable value of G
′
for specific cases. The surface S of Fig. 16.6
consists of two portions, i.e., a flat ground surface at z = 0 and an hemispher-
ical surface of infinite radius. All the sources are below the ground surface
and are, therefore, outside R as required. The surface integration in (16.25)
now reduces simply to an integration over the plane z = 0 (ground surface)
because
∂φ
∂n
= 0 at all points on the infinite hemisphere. The outward drawn
normal becomes identical with the conventional positive direction of z. With
the surface S defined like this, G
′
is obviously given by
1
r
,where
r=
x
2
+y
2
+(z+h)
2
1/2
and
r
′
=
x
2
+y
2
+(z− h)
2
1/2
(16.26)
as may be verified by differentiating
1
r
and
1
r
′
with respect to z and then
putting z = 0. Thus (16.24) becomes
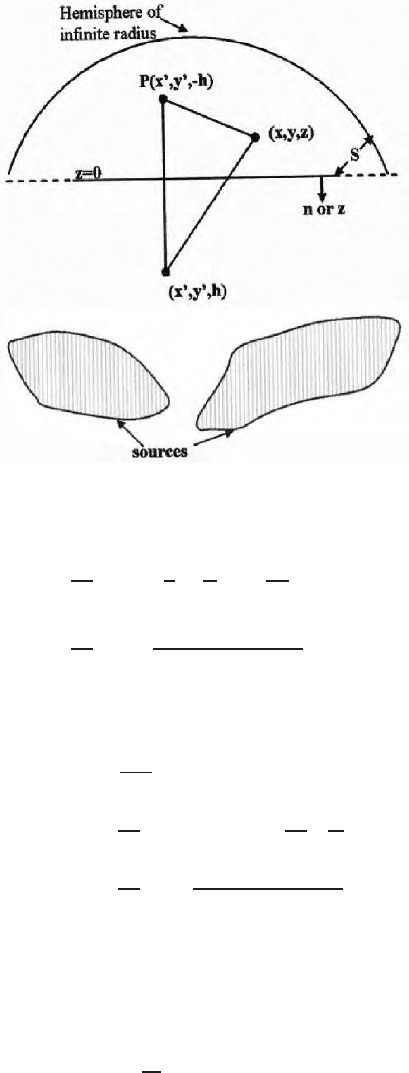
16.4 Green’s Theorem and Integral Equations for Analytical Contin uation 543
Fig. 16.6. Shows source free region R bounded by a horizontal surface S and hemi-
sphere of infinite radius
φ
ρ
=
1
4π
z=0
1
r
+
1
r
′
z=0
∂φ
∂z
z=0
dx dy (16.27)
=
1
2π
z=0
g(x, y, 0) dx dy
(x
2
+y
2
+h
2
)
3/2
. (16.28)
Gravity field at the point P (Fig. 16.6) is given by
g(0, 0, −h) =
∂φ
ρ
∂z
z=−h
=
1
2π
g(x, y, 0)
∂
∂z
1
R
z=−h
=
h
2π
g(x, y, 0) dx dy
(x
2
+y
2
+h
2
)
3/2
(16.29)
where R
2
=x
2
+y
2
+z
2
.
So far as gravity is concerned, elimination of φ
p
from (16.22) is suitable
because
∂φ
p
/∂n
ultimately turns out to be g, the vertical component of
gravitational attraction due to anomalous masses. In many geophysical mea-
surements other components may also be measured. For such cases, it may
become necessary to eliminate
∂φ
∂n
from (16.22) and one finally gets

544 16 Analytical Continuation of Potential Field
φ (0, 0, −h) =
h
2π
z=0
φ (x, y, 0) dx dy
(x
2
+y
2
+z
2
)
3/2
. (16.30)
Equation (16.30) is valid for any measurable solution of Laplace’s equation.
Equation (16.28) is same as (16.30) written for ‘g’.
For potential or field at any point on an upper plane, one may thus replace
the real sources by an imaginary laminar distribution on a lower parallel plane
with a surface density of g (x, y, 0)/2πG Here G is the gravitational constant.
It can be proved that the areal density g (x, y, 0)/2πG, when integrated over
the entire plane, yields the anomalous mass causing the gravity anomaly.
16.5 Analytical Continuation using Integral Equation
and Taking Areal Averages
Peter’s (1949) proposed the following techniques for upward and downwa rd
continuation of potential field. Peter presented his theory using magnetic field,
here his formulation is shown in terms of the gravity field.
16.5.1 Upward Continuation of Potential Field
We have seen from (16.30) that gravitational field at any height h can b e
written in terms of the surface values of the gravity field as
g(α, β, −h) =
1
2π
∞
−∞
∞
−∞
g(x, y, 0) h dx dy
(x −α)
2
+(y− β)
2
+h
2
3/2
. (16.31)
Negative sign is for upward continued values.
Let
x −α =r cosθ
and
y − β =r sinθ (16.32)
then
g(α, β, −h) =
∞−
0
g(r)h r dr
(r
2
+h
2
)
3/2
(16.33)
where ¯g (r) is the average value of gravity at a point within the radial distance
‘r’. Equation 16.33 can now be written as

16.5 Analytical Continuation using Integral Equation 545
g(α, β, −h) ≈
g(0)+¯g(r
1
)
2
r
1
0
hrdr
(r
2
+h
2
)
3/2
+
¯g(r
1
)+¯g(r
2
)
2
r
2
r
1
hrdr
(r
2
+h
2
)
3/2
+
¯g(r
2
)+¯g(r
3
)
2
r
3
r
2
hrdr
(r
2
+h
2
)
3/2
+ ............................................. . (16.34)
Since
hrdr
(r
2
+h
2
)
3/2
≈−
h
(r
2
+h
2
)
1/2
(16.35)
we can write
g(α, β, −h) =
g(0)
2
)
1 −
h
(h
2
+r
2
1
)
1/2
*
+
¯g(r
1
)
2
)
1 −
h
(h
2
+r
2
2
)
1/2
*
+
¯g(r
2
)h
2
)
1
(h
2
+r
2
1
)
1/2
−
1
(h
2
+r
2
3
)
1/2
*
+
¯g(r
3
)h
2
)
1
(h
2
+r
2
2
)
1/2
−
1
(h
2
+r
2
4
)
1/2
*
......................................................................
......................................................................
+
¯g(r
n
) .h
2
)
1
h
2
+r
2
n−1
1/2
−
1
h
2
+r
2
n+1
1/2
*
.
+ ............................................. (16.36)
The (16.36) is used to determine the upward continued potentials. The values
of r
1
, r
2
, r
3
.............r
n
and the coefficients of ¯g(r)forh=1andh=2aregiven
in Table 16.1. Depending upon the need, coefficients for any value of the h
n
can b e determined.
Radii of the Peter’s circles for upward continuation can approximately be
written as
(i)
√
2=
√
1
2
+1
2
(ii)
√
5=
√
2
2
+1
2
(iii)
√
8.5 ≈
√
2
2
+2
2
≈
√
3
2
(iv)
√
17 =
√
4
2
+1
2
(v)
√
34 ≈
√
6
2
≈
√
4
2
+4
2
(vi)
√
58 ≈
√
6
2
+5
2
546 16 Analytical Continuation of Potential Field
Table 16.1. Coefficients of ¯g (r) for Different Level of Continuation
Radius Coefficient of
g(r)forh=1
Coefficient of
g(r)forh=2
0 0 0.1464 0.0528
1 1 0.2113 0.0918
2
√
2 0.1494 0.1139
3
√
5 0.1265 0.1254
4
√
8.5 0.0863 0.1151
5
√
17 0.0777 0.1206
6
√
34 0.0528 0.0912
7
√
58 0.0345 0.0637
8
√
99 0.0206 0.0320
9
√
125 0.0945 0.1866
(vii)
√
99 ≈
√
10
2
≈
√
7
2
+7
2
(viii)
√
125 ≈
√
10
2
+5
2
Gravity data used for interpretation are available in the form of contour maps
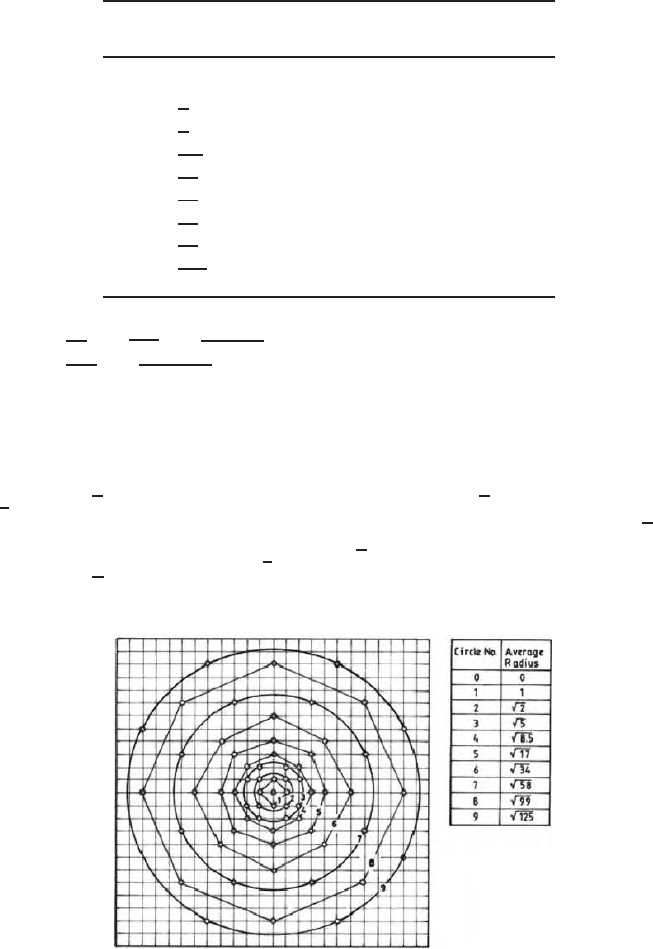
where the gravity values are taken at the grid points. Figure 16.7 shows the
grid point and Peter’s circles. If the intensity is to be calculated one unit
above the plane z = 0, for h = 1 and r = 1, then the term multiplying g (r
1
)is
1
2
'
1 −1/
√
2
(
=0.1464. Similarly a circle with radius
√
2 about 0, four values
lie on this circle and ¯g(r
2
) is one fourth the sum of the four values
r
2
=
√
2
.
The term multiplying ¯g(r
1
)is
1
2
'
1 − 1/
√
3
(
=0.2113. The values of r
3
can be
taken as
√
5.
Fig. 16.7. Peter’s circle for areal averaging
16.5 Analytical Continuation using Integral Equation 547
Thecircleofradiusr
3
passes through eight points on the corner of an
o ctagon. The values at these eight point a re used to compute averages.
16.5.2 Downward Continuation of Potential Field (Peters
Approach)
Using Taylors series expansion, one can write
g(+h)=g(0)+ h
∂g
∂z
z=0
+
h
2
2!
∂
2
g
∂z
2
z=0
+ .............. (16.37)
and
g(−h) = g (0) − h
∂g
∂z
z=0
+
h
2
4!
∂
4
g
∂z
4
z=0
+ .............. . (16.38)
Adding (16.37) and (16.38) we get
g(0, 0, h) =2
g(0, 0, 0) +
h
2
2!
∂
2
g
∂z
2
z=0
+
h
4
4!
∂
2
g
∂z
4
z=0
+---------------------------]− g(0, 0, −h) .
(16.39)
Since in a source free region the potential satisfies Laplace equation, we can
write
∂
2
g
∂z
2
= −
∂
2
g
∂x
2
+
∂
2
g
∂y
2
. (16.40)
In a cylindrical polar coordinate we can write
g(0, 0, h) =g (0, 0, 0) −
h
2
2
∂
2
∂r
2
+
1
r
∂
∂r
¯g(r)
+
h
4
4!
∂
2
∂r
2
+
1
r
∂
∂r
2
¯g(r)−
h
6
6!
∂
2
∂r
2
+
1
r
∂
∂r
3
¯g(r)
+ ............................................. . (16.41)
It can be shown from Green’s Theorem that ¯g (r) is an even function and it
may be written in the form
¯g(r)=b
0
+b
2
r
2
+b
4
r
4
+b
6
r
6
+ ............ . (16.42)
If we carry out the operation as indicated in (16.41), we can find
∂
2
∂r
2
+
1
r
∂
∂r
¯g(r)=4b
2
(16.43)
∂
2
∂r
2
+
1
r
∂
∂r
2
¯g(r)=6.4b
4
(16.44)
∂
2
∂r
2
+
1
r
∂
∂r
3
¯g (r) = 2304b
6
. (16.45)
548 16 Analytical Continuation of Potential Field
The (16.39) for the continuation down ward becomes
g(0, 0, h)
∼
=
2
b
0
− 2b
2
h
2
+
8
3
b
4
h
4
−
16
5
b
6
h
6
+ .......
−g(0, 0, h) . (16.46)
The values of b
0
, b
2
and b
4
are obtained by least squares solution of the
abridged form of (16.42)
g(0, 0, h)
∼
=
b
0
+b
2
r
2
+b
4
r
4
. (16.47)
Using the average values of ¯g (r) around the circles of radius 0, 1,
√
2,
√
5,
√
8.5,
√
17,
√
34,
√
58,
√
99, the values of b
0
, b
2
, b
4
, obtained by the least
squares method as (Peters 1949).
b
0
=0.2471¯g(0)+0.2351¯g(1)+0.2234¯g
√
2
+0.1874¯g
√
5
+0.1521¯g
√
8.5
+0.0717¯g
√
17
− 0.0449¯g
√
34
− 0.1095¯g
√
58
+0.0500¯g
√
99
(16.48)
b
2
= −0.0119 ¯g(0)− 0.0105¯g(1)− 0.0091¯g
√
2
− 0.0053¯g
√
5
− 0.0011¯g
√
8.5
+0.0077¯g
√
17
+0.0192¯g
√
34
+0.0218¯g
√
58
− 0.0108¯g
√
99
(16.49)
b
4
= −0.00010 ¯g(0)+0.00009¯g(1)+0.0007¯g
√
2
+0.00004¯g
√
5
− 0.¯g
√
8.5
− 0.00009¯g
√
17
− 0.00020¯g
√
34
− 0.00020¯g
√
58
+0.00020¯g
√
99
(16.50)
These values are substituted in (16.47) to get the coefficients for the circles.
By combining the coefficients for continuation upward g (0, 0, −h), given in
Table 16.2. Values of the coefficients for down ward continuation
a
0
a
2
a
4
g (0) 0.2473 −0.0122 0.0001
¯g (S) 0.2353 −0.0107 0.00009
g
S
√
2
0.2236 −0.0093 0.00007
¯g
S
√
5
0.1895 −0.0055 0.00004
¯g
S
√
8.5
0.1521 −0.0013 −0.000007
¯g
S
√
17
0.0714 0.0075 −0.0009
¯g
S
√
34
0.460 0.0190 −0.00020
¯g
S
√
58
0.1124 0.0215 −0.0021
¯g
S
√
99
−0.0432 −0.0116 +0.00020
