Roy K.K. Potential theory in applied geophysics

Подождите немного. Документ загружается.

7.4 Laplace Equation in Cartesian Coordinates 159

φ =



′

−α

cos α

y. (7.39)

Applying the third boundary condition, we get:



′

−α

cos

. (7.40)

Therefore

cos

⇒ α

nπ

where n = 1, 3, 5, 7,..............

The expression for the potential changes to the form

φ =



′

−

nπ

cos

nπ

. (7.41)

Applying the second boun d ary condition, (7.41) becomes:

Pcos

πy

′

cos

nπy



′

cos

πy

′

cos

3πy

′

cos

5πy

+ ......



. (7.42)

Equating the coeﬃcients of cos

πy

on both the sides, one gets:

P=c

′

for n = 1, therefore c

′

9··········

=0.

Therefore the ﬁnal solution of the problem is:

φ =Pe

−

πx

cos

πy

. (7.43)

Problem 2

A ﬁnite rectangular conductor of length ‘a’ and width ‘b’ is placed in the

xy plane placing the corner A of the rectangle at the origin. The prescribed

potentials at the boundaries are as follows (Fig. 7.6)

Φ=0atx=0

φ =0atx=a

φ =0aty=0

φ =f(x), at y = b

Find the p otential at any p oint on the plate. The solution of the Laplace

equation :

∂

= 0 (7.44)

160 7 Solution of Laplace Equation

Fig. 7.6. A two dimensional potential problem with potentials prescribed in all the

b oundaries

are

(i) e

αx

, e

−αx

, sin αy, cos αy

(ii)

sin αx, cos αx, e

αy

, e

−αy

(7.45)

and the general solution of the problem is written as :

φ =

∞



n=o

cos α

x + B

sin α



+ D

−α



. (7.46)

Va l u es of these arbitrary constants are determined using the b oundary con-

ditions.

Applying the ﬁrst boundary condition, we get:

0=ΣA



−α



. (7.47)

The right hand side expression of (7.47) will be zero when A

= 0. Therefore

the general expression for the potential reduces to

φ =

∞



n=0

sin α



−α



. (7.48)

Applying the second boundary condition, we get:

0=Σsinα



′

−α



(7.49)

where C

′

and D

′

Equation (7.49) will be 0 if sin α

a=0

⇒ α

a=nπ

⇒ α

nπ

. (7.50)

φ =



Sin

nπx



′

nπy

′

−

nπy



. (7.51)

7.4 Laplace Equation in Cartesian Coordinates 161

Applying the third boundary condition, we get:



sin

nπx

′

) . (7.52)

Equation (7.52) will b e 0 if,

′

⇒ C

′

= −D

′

. (7.53)

Hence the expression for the potential becomes

φ =



sin

nπx

′



nπy

− e

−nπy





′

sin

nπx

sinh

nπy

(7.54)

where, F

′

is a new constant.

Now applying the fourth boundary condition, we get:

f(x) =



′

sinh

nπb

. sin

nπx

. (7.55)

Multiplying both the sides by sin

mπx

and integrating from a to 0, we get:



f(x)sin

mπx

dx =





′

sin h

nπb

. sin

nπx

sin

mπx

dx. (7.56)

Since



sin nx sin mx dx = 0 for m =n

for m = n,

therefore, from (7.55), one can write

′

sinh

mπb



f(x)sin

mπx

dx. (7.57)

Hence, the general solution of the problem i s

φ =



sin

mπx

sinh

nπy

. (7.58)

162 7 Solution of Laplace Equation

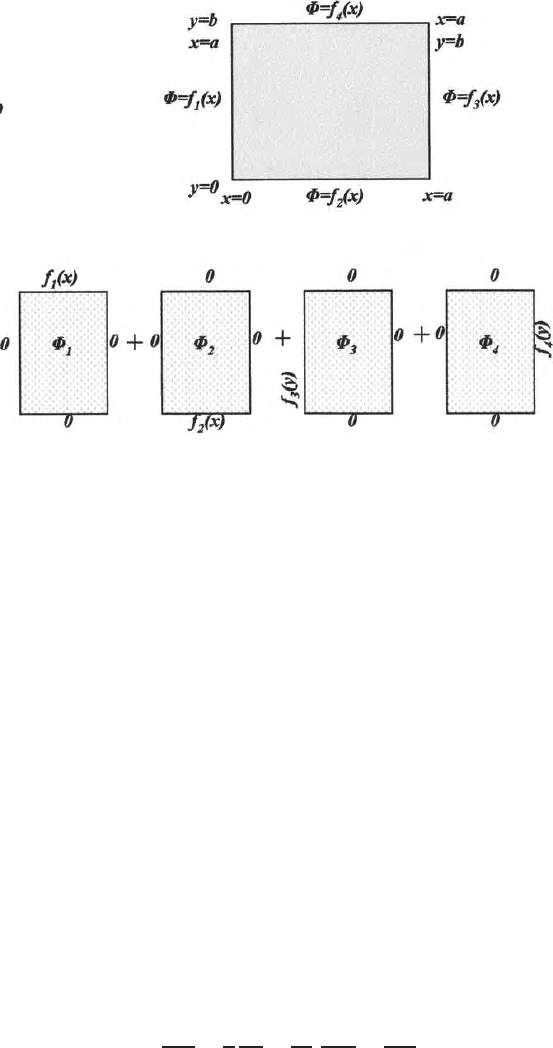
Fig. 7.7. A break up of a two dimensional problem into four parts to make it a

easily solvable problem

Problem 3

Find the potential at any point inside a rectangular conductor of length ‘a’

and width ‘b’ placed in the xy planes when the following boundary conditions

are prescrib ed, i.e., for (Fig. 7.7)

x=0, φ =f

(x)

y=0, φ =f

(x)

x=a, φ =f

(x)

y=b, φ =f

(x)

This problem can be solved by breaking the problem into fou r problems similar

to that discussed in the previous section, get the potential at a point for four

problems and add them up. Since the potentials are scalars and the principle

of superposition is valid, we can get

φ = φ

+ φ

. (7.59)

7.5 Laplace Equation in Cylindrical Polar Coordinates

Laplace equation in cylindrical coordinate is :

∇

φ =

∂

∂ρ

∂φ

∂ρ

∂

∂ψ

∂

∂z

= 0 (7.60)

7.5 Laplace Equation in Cylindrical Polar Coordinates 163

where the coordinates are ρ (along the radial direction), Ψ (along the

azimuthal direction) and z (along the vertical direction). Applying the method

of separation of variables we can write :

φ =R(ρ)Ψ(ψ)Z(z)

where, R, Ψ and Z are respectively the functions of ρ, Ψ and z only. Therefore,

from (7.60) we can write

ΨZ

dρ

ΨZ

dρ

dψ

+ Rψ

=0. (7.61)

Now dividing the equation by RΨZ, we get

dρ

Rρ

dρ

dψ

=0. (7.62)

Let us choose

= α

. (7.63)

Multiplying the (7.62) by ρ

,weget:

dρ

+ α

dψ

=0. (7.64)

We, next put

dψ

= −β

(7.65)

and obtain :

dρ

+ α

− β

= 0 (7.66)

which can be rewritten as

dρ



−



R=0. (7.67)

This equation is known as Bessels equa tion.

Alternately, we can have the second set of equations as follows:

= −α

(7.68)

dψ

= −β

(7.69)

dρ

−





R = 0 (7.70)

Equation (7.70) is a modiﬁed Bessels equation.

Now let us examine the dependence of potential function on ρ, ψ,zand

the corresponding changes in the expressions for potentials.

164 7 Solution of Laplace Equation

7.5.1 When Potential is a Function of z ,i.e., φ =f(z)

The Laplace equation takes the form

=0, or φ = Az + B (7.71)

where A and B are constants. The potential at a point is gradually increasing

with z. This is the potential function due to an inﬁnite plate, discussed in the

previous section.

7.5.2 When Potential is a Function of Azimuthal Angle Only

i.e., φ =f(ψ)

The Laplace equation changes to the form

dψ

=0, or φ =Cψ + D (7.72)

where C and D are constants. A circular resistance carrying current can create

this type of potential functions.

7.5.3 When the Potential is a Function of Radial Distance,

i.e., Φ = f(ρ)

The Laplace equation becomes

∂

dρ

∂φ

∂ρ

= 0 (7.73)

⇒

∂

∂ρ



∂φ

∂ρ



∂φ

∂ρ

=N,∂φ =

∂ρ

Therefore the solution of this equation is :

φ =M1nρ + N (7.74)

where M and N are constants to be determined from the boundary conditions.

Let us take a n example.

Problem

Two inﬁnitely long cylinders of radius ‘a’ and ‘b’ are placed co-axially. The

potentials at the outer boundary at radius ‘b’ and the inner boundary at

radius ‘a’ are respectively 0 and V

. Find the potential at any point in the

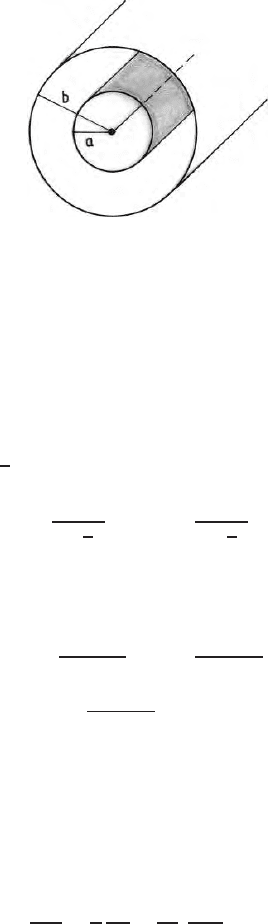
7.5 Laplace Equation in Cylindrical Polar Coordinates 165

Fig. 7.8. Potential inside a cylinderical shell when the potentials are prescribed in

the inner and outer b oundaries

annular space between the two cylinders (Fig. 7.8) Applying the boundar y

conditions, we get:

0=M1nb+N

= M1n a + N (7.75)

Therefore, V

=M1n





and N =





. ln b (7.76)

The potential at any point at a radial distance ρ from the axis of the coaxial

cylindrical bodies is given by

ln (a/b)

ln ρ −

ln b

ln (a/b)

ln (ρ/b)

ln (a/b)

. (7.77)

7.5.4 When Potential is a Function of Both ρ and ψ,

i.e., φ =f(ρ, ψ)

The Laplace equation becomes

∂

dρ

∂φ

∂ρ

∂

∂ψ

=0. (7.78)

Applying the method of separation of variables i.e.,

φ =R(ρ)Ψ(ψ)

we get two equations

166 7 Solution of Laplace Equation

dψ

= −n

(7.79)

and

dρ

−

R=0. (7.80)

The solution of the (7.79) is

φ =(Acosnψ +Bsinnψ). (7.81)

The solution of the (7.80) can be determined as follows:

Multiplying the (7.80) by ρ

,weget

dρ

+ ρ

dρ

− n

R=0. (7.82)

Let

θ =log

, then ρ =e

So,

dρ

dθ

dρ

dθ

−θ

⇒

dρ



dρ



dρ



−θ

dθ



−θ

dθ



−θ

dθ



−θ



−θ

dθ

− e

−θ

dθ



−2θ



dθ

−

dθ



Substituting these values one gets

dθ

−

dθ

− n

R=0

or,

dθ

− n

R=0

or,

R=A

nθ

−nθ

−n

(7.83)

Therefore, the general solution of Laplace equation when Φ = f(ρ, ψ), is

φ =

∞



cos nψ +B

sin nψ)



−n



. (7.84)

7.5 Laplace Equation in Cylindrical Polar Coordinates 167

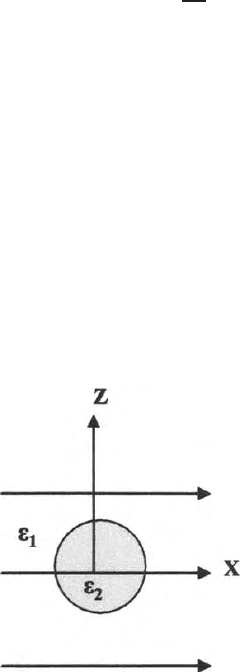
Problem 1

An inﬁnitely long cylinder of dielectric constant ∈

is placed in a medium

of dielectric constant ∈

with the axis of the cylinder oriented along the z-

direction. The cylinder is placed in an uniform ﬁeld, i.e., the source and sink

are assumed to be at inﬁnity (Fig. 7.9).

Find the p otential at any point both inside and outside the cylindrical

body.

In a direct current ﬂow ﬁeld, we assume a cylindrical conductor of electrical

conductivity σ

is placed in an homogeneous medium of conductivity σ

.The

boundary value problem will essentially remain the same. The ﬁeld is assumed

to be perpendicular to the axis of the cylinder and is assumed to be parallel

to the x-axis.

Since

E=−gradφ = −

∂φ

∂x

(7.85)

where φ is the potential function. We get

Ex.x=−φ + Constant. (7.86)

Therefore, the source potential is :

= −Ex.x+A

where A is a constant and x is the of the point assumed origin. A is dropp ed

while computing the perturbation potential. In an uniform ﬁeld E

,ina

medium of dielectric constant, ∈

and in the presence of an anomalous b ody

of contrasting physical property ∈

, an anomalous or perturbation potential

will be generated. It will be added up to the source potential in an uniform

ﬁeld. This perturbation potential will gradually die down with distance of the

point of observation from the centre of the cylinder,the anomalous body.

Fig. 7.9. An inﬁnately long cylinder of dielectric constant ∈

is placed in a medium

of dielectric constant; ∈

in the presence of an uniform ﬁeld

168 7 Solution of Laplace Equation

Potential at a point both outside and inside a cylinder can be written as:

= φ

+ φ

′

(potential outside)

= φ

+ φ

′′

(potential inside) (7.87)

Here φ

′

and φ

′′

are the perturbation potentials outside and inside the body.

The perturbation potential part also must satisfy Laplace equation.

Therefore

∇

′

=0and∇

′′

= 0 (7.88)

assuming the radius vector is at an angle ψ with the x-axis

= −E

x=−E

ρ cos ψ (7.89)

where Ψ is the a ngle between the radius vector ρ and the x-axis. Since the

source po tential has a cos Ψ term, the perturbation potential will also have

cos Ψ terms only. The g eneral expression for the perturbation potential, when

it is a function of ρ and Ψ and independent of z, reduces down to

′

∞



n=o

cos nψ, ρ

−n

(potential outside) (7.90)

Here ρ is the radial distance from the axis of the cylinder. Since the pertur-

bation potential will gradually die down with distance from the centre of the

cylinder D

−n

will b e the appropriate potential function for outside region.

Similarly, the perturbation potential inside the body will be given by C

the appropriate potential function. Hence

′′

∞



n=o

cos nψρ

. (7.91)

Because when ρ tends to zero, D

−n

in (7.84) tends to inﬁnity. Since poten-

tial inside a body, when placed in an uniform ﬁeld, cannot be inﬁnitely high

Therefore, ρ

−n

cannot be a potential function inside the body. Here f

and g

We can now write down the potentials outside and inside the

body respectively as:

= −Eρ cos ψ +

∞



n=0

cos nψρ

−n

and

= −Eρ cos ψ +

∞



n=0

cos nψρ