Roy K.K. Potential theory in applied geophysics
Подождите немного. Документ загружается.

7.5 Laplace Equation in Cylindrical Polar Coordinates 179
and
K
o
(x) = −I
o
ln
γ
x
2
+
x
2
2
2
+
x
4
2
4
. (2!)
2
1+
1
2
+
x
6
2
6
. (3!)
2
1+
1
2
+
1
3
+ .....
. (7.149)
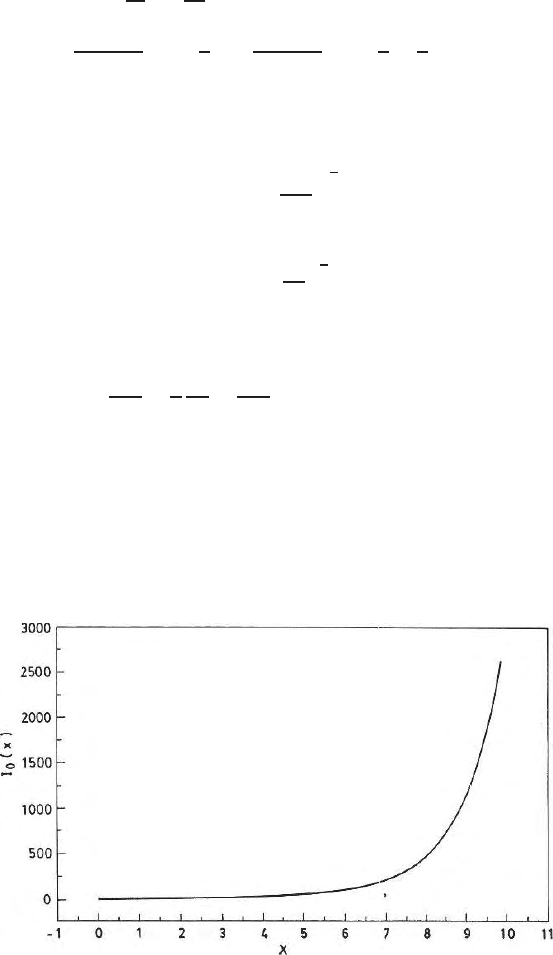
Figures 7.13 and 7.14 show the b ehaviours of I
o
and K
o
with x. At larger
distances from the source, one can write
I
n
(x) =
1
2πx
1
2
e
x
(7.150a)
and
K
n
(x) =
π
2x
1
2
e
−x
(7.150b)
as x →∞.
The g eneral solution of Laplace equation
∂
2
φ
∂ρ
2
+
1
ρ
∂φ
∂ρ
+
∂
2
φ
∂z
2
=0 forφ =f(ρ, z) (7.151)
i.e. when potential is independent of ψ, the azimuthal angle, the expression
for the potentials using Bessels functions and modified
Bessel’s functions are
φ =
∞
1
Ae
mz
+Be
−mz
[CJ
0
(mρ)+DY
0
(mρ)] (7.152)
Fig. 7.13. Modified Bessel’s function of the first kind and of zero order I
0
and its
variation with x
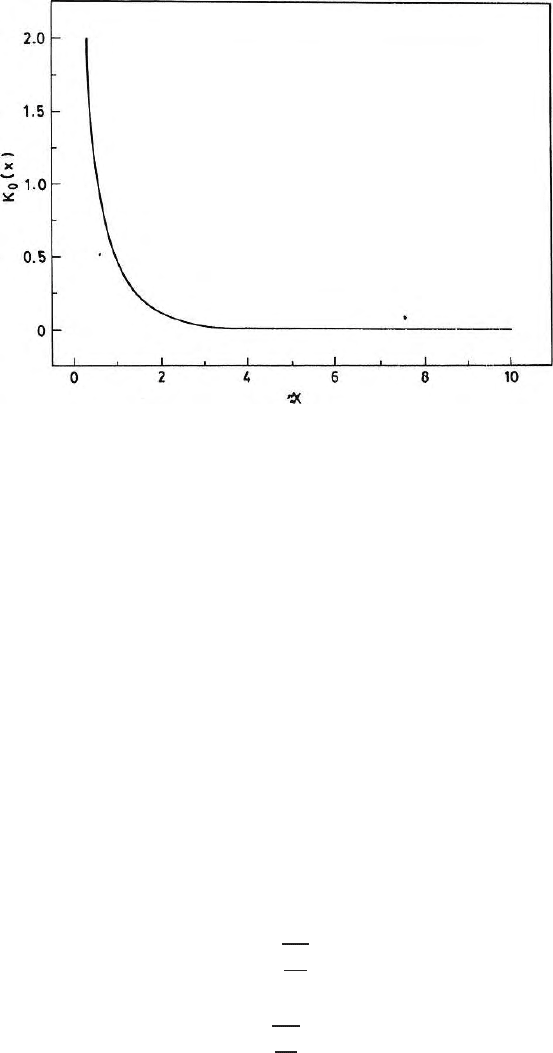
180 7 Solution of Laplace Equation
Fig. 7.14. Variation of modified Bessel’s function of the second kind and zero order
with x
or,
φ =
∞
1
(A cos mz + B sin mz) [CI
0
(mρ)+DK
0
(mρ)]. (7.153)
Instead of taking the potential functions in the form of A cos mz, B sin mz, we
can always express the potential functions in the complex form e
imz
where the
real and imaginary parts can be separated. We now define two new functions
of the form
H
1
0
(mρ)=J
0
(mρ)+i Y(mρ)
and
H
2
0
(mρ)=J
0
(mρ) −iY(mρ) (7.154)
This two functions are called Henkel’s functions of the first and second kind.
Henkel’s functions are also the potential functions and the general solution
for the Laplace equation in cylindrical co-ordinates can also be written as
Φ=
Ae
mz
+Be
−mz
'
CH
1
0
(mρ)+DH
2
0
(mρ)
(
(7.155)
Here
H
(1)
0
(x)
x→∞
=
0
2
πx
e
i(x−π/4)
and
H
(2)
0
(x)
x→∞
=
0
2
πx
e
−i(x−π/4)
. (7.156)
7.5 Laplace Equation in Cylindrical Polar Coordinates 181
We find that as
ρ → 0, J
0
→ 1, Y
0
→∞,I
0
→ 1, K
0
→∞and H
0
→∞.Andforρ →∞,
J
0
→ 0, Y
0
→ 0. I
0
→∞,K→ 0andH
0
→ 0. Therefore, remembering
the behaviours of these Bessel’s fu n ction we have to choose the proper poten-
tial function dictated by the nature of the boundary value problems. Bessels
function of the first kind are generally used. However in problems where mod-
ified Bessel’s function are needed both first and second kind of are used in
the geophysical problems as will be shown in the later chapters. Bessels func-
tions of imaginary and fractional orders are also used in solving geophysical
problems(see Chap. 8 and 13).
7.5.8 Some Relation of Bessel’s Function
From
J
n
(x) =
α
s=0
(−1)
s
x
2
n+2s
Π(s)Π(n+s)
(7.157)
we get, taking J
/
n
(x) =
d
dx
J
n
(x),
xJ
/
n
(x) =
α
s=0
(−1)
s
(n + 2S)
Π(s)Π(n+s)
.
x
2
n+2s
(7.158)
=nJ
n
+x
α
s=1
(−1)
s
Π(s− 1) Π (n + s)
.
x
2
n+2s−1
. (7.159)
If in (7.159), we put S = r + 1, we obtain
xJ
/
n
=nJ
n
− x
α
r=0
(−1)
r
Π(r)Π(n+1+r)
x
2
n+r+1
(7.160)
=nJ
n
− xJ
n+1
. (7.161)
In the same way we can prove that
xJ
/
n
+nJ
n
=xJ
n−1
. (7.162)
If we add (7.161) and (7.162) and get
2J
/
n
=J
n−1
− J
n+1
. (7.163)
If we put n = 0, we have
J
/
0
= −J
1
. (7.164)
If we multiply (7.162) by x
−n−1
,weget
x
−n
J
/
n
=x
−n−1
nJ
n
− x
−n
J
n+1
. (7.165)
182 7 Solution of Laplace Equation
Hence
d
dx
x
−n
J
n
= −x
−n
J
n+1
. (7.166)
Similarly, it can be proved that
d
dx
(x
n
J
n
)=x
n
J
n−1
. (7.167)
If we substract (7.165) from (7.162), we g et
2J
n
x
=J
n−1
+J
n+1
. (7.168)
Expression for J
n
(x) when n is half and odd integer will be as follows.
If we put n =
1
2
, in the general series for J
n
(x), we obtain
J
1
2
(x) =
α
s=0
(−1)
5
Π(s)Π
s+
1
2
x
2
2s+
1
2
. (7.169)
Since
Π(r)= rΠ(r− 1)
and
Π(s) = S, if S = 1, 2, 3.
We have
Π
1
2
=
√
π
2
and
sin x
x
=
1 −
x
2
3!
+
x
4
5!
− ..........
.
Hence
J
1
2
(x) =
0
2
πx
sin x. (7.170)
if
n=−
1
2
, J
−
1
2
(x) =
0
2
πx
cos x. (7.171)
From the recurrence formulae, we get for n =
1
2
1
x
J
1
2
(x) = J
−
1
2
(x) + J
3
2
(x)
J
3
2
(x) =
1
x
J
1
2
(x) − J
−
1
2
(x) (7.172)
=
0
2
πx
sin x
x
− cos x
. (7.173)

7.6 Solution of Laplace Equation in Spherical Polar Co-ordinates 183
7.6 Solution of Laplace Equation in Spherical Polar
Co-ordinates
Lapalce equation ∇
2
φ = 0 in spherical polar co-ordinates where φ =f(r, θ, Ψ)
is given by (Fig. 7.15)
∇
2
φ =
∂
∂r
r
2
∂φ
∂r
+
1
sin θ
∂
∂θ
sin θ
∂φ
∂θ
+
1
sin
2
θ
∂
2
φ
∂ψ
2
= 0 (7.174)
This equation can be solved applying the method of separation of variable
choosing
φ = R(r)Θ(θ)Ψ(ψ)
where R, Θ and Ψ are respectively the functions of r, θ and ψ only.
7.6.1 When Potential is a Function of Radial Distance r i.e.,
φ =f(r)
When potential is a function of r i.e., φ = f(r) only and is independent of θ
and Ψ. The Laplace equation reduces to
∂
∂r
r
2
∂φ
∂r
= 0 (7.175)
⇒ r
2
∂φ
∂r
=C
1
where C
1
is a constant. (7.176)
From the (7.176), we can get
φ =C
2
−
C
1
r
(7.177)
where C
2
is another constant. This is the potential at a point at a distance r
from the source due to a point source of current. Since the potential will be
zero at r = ∞. Therefore C
2
= 0, and the potential reduces to
Fig. 7.15. Spherical polar coordinate

184 7 Solution of Laplace Equation
φ = −
C
1
r
(7.178)
Since
E=−gradφ = −
C
1
r
2
and I =
J.n .ds
=
σ
E.n.ds = −σ
C
1
r
2
.
ds = −σ
C
1
r
2
4πr
2
= −4πσC
1
. Hence C
1
= −
I
4πσ
and
φ =
I
4πσ
,
1
r
=
Iρ
4π
. =
1
r
. (7.179)
where ρ is the resistivity of the medium and ρ=
.
1
σ
.
This is the expression for potential at a point at a distance ‘r’ from a point
source in an homogeneous and isotropic full spa ce. The solid ang le subtended
at the source point is 4π. For an air-earth boundary, when the point electrode
is on the surface the potential at a point at a distance ‘r’ from a point source
is
φ =
Iρ
2π
.
1
r
(7.180)
where the solid angle subtended at a point source is 2π on the surface of a
homogeneous and isotropic half space.
7.6.2 When Potential is a Function of Polar Angle, i.e., φ =f(θ)
When potential is independent of r and Ψ and is a function of θ only (Fig. 7.15)
the Laplace equation reduces to
1
sin θ
.
∂
∂θ
sin θ −
∂φ
∂θ
=0. (7.181)
From (7.181), we get
sin θ
∂φ
∂θ
=C
2
. (7.182)
Integrating (7.182), we get
φ =C
1
+C
2
ln tan
θ
2
(7.183)
Here the equipotentials form cones at the centre.
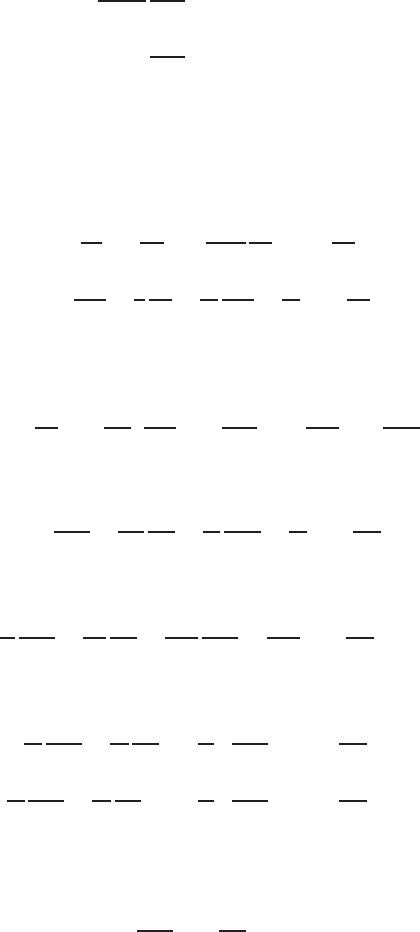
7.6 Solution of Laplace Equation in Spherical Polar Co-ordinates 185
7.6.3 When Potential is a Function of Azimuthal Angle i.e.,
ϕ =f(ψ)
Here potential is a function of Ψ only, the Laplace equation is
1
Sin
2
θ
∂
2
φ
∂ψ
2
=0
=>
∂
2
φ
∂ψ
2
=0orφ =A+Bψ. (7.184)
7.6.4 When Potential is a Function of Both the Radial Distance
and Polar Angle i.e., φ =f(r, θ)
And is independent of the azimuthal angle, the Laplace equation is
∂
∂r
r
2
∂φ
∂r
+
1
sin θ
∂
∂θ
sin θ
∂φ
∂θ
= 0 (7.185)
⇒
∂
2
φ
∂r
2
+
2
r
∂φ
∂r
+
1
r
2
∂
2
φ
∂θ
2
+
1
r
2
cot θ
∂φ
∂θ
=0. (7.186)
Now applying the method of separation of variables, we get φ(r, θ)=R(r)Θ(θ)
where R and Θ are functions of r and θ only. We have
∂φ
∂r
=Θ
dR
dr
;
∂
2
φ
∂r
2
=Θ
d
2
R
dr
2
and
∂
2
φ
∂θ
2
=R
d
2
Θ
dθ
2
.
Substituting these values in the Laplace equation, we get
Θ
d
2
R
dr
2
+
2Θ
r
dR
dr
+
R
r
2
d
2
Θ
dθ
2
+
R
r
2
Cotθ
dΘ
dθ
=0. (7.187)
Dividing (7.187) by R and
Θ
1
R
d
2
R
dr
2
+
2
rR
dR
dr
+
1
r
2
Θ
d
2
Θ
dθ
2
+
1
r
2
Θ
Cotθ
dΘ
dθ
=0. (7.188)
Equation (7.188) can be rewritten as
r
2
R
d
2
R
dr
2
+
2r
R
dR
dr
+
1
Θ
d
2
Θ
dθ
2
+Cotθ
dΘ
dθ
= 0 (7.189)
⇒
r
2
R
d
2
R
dr
2
+
2r
R
dR
dr
= −
1
Θ
d
2
Θ
dθ
2
+Cotθ
dΘ
dθ
=n
2
. (7.190)
These two independent equations are f u nction of r and θ respectively and are
equal. They are written as
r
2
d
2
R
dr
2
+2r
dR
dr
− n
2
R = 0 (7.191)
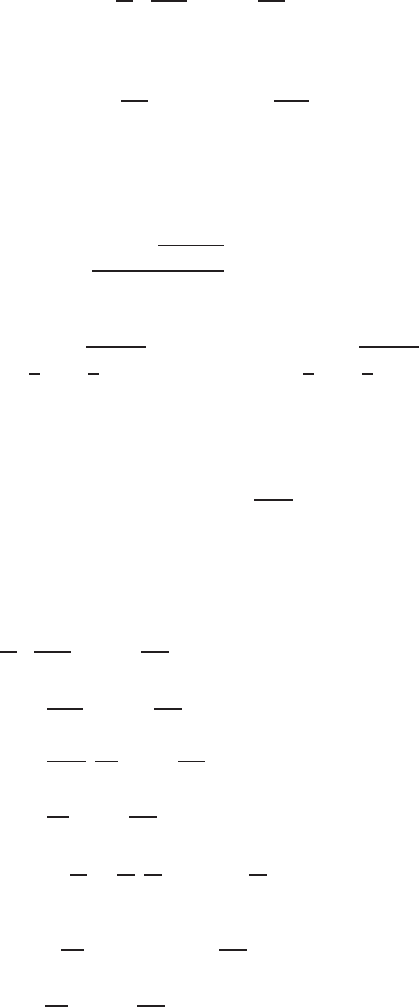
186 7 Solution of Laplace Equation
and
−
1
Θ
d
2
Θ
dθ
2
+Cotθ
dΘ
dθ
=n
2
. (7.192)
For solving (7.191), we take
R(r)=r
α
, then
dR
dr
= αr
α−1
and
d
2
R
dr
2
= α (α − 1) r
α−2
.
Substituting these values in (7.191), we get
r
2
'
α (α −1) + r
α−2
(
+2r
'
αr
α−1
(
− n
2
r
α
=0. (7.193)
⇒ α (α − 1) 2α − n
2
=0⇒ α
2
+ α − n
2
=0
⇒ α =
−1 ±
√
1+4n
2
2
.
Therefore, the two roots a re
α
1
= −
1
2
+
0
1
4
+n
2
and α
2
= −
1
2
−
0
1
4
+n
2
. (7.194)
If α
1
= α,thenα
2
= −(α + 1), therefore the two solution are R(r) = r
α
and
r
−(α+1)
taking α = n, the general solution of the first equation is
R=
Ar
n
+
B
r
n+1
(7.195)
where A and B are arbitrary constants to be determined from the boundary
conditions.
The second differential equation is
−
1
Θ
d
2
Θ
dθ
2
+Cotθ
dΘ
dθ
= (n + 1) (7.196)
⇒
d
2
Θ
dθ
2
+Cotθ
dΘ
dθ
+n(n+1)Θ=0
⇒
1
sin θ
.
d
dθ
sin θ
dΘ
dθ
+sinθ.n(n + 1)Θ = 0 (7.197)
⇒
d
dθ
sin θ
dΘ
dθ
+sinθ.n(n + 1)Θ = 0.
Let µ =cosθ,Then
d
dθ
=
d
dµ
.
dµ
dθ
= −Sin θ
d
dµ
Substituting, these values
− sin θ
d
dµ
sin θ (−sin θ)
dΘ
dµ
+sinθn(n+1)Θ=0
=
d
dµ
sin
2
θ
dΘ
dµ
+n(n+1)=0. (7.198)

7.6 Solution of Laplace Equation in Spherical Polar Co-ordinates 187
Since sin θ =
1 −µ
2
, (7.199) changes to the form
d
dµ
1 −µ
2
dΘ
dµ
+ n (n + 1) Θ = 0 (7.199)
⇒
1 −µ
2
d
2
Θ
dµ
2
− 2µ
dΘ
dµ
2
+n(n+1)Θ=0. (7.200)
This is termed as the Legendre’s differential equations. It is written as
1 − x
2
d
2
y
dx
2
− 2x
dy
dx
+n(n+1)y=0. (7.201)
7.6.5 Legender’s Equation and Legender’s polynomial
To solve the (7.201), we use Frobeneous power series and put
Y=a
0
+a
1
x+a
2
x
2
+
=Σa
s
x
s
. (7.202)
Substituting this value of Y in (7.202), we get
Σa
s
s(s− 1) x
s−2
− Σa
s
s(s− 1) x
s
− Σ2a
s
sx
s
+Σn(n+1)a
s
x
s
= 0 (7.203)
⇒ Σa
s
s(s− 1) x
s−2
+Σ[n(n+1)− s(s+1)]a
s
x
s
=0. (7.204)
If we put S = 2 and equate the co-efficients of x
0
,weget
a
2
= −
n(n+1)
2
a
0
. (7.205)
Equating the co-efficient of x
1
,weget
a
3
= −
(n − 1) (n +2)
2.3
.a
1
. (7.206)
Equating the Co efficient of x
2
,weget
a
4
= −
'
n
2
+n− 6
(
a
2
3.4
=
(n − 2) (n + 3)
3.4
n(n+1)
2
a
0
⇒
(n − 2) (n + 3) (n + 1) (n)
2.3.4.
a
0
. (7.207)
Here a
0
and a
1
are two arbitrary constants is terms of which we can collect
the terms and present in the following way
188 7 Solution of Laplace Equation
y=a
0
1 −
n(n+1)
∠2
x
2
+
n(n− 2) (n + 1) (n + 3)
∠4
x
4
− ..............
+a
1
x
1 −
(n − 1) (n + 2)
∠3
x
2
+
(n −1) (n + 2) (n − 3) (n + 4)
∠5
x
4
− .....
.
(7.208)
Till now we have not made any restriction on ‘n’ . But for most of the physical
problems, n is an integer. When n is even, i.e. 0, 2, 4, .............. the first
series terminates after a few terms. When n is odd the second series terminates
after a few terms. Therefore, we get one polyno mial and one infinite series.
For n = 0,
y
0
=a
0
+a
1
x
1+
x
2
3
+
x
4
5
+ ......
(7.209)
For n = 1
y
1
=a
1
x+a
0
1 −x
2
−
x
4
3
−
x
6
5
− ......
(7.210)
For n = 2
y
2
=a
0
1 −3x
2
+a
1
x
1 −
2
3
x
2
−
x
4
5
−
4x
6
35
+ ......
(7.211)
Therefore the general solution must be constituted of an infinite series and a
polynomial. If we take the polynomial part, we can write
y
0
=a
0
, y
1
=a
1
x, y
2
=a
2
1 −3x
2
, y
3
=a
1
x
1 −
5x
2
3
. (7.212)
The polynomial part of the solution can be written as
Y
0
=1=P
0
(x) , Y
1
=x=P
1
(x) , Y
2
=
1
2
3x
2
− 1
=P
2
(x)
Y
3
=
1
2
3x
3
− 3x
2
=P
3
(x) . (7.213)
These polynomials are known as the Legendre’s polynomial (Fig. 7.16). These
polynomials are termed as the Legendre’s function’s of the first kind. The
infinite series is the Legendre’s function of the second kind and is denoted by
Q.
When
n=0, Q
0
(x) = tan h
−1
x=
1
2
ln
1+x
1 −x
.
When
n=1, Q
1
(x) = x Q
0
(x) − 1.
When
n=2, Q
2
(x) = P
2
(x) Q
0
(x) −
3
2
x.
