Roy K.K. Potential theory in applied geophysics

Подождите немного. Документ загружается.

7.6 Solution of Laplace Equation in Spherical Polar Co-ordinates 199

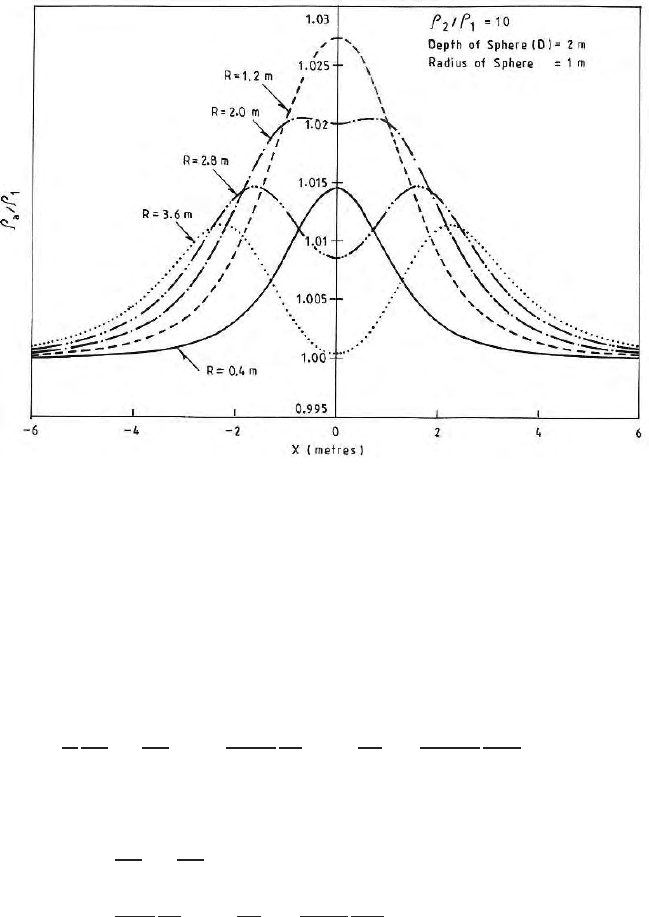
Fig. 7.21. Two electrode apparent resistivity anomaly on the surface due to a buried

spherical inhomogeneity

φ = R(r)Θ(θ)Ψ(ψ) (7.261)

It can be rewritten as

φ = R(r)S(θ, ψ). (7.262)

Keeping the surface components together. Equation (7.174) changes to the

form



= −

SSinθ

∂

∂θ



Sinθ

∂S

∂θ

−

SSin

∂

∂Ψ

. (7.263)

Equation (7.174) breaks into two parts as discussed earlier



− Rn(n + 1) = 0 (7.264)

Sinθ

∂

∂θ



Sinθ

∂S

∂θ

Sin

∂

∂φ

+ Sn(n + 1) = 0. (7.265)

The solutions of (7.191) are in the form r

and r

−(n+1)

as discussed earlier.

Now

S(θ, Ψ) = Θ(θ)Ψ

(ψ)

. (7.266)

Therefore (7.263) can be rewritten in the form

200 7 Solution of Laplace Equation

Sinθ

dθ



Sinθ

∂Θ

dθ

+Sin

θn(n + 1) = −

dψ

. (7.267)

Both sides of this (7.267) are equated to a constant m

. We get two diﬀerential

equations as follows :

dψ

ψ =0. (7.268)

and

dθ



Sinθ

dΘ

dθ

+Θ



n(n + 1)Sinθ −



Sinθ



= 0 (7.269)

The solutions of (7.268) are sin mΨ and cos mψ.

Equation (7.269) is termed as the Associated Legandre’s equation. The

solution of this equation are P

(Cos θ)andQ

(Cos θ). Here P

(Cos θ)and

(Cos θ) are known as the Associated Legendre’s function of the ﬁr st kind

and second kind. It has already been mentioned that Q

(Cos θ) is an inﬁnite

series and is generally not considered for solution of any kind of potential

problem. Therefore, the most general solution of Laplace equation in spherical

polar coordinate is

φ(r, θ, Ψ) =

∞



n=0



m=0



n+1



Cos mψ +D

Sin mψ)

(Cosθ) (7.270)

This series expansion of the general solution of the Laplace equation in spheri-

cal polar coordinate is termed as spherical harmonic expansion as discussed in

the next section. Here n is the degree and m is the order of the Associated Leg-

endre’s polynomial. When m = 0, Associated Legendre Polynomial changes to

Legendre Polynomial. The coeﬃcients A

, B

, C

, D

, are generally deter-

mined either from detailed spherical harmonic analysis or by applying suitable

boundary conditions depending upon the nature of the problem.

7.6.7 Associated Legendre Polynomial

If a Legendre Polynomial in spherical polar coordinate depends both on colat-

itude and longitude, the polynomial is termed as Associated Legendre Polyno-

mial. Associated Legendre Polynomial is denoted by P

(θ)orP

, m(θ)where

n is the degree and m is the order of the polynomial. If we diﬀerentiate the

Legendre equation

(1 −x

)

− 2x

+ n(n + 1)y = 0 (7.271)

m times, with respect to x, we get

(1 −x

)

− 2x(m + 1)

dξ

+(n−m)(n+m+1)ξ = 0 (7.272)

7.7 Spherical Harmonics 201

where

ξ =

(x)

(7.273)

If we take

η = ξ(1 − x

)

m/2

then it can be shown that (7.272) changes to the form

(1 −x

)

− 2x

dη



n(n + 1) −

1 −x

η = 0 (7.274)

This is the Associated Legendre equation. It is observed that

η =(1− x

)

m/2

(x) (7.275)

This η is the Associated Legendre Polynomial and is denoted by P

(x) or

(θ). Therefore

(x) = (1 −x

)

m/2

(x). (7.276)

7.7 Spherical Harmonics

A function is said to be harmonic if the function and its ﬁrst derivative are

continuous within the domain and it satisﬁes Laplace equation ∇

φ =0.Many

such functions exist which satisfy these conditions a nd many of those functions

can b e expressed in series forms. Harmonic functions which satisfy Laplace

equation in spherical polar coor d in ates (r, θ, ψ) are called spherical harmonics

where the potential function is dependent upon the radial direction, latitude

or colatitude and longitude or the azimuthal direction. Harmonics which are

functions of r, θ, ψ are called spherical solid harmonics in a three dimensional

space. Harmonics on the surface, which are function of θ and ψ are called

spherical surface harmonics. If φ is a spherical harmonics of degree n, then it

satisﬁes the following two conditions

∂

∂x

∂

∂y

∂

∂z

= 0 (7.277)

and

∂φ

∂x

∂φ

∂y

∂φ

∂z

=nφ. (7.278)

A spherical surface har monics is the set of values of solid spherical harmon-

ics takes on the surface of unit radius with its origin at the centre. Equa-

tion (7.174) is the Laplace equation in spherical polar co ordinate. Now if the

potential φ =H

where H

is the solid spherical harmo n ics and S

is the surface spherical harmonics. S

is a function of φ and Ψ alone and of

202 7 Solution of Laplace Equation

degree n. From (7.264) and (7.265). it can be shown that ‘r’ dependence part

of the Laplace equation can be written in the form

∂

(rΨ)

∂r

∂

n+1

)

∂r

= n(n + 1)r

(7.279)

After removing the r

part, the radial component, the surface component of

the Laplace equation in spherical coordinate changes to the form.

Sin

∂

∂θ

Sinψ

∂

∂ψ

(Sinψ

∂S

∂ψ

)+n(n+1)S

=0. (7.280)

Every spherical surface harmonics of degree n satisﬁes this equation and every

solution of this equation is a surface harmonics o f degree n (Macmillan, 1958).

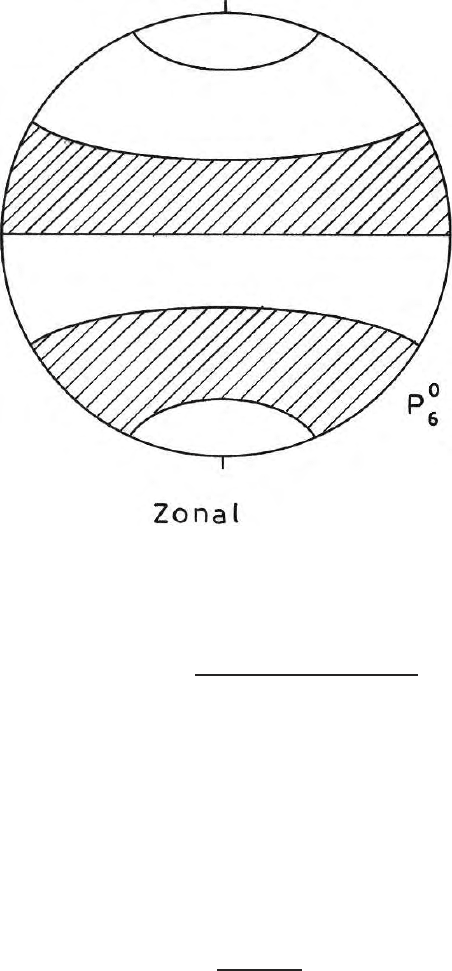
7.7.1 Zonal, Sectoral and Tess eral Harmonics

A spherical harmonic which can be expressed as a function of r and θ and

independent of Ψ the longitude, is a zonal harmonic (Fig. 7.22). Legendre

polynomials P

(θ) of degree n are independent of Ψ and are zonal harmonics.

The guiding equation for zonal harmonics is

(1 − µ

)

dµ

− 2µ

dµ

+n(n+1)P

= 0 (7.281)

The zonal harmonics from degree 0 to 6 in the form suitable for hand compu-

tations are given as

= µ

−

.µ

−

(7.282)

.µ

−

.µ

−

.µ

−

A few p oints about zonal harmonics are :

(a) Zonal harmonics are orthogonal (Fig. 7.17)

(b) Zeros of zonal harmonics are real and they all lie between 0 a nd 1.

n+1

− 2µP

′

n+1

(7.283)

where primed P

′

is the ﬁrst derivative of P.

7.7 Spherical Harmonics 203

Fig. 7.22. Nature of the zonal harmonics

(d) The general formula for Legendre p olynomial or zonal harmonics is

(Cosθ)=



J=0

(−1)

(2n − 2J − 1)

[n − 2j][n − 2j − 1][2j]

n−2j

(7.284)

(e) Legendre polynomial or zonal harmonics are better potential functions.

(f) On the surface, P

vanishes along the n circles of latitude θ.Oneofwhich

is the equator.

Legendre polynomial is used for analysing a set of data collected on the

surface of a spherical earth when the function is depen dent only on the latitude

or colatitude. If the surface harmon i cs is dependent both on θ and ψ,then

more powerful orthogonal polynomials are used. They are Associated Legendre

Polynomial and can be denoted by

n,m

(θ)=Sin

∂

∂(Cosθ)

(Cosθ) (7.285)

where m is the degree and n is the order of the Legendre Polynomial. Asso-

ciated Legendre polynomials are more powerful in the sense that Legendre

Polynomial is only a special case of Associated Legendre Polynomial. Because

204 7 Solution of Laplace Equation

when m, the order is zero, i.e., when the dependence on longitude van ishes

ALP changes to LP as mentioned.

The general solution of surface harmonics is

φ(θ, ψ)=

∞



m=0

∞



n=0



n,m

Cos mψ +D

n,m

Sin mψ



n,m

(θ)



(7.286)

The surface harmonics φ(θ, Ψ) is represented by an inﬁnite sum of Asso-

ciated Legendre Polynomials, sines and cosines. Here P

n,m

(θ)Cos mΨ and

n,m

(θ)Sin mψ are the components of the surface spherical harmonics. If

m = 0, the surface harmonics depends only on the colatitude and is called

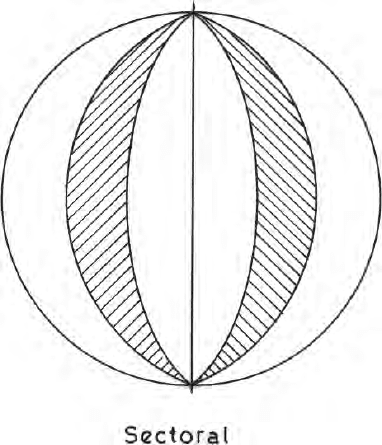
a zonal harmonics as mentioned already. If n = m, it dep ends on the longi-

tude ψ, it is then termed as the sectoral harmonics. If m > 0andn> m,

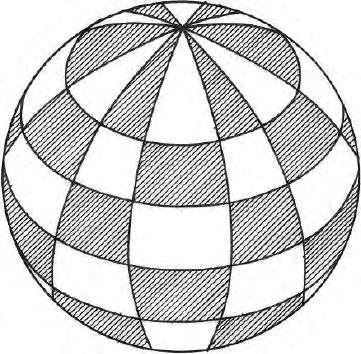
then the harmonics is termed as tesseral harmonics(Figs. 7.23, 7.24).Tesseral

harmonics are those which becomes zero both in latitude and longitude. In a

spherical polar coordinate system we express the har monic function of degree

nororderkas

φ(θ, ψ)=r

ikθ

, Sin

ψP

(7.287)

where P

is the Legendre Polynomial of degree n, and order k, Sin

Ψshows

the longitudinal dependence, e

ikθ

is the dependence on colatitude and r

the radial dependence part. If we remove r

, the surface harmonics part can

be written as

φ(θ, ψ)=e

ikθ

Sin

ψP

. (7.288)

Fig. 7.23. Nature of the sectoral harmonics

7.7 Spherical Harmonics 205

Fig. 7.24. Nature of the tesseral harmonics

The real and imaginary parts of (7.288) is given by

Real part of φ(θ, ψ)=Sin

ψP

Cos kθ

Imaginary part of φ(θ, ψ)=Sin

ψP

Sin kθ



(7.289)

These real a nd imaginary parts are the two Tesseral harmonics.

Fairly detailed description on the procedures for determining the spheri-

cal harmonic components are available in Blakely (1996). Materials for fur-

ther studies on spherical harmonics are available in Macmillan (1958), Kellog

(1953) and Ramsay (1940).

Direct Current Field Related

Potential Problems

In this chapter the basic nature of DC resistivity boundary value problems

mostly in one dimensional domain are demonstrated. Nature of the surface

and subsurface kernels for an N-layered earth in DC ﬁeld domain, nature of

boundary value problem with cylindrical symmetry needed in borehole geo-

physics, nature of boundary value problems where resistivity or conductivity

varies continuously along the vertical or horizontal direction in the presence of

both Laplacian and nonlaplacian terms are discussed. The last two problems

are on the potential problems for dipping contacts and layered aniso tropic

beds.

8.1 Layered Earth Problem in a Direct Current Domain

Direct current ﬁeld related potentials in a layered earth model can be eval-

uated as follows. Figure 8.1 shows the geometry of the problem. We assume

the earth to be horizontally layered and the number of layers is N. ρ

, ρ

,........ρ

, are the resistivities of the ﬁrst, second, third and Nth layer

and h

are their corr e spo nd ing thicknesses. Thickness of the last layer

is assumed to be inﬁnity. Potential at a point due to a point source of Current

I will have cylindrical symmetry, over a layered earth therefore, the Laplace

equation in cylindrical coordinates are chosen. Since potential is independent

of the azimuthal angle, therefore, the Laplace equation in cylindrical coord i-

nates reduce down to

∂

∂r

∂φ

∂r

∂

∂z

=0 (8.1)

and the general solution of the equation from (7.153) is

φ =

∞





A(m)e

−mz

+B(m)e



(mr) dm. (8.2)

208 8 Direct Current Field Related Potential Problems

Current Electrode Potential Electrode

Fig. 8.1. N – Layered earth model

The potential at a point due to a point source at a distance r from the point

source of Current I on the surface of the earth (from 7.181) is given by

Iρ

2π

. (8.3)

While dealing with the air earth boundary, we often use the term half space

problem because the electrical resistivity o f the air is inﬁnity. The earth has

ﬁnite re sistivi ty. The solid angle subtended at the current source is 2π.For

surface geophysics, when measurements are taken on the surface of the earth,

Iρ

2π

becomes the multiplication factor. In well logging or borehole geophysics

when electrode is placed inside a borehole, potential at a point at a distance

r from the source is

Iρ

4π

as shown in the next section. Equation (7.180).

For surface geophysics, the potential due to a point source on the surface

of an N-layered earth is

Iρ

2π

)

1/2

(8.4)

where r and z are respectively the radial and vertical distances from the source

and R =

√

. Potentials in the diﬀerent layers can, therefore, be written

= φ

+ φ

′

= φ

+ φ

′

....................

= φ

+ φ

= φ

+ φ

′

where φ

is the source potential and φ

′

, φ

′

, φ

′

.....φ

′

are the perturbation

potentials in diﬀerent media. Potential at the i

media can be written as