Roy K.K. Potential theory in applied geophysics

Подождите немного. Документ загружается.

8.2 Potential due to a P oint Source in a Borehole 229

Since

2π

∞



(m) K

(mr) cos mz dm (8.107)

∂φ

∂r

2π

∞



(m) K

(mr) m cos mz dm

= −

2π

∞



(m) K

(mr) m cos mz dm. (8.108)

Using the boundary conditions, i.e., at r = r

∂φ

∂r

∂φ

∂r

,weget

∞



(m) I

(mr

) −K

(mr

)] cos mz.m.dm

∞



(m) I

(mr

)+D

(m) K

(mr

)] m cos mz dm (8.109)

⇒ C

(m) I

(mr

) − K

(mr

) −C

(m) I

(mr

)+D

(m) K

(mr

)=0.

Similarly at

r=r

∂φ

∂r

∂φ

∂r

hence

∞



(m) I (mr

) −D

(m) K

(mr

)}cos mz m dm

= −

∞



(m) K

(mr

)cosmz m dm

⇒ C

(m) I

(mr

) −D

(m) K

(mr

)+D

(m) K

(mr

)=0. (8.110)

The four simultaneous equations with four unknowns are given by

(m) I

(mr

)+ρ

(mr

) −ρ

(mr

(m) −ρ

(m) K

(mr

)=0

(8.111)

(m) I

(mr

)+ρ

(m) K

(mr

) −ρ

(m) K

(mr

) = 0 (8.112)

(m) I

(mr

) −K

(mr

) −C

(m) I

(mr

)+D

(m) K

(mr

) = 0 (8.113)

(m) I

(mr

) −D

(m) K

(mr

)+D

(m) K

(mr

)=0. (8.114)

230 8 Direct Current Field Related Potential Problems

In borehole geophysics, we are mostly interested to ﬁnd out potential on axis

of the b orehole, i.e. in medium 1. Therefore for computation of p otential

in borehole, we need to evaluate the kernel C

(m) only. However the other

kernels C

(m), D

(m) and D

(m) which are of academic interest in Potential

Theory can also be evaluated from these sets of equations. Equations 8.111,

8.112, 8.113 and 8.114 can be rewritten in the matrix form and

(m) can be evaluated using Cramer’s rule.

Let

(m) =

∆

where

⎡

⎢

⎣

−ρ

(mr) −ρ

(mr) − ρ

(mr) 0

0 ρ

(mr

) ρ

(mr

) −ρ

(mr

)

(mr) −I

(mr) K

(mr

) −K

(mr

)

⎤

⎥

⎦

. (8.115)

Determinant of the numerator N of C

(m) is

N=(ρ

− ρ

)(ρ

− ρ

(mr

)[I

(mr

)

−I

(mr

)] + (ρ

− ρ

) ρ

(mr

)

(ρ

− ρ

) ρ

(mr

(mr) . (8.116)

The denominator ∆ is given by

∆=

⎡

⎢

⎣

(mr

) −ρ

(mr

) −ρ

(mr) 0

0 ρ

(mr

) ρ

(mr

) −ρ

(mr

)

(mr

) −I

(mr

) −K

(mr

)

⎤

⎥

⎦

. (8.117)

After a few steps algebraic simpliﬁcation while calculating the determinant

from (8.117), we get.

∆=[I

(mr

)+I

(mr

)]

+[I

(mr

) K

(mr

)+(μ

− 1) (μ

− 1) (mr

)]

+I(mr

(mr

)+(mr

)(µ

− 1)

(mr

)(mr

)(µ

− 1) + 1 (8.118)

where µ

and µ

.ThusthevalueofCo(m)=N/∆canbe

computed.

The expression for the potential in a borehole is given by

2π

⎡

⎣

∞



(mr) cos mz dm +

∞



(m) I

(mr) cos mz dm

⎤

⎦

. (8.119)

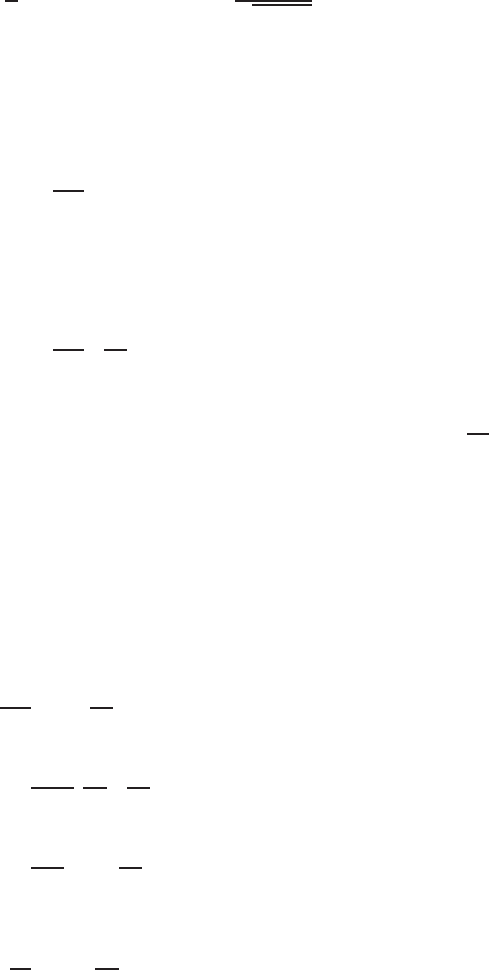
8.2 Potential due to a P oint Source in a Borehole 231

From Weber – Lipschitz integral, we get

∞



(mr) cos mz dm =

√

. (8.120)

At any point on the z axis where r = 0, we get

(mr) = I

(0) = 1.

Therefore,

r=0

2π

⎡

⎣

∞



(mr) cos mz dm

∞



(m) I

(mr) cos mz dm

2π

⎡

⎣

∞



(m) cos mz dm

⎤

⎦

. (8.121)

This is the expression for potential at a point on the z axis due to a p oint

electrode. Since apparent resistivity of a medium is expressed as ρ

∆φ

where K is the geometric factor, ∆φ is the potential di ﬀerence between th e

two potential electrodes and I is the current ﬂowing through the ground. For

a two electrode conﬁguration the geometric factor K = 4πL, where L is the

electro de separation and ∆φ = φ, i.e. the potential measured at the potential

electrode M (Fig. 8.3).

The other po t ential electrode is theoretically at i nﬁnitely and practically is

at a distance about ten times the distance between the current and potential

electrodes. In practice the other electrodes are on the surface. The apparent

resistivity can be expressed as

2π

.4πL

⎡

⎣

∞



(m) cos mz dm

⎤

⎦

⇒

2ρ

⎡

⎣

∞



(m) cos mz dm

⎤

⎦

⇒

⎡

⎣

∞



(m) cos mz dm

⎤

⎦

Hence

=1+

∞



(m) cos mL dm. (8.122)

232 8 Direct Current Field Related Potential Problems

Fig. 8.3. Computed apparent resistivity curve in two electrode conﬁguration bore

hole environment

8.3 Potential for a Transitional Earth

8.3.1 Potential for a Medium Where Physical Property Varies

Continuously with Distance

This section deals with the boundary value pro b l ems where resistivity of a

medium is assumed to vary continuously with depth or radial distance. The

place where physical prop erty of the earth changes continuously with depth,

the nature of the boundary value problem changes because of the inclusion

of nonlaplacian terms. The resistivity ρ is assumed to be a function of depth

Z. There are some zones in the subsurface where resistivity varies continu-

ously with depth. As for example, in a hard rock area, weathered granite

overlies hard and compact granite. It may be a transitional zone where resis-

tivity increases continuously with depth. In a borehole the mud ﬁltrate invades

through the porous and permeable zone because of high borehole pressure and

8.3 Potential for a Transitional Earth 233

an invaded zone is formed surrounding the borehole wall. It is always a tran-

sition zone, where resistivity varies continuously along the radia l direction.

For a transitional earth ρ is either a function of z or r or both r, z. In this

section treatments for both ρ = f(z) and f(r) are given. When ρ = f(z), the

starting equation in a source free region and for an isotropic earth is

div



J=0.

⇒ div(σ grad φ)=0

⇒ σ div grad φ +gradσ grad φ =0

⇒∇

φ +

grad σ grad φ =0. (8.123)

If we take cylindrical co-ordinates with z axis downward for φ =f(r, z), (8.123)

can be written as

σ∇

φ +

∂σ

∂r

∂φ

∂r

∂σ

∂z

∂φ

∂z

=0. (8.124)

If we assume that

∂σ

∂r

= 0, i, e., the lateral variation in conductivity o r resis-

tivity is absent (8.124) changes to the form

∇

φ +

∂σ

∂z

∂φ

∂z

=0. (8.125)

Here conductivity varies continuously with depth (Fig. 8.4). Therefore, we can

write (8.125) as

∂

∂r

∂φ

∂r

∂σ

∂z

∂φ

∂z

∂

∂z

=0. (8.126)

Using the method of separation of variables, we obtain

φ = R (r)Z(z)

− m

R = 0 (8.127)

dσ

− m

Z =0. (8.128)

To solve this problem, we need to know the value of

dσ

.Letthesolution

of the second (8.128) be Z(m,z). The solution of the ﬁrst equation is J

(mr)

and Y

(mr).Since J

(mr) is a better behaved potential function at r = 0, the

expression for the potential is

φ =



A (m)Z (mz) J

(mr) dm. (8.129)

Now applying the ﬁrst boundary condition i.e.

∂φ

∂z

=0at z =0,

234 8 Direct Current Field Related Potential Problems

we get

∂φ

∂z



A(m)Z

′

(mz) J

(mr) dm (8.130)

where

′

dZ (m, z)

From this boundary condition, we can write



A(m)Z

′

(m, 0) J

(mr) dm = 0 at z = 0. (8.131)

Since



(mr)dm = 0 always from the theory of Bessel’s function, (Watson

1966), therefore

A(m)Z

′

(m, 0) = A (m) Z

′

(m, 0) = Cm.m

where Cm is a constant.

Hence

A(m) =

Cm.m

′

(m, 0)

(8.132)

and

φ (r, z) =



Cm.m

′

(m, 0)

Z(mz)J

(mr)dm



k(mz)J

(mr)dm. (8.133)

Here k(m,z) is said to be the kernel of this integral.

For a homogeneous earth of resistivity ρ

φ (r, Z) =

2π

√

Iρ

2π



−mZ

(mr) dm. (8.134)

(Weber Lipschitz identity)

−mZ

is the appropriate p otential function because potential vanishes to zero

at inﬁnite depth.

Therefore

φ (r, z) = C



−mZ

(mr) dm (8.135)

where C =

Iρ

2π

8.3 Potential for a Transitional Earth 235

Comparing this equation with the present problem, we get

φ (r, z) =

Iρ

2π



k(m, 0) J

(mr) dm (8.136)

where ρ

= ρ right at the surface.

Since in surface geophysics, we take measurements on the surface,

φ (r, 0) =

Iρ

2π

∞



k (m, 0) J

(m, r ) dm (8.137)

where

k(m, 0) =

mZ(m, 0)

′

(m, 0)

. (8.138)

Theexactvalueofφ will depend upon Z. Three such cases, are discussed in

this section.

Problem 1

Expressions for the potential when the resistivity of the earth decreases, expo-

nentially with depth (Fig. 8.4).

The (8.128) changes to the form

+ β

− m

Z = 0 (8.139)

This is a diﬀerential equation of a damped oscillatory circuit. The solution is

Z=e

−β+

√

+4 m

−β−

√

+4 m

. (8.140)

The second value of Z satisﬁes the prop er potential function, hence

Transitional Source

Fig. 8.4. A medium where electrical conductivity is varying continuously wit depth

236 8 Direct Current Field Related Potential Problems

Z(m, z) = e

−β−

√

−4m

(8.141)

′

(m, z) =

−β −



− 4m

.Z(m, z) .

Since k (m, z) =

mZ(m,z)

′

(m,z)

φ (r, 0) =



k(m, 0)J

(mr) dm (8.142)

where

k(m, o) = m

⎡

⎣

−

− m

⎤

⎦

Problem 2

When electrical condu ctivi ty of the medium varies linearly with depth

(Fig. 8.4). Let

σ = σ

+ σ

Z=σ





Here σ

is the conductivity at the surface. Therefore,

dσ

(8.143)

and (8.128) takes the form

+ σ

− m

Z = 0 (8.144)

has the unit mho/m and a has the unit of length. If we put

+ σ

Z=σ

ξ(z) (8.145)

ξ =

+ z = z + a

Then the (8.144) changes to the form

dξ

− m

Z = 0 (8.146)

This is the modiﬁed Bessel’s equation of zero order and the solutions are

(mξ)andK

(mξ). Since I

(mξ) is not an appropriate potential function

8.3 Potential for a Transitional Earth 237

because I

→∞for Z →∞,K

(mξ) is a better potential function. Therefore

the solution of the (8.146) is

Z=AK

(mξ)=AK

(m(z + a)) (8.147)

Since

k (m, 0) =

K (ma)

′

(ma)

Therefore

φ (r, 0) =

2πσ

∞



(ma)

′

(ma)

(mr ) dm. (8.148)

Put ma = λ

Then

φ (r, 0) =

Iρ

2πr

∞



(λ)

′

(a)





dλ. (8.149)

Here

is dimensionless and λ is the integration variable. For an homogeneous

earth

(r, 0) =

Iρ

2πr

Therefore

φ (r, 0)

(r, 0)

∞



(λ)

′

(λ)



λr



dλ (8.150)

Problem 3

When the electrical resistivity varies linearly with depth (Fig. 8.4)

Let

ρ = ρ

+ ρ

z=ρ

(1 + z/b) (8.151)

The equation (8.128) takes the form

−

+ ρ

− m

Z=0. (8.152)

If we put ρ

+ ρ

Z=ρ

ξ, ξ = b + z, the (8.152) changes to the form

dξ

−

dξ

− m

Z=0. (8.153)

Substituting Z = ξη,weget

dξ

dη

dξ

−





η =0. (8.154)

238 8 Direct Current Field Related Potential Problems

The solutions of this modiﬁed Bessel’s equation in mξ are I

(mξ)andK

(mξ).

Since K

(mξ) is a better potential function.

therefore

Z=C(z+b)K

[m(z + b)]. (8.155)

Where C is constant and

′

(m, 0) = K

(mb) + m bK

′

(mb)

and

φ (r, 0) =

Iρ

2π

∞



mb K

(mb)

(mb) + mb (K

′

(mb))

(mr)dm

Iρ

2π

∞



mb K

(mb)

(mr)dm. (8.156)

Here

(mb) = K

(mb) + mb K

′

(mb) (Watson, 1966)

Iρ

2π

∞



′

(mb)

(mr) dm (8.157)

Putting λ =mb,weget

φ (r, 0) =

Iρ

2πr

∞



′

(λ)





dλ. (8.158)

Problem 4 An Alternative Approach for Solution of φ (r,z)

When ρ =f(z)

When ρ the resistivity of the earth is a function of z only, the gov erning

equation in the Laplacian ﬁeld is div



J = 0. It can be written as

∇.



∇φ (r, z)

ρ (z)



=0. (8.159)

Since

div



∂J

∂x

∂J

∂y

∂J

∂z

= 0 (8.160)

we can write

∂

∂x



ρ (z)





∂

∂y



ρ (z)





∂

∂z



ρ (z)





⇒

ρ (z)



∂

∂x

∂

∂y

∂

∂z

∂

∂z



ρ (z)



∂φ

∂z

=0.