Roy K.K. Potential theory in applied geophysics
Подождите немного. Документ загружается.


8.3 Potential for a Transitional Earth 249
and
σ =
σ
t
− σ
x0
r
tr
− r
x0
.
With algebraic simplifications (taking a = a
1
/σ
t
)onegets,
d
2
R
dr
2
+
a+2r
r(a+r)
dR
dr
− m
2
R = 0 (8.214)
⇒ r
2
d
2
R
dr
2
+ar
d
2
R
dr
2
+2r
dR
dr
+a
dR
dr
− m
2
r
2
R − m
2
arR = 0
⇒ r
2
R
′′
+arR
′′
+2rR
′
+aR
′
− m
2
ar R = 0. (8.215)
Here also we assume the solution in an extended power series form, as at
r = 0 the coefficient of dR/dr is not analytic,
R=
∞
p=0
A
p
r
p+q
.
Substituting the values of R
′′
R
′
and R in the (8.214) one g ets,
∞
p=0
(p + q ) (p + q − 1) A
p
r
p+q
+a
∞
p=0
(p + q) (p + q − 1) A
p
r
(p+q−1)
+2
∞
p=0
(p + q ) A
p
r
(p+q)
+a
∞
p=0
(p + q) A
p
r
(p+q−1)
− m
2
∞
p=0
A
p
r
(p+q+2)
− am
2
∞
0
A
p
r
(p+q+1)
=0. (8.216)
Equating the coefficient of r
q−1
, taking p = 0 the above equation reduces to
aq
2
A
0
=0
As a and A
0
cannot be zero, hence q = 0. It implies that q has distinct
double roots.
Putting the value of q in (8.215) and equating the coefficient of r
p−1
,one
gets the generating expression of A
P
i.e.,
A
p
=
1
ap
2
'
m
2
A
p−3
+am
2
A
p−2
− (p − 1) pA
p−1
(
(8.217)
We can write the solutions of the differential (8.215) as, (taking q = 0)
T
1
(m, r) = r
1
=R|
q=0
T
2
(m, r) = R
2
=R
1
ln r +
∞
p=0
K
p
r
p
. (8.218)
250 8 Direct Current Field Related Potential Problems
Since the indicial equation has distinct double roots, we have two solutions o f
the differential equation. First solution is T
1
(m, r) provided we can determine
the coefficient A
p
. Second solution of differential equation is T
2
(m, r) and the
coefficient K
p
has to be determined. Generalised expression of the coe fficient
term can be found out with simple mathemat i cal steps.
From (8.215), we get
R
′
2
=R
′
1
ln r + R
1
/r+
∞
p=1
pK
p
r
p−1
(8.219)
R
′′
2
=R
′′
1
ln r + 2R
′
1
/r − R
1
/r
2
+
∞
p=0
p(p− 1) K
p
r
p−2
(8.220)
Putting these values in the differential (8.219 and 8.220) and after some math-
ematical steps, terms for K can be found out after equating the coefficients of
different powers of r.
Equating the coefficients of r
0
,r
1
,r
2
and r
3
, we respectively get
(i)
K
1
= −A
0
/a (8.221)
(ii)
K
2
= −(2K
1
+ 4aA
2
) /a
2
2
(8.222)
(iii)
K
3
=
am
2
K
1
− 6K
2
− 5A
2
− 6aA
3
/a
2
3
(8.223)
(iv)
K
4
=(m
2
K
1
+am
2
K
2
− 4(4 −1)K
3
− 7A
3
− 8aA
4
)/a4
2
. (8.224)
The generalised solution for potential of the transitional invaded zone
K
p
=(m
2
K
p−3
+am
2
K
p−2
− p(p − 1)K
p−1
− (2p − 1)A
p−1
− 2ap A
p
)/ap
2
(8.225)
(for both the models) can be written as,
φ
3
=
∞
0
[C
′
4
(m) T
1
(m, r) + C
′
5
(m) T
2
(m, r)] [F cos mz + G sin mz] dm
(8.226)
Here T
1
(m, r) and T
2
(m, r) are the two solutions of the second order dif-
ferential equation. T
1
(m, r) and T
2
(m, r) the two solutions, are entirely
different for the two different cases (i.e., R
t
> R
x0
and R
t
< R
x0
). This can
be easily verified from the (8.197) and (8.215). C
′
4
(m), C
′
5
(m), F and G are

8.3 Potential for a Transitional Earth 251
arbitrary constants generally determined applying the boundary conditions.
In this problem, the potential is independent of the sign of z therefore sin mz
term is neglected.
Equation (8.226) reduces to the form
φ
3
=
∞
0
C
4
(m)T
1
(m, r) cos mz dm +
∞
0
C
5
(m)T
2
(m, r) cos mz dm (8.227)
where C
4
(m) = C
′
4
(m)F and C
5
(m) = C
′
5
(m)G
The general expressions for the potential in different media are
φ
1
= C
∞
0
K
0
(mr )cos mz dm +
∞
0
C
1
(m)I
0
(mr )cos mz dm (8.228)
where
C=
R
m
I
2π
2
r
m
.
φ
2
=
∞
0
C
2
(m)I
0
(mr) cos mz dm +
∞
0
C
3
(m)K
0
(mr) cos mz dm (8.229)
φ
3
=
∞
0
C
4
(m)T
1
(m, r) cos mz dm +
∞
0
C
5
(m) T
2
(m, r) cos mz dm
(8.230)
φ
4
=
∞
0
C
6
(m)K
0
(mr) cos mz dm. (8.231)
Boundary conditions are as follows: (i) φ
1
= φ
2
and J
1
=J
2
at r = r
m
(ii)
φ
2
= φ
3
and J
2
=J
3
at r = r
x0
and φ
3
= φ
4
and J
3
=J
4
at r = r
tr
where
J
1
,J
2
,J
3
and J
4
are the normal component of the current densities at the
interfaces between the four different media. On both the sides of the transition
zone, R
x0
=R
tr
at r = r
x0
and R
tr
=R
t
at r = r
tr
. Therefore the boundary
conditions J
2
=J
3
and J
3
=J
4
reduce to φ
′
2
= φ
′
3
and φ
′
3
= φ
′
4
,whereφ
′
1
,
φ
′
2
, φ
′
3
and φ
′
4
are the derivatives of the potentials with respect to r at the
respective boundaries, r = r
x0
and r = r
tr
. Applying the boundary conditions
to (8.227), (8.228), (8.229), (8.230), (8.231) and arranging them in matrix
form, one gets

252 8 Direct Current Field Related Potential Problems
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
I
0
(mr
m
)I
0
(mr
m
)K
0
(mr
m
)0 0 0
0I
0
(mr
x0
)K
0
(mr
x0
)T
1
(m, r
x0
) −T
2
(m, r
x0
)0
00 0T
1
(m, r
tr
)m T
2
(m, r
tr
)K
0
(m r
tr
)
I
1
(mr
m
) /R
m
−I
1
(mr
m
) /R
x0
K
1
(mr
m
) /R
x0
000
0I
0
(mr
x0
)m −K
1
(mr
x0
)m −T
′
1
(m, r
x0
) −T
′
2
(m, r
x0
)0
00 0T
′
1
(m, r
x0
)T
′
1
(m, r
x0
)K
1
(m r
tr
)m
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
C
1
(m)
C
2
(m)
C
3
(m)
C
4
(m)
C
5
(m)
C
6
(m)
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
−CK
0
(mr
m
)
0
0
CK
1
(mr
m
) /R
0
0
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
(8.232)
using the Bessel function identity I
′
0
(x) = I
1
(x) and K
′
0
(x) = −K
1
(x)
dT
1
(m, r)
dr
=T
′
1
(m, r) ;
dT
2
(m, r)
dr
=T
′
2
(m, r) .
Above matrix can be written in the form
XC
v
= Y (8.233)
where, C
v
is the column vector of kernel functions to be determined. Since
potential is measured in the borehole, evaluation of C
1
(m) is onl y required
from (8.227).
Potential φ
1
is given by, taking mz = x
φ
1
=C
∞
0
K
0
x
z
r
cos x
dx
z
+
1
z
∞
0
C
1
x
z
I
0
x
z
r
cos x dx (8.234)
Applying the Weber Lipschitz identity, the first integral reduces to
π
2z
at r = 0
i.e., along the borehole axis. The second integral (I
2
) reduces to the form,
I
2
=
∞
0
C
1
x
z
cos x dx (8.235)
Since I
0
x
z
r
at r = 0 is 1.0. The infinite in te gral I
2
is determined using Gauss
quadrature method. The kernel function C
1
(x/z) is determined using cubic
spline interpolation.
Expression of the potential along the borehole axis reduces to the form
φ
1
=
R
m
I
2π
2
r
m
π
2z
+
1
z
.I
2
. (8.236)
The expression for the apparent resistivity (R
a
) for a two electrode system
can be written as
R
a
=4πzφ
1
/I (8.237)
(Dakhnov, 1962)

8.4 Geoelectrical Poten tial for a Dipping Interface 253
Fig. 8.7. A model of a dipping interface between the two media of resistivities
ρ
2
and ρ
1
; A (r,o,o) is the location of the current electrod e and M is t he pont of
observation
Hence the apparent resistivity for two electrode system can b e expressed
as,
R
a
R
m
=
1
r
m
+
4π
R
m
z
I
2
. (8.238)
Taking derivatives of potential expression with respect to z, one gets the
expression for a pparent resistivity for three electrode system (lateral configu-
ration) (Fig. 8.7) as
R
a
R
m
=
1
r
m
+
4π
R
m
∞
0
C
1
(x/z) x sin x dx (8.239)
In this section, an elaborate treatment on how to handle nonlaplacian terms
along with the laplacian terms in a second order differential equation is shown.
It is demonstrated that any second order differential equation, not solvable in
closed form with suitable substitution as demonstrated, can be solved using
Frobenious power series.
8.4 Geoelectrical Potential for a Dipping Interface
Dipping bed or dipping contact problem was solved by Skalskaya (1948),
Maeda (1955), Van Nostrand and Cook (1955), De Gery and Kunetz (1956),
Dakhnov (1962) and Others. Figure 8.7 show the geometry of the problem.
Here cylindrical system of coordinate (r, θ, z) was chosen. z-axis is taken along
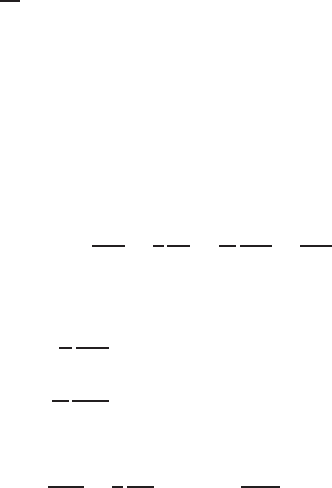
254 8 Direct Current Field Related Potential Problems
the geological strike direction,i.e., along the line of contact between two bodies
having different physical properties. Dipping contact is having a dip θ = α.
A point current electrode is placed on the surface and at the point A (r,0,0).
Because the origin is chosen at the point O(0,0,0). The Y axis is assumed ver-
tically downward from the origin O. Right hand portion of the homogenous
formation of resistivity ρ
1
is termed as the hanging wall and left portions of
the homogenous formation may b e termed as the foot wall. These are geolog-
ical terms. On the hanging wall side θ =0andonthefootwallsideθ = π
Coordinate of the point of observation M is (r, θ, z). The distances between
OandMisr,OandAisr
0
and A and M is R.Since resistivity of the air is
infinitely high,
∂φ
∂n
=0bothforθ =0andθ = π.
In Chap. 7 we have discussed two forms of the solutions of Laplace equation
in cylindrical coordinat rs in terms of Bessel’s functions and modified Bessel’s
functions. Application of both the forms are demonstrated in this chapter. In
this problem, the third form of solution of Laplace equation by the method
of separation of variables using modified Bessel’s function of imaginary order
is demonstrated.
In this problem Laplace equation is valid at all points except at the point
A. In this problem the Laplace equation is
∇
2
φ =
∂
2
φ
∂r
2
+
1
r
∂φ
∂r
+
1
r
2
∂
2
φ
∂θ
2
+
∂
2
φ
∂z
2
= 0 (8.240)
The third set of equations used in the present problem are
1
Z
d
2
Z
dz
2
= −λ
2
(8.241)
1
Θ
d
2
Θ
dθ
2
= −i
2
s
2
(i.e. n becomes i s) (8.242)
and
d
2
R
dr
2
+
1
r
dR
dr
−
λ
2
+
(is)
2
r
2
R = 0 (8.243)
The solution of this third set of equations are respectively cos λz, sin λz,
cosh sθ,sinhsθ and I
is
(λr) and K
is
(λr). I
is
(λr) and K
is
(λr) are the modified
Bessel’s function of the first and second kind and of imaginary order. In this
problem the potential is independent of the sign of z, therfore cos λz will be
the appropriate p otential function and not sin λz. When r →∞,φ→ 0. Since
I
is
(λr) approaches high values when r →∞, therefore I
is
(λr) cannot be the
proper p otential function and K
is
(λr) is the suitable potential function.
Therefore, the expression for the perturbation potential can be written as
φ =
∞
λ=0
∞
s=0
cos λzdλ (L (s, λ)cosh(sθ)+M (s, λ) sinh(sθ)K
is
(λr) ds.
(8.244)

8.4 Geoelectrical Poten tial for a Dipping Interface 255
To find the potential at M (r, θ, z), We have
φ
1
=
1ρ
1
2π
.
1
AM
. +
∞
λ=0
∞
s=0
cos λzdλ (A (s, λ)coshsθ
+ B (s, λ)sinh (sθ) K
is
(λr) ds (8.245)
φ
2
=
1ρ
1
2π
.
1
AM
. +
∞
λ=0
∞
s=0
cos λzdλ (C (s, λ)coshsθ
+D(s, λ), sin hsθ) K
is
(λr) ds. (8.246)
Now four constants in these equations can be determined applying four bound-
ary conditions, i.e.,
φ
1
= φ
2
at θ = α
1
ρ
1
∂φ
1
∂θ
=
1
ρ
2
∂φ
2
∂θ
at θ = α
∂φ
1
∂θ
=0 atθ =0
∂φ
1
∂θ
=0 atθ = π
The last two boundary conditions originate because current cannot flow across
the air-earth boundary. For this type of boundary value problems ,as has
already been discussed, one has to express the source potential in the same
format as the perturbation potential before the boundary condition is applied.
We have to express
1
AM
or
1
r
in the form of K
is
(λr). Skalskaya (1948) solved
this problem. She has shown that
1
AM
can be expressed as
1
AM
=
1
r
=
1
r
2
0
+ r
2
− 2r
0
r cos θ + z
2
=
4
π
2
∞
0
cos λzdλ
∞
0
cos hs (π − θ)K
is
(λr
0
) K
is
(λr) ds (8.247)
Let
Iρ
2π
= q. Now, applying the second set of boundary conditions
q
AM
terms
will cancel out from both the sides. Now sinh sθ = 0 and cosh sθ =1forθ =0.
Therefore, we can write down
φ
1
=
q
AM
+
∞
0
cos λzdλ
∞
0
L(S
1
λ)cosSθK
is
(λr) dS (8.248)
and
φ
2
=
q
AM
+
∞
0
cosλzdλ
∞
0
M(S
1
λ)cosh S(π −θ)K
is
(λr) dS (8.249)

256 8 Direct Current Field Related Potential Problems
Two boundary conditions are used to get two equations
L(S
1
λ)coshSα =M(S
1
λ)coshS(π − α) (8.250)
1
ρ
L (S
1
λ)sinhSα −
1
ρ
2
M (S
1
λ)sinhS (π − α)
=
1
ρ
1
−
1
ρ
2
q.
4
π
2
sinh S (π −α)K
is
(λr
0
) (8.251)
From these two equations L and M can be determined. After a few steps of
algebraic simplifications we get
L (S, λ)=q
4
π
2
.
K
12
sinh 2S (π − α)
sinh Sπ − K
is
sinh S (π − 2α)
(8.252)
=q.
4
π
2
.A(s)
and
M (S, λ)=q.
4
π
2
.
sinh Sπ +sinhS (π − 2α)
sinh Sπ − K
12
sinh S (π − 2α)
(8.253)
=q.
4
π
2
.B(s)
Therefore the expressions for the potentials are
φ
1
=
Iρ
1
2π
⎡
⎣
1
R
+
4
π
2
∞
0
cos λzdλ
∞
0
A(S)coshSθ
K
is
(λr
0
)K
is
(λr) ds
⎤
⎦
(8.254)
φ
2
=
Iρ
1
2π
⎡
⎣
1
R
+
4
π
2
∞
0
cos λzdλ
∞
0
B(S)coshS(π − θ)
K
is
(λr
0
)K
is
(λr) ds
⎤
⎦
. (8.255)
To get potential on the surface, one has to put θ =0andget.
A (S)=
K
12
sinh 2S (π − α)
sinh Sπ − K
12
sinh S (π − 2α)
(8.256)
where K
12
=(ρ
2
− ρ
1
)/(ρ
2
+ ρ
1
), the reflection factor

8.5 Geoelectrical Potentials for an Anisotropic Medium 257
8.5 Geoelectrical Potentials for an Anisotropic Medium
8.5.1 General Nature of the Basic Equations
In an anisotropic medium
J
x
=
1
ρ
x
E
x
,
J
y
=
E
y
ρ
y
and J
z
=
E
z
ρ
z
(8.257)
where ρx, ρyandρz and Ex,Ey an d Ez are the resistivities and fields along
the principal axes of anisotropy x,y,z. The equation of continuity div
J=0in
a source free region may be written as
∂
∂x
E
x
ρ
x
+
∂
∂y
E
y
ρ
y
+
∂
∂z
E
z
ρ
z
= 0 (8.258)
For a homogeneous but anisotropic medium. This equation reduces to
1
ρ
x
∂
2
φ
∂x
2
+
1
ρ
y
∂
2
φ
∂y
2
+
1
ρ
z
∂
2
φ
∂z
2
= 0 (8.259)
For a homogeneous and isotropic medium, (8.259) reduces to
∂
2
φ
∂x
2
+
∂
2
φ
∂y
2
+
∂
2
φ
∂z
2
=0sinceρ
x
= ρ
y
= ρ
z
(8.260)
For an anisotropic medium let us choose a new sets of coordinates, s uch that
ξ = x
√
ρ
x
,η = y
√
ρ
y
andζ = z
√
ρ
z
and (8.259) reduces to
∂
2
φ
∂ξ
2
+
∂
2
φ
∂η
2
+
∂
2
φ
∂ζ
2
= 0 (8.261)
The solution of the equation is
φ =
C
(ξ
2
+ η
2
+ ζ
2
)
1/2
(8.262)
where C is the constant of integration.
⇒
C
ρ
x
x
2
+ ρ
y
y
2
+ ρ
z
z
2
(8.263)
The expression for the equipotential surface is given by
ρ
x
x
2
+ ρ
y
y
2
+ ρ
z
z
2
=R
2
(8.264)
Equation (8.264) is an equation of an ellipsoid. The axes of the ellipsoid coin-
cide with the principal axes of anisotropy. The current densities are given by

258 8 Direct Current Field Related Potential Problems
J
x
= −
1
ρ
x
∂φ
∂x
=
Cx
ρ
x
x
2
+ ρ
y
y
2
+ ρ
z
z
2
3/2
(8.265)
J
y
= −
1
ρ
y
∂φ
∂y
=
Cy
ρ
x
x
2
+ ρ
y
y
2
+ ρ
z
z
2
3/2
(8.266)
J
z
= −
1
ρ
z
∂φ
∂z
=
Cz
ρ
x
x
2
+ ρ
y
y
2
+ ρ
z
z
2
3/2
(8.267)
Here current lines are straight lines spreading out radially from the source
similar to that happen s in an isotropic medium. The electric lines of force
in an anisotropic medium form a family of curvilinear trajectories orthogonal
to the equipotential surfaces. They do not coincide with the direction of the
current lines except along the principal axes.
In geological sedimentary rocks the anisotropies are along and at right
angles to the plane of stratification. Two resistivities are horizontal resistiv-
ity ρ
l
(parallel to the plane of stratification) and vertical and the transverse
resistivity ρ
t
(perpendicular to the plane of stratification). If the plane of
stratification is closer as the xy plane then (8.259) reduces to
1
ρ
l
∂
2
φ
∂x
2
+
∂
2
φ
∂y
2
+
1
ρ
t
∂
2
φ
∂z
2
=0. (8.268)
The expression for equip otential surface is given by
x
2
+y
2
+(ρ
t
/ρ
l
)z
2
= constant (8.269)
i.e., the e qu ipotential surfaces are ellipsoid of revolution around the z-axis.
For an anisotropic medium, two more parameters are defined. They are
λ =
ρ
t
/ρ
l
and ρ
m
√
ρ
t
ρ
l
(8.270)
where λ is called the coefficient of anisotropy and ρ
m
is the root mean square
resistivity of the media. From (8.269), we get
ρ
m
= λρ
l
=
1
λ
ρ
t
(8.271)
The solution of (8.268) may now be written as
φ =
C
ρ
1/2
l
x
2
+y
2
+ λ
2
z
2
1/2
. (8.272)
The current densities are
