Roy K.K. Potential theory in applied geophysics

Подождите немного. Документ загружается.

7.6 Solution of Laplace Equation in Spherical Polar Co-ordinates 189

Fig. 7.16. Conical equipotential surface for θ dep endence

Similarly one can have the value of Q

(x) for any value of n. The solution of

the Legendre’s equation is



n=0

(x) + B

(x)}. (7.214)

Therefore the general solution of the Laplace equation in spherical co-ordinates

can be written as

φ =





n+1



(cos θ)+D

(cos θ))

CosmΨ+F

Sin mψ) (7.215)

Now

(1) = 1, P

(−1) = (−1)

, P

(0) = 0,

(1) = ∞, Q

(0) = 0, Q

(−1) = ∞. In general P

behavesasabetter

potential function. Therefore in potential theory involving spherical polar co-

ordinates Legendre’s polynomials are used in general as potential functions.

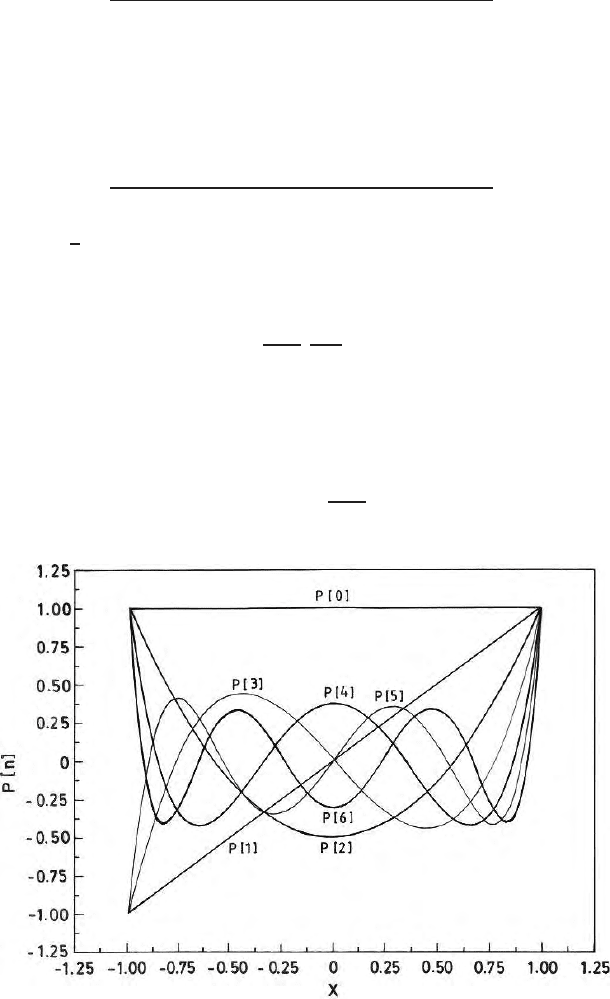
These p olynomials in the Table 7.1 are Legendre’s polynomials from 0 to 6th

degree. Each of these polynomials satisfy Legendre’s diﬀerential equations for

any value of n. The general expression of the Legendre’s polynomial P

(x) is

given by

(x) =



r=0

(−1)

(2n −2r)!

r!(n − r)!(n − 2r)!

n−2r

(7.216)

190 7 Solution of Laplace Equation

Table 7.1.

(x)

(x) = 1

(x) = x

(x) = 1/2(3x

− 1)

(x) = 1/2(5x

− 3x)

(x) = 1/8(35x

− 30x

+3)

(x) = 1/8(63x

− 70x

+ 15x)

(x) = 1/16(231x

− 315x

+ 10x

− 5)

where N =

whennisevenandN=(n− 1)/2 when n is odd. Figure (7.17)

shows that the Legendre’s polynomials are o rthogonal to each other. The

Radriques’ formula for the Legendre’s polynomial is

(x) =

− 1)

(7.217)

where n is the degree of the polynomial.

One can prove that (Ramsay 1940),



−1

(x)P

(x)dx =



0, if n =m

2n+1

if n = m

. (7.218)

Fig. 7.17. Legendre’s polynomial for P(0) to P(6)

7.6 Solution of Laplace Equation in Spherical Polar Co-ordinates 191

The general expression for the Legendre’s function of the second kind is given

(x) =

r=∞



r=0

(n + 1)!(n + 2r)!

r!(2n + 2r + 1)!

−h−2r−1

(7.219)

(x) is an inﬁnite series as mentioned and is generally not used as a potential

function. So the general solution of the Legendre’s equation

Y=AP

(x) + BQ

(x) (7.220)

reduces to

Y=AP

(x).

Problem 1

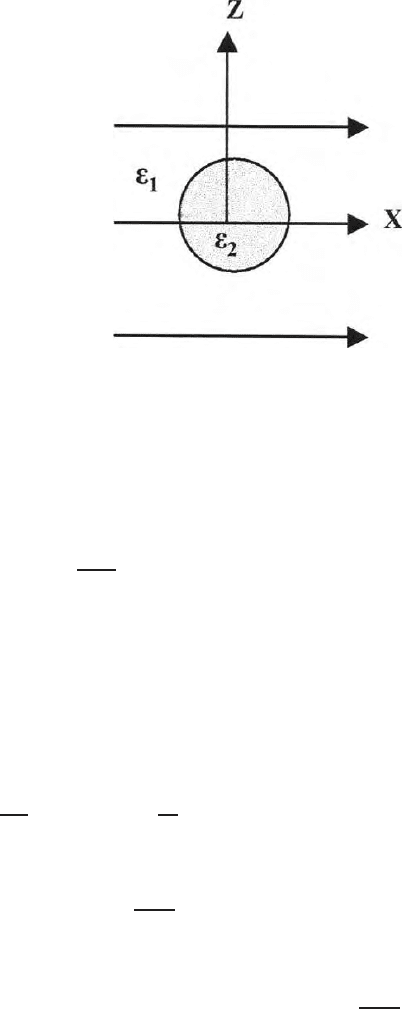
Find out the nature of distortion of the p otential ﬁeld when a sphere of elec-

trical permittivity ∈

is placed in a medium ∈

in the presence of an uniform

ﬁeld (Fig. 7.18).

A spherical body of electrical permittivity ∈

is placed in a medium of

electrical permittivity ∈

in the presence of an uniform ﬁeld E

along the z

direction. Here the perturbation potential will be a function of r and θ.

Hence

φ = −E

Z+Constant.

= −E

rcosθ + Constant. (7.221)

This is the expression for the potential in an uniform ﬁeld. When we

introduce the anomalous body, having diﬀerent physical property, in the ﬁeld,

the perturbation p otential will get added in the vicinity of the b ody. The

perturbation potentials outside and inside the body will be diﬀerent and are

given by

= φ

+ φ

′

and

= φ

+ φ

′′

(7.222)

where φ

is the source p otential, φ

′

and φ

′′

are respectively the perturbation

potentials outside and inside the body.

In the medium 1, i.e., outside the body, the perturbation potential is

′

∞



n=1

n+1

(cos θ). (7.223)

Since the potential ou tside dies down with distance,

n+1

is the solution and

(cos θ) is a better potential function. The potential inside is given by

192 7 Solution of Laplace Equation

Fig. 7.18. Distorsion in current ﬂow ﬁeld in the presence of a spherical body

′′

∞



n=1

(cos θ). (7.224)

Therefore, potentials both outside and inside are given by

∞



n=1

n+1

(cos θ) −E

rcosθ (Potential outside) (7.225)

and



n=1

(cos θ) − E

rcosθ(Potential inside). (7.226)

Applying the two boundary conditions, i.e.,

i) φ

r=a

= φ

r=a

ii) ∈



∂φ

∂r





r=a

= ∈



∂φ

∂r





r=a

where ‘a’ is the radius of the sphere, we get



n+1

(cos θ)=



(cos θ) (7.227)

and

−∈

(cos θ)+∈



. −(n + 1) .

n+2

(cos θ)

= −∈

(cos θ)+∈



−(n+1)

(cos θ). (7.228)

7.6 Solution of Laplace Equation in Spherical Polar Co-ordinates 193

Since the source potential is E

rcosθ and cos θ canbeexpressedasP

(cos θ),

it became possible to bring the source and perturbation potentials in the same

format before the boundary conditions are applied. Here P

is the Legen-

dre’s po lyn omial of the ﬁrst order. Since the source potential is in Legendre’s

polynomial of ﬁrst order, the order will remain the same in the perturbation

potential also. Therefore n = 1. So the equations (7.227) and (7.228) simpliﬁes

down to

a (7.229)

−∈



− A

2 ∈

= −∈



+ ∈

. (7.230)

From these two equations, the values of A

and B

,are

(7.231)

and



∈

−∈

∈

+2 ∈

(7.232)



∈

−∈

∈

+2 ∈

. (7.233)

Substituting the values of A

and B

, in (7.225) and (7.226), we get

= −E

r cos θ + E

∈

−∈

∈

+2 ∈

cos θ(Potential outside) (7.234)

and

= E

r cos θ + E

∈

−∈

∈

+2 ∈

r cos θ(Potential inside). (7.235)

= −E

3 ∈

∈

+2 ∈

.r cos θ.

The ﬁelds inside the body are

= −



∂φ

∂r



= E

3 ∈

∈

+2 ∈

cos θ (7.236)

and

= −



∂φ

r∂ θ



= −E

3 ∈

∈

+2 ∈

sin θ. (7.237)

Therefore, the ﬁeld inside the body can be written as



E =(a

cos θ −a

sin θ)



3 ∈

∈

+2 ∈

= a

3 ∈

∈

+2 ∈



. (7.238)

Hence the ﬁeld inside will be par allel to the ﬁeld outside.

194 7 Solution of Laplace Equation

Corollary

Potential at a point on the surface of the earth due to a buried spherical

inhomogeneity of conductivity σ

is placed in a medium of conductivity σ

the presence of a n uniform ﬁeld in direct current domain.

This is the same problem as given in the previous section. Here the direct

current is ﬂowing from a source at inﬁnite distance to generate the uniform

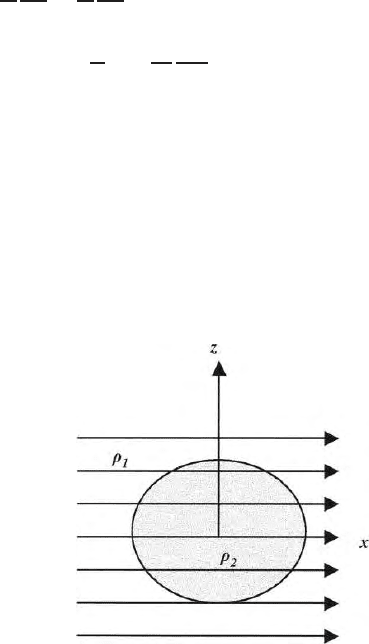
ﬁeld (Fig. 7.19).

The potential will be symmetrical with respect to the polar axis. So the

potential will be independent of the azimulhal angle Ψ.

The solution of the problem is

φ =





−(n+1)



Pn (cos θ). (7.239)

The constants A

and B

can be found out from the boundary conditions.

= φ

and

∂φ

∂r

∂φ

∂r

. at r = a where ‘a’ is the radius of the sphere.

Since



= −

∂φ

∂x

therefore φ

= −



Jρx (7.240)

The potentials outside and inside the body are given by

= −Jρ

∞



n=1

−(n+1)

(cos θ) − Potential outside

= −Jρ

∞



n=1

(cos θ) −Potential inside. (7.241)

Applying the boundary condition we get

Fig. 7.19. Distortion of the equipotential lines due to the presence of a spherical

inhomogenity in an uniform ﬁeld

7.6 Solution of Laplace Equation in Spherical Polar Co-ordinates 195



−(n+1)

(cos θ)=



(cos θ) (7.242)

and

−Jρ



. −(n + 1)a

−(n+2)

, P

= −

Jρ

.ρ



n−1

(cos θ) .

(7.243)

Since the source potential has P

terms, (the Legendre’s polynomial of the

ﬁrst order) the p erturbation potential also will have only P

terms. Only A

and B

will exist and other ter ms, viz A

, A

...A

, B

...B

are all zero.

Therefore

=Jρ

− ρ

+2ρ

and B

=Jρ

− ρ

+2ρ

(7.244)

Hence the potentials outside and inside are given by

= −Jρ

rcosθ +Jρ

− ρ

+2ρ

. cos θ (7.245)

= −Jρ

rcosθ +Jρ

− ρ

+2ρ

.rcosθ (7.246)

= −



3ρ

+2ρ

rcosθ.

Problem 2

Find the potentials at a point on the surface of the earth in the presence of

a buried spherical inhomogeneity of resistivity ρ

in a half space of resistivity

due to point source of current.

A sphere of radius ‘a’ and resistivity ρ

is placed at a depth Z (i.e., the

depth to the centre of the sphere from the surface i.e. air earth boundary)

in a medium o f resistivity ρ

(Fig. 7.20). The distances between the current

electrode at A and potential electrode at P is R, the electrode separation.

The distance from the source to the center of the sphere and from ‘O’ to ‘P’

are respectively ‘d’ and ‘r’. ∠AOP is the angle subtended by A and P at the

center ‘O’. We have to determine the angle θ for each move of the current and

potential electrodes together or separately.

To solve this problem, we shall ﬁrst co nsid er the medium to b e a homog e-

nous and isotropic free space. A spherical body of resistivity ρ

and radius ‘a’

is embedded in a medium of resistivity ρ

. Once the problem is solved in full

pace, the air earth boundary can be bro u ght.

Considering the eﬀect o f image, the potential can be doubled and the

solution ca n be o b t ained within 5 % error.

The perturbation potential function is

φ =





−(n+1)



(cos θ) (7.247)

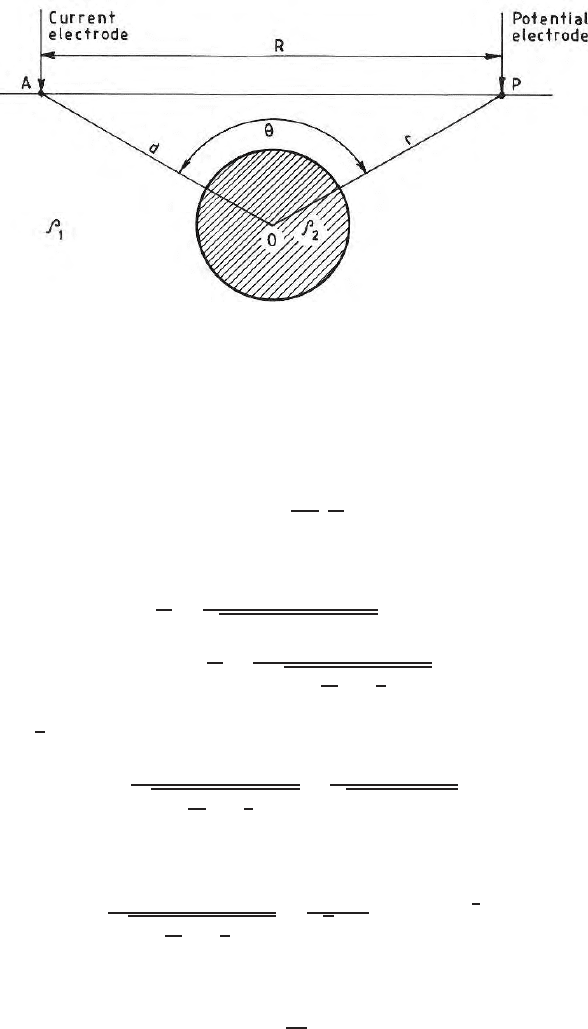
196 7 Solution of Laplace Equation

Fig. 7.20. Two electrode response due to a buried spherical b ody having conduc-

tivity contrast with the host rock; Geometry of the p roblem is shown

in this problem also. Figure (7.20) shows the geometry of the problem and the

location of the current and potential electrodes. In a full space the potential

at P due to a current electrode at A is given by

Iρ

4π

(7.248)

where R = AP. Here R

− 2rd cos θ.So

√

− 2rd cos θ

⇒



− 2

cos θ

(7.249)

Let u =

and x = cos θ,Then



− 2

cos θ

√

1+u

− 2ux

(7.250)

Let ν =2ux− u

So,



− 2

cos θ

√

1 −ν

=(1−ν)

−

After binomial expansion and substituting the values of ν we get

=1+ux+



− 1



+ (7.251)

7.6 Solution of Laplace Equation in Spherical Polar Co-ordinates 197

Since

(x) = 1, P

(x) = x, P

(x) =



− 1



, P

(x) =



− 3x



we can write



− 2

cos θ

(x) u

(x)u

(x) u



(x) u



(x)





. (7.252)

So, the source potential is

4π

∞



n=0

(cos θ)





Therefore the potential inside and outside assuming full space condition is

Iρ

4π

∞



n=0





(cos θ)+

∞



n=1

−(n+1)

(cos θ)

(Potential outside) (7.253)

and

Iρ

4π

∞



n=0





(cos θ)+

∞



n=0

(cos θ).

(Potential inside) (7.254)

Now applying the boundary conditions, at r = a where ‘a’ is the radius of the

sphere.

Iρ

4π







(cos θ)+



−(n+1)

(cos θ)

Iρ

4π







(cos θ)+



(cos θ). (7.255)

From the ﬁrst boundary conditions, i.e., φ

= φ

at r = a

Iρ

4π



n−1

n+1

(cos θ)+



−(n + 1)B

−(n+2)

(cos θ)

Iρ

4π



n−1

n+1

(cos θ)+



n−1

(cos θ). (7.256)

From the second boundary con d it ions, i.e., J

at r = a, we write the

nth term (these boundary conditions hold good for all the terms) as follows

198 7 Solution of Laplace Equation

4π

n−1

n+1

− (n + 1)

−(n+2)



ρI

4π

n−1

n+1

+nA

n−1

⇒

4π

n−1

n+1

−

4π

n−1

n+1

(n + 1) A

n−1

⇒

4π

n−1

n+1



− ρ

n−1



n+ρ

+ ρ

⇒ A

Iρ

2π

(ρ

− ρ

)

n+ρ

n+1

= ρ

Iρ

4π

n+1

(7.257)

where

(ρ

− ρ

(ρ

n+ρ

)

2n+1

Iρ

4π

n+1

2n+1

Therefore

4πR



1ρ

4π

n+1

(cos θ). (7.258)

and

Iρ

4π

Iρ

4π

∞



n=1

2n+1

n+1

(cos θ).

(Potential outside) (7.259)

Now if we bring the air earth boundary, we get

Iρ

2π

)

∞



n=0

2n+1

n+1

(cos θ)

. (7.260)

With this approximation the solution can be obtained within 5% error. Once

the response for two electrode conﬁguration is obtained (Fig. 7 . 21), one can

compute the response for any other electrode conﬁguration since the principle

superposition is valid.

7.6.6 When Potential is a Function of all the Three Coordinates

Viz, Radial Distance, Polar Angle and Azimuthal

Angle,i.e., φ =f(r, θ, ψ)

When potential is a function of all the three coo rdinates, i.e. = f(r, θ, ψ), the

Laplace equation in spherical polar coordinate (7.174) can be solved applying

the method of separation of variables in the form