Roll Forming Handbook / Edited by George T. Halmos

Подождите немного. Документ загружается.

2. The forces acting on the strip in the longitudinal ( x )direction, which is equal to the sum total of

longitudinal stress occurring in it, should be equal to the tension or compression acting on the

strip between stands.

3. The forces acting on the strip in the transversal direction should satisfy the equilibrium condition.

The stress and strain componentsinthe strip,which change as it movesalong D.C.S. are analyzed by

using the elastoplastic deformation theory. The calculative procedure will be explained in the next

section. Forthe analysis and calculation, the strip is divided in the transversal direction into appropriate

numbers of elements as shown in Figure11.30.

11.4.3 GeometryofDeformed Strip and Element, and Deﬁnition of Strain

Increments Occurring in Them

The deformation process of the strip is followed up and analyzed step-by-stepasitmoves from #(i )-rolls

to # ð i þ 1 Þ -rolls. Forthis purpose, the process is divided into appropriate numbers of deformation steps.

In the following discussion, the concerned step being discussed is generally denoted as the ( k )th

deformation step or simply ( k )th step.When the analysis of deformation of the strip has been ﬁnished

from the ﬁrst step to the ð k 2 1 Þ th step,the analysis of ( k )th step is performed as follows.

At ﬁrst, X coordinate of the entr y(front) end of the strip,denoted by X

k þ 1

; is established (Figure11.29

and Figure 11.30). As mentioned already,the sheet strip is preliminarily divided into appropriate

Deformed Curved Surface

of Metal Sheet

∆ I

= ∆ X

:Initial Length

∆ X k :(Length at the k − th Step)

( X

k +1

, Y

k +1, j +1

)

( X

, Y

k , j +1

)

( X

, Y

k , j

)

X = X

#(i +1)− roll

X = X

# i − roll

j +1

k +1

( X

k +1

, Y

k +1, j

)

Sheet Strip

j +1

y =Const.

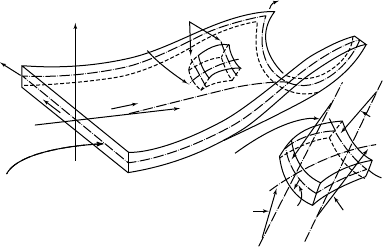
FIGURE 11.29 Geometryofstrip which moves along the deformed curvedsurfacefrom #(i )-rolls to # ð i þ 1 Þ -rolls

under the equilibrium conditions for longitudinal and transversal forces.

Sheet Strip at Initial Stage

Position of Entrance Guide

( k –1)–th Step

( k )–th Step

#1–Roll Profile

∆ l

k,j+1

∆ b

k+1,j

k+1,j +1

∆ l

k − 1,j +1

∆ l

k,j

∆ l

k,j

:Length of Strip at the k-th Step

∆ b

k,j

:Width of Element at the k-th Step

∆ X

−

∆

∆ b

∆

∆ b

k,j

∆ l

k − 1,j

Dividing Point

FIGURE 11.30 Acontinuous strip divided into narrow segments (strips) in the longitudinal direction and each

strip is divided into sheet elements in the transversal direction. Strain increments occurring in each sheet element are

calculated by the presented method and equations.

Roll Forming Handbook11-22

numbers of elements in the transversal direction. The coordinates of ( j )th dividing point (nodal point)

on its front cross-section at the ( k )th step is denoted as ( X

k þ 1

; j ; Y

k þ 1

; j ; Z

k þ 1

; j ). Throughthe analysis

of the ð k 2 1 Þ th step,the coordinates of the same dividing point at that step havebeen obtained and

denoted as ( X

; j ; Y

; j ; Z

; j )are considered to be those of the ( j )th dividing point on the rear cross-

section of the sheet strip.

From these geometrical relations, the longitudinal membrane strain increment ð d 1

Þ ; occurring in

the ( j )th element of the sheet strip at the ( k )th step,iscalculated by Equation 11.3. Following

similar considerations and using the geometrical relation between twotransversally adjacent dividing

points, the transversal membrane strain increment ð d 1

Þ ; occurring in the same element, is also

calculated by Equation 11.4.

ð d 1

¼ðD ‘

2 D ‘

k 2 1

;

Þ = D ‘

k 2 1 ; j

ð 11: 3 Þ

ð d 1

¼ðD b

2 D b

k 2 1 ; j

Þ = D b

k 2 1 ; j

ð 11: 4 Þ

Here,

D ‘

k ; j

¼ð D X

k ; j

þ D Y

k ; j

þ D Z

k ; j

1 = 2

D b

k ; j

¼ D b

k 2 1 ; j

· {1: 0 2

· ð d 1

k ; j

}

D X

k ; j

¼ X

k ; j

2 X

k 2 1 ; j

D Y

k ; j

¼ Y

k ; j

2 Y

k 2 1 ; j

D Z

k ; j

¼ Z

k ; j

2 Z

K 2 1 ; j

¼ 0 : 0 , 1 : 0: membrane strain ratio.

Thus,the membranestrain increments ð d 1

xm;

d 1

Þ in the x -direction (longitudinal direction), and in

y -direction (transversaldirection) occurring in the ( j )th element of the strip at the ( k )thstep aredeﬁned. All

of the geometricalrelationships for these equations areshown in Figure 11.30. The membrane strain ration

is determined so as to satisfythe equilibrium of the transversalforce actingonthe element concerned.

The bending strain increments ð d 1

; d 1

Þ in the x -direction and y -direction occurring in the ( j )th

element of the sheet strip at the ( k )th step are deﬁned as follows by using avariable

.Here,

represents

the distancebetween the respective layer of sheet element and its neutral curved surface.Inthis analysis,

this neutral curvedsurface is considered to be the midlayerofsheet element, and the midlayercoincides

with D.C.S. (Figure 11.31).

ð d 1

k ; j

· {1= ð

k ; j

2 1 = ð

k 2 1 ; j

} ð d 1

k ; j

· {1= ð

k ; j

2 1 = ð

k 2 1 ; j

} ð 11: 5 Þ

x=Const.

( r

)

k –1,j

( r

)

k –1,j

(de

)

k , j

= h • (1/( r

)

k , j

− 1/(r

)

k − 1,j

(de

)

k , j

= h • (1/( r

)

k , j

− 1/(r

)

k − 1,j

( r

)

k , j

( r

)

k , j

y=Const.

Neutral curved surface

:Dis

tanc

rom

neu

tral

surf

ace

FIGURE 11.31 Schematic illustration of bending deformation of sheet element.

Behavior of Metal Strip During Roll Forming 11-23

Here, the curvatures of the element are deﬁned in the x -direction and in the y -direction by the following

equations, respectively.

1 =

¼ L = E ; 1 =

¼ N = G ð 11: 6 Þ

E , G , L ,and N are the “normalized parameters” of the curved surface,which are deﬁned by the general

theoryofmathematics of geometry. If necessary, the curvatures ð

x ;

Þ can be calculated approximately

from the geometrical relationships between coordinates of the dividing points (nodal points) of the

elements.

By summing the incremental membrane strains and the incremental bending strains, the total strain

increments that occur in the ( j )th element of the strip at the ( k )th step are obtained. From the strain

increments, the stress increments occurring in the respective element can be calculated by using the

elastoplastic constitute equations. The details of the equations and the mathematical procedure are

described in the next section.

11.4.4 Procedure to Optimize Deformed Curved Surface (D.C.S.)

By integrating the strain and stress increments from the 1st step to the ( k )th step,the strains and stresses

accumulated in each element of the strip at the ( k )th step are obtained. This means that the distribution

and transition behavior of stress and strain components occurring in the strip can be calculated while it

moves from the ﬁrst step to the ( k )th step.

The longitudinal force F

acting on the strip is calculated by summing the longitudinal stress

component F

distributed on the cross-section of the strip.Ifthe value of F

is not equal to the tension

or compression between stands given by the working condition, then the assumed value of X

k þ 1

considered to be inappropriate. Therefore, with an aim towards getting abetter approximation, the

value of X

k þ 1

is modiﬁed, following the mathematical theoryfor optimization. Then, the above-

mentioned mathematical procedurefor analyzing the deformation of the strip at the ( k )th step is

repeated. This amendment of the value of X

k þ 1

is repeated until the value of F

becomes equal to the

given value.

When the analysis of deformation of the strip,which moves from #(i )-rolls to # ð i þ 1 Þ -rolls, has been

ﬁnished, the total powerofdeformation

W ; which is dissipated in the strip deformation stage between

these tworoll stands, is calculated. The total power of deformation

W can be calculated by

summing the powerofdeformation dissipated in the strip (or element) while it moves from #(i )-rolls to

# ð i þ 1 Þ -rolls.

Accordingtothe theor yof“energymethod,”the total powerofdeformation

W should havethe

minimum value. When this requirement is satisﬁed, the 3-D deformed shape of the strip and the

distributing stress and strain components obtained by the above analysis are recognized as the best

approximation for those of real deformation.

When the total power of deformation

W is found to be other than the minimum, then the value of the

parameter “ n ; ”which is included in the shape function S ð x Þ ; is modiﬁed. Then the whole analysis of the

deformation of the sheet strip,moving from #(i )-rolls to # ð i þ 1 Þ -rollsalong the modiﬁed D.C.S. and

deﬁned by using the modiﬁed value of “ n ; ”isrepeated. Such modiﬁcation of “ n ”and the whole

procedureofanalysis is repeated until

W becomes minimum.

When the minimization of

W is attained, the analysis is ﬁnished. This analysis is performed for every

between-stand deformation wherethe results, with respect to one between-stand deformation, are used

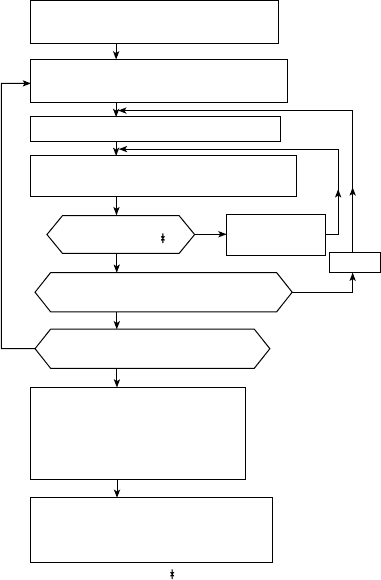
as the initial conditions for the next between-stand deformation. The block diagram of the procedureof

analysis is shown in Figure11.32.

11.4.5 Stress–Strain Relationships (Constitutive Equations)

The stress–strain relationships necessaryfor calculating stress increments are shown by Equa-

tion 11.7 , Equation 11.10, wherethe following assumptions and approximations are employed.

Roll Forming Handbook11-24

(a) The x -and y -directions are considered to coincide with the principal axes of stress and strain in

the strip.

(b) Stress component

in the z (thickness)-direction is very small and can be neglected.

bending strains in each direction.

Thus the following equations are introduced.

d 1

¼ d 1

þ d 1

; d 1

¼ d 1

þ d 1

ð 11: 7 Þ

Forelastic deformation, the stress–strain relationship is expressed by the following equations.

¼ { ð d 1

· d 1

Þ ·E= ð 1 2

Þ }d

¼ { ð

· d 1

þ d 1

Þ ·E= ð 1 2

Þ } ð 11: 8 Þ

Forelastoplastic deformation, the next equation is used.

¼ { ð

þ 2 P Þ · d 1

þð2

þ 2

·PÞ · d 1

} ·E= Q

¼ { ð 2

þ 2

·PÞ · d 1

þð

þ 2 P Þ · d 1

} ·E= Q

ð 11: 9 Þ

Profiles of # i − Roll and #(i +1)− Roll

and Their Positions

Amendment of "n"

by SimplexM

ethod

Stress and Strain Analysis of Sheet

Strip and Element

Longitudinal

Force F

= F

Amendment

of ∆ X

k = k +1

Has the Sheet Strip

reached to #(i +1)− Roll ?

Is the Total Powerof

Deformation Minimum ?

Yes

Results :

etc.

CurvedSurface

Strain Distribution

PowerofDeformation

Analysis of Deformation of Metal

Sheet between #(i +1)− Roll and

#(i +2)− Roll

F :Inter-Stand Te nsion

Deformed CurvedSurface of Metal

Sheet with Assumed Value of "n"

∆ X

is Assumed forthe K − th Step

FIGURE 11.32 Block diagram of the procedure to analyze deformation of asheet strip moving from #(i )-rolls

# ð i þ 1 Þ -rolls.

Behavior of Metal Strip During Roll Forming 11-25

where

P ¼ 2 H·



= 9 ð E 2 H Þ ; Q ¼ R þ 2 ð 1 2

Þ ·P R ¼

þ 2

2 ;



¼ð

1 = 2

¼ð2

Þ = 3 ;

¼ð2

Þ = 3

ð 11: 10Þ

E :Young’sModulus

:Poisson’s ratio

H :Strain hardening rate

11.4.6 Power of Deformation

The total power of deformation

W ,which is dissipated in the strip between #(i )-rolls and # (i þ 1)-rolls,

can be calculated by the next equation.

W ¼

D V

k ; j ; m

· { ð d W

k ; j ; m

þðd W

k ; j ; m

} ð 11: 11Þ

Here, D V

k ; j ; m

is the volume of one layer of strip element, which is obtained by dividing the strip element

in the thickness direction. In order to perform the numerical analysis, the strip or its individual element

is divided into appropriate numbers of layers in the z -(thickness) direction. The index “ m ”represents

the ( m )th layer. D V

k ; j ; m

means the volume of one layer locating at the ( j )th position in the y -direction

and ( m )th position in the z -direction at the ( k )th step of deformation. d W

and d W

denote the power

of plastic deformation and power of elastic deformation for unit volume. By summing the power of

deformation dissipated in each layer,the power of deformation dissipated in one element is obtained. By

summing the power of deformation in each element, the powerofdeformation dissipated in the strip at

the ( k )th step is calculated. Then the total power of deformation

W can be obtained by summing the

powerofdeformation dissipated in the sheet strip at everystep fromthe ﬁrst to the last step of the

deformation between stands.

11.4.7 Some Results of Analysis

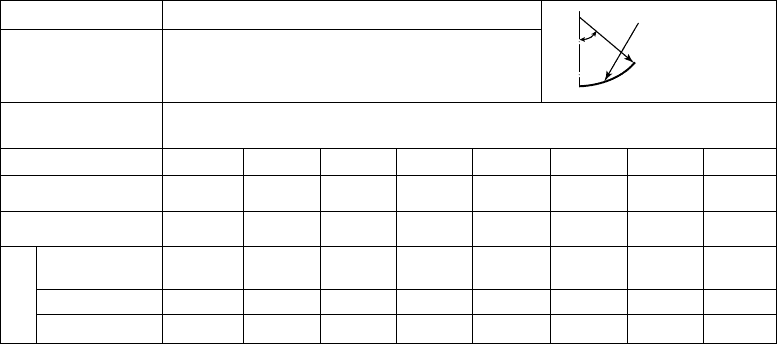
Some results obtained by the above-mentioned method will nowbediscussed with respect to roll

forming processes manufacturing round steel tubes. As an example, for a76.3 mm (3.0 in.) diameter tube

made out of 4.5 mm (0.177 in.) thick mild material, the working conditions such as the required

diameter,mechanical properties of metal, number of rolls, stands, pass-lines, and proﬁles of rollsare

shown in Table 11.1.

TABLE 11.1 General ChartofForming Conditions Employed for Case Study of Analysis

Roll Profile

Dimensions

Mechanical

Properties of

Metal Sheet

Forming

Conditions

Pass-Line

Bottom Line

Const.

Down-Hill

Up-Hill

Stand No.

Profile Angle q

Bending Radius R

Number of

Roll-Stands =8,

Inter-Stand

Distance =800 mm ,Speed =40m/min (mm)

Tube t4.5×φ76.3

E =21000 kgf/mm

n =0.3 , s

=31.5 kgf/mm

H=80kgf/mm

(Sheet t4.5× w280)

#1 #2 #3 #4 #5 #6 #7 #8

30°

229.18

− 10

+ 10

− 20

+ 20

− 30

+ 30

− 40

+ 40

− 40

+ 40

− 40

+ 40

− 40

+ 40

±0 ±0 ±0 ±0 ±0 ±0 ±0 ±0

− 40

+ 40

114.59 76.39 57.30 45.84 42.97 40.44 39.29

60° 90° 120° 150° 160° 170° 175°

Roll Forming Handbook11-26

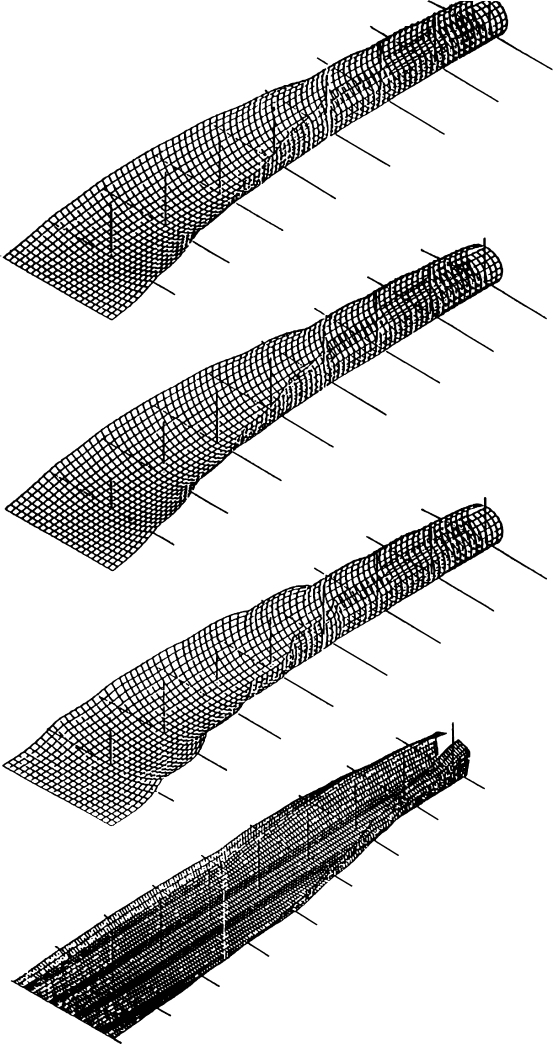
Figure11.33 shows adeformed curvedsurface of the strip being roll formed by eightpairs of rolls

under the given working conditions. The illustrated deformed curvedsurface is the optimized solution of

the analysis for this case. Similar deformed curvedsurfacesfor different working conditions can be easily

obtained. From results like this, it becomes possible to knownot only macroscopic characteristics

4.75

1.63

1.44

1.50

8.25

8.44

13.25

2.44

2.50

2.75

3.06

11.44

11.19

13.75

4.38

6.19

4.38

4.75

5.25

13.25

12.75

14.00

A=0.0

SL =400

SL =600

SL =800

kop

A=0.0

kop

A=3.0

kop

FIGURE 11.33 Some examples of 3-D curved surfaces of strips during roll forming of ERWpipes.

Behavior of Metal Strip During Roll Forming 11-27

of deformation of the strip,but also detailed

featuresoflocal deformation of each portion of

it. Forinstance, the stress and strain distribut-

ing at arbitraryportions can be calculated.

Figure11.34 shows the relationship between

parameter “ n ”included in the shape function

S ð x Þ and the total powerofdeformation

W : The

diagram in the above the ﬁgure shows that the

total power of deformation

W has aminimum

value related to the change of “ n : ”This means

that the above-mentioned mathematical model

and calculation procedure, based on the energy

method, canprovideclear andreasonable

results of simulation.

Figure11.35 shows the calculated relation-

ship between

W and thickness of the strip ð t Þ :

The relationship can be expressed as:

W / t

2 : 18

ð 11: 12Þ

This result coincideswith theempirical

knowledge that the power of deformation is

Parameter n

Bottom Line (B.L.)

Total Po

werofDeformation

/Kgf·m/sec

112

113

114

115

116

117

6810

t 4.5 × f 76.3

Guide~#1− roll

Downhill, n =5.0, W

min

=112.40

B.L.:Horizontal, n =4.4, W

min

=112.93

Uphill, n =3.8, W

min

=113.65

FIGURE 11.34 Relationship between parameter “ n ”included in “ S ð X Þ ”and power of deformation “ W ”being

dissipated in the strip (between the entryguide and # ð 1 Þ -rolls) during roll forming of ERWpipes. The optimum

value of “ n ”gives the minimum value of “ W : ”

100

200

500

Thickness of Metal Sheet t /mm

Total Po

werofDeformation

min

/Kgf·m/sec

35 10 15

t × f 76.3

B.L.:Horizontal

Guide~#1− roll

W=4.24 t

2.18

FIGURE 11.35 Relationship between strip thickness “ t ”

and power of deformation “

W ”dissipated during forming

from entryguide to # ð 1 Þ rolls, during roll forming of ERW

pipes.

Roll Forming Handbook11-28

proportional to ( t

2.0

)invarious sheet forming

processes for which the bending deformation is

dominant co mpared with otheradditive

deformations.

Figure11.36 shows the relationship between

optimum value of “ n ”denoted by “ n

”and sheet

thickness “ t : ”Itclearly shows that “ n

”increases

gradually as “ t ”increases. This means that, when

“ t ”islarge, the strip moving from #(i )-rolls to

# ð i þ 1 Þ -rolls, deform abruptly just in front of

the # ð i þ 1 Þ -rolls. This tendency can be observed

in actual production lines.

Figure11.37 shows some examples of the

dynamic featuresofstrains. This ﬁgure shows the

transition of the longitudinal membrane strain

; occurring at the center,edge and intermediate position of the strip.The transition of 1

is consistently calculated through the whole forming process fromthe ﬁrst roll stand to the eight roll

stand.

The results indicate that large tensile strain occurs, and shows apeak value repeatedly at the edge

portion of the strip during strip deformation between everyforming stands. However,atthe roll gaps, the

transversal distribution of 1

becomes nearly uniform and the value of 1

becomes very small. If it

becomes excessive, this edge elongation causes edge buckling (waviness) and other product defects.

Therefore, in order to design the rollsand pass-schedules for manufacturing good products, it is

important to know the overall behavior and characteristics of 1

as shown in this ﬁgure.

Thus, using the developed simulation method, it becomes possible to predict the distribution and

transition features of each strain component in the strip.Possible problems may be predicted

preliminarily,without actual trials. Therefore, it can be beneﬁcial to predict potential problems without

using actual rolls and to modify the rollsbefore they are made.

11.5 Computerized Design System for Roll Proﬁles

Utilizing mathematical theoryand simulation techniques, computerized rolldesign systems are now

being developed. Such design systems are expected to be useful to develop optimal ﬂower diagrams, roll

proﬁles and roll positions.

f 76.3

Guide~#1− roll

B.L.:Horizontal

5.0

4.6

4.2

3.8

Thickness of Metal Sheet t /mm

Optimized

Parameter

246810 12

FIGURE 11.36 Relationship between sheet thickness “ t ”

and optimized value of “ n ”for roll forming of ERWpipes.

800

− 1

× 10

− 3

Longitudinal Membrane Strain

#1 #2 #3 #4 #5 #6 #7 #8

800 800 800 800 800 800 800

Pass− Line:Bottom Line:Horizontal

t 4.5 × f 76.3

Edge (y=120)

Midst (y=60)

Center (y=0)

FIGURE 11.37 Some calculated results on behavior of longitudinal membrane strain “ 1

”during roll forming of

ERWpipes.

Behavior of Metal Strip During Roll Forming 11-29

Figure11.38 showsthe ﬂowchartofone of these advanced computerized design systems. This system

is able to design aseries of rolls to satisfy manyrequirements, including keeping the magnitude of edge

stretch (edge elongation) belowacritical value. It can also provide aseries of rollproﬁles for aminimum

number of passes without inducing anyproblems. Computerized design systems like this are nowbeing

used for various roll design projects for tubes and light gage section.

The results of application are show in the following sections, where twodifferent criteria for the

optimization of rollproﬁles were introduced.

1. The ﬁrst criterion is for the minimization of edge stretch. The minimization of edge stretch is

attained by making the maximum values of membrane strain ð 1

# i

MAX

,that occurs at the edge

portion during everyinterstand forming process, equal to each other.

2. Thesecondone is forthe equalization of drivingtorquenecessaryfor rolls, wherethe powers of

deformation(

W )

dissipatedinmetal sheetateachinterstanddeformation state aremadeequal to

each other.

11.5.1 Flower Diagrams for Minimizing Edge Stretch

Twoseries of roll proﬁles designed for manufacturing round tubes withsmall t:D ( t ¼ 2 : 3 £

101: 6mm

or 0.090 in. thick £ 4.0 in. diameter) and large t : D ( t ¼ 4 : 5mm £

48.6 mm or 0.177 in. thick £ 1.91

in. diameter) are shown in Figure11.39.These rolls minimize edge stretch. The optimized allocation of

the increment of proﬁle angle D

to each rolland the optimized roll ﬂowers for two cases are shown in

the ﬁgure. It should be noticed that two kinds of roll ﬂowers are shown with the same normalized

dimension. The difference between twosets of roll ﬂowers for small t : D and large t : D is clearly

observed. The predicted values of ð 1

# i

MAX

; ¼ð1

# i

MAX

,(i ¼ 1 ; 2 ; … )are also shown in Figure11.39 and

it can be known that the equalization of ð 1

# i

MAX

; ð i ¼ 1 ; 2 ; … Þ is almost completely attained for each case.

Initial Data

Pass-Line

Roll-Profiles

Mathematical

Simulation

Edge Elongation

Forming Torque

Stress and Strain Distribution

etc.

Optimized Forming Process

Optimization is accomplished

Optimum Design

of Forming Mill

Optimum Design

of Pass-Line

Optimum Design

of Roll-Profiles

initial Roll-Profiles

Critical Values

VII Comparison

•

Mechanical Properties of Sheet

•

GeometryofProduct

Parameters of Forming Mill

•

Number of Roll-Stands

•

Interstand Distance

•

Others (Forming Speed etc.)

FIGURE 11.38 Conceptual illustration of computer-aided engineering and design system for roll forming.(For

design of rolls, roll positions, forming schedules, equipment, and processes.)

Roll Forming Handbook11-30

Figure11.40(a)–(c) shows the optimized increment of proﬁle angle D

# i

allocated to each roll and the

optimized roll ﬂowers for the cases when various pass lines are employed. The dimensions of the round

tube are t ¼ 4 : 5 £

101: 6mm(0.177 in. thick £ 4.0 in. dia). The descent of pass line height, denoted by

DH, is changed in the range from 0.0 to 0.5 XH, where H denotes the depth of the semiformed cross-

section of the strip at each roll stand. In each case, #5 rolls and #6 rolls are ﬁxed on the horizontal line,

wherethe bottom points of the semiformed cross-section at #5 stand and #6 stand are on ahorizontal

line. From these ﬁgures, it can be seen that thereare suitable roll ﬂowers for different pass lines in order to

minimize the edge stretch.

11.5.2 Roll Flowers for Equalized Power of Deformation

Figure11.41 shows the optimized allocation of the increment of proﬁle angle D

# i

and the optimized roll

ﬂowers for two cases when the values of t : D are small ( t ¼ 2 : 3 £

101: 6mmor0.090 in. thick £ 4.0 in.

diameter) and large ( t ¼ 4 : 5 £

48: 6mmor0.177 in. thick £ 1.91 in. diameter). The ﬁgure also shows

the powerofdeformation

# i

ð i ¼ 1 ; 2 ; … Þ has been attained almost completely.The optimized roll

ﬂower for small t : D shown by bold lines and that for large t : D shown by broken lines are clearly

different from each other.

The effects of diameter D and wall thickness t of tubes on the powerofdeformation

W are summarized

as follows. When the wall thickness t is ﬁxed,

W decreases as the diameter D increases. This is due to the

B.L.:Horizontal

( e

)

MAX

:Maximum Value of Longitudinal

Edge Elongation

( ∆ q ):Increment of Profile Angle

×10

− 3

×10

− 3

t 2.3× f 101.6

t 4.5× f 48.6

#1 23456

#1 23456 #1 23456

#1 23456

Roll No. Roll No.

t 2.3 × f 101.6 t 4.5 × f 48.6

( e

)

MAX

( e

)

MAX

∆ q (deg)

FIGURE 11.39 Some examples of designed roll proﬁles (so-called “roll ﬂowers”) for manufacturing ERWpipes.

They are optimized so that the longitudinal membrane strain “ 1

”isreduced to be minimal.

Behavior of Metal Strip During Roll Forming 11-31