Roff D.A. Modeling Evolution: An Introduction to Numerical Methods

Подождите немного. Документ загружается.

¼ 1 

i¼1

Pbenefit

ð6:21Þ

4. We shall assume a constant mortality per unit time, Pmortality ¼ 0.01. At the

end of the season no further eggs can be laid, meaning that the female is, from

the point of view of natural selection, dead. For computational simplicity we

shall use Psurvival ¼ 1  Pmortality. Thus

Psurvival ¼

0:99 for t<T 1

0:00 for t ¼ T  1



ð6:22Þ

5. Overall ﬁtness is the sum of the ﬁtness increments obtained from each host.

6.6.3 Outcome chart and expected lifetime ﬁtness function

The important feature of this model that differentiates it from previous models is

that the value of the state variable increases as we move toward t ¼ 1, rather than

decreasing. Because no eggs are laid beyond time T, the terminal ﬁtness is F(x, T) ¼

0. Because eggs are laid prior to the calculation of survival, even if the female does

not survive, the state variable takes a positive value. Thus at each time step there

are two possible outcomes, a host is found or a host is not found:

From the above, we have that ﬁtness at time t 1 is made up of two functions, f and g:

Fðx; t  1Þ¼f ðNo host encounteredÞþgðHost encounteredÞð6:23Þ

The function for “No host encountered” is

f ðNo host encounteredÞ¼0:99P

Fðx; tÞð6:24Þ

The function for “Host encountered” is more complicated. The ﬁtness increment

for each combination of host type i and clutch size, c, where c varies from 0 to x,is

i;c

¼ Benefit

i;c

þ 0:99  Fðx  c; tÞð6:25Þ

that is, the beneﬁt from the present clutch plus the ﬁtness expected from the

remaining eggs (x  c). Note that this particular formulation requires estimating

F(0, t), which means that we have to use an index transformation in the coding, as

done in the last scenario. From the series generated by equation (6.25) we obvious-

ly choose the maximum value: thus for the ith host and x ¼ 4, we pick

Host found Survives X

Yes Yes x‐Beneﬁt

i,n

.................................................................................................

Yes No x‐Bene ﬁt

i,n

.................................................................................................

No Yes X

.................................................................................................

No No X

378 MODELING EVOLUTION

i;max

¼ maxfF

i;0

; F

i;1

; F

i;2

; F

i;3

; F

i;4

gð6:26Þ

The expected maximum ﬁtness increment over all host types is then given by

gðHost encounteredÞ¼

i¼1

Pbenefit

i;max

ð6:27Þ

and F(x, t  1) is thus

Fðx; t  1Þ¼0:99P

Fðx; tÞþ

i¼1

Pbenefit

i;max

ð6:28Þ

Mangel and Clark (1988) make the following predictions for this scenario:

Prediction 1: For a ﬁxed number of remaining eggs, older insects should lay larger

clutches than younger insects. The rationale for this prediction is that older

insects are closer to the end of the duration and hence their expected future

ﬁtness is reduced relative to younger females, thereby making present allocation

a higher contribution to overall ﬁtness.

Prediction 2: It also follows from the preceding rationale that older insects are

more likely to choose inferior hosts.

Prediction 3: Because of differing host encounters there will be a distribution of

clutch sizes at any given time.

Prediction 4: As the per period survival decreases, larger clutches will be

observed. This follows from the fact that survival discounts future reproduction

(i.e., Psurvival  Fðx  c; tÞ).

Prediction 2 is not directly addressed by this model, because females only locate

one type of host at a time. Prediction 3 is not directly addressed by the decision

matrix but can be addressed using the decision matrix and simulating the behav-

ior of individual females, as described below.

6.6.4 Calculating the decision matrix

It is more convenient to place the calculations of ﬁtness directly into the function

OVER.PATCHES, which iterates over host types. Rather than storing all cases in

which there are multiple choices of the greatest ﬁtness, the program simply prints

out when these occur: in this example no such cases occur (such cases are more

likely to occur when survival is the ﬁtness criterion). Except for these two changes,

the basic program is the same as the patch-foraging model. (Because the state

variable, number of eggs, is an integer and varies in unit steps, no interpolation is

required.) While one could calculate the single host ﬁtness functions using the

cubic functions within OVER.PATCHES it is more efﬁcient to calculate a Beneﬁts

matrix as given in Figure 6.3 and pass this matrix. The decision matrix gives the

DYNAMIC PROGRAMMING 379

optimal clutch size but what is likely to be of greater interest is the decision matrix

for each host type, as it is this that is required to address Predictions 1 and 4. The

decision matrix for a single host type can be obtained very easily by storing this

value in place of the overall clutch size, that is, to get the decision matrix for host

type 3 use (in OVER.PATCHES)

Temp <- c(F.vectors[Index,1], Best.Clutch[3])

To output the decision matrix for all host types simultaneously requires more

complicated bookkeeping that I leave to the reader. (Given how quickly the

program runs one can simply run the model four times, changing the index

value of Best.Clutch[3] or use the approach given in Scenario 5.) To illustrate

the validity of Predictions 1 and 2, I stored the output for the x ¼ 40 column of the

decision matrix for host type 3 and ran the model with three values of Psurvival:

0.99, 0.90, and 0.80. I then plotted the results using SigmaPlot.

R CODE:

rm(list¼ls()) # Remove all objects from memory

# Set up path for output of text files

setwd(“C:/Documents and Settings/Derek Roff/My Documents/ Mod-

elling Evolution/DYNAMIC PROGRAMMING”) # This will have to be

changed for specific paths

# Function to iterate over patches i.e. over Hosts

OVER.PATCHES <- function(X, F.vectors, Xcritical, Xmax, Xinc,

Npatch, Benefit, Pbenefit, Psurvival)

{

# Create matrix for storing best clutch size for each host type

Best.Clutch <- matrix(0,Npatch)

Index <-1þ (X-Xcritical)/Xinc # Index for X is Xþ1

# Vector of clutch sizes to Index-1

Clutch <- seq(from ¼1, to ¼ Index-1)

# Start fitness accumulation with component for case of not finding

a host

W <- Psurvival*(1-sum(Pbenefit))*F.vectors[Index,2]

for (i in 1: Npatch) # Cycle over patches ¼ Hosts

{

# Calculate “partial” fitness, W.partial for each clutch size

W.partial <- Benefit[2:Index,i] þ Psurvival*F.vectors[Index-

Clutch,2]

# Find largest W.partial and hence best clutch size

Best <- order(W.partial, na.last¼TRUE, decreasing¼TRUE)

Best.Clutch[i] <- Best[1] # Store value of best clutch for

host i

380 MODELING EVOLUTION

# Increment fitness

W <-Wþ Pbenefit[i]*W.partial[Best[1]]

# Test for several equal optimal choices

# Only examine W.partial that contain more than one entry

if(length(W.partial)>1 & W.partial[Best[1]]¼¼W.partial[Best[2]])

{print(“Several possible equal choices”)}

} # End of i loop

F.vectors[Index,1] <- W # Update F(x,t)

# Concatenate F(x,t,T) and the optimal clutch values for host type 2

Temp <- c(F.vectors[Index,1], Best.Clutch[2])

# Add Temp to bottom of F.vectors and rename to Temp

Temp <- rbind(F.vectors, Temp)

return (Temp)

} # End of function

# ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ....

# Function to iterate over states of X

OVER.STATES <- function(F.vectors, Xcritical, Xmax, Xinc,

Npatch, Benefit, Pbenefit, Psurvival, Max.Index)

{

Store <- matrix(0,Max.Index,2) # Create matrix for output

for ( Index in 2 : Max.Index) # Iterate over states of X

{

# For given X call Over.Patches to determine F(x,t,T) and best patch

X <- (Index-1)*Xinc þ Xcritical

Temp <- OVER.PATCHES(X, F.vectors, Xcritical, Xmax, Xinc,

Npatch, Benefit, Pbenefit, Psurvival)

# Extract components. Last row is F(x,t) and best clutch size for

host 2

n <- nrow(Temp)-1

F.vectors <- Temp[1:n,]

Store[Index,] <- Temp[nþ1,] # Save F(x,t,T) and best clutch

size

} # End of X loop

# Add Store values to end of F.vectors for pass back to main program

Temp <- cbind(F.vectors, Store) # Combined by columns

return(Temp) # Return F.vectors and

Store

} # End of function

DYNAMIC PROGRAMMING 381

# ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ....

# MAIN PROGRAM

# Initialize parameters

Xmax <- 40 # Maximum value of X ¼ eggs

Xcritical <- 0 # Lowest value of X ¼ 0 eggs

Xinc <- 1 # Increment in state variable

Max.Index <-1þ (Xmax-Xcritical)/Xinc # Max Index value

Psurvival <- 0.99 # Survival probty per time increment

Npatch <- 4 # Number of patches ¼ hosts

# Create host coefficient matrix from which to get Benefits

Host.coeff <- matrix(0,4,4)

Host.coeff[1,] <- c(-0.2302, 2.7021, -0.2044, 0.0039)

Host.coeff[2,] <- c(-0.1444, 2.2997, -0.1170, 0.0013)

Host.coeff[3,] <- c(-0.1048, 2.2097, -0.0878, 0.0004222)

Host.coeff[4,] <- c(-0.0524, 2.0394, -0.0339, -0.0003111)

# Calculate benefit as a function of

# clutch size (rows) and Host type (columns)

Clutch <- seq(from ¼ 0, to ¼ Xmax)

Benefit <- matrix(0, Xmaxþ1, 4) # Zero to Xmax

for (I.Host in 1:4) # Iterate over host types

{

Benefit[,I.Host] <- Host.coeff[I.Host,1] þ Host.coeff[I.

Host,2]*Clutch þ Host.coeff[I.Host,3]*Clutch^2 þ Host.coeff[I.

Host,4]*Clutch^3

}

Benefit[1,] <- 0 # Reset first row to zero

SHM <- c(9,12,14,23) # Set single host maximum. See text for deri-

vation

# Make all values > than SHM¼0. Note that we use 2 because of zero

class

for (i in 1:4){Benefit[(SHM[i]þ2):Max.Index,i] <-0}

# Probability of encountering host type

Pbenefit <- c(0.05, 0.05, 0.1, 0.8)

Horizon <-

21 # Number of time steps

# Set up matrix for fitnesses

# Column 1 is F(x, t). Column 2 is F(x, tþ1) Both are zero

F.vectors <- matrix(0, Max.Index,2)

# Create matrices for output

FxtT <- matrix(0,Horizon,Max.Index) # F(x,t,T)

# Best clutch size for host 2

Best.Patch <- matrix(0,Horizon,Max.Index)

382 MODELING EVOLUTION

# Start iterations

Time <- Horizon # Initialize Time

while ( Time > 1)

{

Time <- Time -1 # Decrement Time by 1 unit

# Call OVER.STATES to get best values for this time step

Temp <- OVER.STATES(F.vectors, Xcritical, Xmax,

Xinc, Npatch, Benefit, Pbenefit, Psurvival, Max.Index)

# Extract F.vectors

TempF <- Temp[,1:2]

# Update F1

for ( J in 2: Max.Index) {F.vectors[J,2] <- TempF[J,1]}

# Store results

Best.Patch[Time,]<- Temp[,4]

FxtT[Time,] <- Temp[,3]

} # End of Time loop

# Output information. For display add states to last row of matrices

Index <- seq(from¼1, to¼Max.Index)

Best.Patch[Horizon,] <- (Index-1)*XincþXcritical

FxtT[Horizon,] <-(Index-1)*XincþXcritical

Best.Patch[,1:Max.Index] # Print Decision matrix

signif(FxtT[,1:Max.Index],3) # Print Fxt of Decision matrix:

3 sig places

# Plot data as 3d plot and colored grid

y <- Best.Patch[Horizon,2:Max.Index]

x <- seq(from¼1, to¼Horizon-1)

par(mfrow¼c(2,2))

persp(x, y, Best.Patch[1:20,2:Max.Index], xlab¼‘Time’,

ylab¼‘x’, zlab¼‘Optimal clutch size’, theta¼20, ph¼25, lwd¼1) #

3D plot

image(x, y, Best.Patch[1:20,2:Max.Index], col¼terrain.colors

(50), xlab¼‘Time’, ylab¼‘x’, las¼1) # Colored grid

# Output text file for future plotting to test predictions

DATA <- cbind(x, Best.Patch[1:Horizon-1,41])

DATA <- t(DATA)

write(DATA,file¼

“OVIPOSITION.txt”,nc¼2)

OUTPUT:

(Figure 6.5)

DYNAMIC PROGRAMMING 383

Time

Optimal clutch size

510

15 20

Figure 6.5 Results for Scenario 4: Top shows two graphical representation of the

decision matrix and bottom a reduced decision matrix for host type 3.

State variable, x

Time 1234510152025303540

1 112222223333

...................................................................................................................................................

2 112222223333

...................................................................................................................................................

3 112222223333

...................................................................................................................................................

4 112222223333

...................................................................................................................................................

5 112222223333

...................................................................................................................................................

6 112222223333

...................................................................................................................................................

7 112222223333

...................................................................................................................................................

8 112222223333

...................................................................................................................................................

9 112222223333

...................................................................................................................................................

10 112222223333

...................................................................................................................................................

11 112222223333

...................................................................................................................................................

12 112222223334

...................................................................................................................................................

13 112222233344

...................................................................................................................................................

14 112222233344

...................................................................................................................................................

15 112222233445

...................................................................................................................................................

16 112222334456

...................................................................................................................................................

17 112222345667

...................................................................................................................................................

18 1122234567910

...................................................................................................................................................

19 1 1 2 2 2 4 6 8 10 11 13 14

...................................................................................................................................................

20 1234510141414141414

384 MODELING EVOLUTION

The decision matrix is printed out but not shown here. Figure 6.5 shows a reduced

version of this matrix for host type 3 along with two visualizations of the complete

matrix. The most striking point is that, as predicted (Prediction 1), the optimal

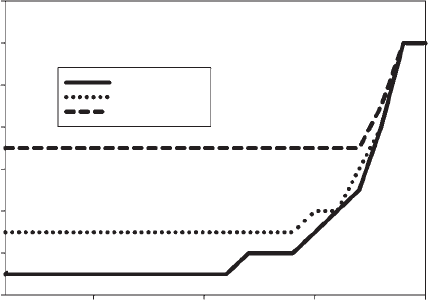
clutch size increases with age. Figure 6.6 shows the effect of varying Psurvival:as

predicted (Prediction 3), the optimum clutch size increases as survival per unit

time decreases.

MATLAB CODE: See Section 6.9.6.

6.6.5 Using the decision matrix: individual prediction

Although the dis tribution of clutch sizes over time can be calculated using the

transition density matrix the construction is very tedious in comparison to using

the individual prediction approach. By running a large number of individuals

(e.g., 1,000–10,000) the resulting distribution will closely approximate the

expected distribution. To obtain the decision matrix for all four hosts the pre-

ceding program was run four times and the decision matrices dumped as text

ﬁles labeled

DM1.txt, DM2.txt, DM3.txt and DM4.txt, the appropriate coding being

DATA <- Best.Patch[1:Horizon-1,2:41]

DATA <- t(DATA)

write(DATA, file¼“DM4.txt”,nc¼40)

The four ﬁles were read back and placed into an array called DM in which the

dimensions represent x, time, and host type. At each iteration over individual and

time a host type has to be allocated based on its probability of occurrence (Pbeneﬁt).

To do this we proceed as follows:

Psurvival = 0.99

Psurvival = 0.95

Psurvival = 0.80

Time

Optimal Clutch Size

10 15 20

Figure 6.6 Effect of varying Psurvival on the optimal clutch size for host type 3 given x =

40. Plot generated using SigmaPlot.

DYNAMIC PROGRAMMING 385

Step 1: Multiply all probabilities by a common factor so that they are integers. In

the present case the set of probabilities are 0.05, 0.05, 0.1, and 0.8, and hence the

appropriate multiplier is 100, giving 5, 5, 10, and 80, respectively. Create a vector

with these numbers:

Times <- c(5,5,10,80).

Step 2: Create a vector, Host.Type, in which there are 5 “1”s, 5 “2”s, 10 “3”s, and 80

“4”s:

Host.Type <- c(rep(1,Times[1]), rep(2,Times[2]), rep(3,Times

[3]), rep(4,Times[4]))

Step 3: For each individual create a vector of length Horizon (the total number of

time increments) of random integers between 1 and 100:

Host <- ceiling(100*runif(Horizon))

Step 4: The host type chosen at time interval i is Host.Type[Host[i]]. The

probability of occurrence is equal to the probabilities given by Pbenefit. Survival

is computed by generating a vector of (length ¼ Horizon) random numbers

between 0 and 1: values greater than 0.99 indicate that the female dies in that

time period and are set to zero, all other values then being set to 1:

Survival <- runif(Horizon) # Vector of survival probabilities

Survival[Survival>Psurvival] <-0

Survival[Survival!¼0] <- 1 # Set all other values to 1

The initial distribution of egg complement (x) is set as a normal distribution with

mean 20 and standard deviation of 5, and converted to integer values:

x.init <- ceiling(rnorm(N.Ind, mean¼20, sd¼5))

Because clutch sizes are integral, the results are plotted using the bar graph

routine rather than the histogram routine.

R CODE:

rm(list¼ls()) # Remove all objects from memory

setwd(“C:/Documents and Settings/Derek Roff/My Documents/Mod-

elling Evolution/DYNAMIC PROGRAMMING”)

Xmax <- 40 # Maximum value of X ¼ eggs

DM1 <- read.table(file¼“DM1.txt”) # Cols ¼ x rows¼time

DM2 <- read.table(file¼“DM2.txt”)

DM3 <- read.table(file¼“DM3.txt”)

DM4 <- read.table(file¼“DM4.txt”)

# Create an array for Decision matrix

DM <-

array(0,c(20,Xmax,4))

# time, state, host

for (i in 1:20)

{

for ( j in 1:Xmax)

386 MODELING EVOLUTION

{

DM[i,j,1] <- DM1[i,j]; DM[i,j,2] <- DM2[i,j]

DM[i,j,3] <- DM3[i,j];DM[i,j,4] <- DM4[i,j]

}}

# Probability of encountering host type

Pbenefit <- c(0.05, 0.05, 0.1, 0.8)

Times <- c(5,5,10,80)

# Create Vector for Host type probability

Host.Type <- c(rep(1,Times[1]),rep(2,Times[2]),rep(3,

Times[3]), rep(4,Times[4]))

Psurvival <- 0.99 # Survival probability per time increment

Horizon <- 10 # Number of time steps

set.seed(10) # Initialise random number generator

N.Ind <- 1000 # Number of individuals

Output <- matrix(0,N.Ind,Horizon) # Allocate space for output

# Generate initial values of x from normal distribution

x.init <- ceiling(rnorm(N.Ind, mean¼20, sd¼5))

for (Ind in 1:N.Ind) # Iterate over individuals

{

# Generate vectors for choosing the Host type and probability of

survival

Host <- ceiling(100*runif(Horizon)) # Vector of host types

Survival <- runif(Horizon) # Vector of survival probabilities

# Set all values of Survival > Psurvival ¼ 0

Survival[Survival>Psurvival] <-0

Survival[Survival!¼0] <- 1 # Set all other values to 1

x <- x.init[Ind] # Initial value of x

for (Time in 1:Horizon) # Iterate over time periods

{

if( x>0) # If eggs remaining calculate clutch size using DM

{

Clutch.Size <- DM[Time,x,Host.Type[Host[Time]]]

Output[Ind,Time] <- Clutch.Size # Store clutch size

# Compute new value of x

x <- x-Clutch.Size

}

x <- x*Survival[Time] # Set x¼0 if female does not survive

} # end of Time loop

} # End of Ind loop

par(mfcol¼c(5,2)) # Set graphics page to 5 rows and 2 columns

# Iterate over time and plot bar graphs of clutch size

for (i in 1:10 )

{

Data <-

Output[,i]; Data <- Data[Data>0] # Eliminate zeroes

xbar <- mean(Data) # Mean clutch size

DYNAMIC PROGRAMMING 387