Roff D.A. Modeling Evolution: An Introduction to Numerical Methods
Подождите немного. Документ загружается.

Step 5: The next patch type is selected and Steps 3 and 4 repeated.
Step 6: After the fitnesses of all patch types have been calculatedthe patch giving
the highest fitness is selected. The optimal patch value is the value of i that gives
the maximum value of Wðx; i; t 1Þ:
Fðx; t 1Þ¼maxfWðx; 1; t 1Þ; Wðx; 2; t 1Þ; Wðx; 3; t 1Þg ð6:7Þ
If there were k patches then the choice would be among the k survivals. The R
code is
# Now find optimal patch. Best row is in Best[1]
Best <- order(RHS, na.last¼TRUE, decreasing¼TRUE)
Best.Patch <- Best[1]
The “best” survival is stored in the cell of the first column of the appropriate row
of F.vectors, that is F.vectors[X,1] < RHS[Best[1]].
Step 7: We now pass back the modified matrix F.vectors, the modified value of
F.vectors[X,1], and the best patch number, Best.Patch, back to OVER.
STATES. This is done by concatenating F.vectors[X,1] and Best.Patch to-
gether
to form a 1 2 matrix called Temp and then concatenating F.vectors
and Temp together:
# Concatenate F(x,t,T) and the optimal patch number
Temp <- c(F.vectors[X,1], Best.Patch)
# Add Temp to bottom of F.vectors and rename to Temp
Temp <- rbind(F.vectors, Temp)
return (Temp)
Step 8: Temp is passed back to OVER.STATES (where it is also called Temp, but this
is arbitrary), where F.vectors is updated and the optimal patch number and
survival are stored in a two-column matrix called Store. Note that the updating of
F.vectors does not affect further calls to OVER.PATCHES, because only the
second column of F.vectors is used. The first column is being used to store
the values to be used in the next iteration of Time.
Step 9: Another state is selected, which now would be Xmin þ 1 and Steps 2–8 are
repeated.
Step 10: After all state values have been examined F.vectors and Store are
concatenated into a four-column matrix called Temp, the first two columns
containing F.vectors, the third column F(x, t), the survival, and the fourth
column the best patch number. Temp is passed back to the main program.
Step 11: To store the values of F(x, t), and the best patch number two matrices,
named FxtT and Best.patch, respectively, were created at the start of the main
program. Each matrix consists of Horizon number of rows (20 here) and Xmax
columns. Thus, rows correspond to time and columns to states. The first Xcritical
columns are redundant as they are never used. However, setting up the matrices
in this manner is convenient because columns then correspond to state values.
The values from OVER.STATES are passed back into a matrix called Temp, which
348 MODELING EVOLUTION
is then disassembled into the components corresponding to F.vectors (called
TempF), survival, and the best patch. The values in the second column of F.vectors
are updated using the values in the first column of TempF. This updating
means that in the new round the survival probability calculated in FITNESS is
the survival from time t to time T (¼Horizon) given the optimal choice of patches.
The lines of coding are
# Extract F.vectors
TempF <- Temp[,1:2]
# Update F1
for ( J in Xmin: Xmax) { F.vectors[J,2] <- TempF[J,1]}
# Store results
Best.Patch[Time,] <- Temp[,4]
FxtT[Time,] <- Temp[,3]
Step 12: Delete one unit from Time and repeat all previous steps. Once Time is
less than one we exit the while loop and print out the two matrices, as shown in
Table 3.1.
The complete coding in R and MATLAB is given below (note that the coding
here, and throughout this chapter, is very similar and differs primarily as a
consequence of syntax or the name of the built-in functions).
R CODE:
rm(list¼ls()) # Remove all objects from memory
# Function to calculate fitness when organism is in state X
FITNESS <- function(X, Xcritical, Xmax, Xmin, Cost, Benefit,
Pbenefit, Pmortality, F.vectors)
{
# State in patch if forager finds food
X.Food <- X - Cost þ Benefit
# If X.Food greater than Xmax then X.Food must be set to Xmax
X.Food <- min(X.Food, Xmax)
# If X.Food less than or equal to Xcritical then set to Xcritical
X.Food <- max( X.Food, Xcritical)
# State in patch if forager does not find food
X.NoFood <- X - Cost
# If X.NoFood is less than Xcritical set X.NoFood to Xcritical
X.NoFood <- max(X.NoFood, Xcritical)
Term1 <- Pbenefit*F.vectors[X.Food,2] # If food is found
Term2 <- (1-Pbenefit)*F.vectors[X.NoFood,2] # If food is
not found
W <- (1 - Pmortality)*(Term1 þTerm2) # Survival in patch
return(W) # Return Fitness
} # End of function
# ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ....
# Function to iterate over patches
OVER.PATCHES <- function(X, F.vectors, Xcritical,Xmax, Xmin,
Npatch, Cost, Benefit, Pbenefit, Pmortality)
DYNAMIC PROGRAMMING 349
{
RHS <- matrix(0,Npatch,1) # Pre-allocate Right Hand Side of equn
for (i in 1: Npatch) # Cycle over patches
{
# Call Fitness function
RHS[i] <- FITNESS(X, Xcritical, Xmax, Xmin, Cost, Benefit[i],
Pbenefit[i], Pmortality[i], F.vectors)
} # End of i loop
# Now find optimal patch Best row is in Best[1]
Best <- order(RHS, na.last¼TRUE, decreasing¼TRUE)
F.vectors[X,1] <- RHS[Best[1]]
Best.Patch <- Best[1]
# Concatenate F(x,t) and the optimal patch number
Temp <- c(F.vectors[X,1], Best.Patch)
# Add Temp to bottom of F.vectors and rename to Temp
Temp <- rbind(F.vectors, Temp)
return (Temp)
} # End of function
# ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ....
# Function to iterate over states of X
OVER.STATES <- function(F.vectors, Xcritical, Xmax, Xmin,
Npatch, Cost, Benefit, Pbenefit, Pmortality)
{
Store <- matrix(0,Xmax,2) # Create matrix for output
for ( X in Xmin : Xmax) # Iterate over states of X
{
# For given X call Over.Patches to determine F(x,t) and best patch
Temp <- OVER.PATCHES(X, F.vectors, Xcritical, Xmax, Xmin,
Npatch, Cost, Benefit, Pbenefit, Pmortality)
# Extract components. Last row is F(x,t) and best patch
n <- nrow(Temp)-1
F.vectors <- Temp[1:n,]
Store[X,] <- Temp[nþ1,] # Save F(x,t) and best patch
} # End of X loop
# Add Store values to end of F.vectors for pass back to main program
Temp <- cbind(F.vectors, Store) # Combined by columns
return(Temp) # Return F.vectors and Store
} # End of function
# ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ....
# MAIN PROGRAM
# Initialize parameters
Xmax <- 10 # Maximum value of X
Xcritical <- 3 # Value of X at which death occurs
Xmin <- Xcriticalþ1 # Smallest value of X allowed
Cost <- 1 # Cost per period
Pmortality <- c(0, 0.004, 0.02) # Probability of mortality
Pbenefit <- c(1, 0.4, 0.6) # Probability of finding food
350 MODELING EVOLUTION
Benefit <- c(0, 3, 5) # Benefit if food is discovered
Npatch <- 3 # Number of patches
Horizon <- 20 # Number of time steps
# Set up matrix for fitnesses
# Column 1 is F(x, t). Column 2 is F(x,tþ 1)
F.vectors <- matrix(0, Xmax,2) # Set all values to zero
F.vectors[Xmin:Xmax,2] <- 1 # Set values > Xmin equal 1
# Create matrices for output
FxtT <- matrix(0,Horizon,Xmax) # F(x,t)
Best.Patch <- matrix(0,Horizon,Xmax) # Best patch number
# Start iterations
Time <- Horizon # Initialize Time
while ( Time > 1)
{
Time <- Time -1 # Decrement Time by 1 unit
# Call OVER.STATES to get best values for this time step
Temp <- OVER.STATES(F.vectors, Xcritical, Xmax, Xmin,
Npatch, Cost, Benefit, Pbenefit, Pmortality)
# Extract F.vectors
TempF <- Temp[,1:2]
# Update F1
for ( J in Xmin: Xmax) { F.vectors[J,2] <- TempF[J,1]}
# Store results
Best.Patch[Time,] <- Temp[,4]
FxtT[Time,] <- Temp[,3]
} # End of Time loop
# Output information. For display add states (¼wts) to last row of
matrices
X <- seq(from¼1, to¼Xmax)
Best.Patch[Horizon,] <-X
FxtT[Horizon,] <-X
Best.Patch[,Xmin:Xmax] # Print Decision matrix
signif(FxtT[,Xmin:Xmax],3) # Print Fxt of Decision matrix: 3
sig places
OUTPUT:
See Table 6.1.
MATLAB CODE: See Section 6.9.1.
6.1.5 Using the decision matrix: individual prediction
From Table 6.1 it can be seen that an animal that starts in a low state is forced to
take risks, whereas an animal that starts in a high state plays it safe. This behavior
is intuitively obvious but it is not obvious what parameter values will induce the
DYNAMIC PROGRAMMING 351
different behaviors: the decision matrix makes this clear. Most importantly, dy-
namic programming can show what behaviors will never be favored given a set of
parameter values and also the pattern of changes. The pattern of changes in the
present example is, as noted, intuitively obvious but, as further examples will
show, this is not always the case.
Having created the decision matrix we would now want to explore the actual
sequence of behaviors. To do this we run the model forward, as shown by the
coding given below. There are two instances in which a probability has to be
evaluated: Pmortality and Pbenefit. In each case, a random number between
0 and 1 is generated: If the value of this number is less than the value of the
parameter, then the action specified by the parameter is taken. For example,
suppose Pmortality ¼ 0.02 and the random number generated equals 0.01:
in this case the animal dies. Now suppose the random number generated equals
0.4: in this case the animal survives.
R CODE:
The coding assumes that the decision matrix has been generated. It is only
necessary to generate the matrix once by running the previous program.
Provided the command to clear the workspace is not issued the matrix will
remain in memory and the following program or variations can be run
successively:
# Initialize parameters
set.seed(10) # Set random number seed
Xmax <- 10 # Maximum value of X
Xcritical <- 3 # Value of X at which death occurs
Xmin <- Xcriticalþ1 # Smallest value of X allowed
Cost <- 1 # Cost per period
Pmortality <- c(0, 0.004, 0.02) # Probability of mortality
Pbenefit <- c(1, 0.4, 0.6) # Probability of finding food
Benefit <- c(0, 3, 5) # Benefit if food is discovered
Npatch <- 3 # Number of patches
Horizon <- 15 # Number of time steps
Output <- matrix(0,Horizon,10) # Matrix to hold output
Time <- seq(1, Horizon) # Values for x axis in plot
par(mfrow¼c(5,2)) # Divide graph page into 5x2 panels
for (Replicate in 1: 10) # Iterate over 10 replicates
{
X <- 4 # Animal starts in state 4
for (i in 1:Horizon) # Iterate over time
{
if(X > Xcritical) # Check that animal still alive
{
Patch <- Best.Patch[i,X] # Select patch
# Check if animal survives predation
# Generate random number
352 MODELING EVOLUTION
if(runif(1) < Pmortality[Patch]) print(“Dead from predator”)
# Now find new weight
# Set multiplier to zero, which corresponds to no food found
Index <-0
if (runif(1) < Pbenefit[Patch]) Index <- 1 # food is discovered
X <- X - Cost þ Benefit[Patch]*Index
# If X greater than Xmax then X must be set to Xmax
X <- min(X, Xmax)
# If X less than X then animal dies
if( X< Xmin) print(“Dead from starvation”)
Output[i,Replicate] <- Patch # Store data
} # End of if(X > Xcritical)
} # End of time loop
plot(Time, Output[,Replicate], type¼‘l’, ylab¼‘Patch selected’)
} # End of replicate loop
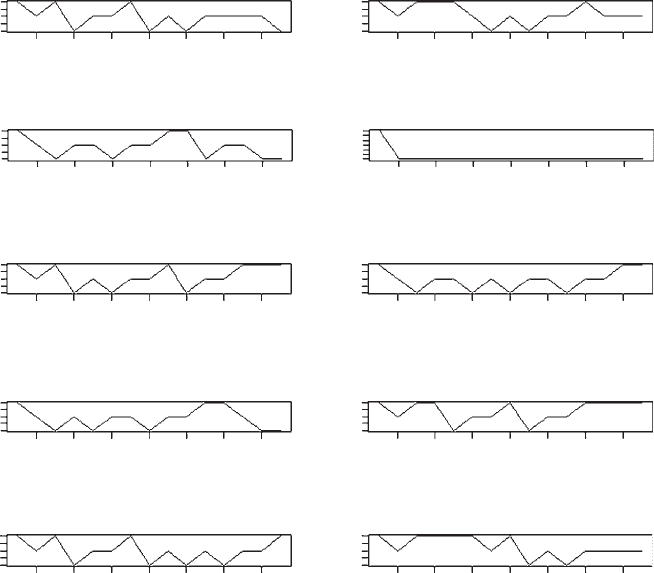
OUTPUT: (Figure 6.1)
Time
2
1.0
Patch selected
3.0
1.0
Patch selected
3.0
4 6 8 10 12 14
Time
2 4 6 8 10 12 14
0.0
Patch selected
3.0
Time
2 4 6 8 10 12 14
1.0
Patch selected
3.0
Time
2468101214
1.0
Patch selected
3.0
Time
2468101214
1.0
Patch selected
3.0
Time
2 4 6 8 10 12 14
1.0
Patch selected
3.0
Time
2 4 6 8 10 12 14
1.0
Patch selected
3.0
Time
2 4 6 8 10 12 14
1.0
Patch selected
3.0
Time
2468101214
1.0
Patch selected
3.0
Time
2 4 6 8 10 12 14
Figure 6.1 Output from running simulations using the decision matrix shown in Table
6.1, with a starting initial state of X =4.
DYNAMIC PROGRAMMING 353

In one case the animal died from starvation by the second time unit, but in all
other cases the animal survived the full period. There is considerable movement
between patch types, which could not be predicted without the dynamic program
solution.
MATLAB CODE: See Section 6.9.2.
6.1.6 Using the decision matrix: expected state
The traces shown in Figure 6.1 might indicate the outcome of an experiment in
which one is individual is followed 10 times or 10 individuals are followed once. To
ascertain the distribution of states we could run this program many times using
different starting inputs. However, we can more readily compute the expected
distribution of states using the following approach: We begin by asking “Given that
an animal is in state z at t 1, what is the probability that following the optimal
behavior it moves into state x at time t?” Mangel and Clark (1988) refer to this as the
transition density and using their mathematical symbolism it is written as
wðx; tjzÞ. Next we can calculate the probability that the animal will be in state x at
time t, P(x, t), by summing over all z values weighted by their representation in the
initial population (i.e., time t 1): in the notation of Mangel and Clark
Pðx; tÞ¼
X
z
wðx; tjzÞPðz; t 1Þð6:8Þ
If there is only a single animal or all animals commence in the same state, say z *,
then Pðz; t 1Þ¼Pðz
; t 1Þ¼1.
To calculate the transition density matrix we proceed as follows: Using the
decision matrix we select x given z: for each transition, provided z is greater
than Xcritical, there are four possible outcomes, with the subscript i designating
the best choice from the decision matrix (Table 6.2). To calculate the transition
density matrix we begin with an N N matrix, where N is the number of possible
states (in this case N would be Xmax – Xcritical þ 1), filled with zeros. If an animal
does not survive, then its state is set at Xcritical and the probability inserted in this
cell. Next we iterate across all possible values of z (i.e., Xmin z Xmax) and for
Table 6.2 Transition densities for the simple foraging model
Food
found
x
>Xcritical Survives xw(x,t|z)
Yes — Yes min(z – Cost + Benefit
i
,
Xmax)
(1 – Pmortality
i
)Pbenefit
i
....................................................................................................................................................
No Yes Yes z – Cost (1 – Pmortality
i
)(1 –Pbenefit
i
)
....................................................................................................................................................
No Yes No Set at Xcritical Pmortality
i
....................................................................................................................................................
No No — Set at Xcritical Pmortality
i
+(1– Pmortality
i
)
(1 – Pbenefit
i
)
Note: The source of mortality may be anything other than being less than Xcritical.
354 MODELING EVOLUTION
each value of z we calculate wðx; tjzÞusing the rules given in Table 6.2. Note that we
enter the decision matrix at the appropriate time, because the transition density
function is a function of the current state.
R CODE:
Because Xcritical is close to zero it is convenient to make the transition density
matrix here go from zero to Xmax, thus making each row and column correspond
to the value of x, as in the decision matrix. In the program below the rows
correspond to z and the columns to x. Because we want to use the decision
matrix, the workspace is not cleared. The decision matrix program is first run
and then the following:
# Set initial parameter values
Xmax <- 10 # Maximum value of state
Xcritical <- 3 # Critical value of state
Xmin <- Xcriticalþ1 # Lowest value of state
Cost <- 1 # Metabolic cost
Time <- 2 # Current state to be considered
Npatch <- 3 # Npatch is number of patches
Pmortality <- c(0, 0.004, 0.02)# Probability of mortality Beta
Pbenefit <- c(1, 0.4, 0.6) # Probability of finding food
Lambda
Benefit <- c(0, 3, 5) # Benefit if food is discovered Y
# Set transition density matrix to zero
Trans.density <- matrix(0, Xmax, Xmax)
# Step 1 Cycle over all values of z from Xmin to Xmax
for ( z in Xmin : Xmax) # Iterate over states
{
# Select the best patch from the Decision matrix at row Time
K <- Best.Patch[Time,z] # Decision matrix is called Best.Patch
# Calculate w(x,t|z)
# Found food and survives predator
x <- min(z - Cost þ Benefit[K], Xmax)
# Assign probability
Trans.density[z,x]<- (1-Pmortality[K])*Pbenefit[K]
# Food not found
x <- z - Cost
# State exceeds the critical value
if(x > Xcritical)
{
# Animal survives
Trans.density[z,x]<- (1-Pmortality[K])*(1-Pbenefit[K])
# Animal does not survive
Trans.density[z,Xcritical]<-
Pmortality[K]
} # end of if statement
# State is less than critical
DYNAMIC PROGRAMMING 355

else{ # Note that in R the { immediately follows else
Trans.density[z,Xcritical]<- Pmortality[K]þ(1-Pmortality[K])*
(1-Pbenefit[K])
} # End of else statement
} # end of z loop
Trans.density # Write out matrix
OUTPUT: (Table 6.3)
For this particular example the transition density matrix remains the same for all
times less than 13. Consider an animal (or population) commencing in state 4: it
will move to state 8 with a probability of 0.588 (or 58.8% of the population will be
in state 8), while there is a 0.412 probability that the animal will die (arbitrarily set
into state 3, Xcritical, which ensures no further progress). For an animal commenc-
ing in state 5 there is 0.02 probability of dieing, a 0.392 probability of passing into
state 4, and a 0.588 probability of passing into state 9 (Table 6.3).
MATLAB CODE: See Section 6.9.3.
6.1.7 Using the decision and transition density matrices to get expected
choices
The forgoing analyses determine the expected state an animal (or population) will
be in after some time steps. Of particular interest is the distribution of choices, as
this is what an experimenter will likely measure. To illustrate how these values
are calculated let us assume that at time t ¼ 2 our population is distributed among
the states, from x ¼ 4tox ¼ 9 as follows: 0.1, 0.1, 0.2, 0.3, 0.2, and 0.1, respectively.
Table 6.3 Transition density matrix for foraging model at time t = 2
Values of x
Values of z [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,] 0 0 0 0 0 0 0 0 0 0
....................................................................................................................................................
[2,] 0 0 0 0 0 0 0 0 0 0
....................................................................................................................................................
[3,] 0 0 0 0 0 0 0 0 0 0
....................................................................................................................................................
[4,] 0 0 0.412 0 0 0 0 0.588 0 0
....................................................................................................................................................
[5,] 0 0 0.02 0.392 0 0 0 0 0.588 0
....................................................................................................................................................
[6,] 0 0 0.02 0 0.392 0 0 0 0 0.588
....................................................................................................................................................
[7,] 0 0 0.02 0 0 0.392 0 0 0 0.588
....................................................................................................................................................
[8,] 0 0 0.004 0 0 0 0.5976 0 0 0.3984
....................................................................................................................................................
[9,] 0 0 0.004 0 0 0 0 0.5976 0 0.3984
....................................................................................................................................................
[10,] 0 0 0 0 0 0 0 0 0 0
Note: Each cell gives the probability, given that an animal is in state z at time t −1, that by
following the optimal behavior it moves into state x at time t. Output from R program is slightly
modified for display purposes.
356 MODELING EVOLUTION

Calculations are shown in Table 6.4. The optimal patch choice (“Best Patch” in Table
6.4) for each state is obtained from the decision matrix (Table 6.1) and the transition
probabilities (P(x, t) in Table 6.4) are obtained from the transition density matrix
(Table 6.3). In the present example two patches are expected to be chosen, patches
2 and 3. Assuming that animals that die are not counted (if they are counted then
column x ¼ 3 is included in subsequent calculations) the predicted proportions
are calculated by summing across rows from x ¼ 4tox=10, multiplying each cell by
P(z,t 1) as shown in the penultimate column of Table 6.4, and then correcting for
the loss of animals by dividing by the sum of this column, as shown in the
last column of Table 6.4. Finally, the proportion in each patch is calculated by
summing the probabilities for the individual patches. Thus, in the present example
68.4% of animals are expected to be found in patch 3 and 31.6% in patch 2.
6.1.8 Adjusting state values to correspond to index values
In the example considered the state values corresponded to the index values,
namely the positions in the relevant matrices (thus Xcritical ¼ 3 is both the critical
value and the cell index). This will generally not be the case and we have to
transform between state and index values. An example is shown in Table 6.5:
the lowest state (0.1–0.3 with midpoint 0.2) is assumed to be the “dead” state, that
is, Xcritical. The lowest state we assign to the first index (1) and then increment in
unit steps, the index value is then determined from
Index ¼ 1 þ
x Xcritical
Xinc
ð6:9Þ
where Xinc is the increment (0.2 in Table 6.5). Conversion from the index value to
state X is obviously
x ¼ðIndex 1ÞXinc þ Xcritical ð6:10Þ
Examples of the use of these transformations are given in Scenarios 3–5.
6.1.9 Linear interpolation to adjust for non-integer state variables
Dynamic programming works with discrete values but state variables may change
by amounts not equal to the assigned interval as described in the previous section.
For example, suppose the increments are 1 and states x ¼ 5 and x ¼ 6 correspond
to index values 6 and 7 (because the first cell is reserved for Xcritical) but for
some value of x with index value I the new state variable is 5.36, meaning
that the fitness lies between F(6, t) and F(7, t). To estimate F(x, t) we can use linear
interpolation (Figure 6.2; Mangel, personal communication). To derive the formu-
la we translate the origin of the x-axis to x
I
and the y-axis to F(x
I
, t) giving the slope
of the linear interpolation to be (Figure 6.2)
Fðx
Iþ1
; tÞFðx
I
; tÞð6:11Þ
DYNAMIC PROGRAMMING 357
