Roff D.A. Modeling Evolution: An Introduction to Numerical Methods

Подождите немного. Документ загружается.

print(c(i, mean(Data))) # Time, Output mean clutch size

Data <- table(Data) # Tabulate data

# Plot data using a bar graph, because x is integral

barplot(Data, xlab¼“Clutch Size”, space¼0, xlim¼c(0,5), main ¼

paste(“Time ¼ ”,i), col¼1)

}

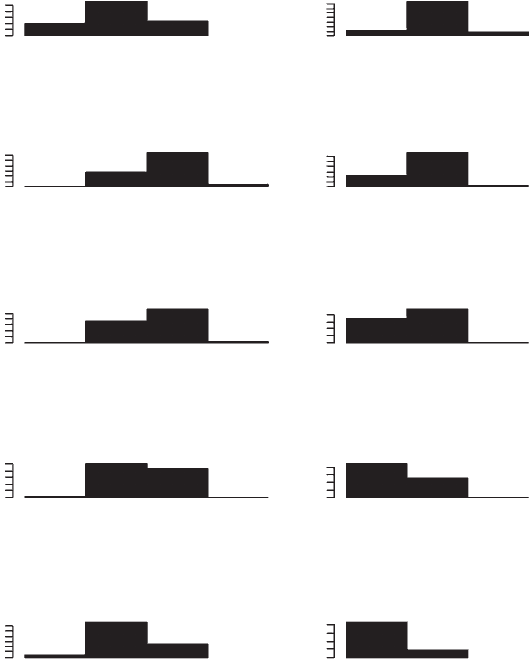
OUTPUT: (Figure 6.7)

Clutch Size

Time = 5 Time = 10

0 500

Clutch Size

0 400

Time = 9

Clutch Size

0 400

Time = 8

Clutch Size

0 400

Time = 7

Clutch Size

500

Time = 6

Clutch Size

600

Time = 1

Clutch Size

400

Time = 2

Clutch Size

500

234

Time = 3

Time = 4

Clutch Size

500

234

Clutch Size

0 400

234

Figure 6.7 Bar graphs of clutch size over time using the decision matrix to predict

oviposition behavior.

388 MODELING EVOLUTION

[1] 1.000000 3.036

[1] 2.000000 2.774619

[1] 3.000000 2.626927

[1] 4.000000 2.444906

[1] 5.000000 2.216842

[1] 6.000000 1.965921

[1] 7.000000 1.779978

[1] 8.000000 1.588661

[1] 9.000000 1.362360

[1] 10.00000 1.172745

The bar graphs (Figure 6.7) show an initial variation for clutch sizes from 2–4,

with

a diminishing of the mean size over time (see means above). This reduction

is due to the female running out of eggs. If females were prevented from laying

eggs, we would expect that the mean clutch size would increase. To test this

prediction I commenced the simulation at time 16, essentially preventing the

simulated females from laying any eggs until this time. The mean clutch sizes

still show the same decrease over time (4.64, 4.38, 4.16, 3.85, and 3.55), but the

proportion of females laying larger clutches increases (e.g., at t ¼ 16 no females

layaclutchsizeof9eggsbutsomedosoatt ¼ 30, Figure 6.8). For a fuller

discussion of this model see Mangel and Clark (1988, chapter 4).

MATLAB CODE: See Section 6.9.7.

6.7 Scenario 5: Optimizing egg and clutch size: dealing

with two state variables

Thus far we have assumed only a single state variable: however, there may be

many circumstances in which there are multiple state variables. In this scenario

we shall examine an extension of the previous scenario in which ﬁtness depends

upon both egg size and egg number. To better focus upon the method of dealing

with two state variables the previous scenario is somewhat simpliﬁed.

6.7.1 General assumptions

1. The animal commences the time period with some ﬁxed quantity of resources

that can be divided into clutches and eggs of different sizes. Thus although we

have two state variables, egg size, and clutch size, these can be combined

operationally into a single variable, reproductive biomass X.

2. Patches or hosts vary in quality.

3. The survival and growth of larvae depend on the number in the clutch, egg size,

and host quality.

4. Variation in host quality can be detected by the ovipositing females.

DYNAMIC PROGRAMMING 389

5. Survival of the female may or may not change over time. For computational

simplicity, I shall assume that the sequence of events is that egg-laying precedes

the determination of survival over the time period.

6. One host is encountered per time interval.

7. Hosts already with eggs are not encountered.

8. Fitness is a function of the number and size of offspring.

Clutch Size

Time = 20

0 250

2345678910

Clutch Size

Time = 18

0 200

23456789

Clutch Size

Time = 17

0 250

23456789

Clutch Size

Time = 16

0 200

23456789

Clutch Size

Time = 19

0 250

2345678

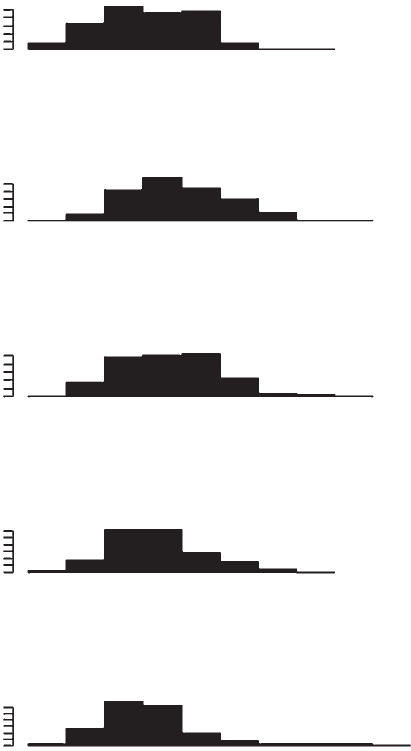
Figure 6.8 Bar graphs of clutch size over time using the decision matrix to predict

oviposition behavior when females are not allowed to oviposit until t = 16.

390 MODELING EVOLUTION

6.7.2 Mathematical assumptions

1. There are two types of host.

2. The amount of reproductive biomass available at time t is B

which is equal to

the product of egg size and clutch size,

¼ x

ð6:29Þ

where x

is the egg size and x

is the clutch size.

3. The single host ﬁtness can be modeled by the function

Benefit

i;E;C

¼ W

max;i



ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

E;i

ðx

 b

E;i

þ a

C;i

ðx

 b

C;i

ð6:30Þ

where the subscript i refers to host type and the coefﬁcients W

max;i

; a

E;i

; a

C;i

; b

E;i

; b

C;i

vary according to host type. The maximum beneﬁt on host type i is W

max,i

and is

obtained when egg size equals b

E,i

and clutch size is b

c,i

. Parameter values used in

this example are

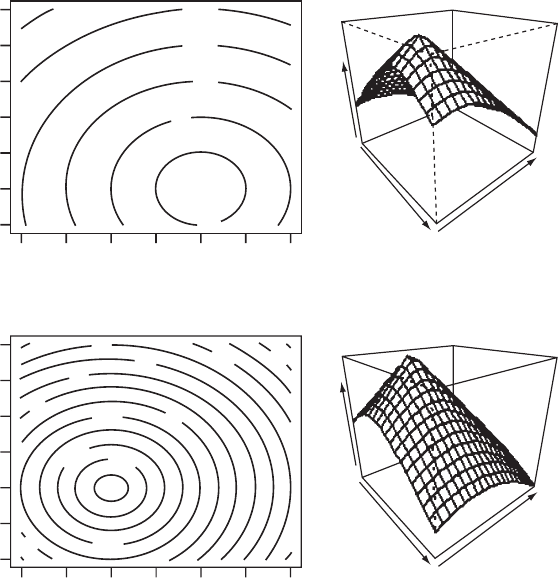
Thus on host type 1 the single host optimum is a larger egg size but smaller clutch

size than is optimal on host type 2 (Figure 6.9). The parameter space (i.e., combi-

nation space) over which ﬁtness is positive is small on host type 1 but relatively

large on host type 2.

4. A host is encountered during each time step: the probability of encountering

host type 1 is P

¼ 0.5 and hence the probability of encountering host type 2 is

¼ 1  P

¼ 0.5.

5. We shall assume a constant mortality per unit time, Pmortality ¼ 0.1. At the end

of the season no further eggs can be laid, meaning that the female is, from the

point of view of natural selection, dead. For computational simplicity we shall

use Psurvival ¼ 1  Pmortality. Thus

Psurvival ¼

0:90 for t<T1

0:00 for t ¼ T  1



ð6:31Þ

6. Overall ﬁtness is the sum of the ﬁtness increments obtained from each host.

6.7.3 Outcome chart and expected lifetime ﬁtness function

As in the previous example, an important feature of this model that differentiates

it from Scenarios 1–3 is that the value of the state variable increases as we move

toward t ¼ 1, rather than decreasing. Because no eggs are laid beyond time T, the

terminal ﬁtness is F(x, T) ¼ 0. Because eggs are laid prior to the calculation of

Host W

max

1 10 100 1 2 5

...................................................................................................................................................

2 20 100 1 1 10

DYNAMIC PROGRAMMING 391

size, x

Clutch size, y

0.0

Clutch size, y

0.5 1.0 1.5 2.0 2.5 3.0

Egg size, x

0.0 0.5 1.0 1.5

–2

–6

Fitness, W

Egg size, x

Clutch size, y

–5

–10

–15

2.0 2.5 3.0

Figure 6.9 Single host ﬁtness surfaces for Scenario 5. R code to produce graph is

rm(list=ls()) # Remove all objects from memory

# Function to calculate fitness, passing parameters to it

FITNESS <- function(X, Wmax, Xegg, Xclutch, ax, ay)

{

W <- Wmax-sqrt(ax*(X[1]-Xegg)^2 + ay*(X[2]-Xclutch)^2)

}

# MAIN PROGRAM

# Parameter values

Wmax <- c(10,20); Xegg <- c(2,1); Xclutch <- c(5,10); ax <-

100; ay <- 1

n <- 20 # Number of intervals for egg and clutch sizes

x <- seq(from=0, to=3, length=n) # Generate egg sizes

y <- seq(from=0, to=30, length=n) # Generate clutch size

d <- expand.grid(x,y) # Expand to all combinations

# Set plotting page to put graphs side by side and not distorted

# Make plotting surface consist of four panels

par(mfrow=c(2,2))

for ( i in 1:2)

392 MODELING EVOLUTION

survival, even if the female does not survive, the state variable takes a positive

value. Thus at each time step there is only one possible outcome, a host is found.

Because the model assumes that a host is encountered each time step the ﬁtness

function is somewhat simpler than in the previous scenario. The ﬁtness incre-

ment for each combination of host type i, egg size x

E,i

, and clutch size x

C,i

i;E;C

¼ Benefit

i;E;C

þ 0:90  Fðx  x

E;i

C;i

; tÞð6:32Þ

The term x  x

E;i

C;i

is unlikely to be an index and hence interpolation is neces-

sary. Note that the egg–clutch size combinations are restricted to those values less

than or equal to x

, the size of the state variable at time i. Clutch sizes must be

integer, but egg sizes are continuous. For each clutch size we ﬁnd the egg size that

maximizes F

i,E,C

and then compare different clutch sizes to get the global maxi-

mum, F

i,max

. Fitness for state variable x at time t  1 is given by

Fðx; t  1Þ¼P

1;max

þð1  P

ÞF

2;max

ð6:33Þ

6.7.4 Calculating the decision matrix

Unlike the previous scenario it is better to place the calculation of ﬁtness in a

separate function called FITNESS, as was done in Scenarios 1–3. Two features of

note in the programming of this scenario is the relatively extensive bookkeeping

that is necessary and the use of interpolation. While it could be possible to place

the output in a single array I prefer to make separate matrices, because the coding

is clearer. The program runs in the following sequence:

Step 1: Input parameter values and the 7 matrices for storing the following

output: the state value (FxtT), the optimal clutch sizes for the two hosts (Best.

{

# Create a vector of fitness values for all combinations

Wtemp <- apply(d,1, FITNESS,Wmax[i], Xegg[i],Xclutch[i],ax,ay)

# Convert into matrix

W <- matrix(Wtemp,n,n,byrow=F)

# Plot contour. las=orientation of axis labels

# lwd= line width, labcex=size of contour labels

contour(x,y,W, xlab=‘Egg size, x’, ylab=‘Clutch size,y’, las=1,

lwd=3, labcex=1)

#Plot perspective plot

persp(x,y,W,xlab=‘Egg size, x’, ylab=‘Clutch size, y’, zlab=‘Fit-

ness, W’,theta = 50, phi = 25,lwd=2)}

Host found Survives X

Yes Yes x‐Beniftit

iE,C

.................................................................................................

Yes No x‐Beniftit

iE,C

DYNAMIC PROGRAMMING 393

Clutch1, Best.Clutch2), the optimal egg sizes for the two hosts (Best.Egg1,

Best.Egg2), and two matrices indicating whether there are at least two choices

of maximal ﬁtness for a given host type (Choice.H1, Choice.H2, 1 will signify a

single optimum and 2 that there are at least two optima).

Step 2: Iterate over time.

Step 3: Call the function OVER.STATES to iterate over values of the state variable.

This function is the same as in the previous scenario except that the number of

columns in the storage matrix Store is increased to 7 to hold the increased

number of output variables.

Step 4: Call the function OVER.PATCHES to calculate the optimum decision over

host types for the given value of the state variable. Iterate over each host (patch)

and for each do the following.

Step 5: Create a 3  11 matrix to store the ﬁtness for the optimum egg size at a

given clutch size.

Step 6: Iterate over clutch sizes from 1 to 11.

Step 7: Pass the function FITNESS to optimize to ﬁnd the optimal egg size.

Step 8. In FITNESS the following steps are applied:

Step 8a : Calculate the reproductive biomass for this combination (¼Biomass).

Step 8b: Check that this is a permissible biomass in that it is less than the present

value of the state variable X. If this test is not passed then set ﬁtness W to zero and return.

Step 8c: If step 8b is passed ﬁrst calculate F(x, t). Because the index value of

Biomass may not be an integer interpolation is used, the interpolated value being

designated Fxt.interpolated.

Step 8d: Calculate the ﬁtness on the given host using equation (6.30). Set to zero

if negative.

Step 8e: Calculate ﬁtness using equation (6.32) and return.

Step 9: Store ﬁtness, clutch size, and egg size in W.host.

Step 10: After iteration over clutch sizes is completed ﬁnd the combination with

the highest ﬁtness. Store in Best.in.Patch. Test if “second-best” combination

has the same ﬁtness as the “best”: if so store result as 2 in matrix Choice.Flag.

Step 11: After iterating over both hosts calculate the ﬁtness using equation (6.33).

Step 12: Concatenate the vector F.vectors with the relvant output information

and pass back to OVER.STATES where it is stored and a new state value is passed

to OVER.PATCHES.

Step 13: After iterating over patches, state values, and time, output matrices.

R CODE:

To ensure that “interesting” results were obtained I set the state variable,

reproductive biomass, within a range, 1–10, over which the egg–clutch size

394 MODELING EVOLUTION

combinations for a single host cannot be achieved (a useful method of testing

that the model is performing correctly is to set the state variable so high that

the optimum combinations for the two hosts can be achieved).

rm(list¼ls()) # Remove all objects from memory

FITNESS <- function (Egg, Clutch, X, F.vectors, Xcritical, Xmax,

Xinc, Psurvival, Wmax, A, Xegg, Xclutch, Ith.Patch)

{

W <- 0 # Set fitness to zero

Biomass <- Clutch*Egg # Biomass of clutch/Egg size

combination

if( Biomass < X) # Continue only if Biomass < X

{

Max.Index <-1þ (Xmax-Xcritical)/Xinc # Get maximum index

value

# Index value for biomass

Index <-1þ(Biomass-Xcritical)/Xinc

# Get fitness at lower and upper integer value of Biomass

Index.lower <- floor(Index)

Index.upper <- Index.lower þ 1

# Must stop index exceeding Max.Index. Note that Qx ¼ 0 in this case

Index.upper <- min(Index.upper, Max.Index)

Qx <- Biomass - floor(Biomass)

Fxt.lower <- F.vectors[Index.lower,2]

# Get fitness at upper integer value of

Fxt.upper <- F.vectors[Index.upper,2]

Fxt.interpolated <- Qx*Fxt.upper þ(1-Qx)*Fxt.lower # Iterpolated

value

# Calculate the fitness for this particular egg-clutch size combi-

nation

W <- Wmax[Ith.Patch]-sqrt(A[1]*(Egg-Xegg[Ith.Patch])^2 þ A[2]*

(Clutch-Xclutch[Ith.Patch])^2)

W <- max(0, W) # Set to zero if negative

W <-Wþ Psurvival*Fxt.interpolated # Fitness

W <- max(0, W) # Set to zero if negative

} # End of if

return(W)

} # End of function

# ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ....

# Function to iterate over patches i.e. over Hosts

OVER.PATCHES <- function(X, F.vectors, Xcritical, Xmax, Xinc,

Npatch, Psurvival, Wmax, A, Xegg, Xclutch,P1)

{

X is the total biomass available Get index value for X

Index <-1þ(X-Xcritical)/Xinc

DYNAMIC PROGRAMMING 395

# Allocate storage of best combinations for each patch

# Columns will contain

# Fitness, Clutch, Egg

Choice.Flag <- matrix(0,2) # Store information on

number of choices

Best.in.Patch <- matrix(0,2,3) # Allocate storage for Best

Decision

# Iterate over patches

for ( Ith.Patch in 1:Npatch) # Iterate over the two hosts (¼

patches)

{

# Make a matrix called W.host with the following 3 columns:

# Fitness, Egg size, Clutch size

W.host <- matrix(0,11,3)

for ( Clutch in 1:11) # Iterate over clutch size

{

W.host[Clutch,2] <- Clutch # Store clutch size

# Call optimize to find best egg size

B <- optimize(f ¼FITNESS, interval ¼c(0.01,3),Clutch, X,F.vec-

tors, Xcritical, Xmax, Xinc, Psurvival, Wmax, A, Xegg, Xclutch,

Ith.Patch, maximum¼TRUE)

W.host[Clutch,1] <- B$objective # Fitness

W.host[Clutch,3] <- B$maximum # Egg size

} # End of clutch size loop

# Get best combination for this host

R <- W.host[,1]

Best <- order(R, na.last¼TRUE, decreasing¼TRUE)

Best.in.Patch[Ith.Patch,] <- W.host[Best[1],] # Store best

choice

# Test for several equal optimal choices

if(W.host[Best[1],1]¼¼W.host[Best[2],1])Choice.Flag[Ith.

Patch] <-2

} # Next host

# Overall fitness

W <- P1*Best.in.Patch[1,1] þ(1-P1)*Best.in.Patch[2,1]

F.vectors[Index,1]<- W # Update F(x,t,T)

# Concatenate F(x,t) and the optimal egg and clutch values for both

hosts

# We add to the bottom of the two column matrix F.vectors the

# following

# F.vectors[Index,1], 1 The second entry is simply a dummy variable

# Best.in.Patch[1,2] Best.in.Patch[1,3] # Host 1 Egg size Clutch

size

# Best.in.Patch[2,2] Best.in.Patch[2,3] # Host 2 Egg size Clutch

size

396 MODELING EVOLUTION

# Choice.Flag[1:2] # Flag for multiple optima

Temp1 <- c(F.vectors[Index,1], 1)

Temp2 <- c( Best.in.Patch[1,2], Best.in.Patch[1,3])

Temp3 <- c( Best.in.Patch[2,2], Best.in.Patch[2,3])

# Add Temp1, Temp2, Temp3 & Choice to bottom of F.vectors and rename

to Temp

Temp <- rbind(F.vectors, Temp1, Temp2, Temp3, Choice.Flag[1:2])

return (Temp)

} # End of function

# ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ....

# Function to iterate over states of X

OVER.STATES <- function(F.vectors, Xcritical, Xmax, Xinc,

Npatch, Psurvival, Max.Index, Wmax, A, Xegg, Xclutch, P1)

{

# Create matrix for output. Note that we use seven columns

Store <- matrix(0, Max.Index,7)

# Iterate over X ¼ Biomass X[1] is zero so skip

for ( Index in 2 : Max.Index) # Iterate over states of X

{

# For given X call Over.Patches to determine F(x,t) and best patch

X <- (Index-1)*Xinc þ Xcritical

Temp <- OVER.PATCHES(X, F.vectors, Xcritical, Xmax, Xinc,

Npatch, Psurvival,Wmax, A, Xegg, Xclutch, P1)

# Extract components. Last row-2 is F(x,t) and dummy variable

# Last row-1 is best clutch and egg size for host type 1

# Last row is best clutch and egg size for host type 2

# Last row is flage indicating multiple equal choices

n <- nrow(Temp)-4

F.vectors<- Temp[1:n,] # Extracting F.vectors

# Add the seven output values (omit dummy) to storage

Store[Index,] <- c(Temp[nþ1,1], Temp[nþ2,1:2], Temp[nþ3,1:2],

Temp[nþ4, 1:2])

} # End of X loop

# Add Store values to end of F.vectors for pass back to main program

Temp <- cbind(F.vectors, Store) # Combined by columns

return(Temp) # Return F.vectors and Store

} # End of function

# ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ....

# MAIN PROGRAM

# Initialize parameters

# Create the state variable (X¼reproductive biomass)

Xmax <- 10; Xcritical <- 0; Xinc <-1

Max.Index <-1þ (Xmax-Xcritical)/Xinc

# Parameter values on the two hosts

Wmax <- c(10, 20) # Maximum fitness

DYNAMIC PROGRAMMING 397