Родичев Ю.А. Компьютерные сети - архитектура, технологии, защита
Подождите немного. Документ загружается.

61
ные точки в U (т.е. кривая, непрерывно деформируемая в отрезок
с концами в этих точках).
Простой замкнутой кривой в U называется непрерыв-
ная самонепересекающаяся кривая, концевые точки которой сов-
падают (т.е. кривая, непрерывно деформируемая в окружность).
Пусть V={A
1
, А
2
, ...} – любое непустое (конечное или беско-
нечное) множество точек и Е={е
1
, е
2
,…} – любое множество про-
стых кривых в U, удовлетворяющих следующим трем условиям:
1. Каждая замкнутая кривая из Е содержит ровно одну точ-
ку из V;
2. Каждая незамкнутая кривая из Е содержит ровно две
точки из V, являющиеся ее граничными точками;
3. Кривые из Е могут пересекаться только в точках из V.
Рассмотрим отображение
f: Е→V&V, определяемое по сле-
дующему закону. Каждой незамкнутой кривой поставим в соот-
ветствие неупорядоченную пару ее граничных точек (сущест-
вующих по условию 2), а каждой замкнутой кривой сопоставим
пару, состоящую из дважды взятой точки, лежащей на этой кри-
вой (эта точка существует по условию 1). Тогда множество точек
V, множество кривых
Е и отображение f будут удовлетворять аб-
страктному определению графа.
Граф, состоящий из точек и простых кривых, удовлетворяю-
щих условиям 1 – 3, называется геометрическим графом.
Если элементы геометрического графа G (т.е. вершины и ребра)
лежат в плоскости (т.е. U – плоскость), то граф G называется
плоским графом, если же элементы графа G
лежат в про-
странстве, то граф G называется пространственным.
2.1.3. Инцидентность и смежность элементов графа
Определение инцидентности
Пусть задан абстрактный граф G(V, Е, f). Если отображение
инциденции f сопоставляет ребру е пару вершин (х
1
&х
2
), т.е. f(e)
= (х
1
&х
2
), то говорят, что ребро е инцидентно вершинам х
1
и х
2
.
Употребляют также следующие выражения: «ребро е соединяет
вершины x
1
и x
2
» или «вершины x
1
и x
2
являются граничными
точками ребра е». Если граничные точки ребра е совпадают, т.е.
62
f(е) = (x&x), то это ребро называется петлей в вершине х. Так,
например, ребро а на рис. 2.2 является петлей в вершине Н. Из
определения графа следует, что каждое ребро, не являющееся
петлей, может быть инцидентно ровно двум вершинам, являю-
щимся его граничными точками. Остальные вершины графа счи-
таются не инцидентными этому ребру
. Точно так же каждая пет-
ля графа инцидентна лишь одной своей вершине и не инцидентна
остальным вершинам графа. Для геометрического графа ребра, не
являющиеся петлями, соответствуют простым незамкнутым кри-
вым, а петли – простым замкнутым кривым.
Определение смежности
Две вершины x
1
и x
2
графа G(V, Е, f) называются смежны-
ми, если в графе существует ребро е, инцидентное этим верши-
нам. Вершина графа смежна самой себе в том и только том слу-
чае, если в графе существует петля с вершиной в этой точке. Дру-
гими словами, две вершины графа называются смежными, если
они инцидентны одному и
тому же ребру. Так, например, на рис.
2.2 вершины А и В являются смежными (их соединяет, в частно-
сти, ребро p), вершины С и Н – не смежны, а вершина Н – смежна
сама с собой.
Два ребра графа называются смежными, если существует
вершина, инцидентная обоим этим ребрам. Так, на рисунке 2.2
ребра f
и h являются смежными, так как они инцидентны верши-
не Н.
Два ребра графа называются параллельными, если они
инцидентны одним и тем же вершинам, т.е. если они соединяют
одну и ту же пару вершин. Так, например, на рис. 2.2 вершинам А
и В инцидентны три параллельных ребра p, l и d
. Ясно, что па-
раллельные ребра являются также и смежными.
Заметим, что отношение инцидентности связывает разнород-
ные элементы графа (вершины и ребра), а отношение смежности
– однородные элементы (либо вершины, либо ребра).
2.1.4. Степени вершин графа
Степенью вершины графа называется количество ин-
цидентных ей ребер (для петли степень подсчитывается дважды).
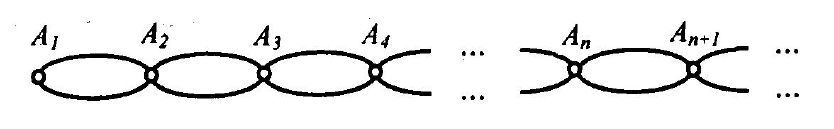
63
Через Q(x) будем обозначать степень вершины х. Для графа на
рис. 2.2 вершины имеют следующие степени:
Q(А) = 4, Q(В) = 6, Q(C) = 1, Q(D) = 0, Q(F) =Q(P) = 2, Q(Н) = 5.
Ясно, что степень любой вершины конечного графа есть целое
неотрицательное число. Вообще, определенное нами понятие
степени имеет смысл лишь для вершин, инцидентных конечному
числу ребер, при этом множество вершин и множество ребер
графа могут быть бесконечными. Так, на рис. 2.3 представлен
бесконечный граф, все вершины которого имеют степень 4 (кро-
ме первой вершины, имеющей степень 2). Этот граф моделирует
так называемые процессы «гибели-размножения».
Рис. 2.3. Бесконечный граф
Вершина графа степени 0 называется изолированной. Ес-
ли степень вершины равна 1, то она называется концевой или
висячей вершиной. Вершина, степень которой больше или
равна 2, называется промежуточной или проходной. Так,
на рис. 2.2 вершина D – изолированная, вершина С – висячая, а
остальные вершины – проходные.
Вершины графа называются четными или нечетными в
зависимости от четности их степеней. Так, в графе на рис. 2.3 все
вершины – четные. Граф на рис. 2.2 имеет две нечетные вершины
(С и H), а остальные вершины этого графа – четные.
Теорема 1. В любом конечном графе G(V, Е) количество
нечетных вершин – четно.
Действительно, каждое ребро добавляет по единице к степе-
ням своих
граничных вершин, а каждая петля добавляет двойку к
степени своей вершины. Поэтому сумма степеней всех вершин
равна удвоенному числу ребер графа:
∑ Q(x)=2|E| (1.4.1)
Здесь через |E| обозначено число элементов во множестве E,
т.е. количество ребер графа G. Формула 1.4.1 показывает, что
64
сумма степеней всех вершин графа есть четное число. Поэтому в
эту сумму может входить лишь четное количество нечетных сла-
гаемых, т.е. количество нечетных вершин графа G есть четное
число.
Следствие. Сумма степеней всех вершин конечного графа
равна удвоенному числу его ребер.
Граф называется элементарным, если он не содержит пе-
тель и параллельных ребер.
Элементарный конечный граф называется полным, если его
любая пара различных вершин соединена ребром. Полный граф с
N вершинами содержит (N-1)×N/2 ребер.
Граф называется однородным (регулярным) степе-
ни k, если все его вершины имеют одинаковую степень k. Одно-
родный граф нулевой степени называется нуль- графом или
пустым
графом. Он не имеет ребер и состоит только из изо-
лированных вершин. Однородный граф третьей степени называ-
ется кубическим графом. В силу теоремы 1, любой однород-
ный граф нечетной степени (в частности кубический граф) со-
держит четное число вершин. Полный граф с n вершинами явля-
ется однородным степени n-1, а полный граф
с петлями – одно-
родным степени n+1.
Задачи и упражнения
1. Докажите, что число перекрестков любого города, в кото-
рых встречается нечетное число улиц, четно.
2. У марсиан бывает произвольное число рук. Однажды все
марсиане взялись за руки так, что свободных рук не осталось.
Докажите, что количество марсиан с нечетным числом рук
четно.
3. Докажите, что число зрителей, пришедших на стадион
смотреть футбольный матч и имеющих нечетное число знакомых
(среди того же множества зрителей) четно.
4. Докажите, что число людей, когда-либо живших на Земле и
сделавших нечетное число рукопожатий, четно.
5. В классе 30 человек. Может ли быть так, что 9 из них име-
ют
по 5 друзей каждый, 11 – по 4 друга и 10 – по 3 друга?
6. В офисе 15 телефонов. Можно ли их соединить между со-
бой проводами так, чтобы каждый был соединен с 3 другими?
65
7. Можно ли нарисовать на плоскости 11 отрезков так, чтобы
каждый пересекался ровно с тремя другими?
8. В государстве 100 городов, и из каждого из них выходит по
4 дороги. Сколько всего дорог в государстве?
9. Может ли в государстве, в котором из каждого города вы-
ходит ровно по три дороги, быть 100 дорог?
10. На
радиостанции каждый радиоузел соединен ровно с 15
другими. Может ли быть число проводов на радиостанции равно
200?
Ответы и пояснения
Во всех задачах нужно смоделировать условия при помощи
графов. Задачи 1–7 решаются при помощи теоремы 1, а при реше-
нии задач 8–10 нужно использовать следствие из этой теоремы.
Доказательство утверждений в задачах 1–4 дословно повторя-
ет
доказательство теоремы 1.
В задачах 5–7 ответ отрицательный, так как ситуации, соот-
ветствующие условиям каждой из этих задач, противоречат тео-
реме 1.
7. Нужно рассмотреть граф, вершины которого соответствуют
отрезкам, а ребра соединяют вершины, которым соответствуют
пересекающиеся отрезки.
8. Рассмотрим граф G (V, Е), у которого множество вершин V
состоит из 100 городов, а множество ребер
Е состоит из всех до-
рог государства. По условию задачи каждая вершина этого графа
имеет степень 4. Применяя формулу (1.4.1), получим, что 4×100
= 2×|Е|. Следовательно, количество дорог |Е| равно 200.
9. Моделируя условие задачи так же, как в задаче 8, и приме-
няя следствие из теоремы 1, получим: 3×|V|=2×100. Так как
ко-
личество вершин |V| должно быть натуральным числом, то ответ
на вопрос задачи – отрицательный.
10. Ответ к задаче – отрицательный. Ее решение аналогично
решению задачи 9.
2.1.5. Изоморфизм графов
Два графа G и G
1
называются изоморфными (или рав-
ными), если между их однотипными элементами можно устано-
66
вить взаимно-однозначные соответствия, сохраняющие отноше-
ние инциденции.
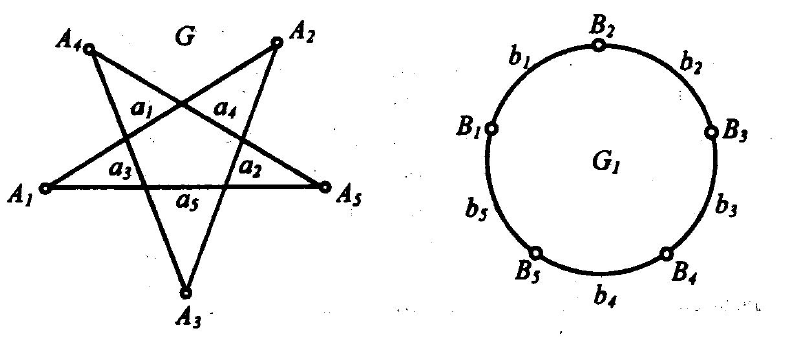
Пример. Рассмотрим два графа G и G
1
. изображенные на
рис. 2.4.
Рис. 2.4. Изоморфные графы
Граф G имеет множество вершин V={A
i
}, i = 1,2,3,4,5 и мно-
жество ребер Е = {a
i
} i=1,2,3,4,5, а граф G
1
состоит из множества
вершин V
1
={B
i
} i=1,2,3,4,5 и множества ребер Е
1
={b
i
} i=1,2,3,4,5.
Определим взаимно-однозначное соответствие I между элемен-
тами этих графов при помощи пары отображений I
1
:V→V
1
, и
I
2
:E→E
1
, заданных по формулам:
I
1
(A
i
)=B
i
; I
2
(a
i
)=b
i
Легко видеть, что две вершины графа G соединены ребром то-
гда и только тогда, когда соответствующие вершины графа G
1
со-
единены соответствующим ребром. Поэтому построенное взаим-
но однозначное соответствие I=(I
1
;I
2
) между элементами графов
G и G
1
сохраняет отношение инциденции. Таким образом, можно
утверждать, что графы G и G
1
изоморфны.
Описанное в примере взаимно однозначное соответствие
I=(I
1
;I
2
), состоящее из пары отображений I
1
и I
2
и обеспечиваю-
щее изоморфизм графов, называется отображением изо-
морфизма G на G
1
. Таким образом, граф G изоморфен графу
G
1
тогда и только тогда, когда существует отображение изомор-
физма G на G
1
. Для того чтобы доказать, что некоторые графы G
и G
1
изоморфны, нужно построить конкретное отображение изо-
морфизма (как в приведенном примере).
67
Из определения изоморфизма следует, что изоморфные графы
имеют одинаковое количество элементов. Вершины, соответст-
вующие при изоморфизме, имеют одинаковую степень. При ото-
бражении изоморфизма петли переходят в петли, а параллельные
ребра – в параллельные ребра. Вообще изоморфные графы имеют
одинаковые комбинаторные свойства и, с точки зрения теории
графов, неразличимы. В частности, изоморфизм графов
сохраня-
ет смежность вершин и смежность ребер.
Рассмотренное понятие важно в теории информационных се-
тей. Граф G можно рассматривать как топологию компьютерной
сети с устройствами (узлами) в вершинах A
1
, A
2
, A
3
, A
4
, A
5
, свя-
занными отрезками линий связи a
1
, a
2
, a
3
, a
4
, a
5
. На первый взгляд
каждый узел сети связан с соседними, образуя топологию типа
звезда. Граф G
1
наглядно показывает, что все узлы сети образуют
топологию логического кольца.
2.1.6. Части графа
Пусть задан некоторый конечный граф G(V, Е, f). Существует
ряд операций, называемых операциями разборки графа,
позволяющих из исходного графа получать новые графы, множе-
ства вершин которых являются подмножествами множества V, а
множества ребер – подмножествами множества Е. При этих опе-
рациях должно сохраняться отношение инцидентности, имеющее
место для исходного графа G, при выполнении
разумного требо-
вания о том, что множество вершин графа G
1
должно включать
все граничные точки множества его ребер. Существует два ос-
новных вида операций разборки графа G:
1) удаление ребра между двумя вершинами графа G с сохра-
нением граничных вершин;
2) удаление вершины графа G вместе со всеми ей инцидент-
ными ребрами.
Частным случаем второй операции разборки является операция
2 а) удаление
изолированной вершины графа G.
Ясно, что после применения конечного числа операций раз-
борки этих двух видов получится новый граф G
1
(V
1
, E
1
, f
1
), не
изоморфный исходному графу G(V, E, f).
68
Граф G
1
, полученный из графа G при помощи конечного чис-
ла операций разборки, называется частью графа G. В теории
графов представляют интерес два наиболее важных вида частей
графа – подграф и суграф. Подграфом графа G называется
такая его часть G
1
, которая получается из графа G при помощи
конечного числа операций разборки вида 2, т.е. – при помощи
удаления конечного числа вершин вместе со всеми примыкаю-
щими к ним ребрами. Граф G по отношению к своему подграфу
G
1
называется надграфом.
Суграфом графа G называется такая его часть G
1
, которая
получается из графа G при помощи конечного числа операций
разборки вида 1, т.е. – при помощи удаления конечного числа ре-
бер (с сохранением вершин). Граф G по отношению к своему су-
графу G
1
называется сверхграфом. Граф G по отношению к
произвольной своей части G
1
называется объемлющим графом.
Пример. Пусть G(V, Е) – это граф автомобильных дорог неко-
торого государства. Здесь V – множество всех городов этого го-
сударства, а Е – совокупность всех дорог между городами. Если
удалить из графа G все второстепенные дороги, то получим граф
главных дорог государства, который является суграфом графа G.
Рассмотрим
теперь некоторую губернию этого государства. Уда-
лим из графа G все города, не находящиеся на территории этой
губернии, вместе со всеми примыкающими к ним дорогами. В ре-
зультате получим граф автомобильных дорог этой губернии, яв-
ляющийся подграфом графа G.
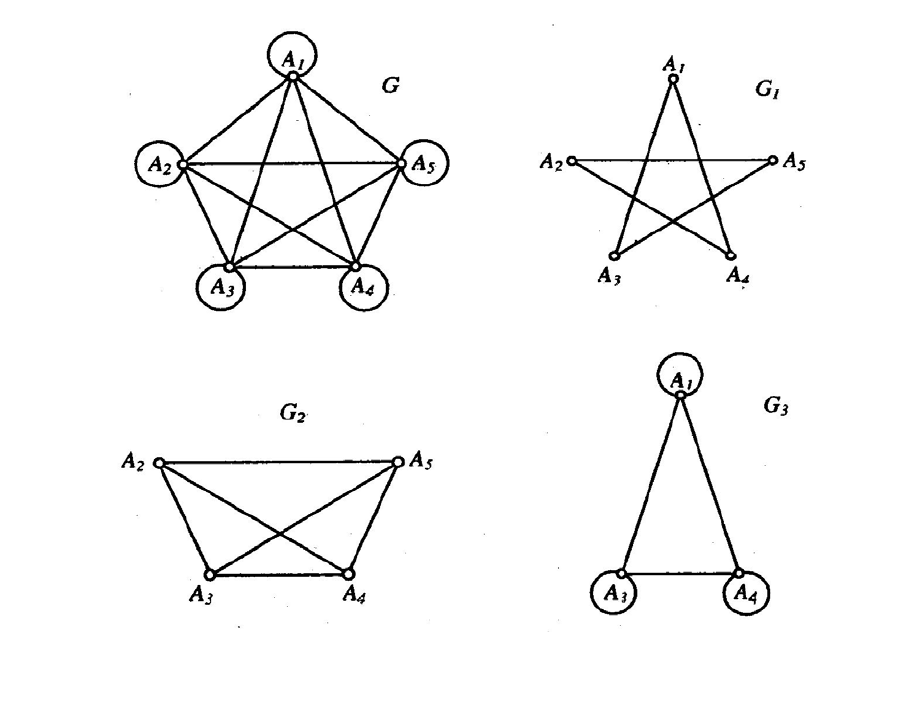
Упражнение
Докажите, что графы G
1
, G
2
и G
3
являются частями графа G
(см. рис. 2.5). Какие из этих графов являются подграфами и какие
– суграфами объемлющего графа G? Указать процессы разборки
графа G, приводящие к графам G
1
, G
2
и G
3
.
Ответы и пояснения
1. Граф G
1
может быть получен из графа G только при помо-
щи удаления ребер (т.е. с использованием операции разборки ви-
да 1). Эта операция применяется 10 раз при удалении следующих
ребер: A
1
&A
1
, A
2
&A
2
, A
3
&A
3
, A
4
&A
4
, A
5
&A
5
, A
1
&A
2
, A
2
&A
3
, A
3
&A
4
,
A
4
&A
5
, A
5
&A
1
. Следовательно, G
1
является суграфом графа G (а,
69
следовательно, – и частью этого графа). Граф G
2
может быть по-
лучен из графа G, например, при помощи следующих операций
разборки:
– удаление всех петель (пятикратное применение операции
разборки вида 1);
– удаление вершины А
1
вместе со всеми ей инцидентными
ребрами (операция разборки вида 2).
Таким образом, граф G
2
является частью графа G.
Граф G
3
может быть получен из графа G при помощи дву-
кратного применения операции разборки вида 2 (удаление вер-
шин А
2
и А
5
вместе со всеми инцидентными им ребрами). Следо-
вательно, G
3
– подграф графа G.
Заметим, что G – это полный граф с петлями, содержащий 5
вершин; G
1
– граф, изоморфный правильному пятиугольнику; G
2
– полный граф с 4 вершинами; G
3
– полный граф с петлями, со-
держащий 3 вершины.
Пополнением элементарного графа G называется его
сверхграф G
1
, являющийся полным графом. Граф G является су-
Рис. 2.5. Операции разборки графа

70
графом своего пополнения G
1
и получается из последнего при
помощи операции удаления ребер. Переход от графа G к его по-
полнению можно осуществить при помощи обратной операции,
называемой операцией добавления ребер. Каждая такая
операция увеличивает количество ребер графа на единицу, не ме-
няя числа вершин графа. Разность между количествами ребер
графов G
1
и G называется степенью неполноты графа G.
Рис. 2.6. Пополнение графа
Пример. На рис. 2.6 представлен элементарный граф G и его
пополнение G
1
. Добавляемые ребра изображены пунктиром, их
количество равно степени неполноты графа G.
2.1.7. Непрерывные последовательности
ребер графа
Пусть задан некоторый граф G. Каждое ребро этого графа
можно интерпретировать как связующее звено между двумя
смежными вершинами. Если зафиксировать некоторую вершину
графа и последовательно переходить по связующим ребрам из
вершины в вершину, то по прошествию конечного числа таких
переходов можно перейти в другую вершину или вернуться в ис-
ходную. В
геометрическом графе описанный процесс интерпре-
тируется как непрерывное движение по последовательности про-
стых кривых от одной вершины к другой. Опишем наиболее важ-
ные непрерывные последовательности ребер графа.
