Родичев Ю.А. Компьютерные сети - архитектура, технологии, защита
Подождите немного. Документ загружается.

71
Маршруты
Пусть граф G (V, Е, f) имеет не более чем счетные множества
вершин V={А
1
, А
2
,…, А
n
} и ребер E={a
1
, a
2
,…, a
n
}. Конечная по-
следовательность ребер графа a
1
, a
2
,…, a
k
(не обязательно раз-
личных) называется маршрутом длины k, если граничные точки
двух соседних ребер этой последовательности совпадают. Первая
и последняя вершины называются соответственно начальной и
конечной вершиной маршрута. Остальные вершины последова-
тельности называются промежуточными вершинами этого мар-
шрута. Также говорят, что маршрут a
1
, a
2
,…, a
k
соединяет вер-
шины А
1
, и А
k
.
Заметим, что любое ребро (или петля) является маршрутом
длины 1, соединяющим свои граничные вершины. Маршрут на-
зывается замкнутым, если его начальная и конечная вершины
совпадают. В противном случае маршрут называется незамк-
нутым.
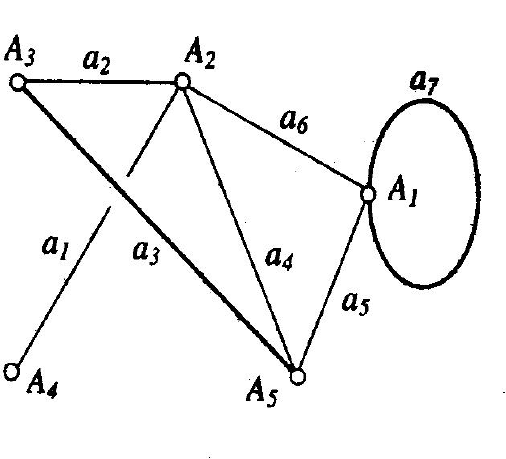
Рис. 2.7. Маршруты
Пример. На рис. 2.7 последовательность ребер a
1
,a
4
,a
5
,a
6
,a
2
,a
2
образует незамкнутый маршрут длины 6, соединяющий вершины
А
4
и А
2
, а последовательность ребер a
7
,a
6
,a
4
,a
5
,a
7
определяет не-
замкнутый маршрут длины 5, который начинается и заканчивает-
ся в вершине А
1
.
72
Цепи и циклы
Цепью называется незамкнутый маршрут, состоящий из по-
следовательности различных ребер. Замкнутый маршрут, со-
стоящий из последовательности различных ребер, называется
циклом. Так, маршрут a
1
,a
4
,a
5
,a
6
,a
2
на рис. 2.7 является цепью,
а замкнутый маршрут a
7
,a
6
,a
4
,a
5
представляет собой цикл. Заме-
тим, что маршрут a
1
,a
4
,a
5
,a
6
,a
2
,a
2
не является цепью, а замкнутый
маршрут a
7
,a
6
,a
4
,a
5
,a
7
не является циклом.
Частным случаем цепей являются такие маршруты, которые
не проходят дважды через одну и ту же вершину. Такие маршру-
ты называются простыми цепями. Ясно, что если маршрут
не проходит дважды через одну и ту же вершину, то он не прохо-
дит дважды и через одно и то же
ребро.
Простым циклом называется маршрут, в котором на-
чальная и конечная вершины совпадают, а все остальные верши-
ны различны.
2.1.8. Связность графов
Граф G(V, E) называется связным, если для любой пары
различных вершин этого графа существует цепь, соединяющая
эти вершины. Если для графа G(V, Е) можно указать пару раз-
личных вершин, которые не соединяются цепью (простой цепью),
то граф называется несвязным.
Граф называется k-связным, если его любая пара различных
вершин A и В соединяется
по меньшей мере k простыми цепями,
не имеющими общих вершин, кроме А и В.
2.1.9. Древовидные графы
Различные определения деревьев
Определение 1. Деревом называется конечный связный
граф без циклов.
Из определения 1 следует, что если граф является деревом, то
любая пара его вершин соединяется единственной цепью. Оче-
видно, что это свойство деревьев является не только необходи-
мым, но и достаточным, так как если любая пара вершин графа
73
соединяется единственной цепью, то этот граф связный и не име-
ет циклов. В силу этого можно дать следующее определение.
Определение 2. Деревом называется конечный граф, лю-
бые две вершины которого соединяются единственной цепью.
Определение 3. Деревом называется конечный связный
граф, для которого количество ребер на единицу меньше количе-
ства вершин.
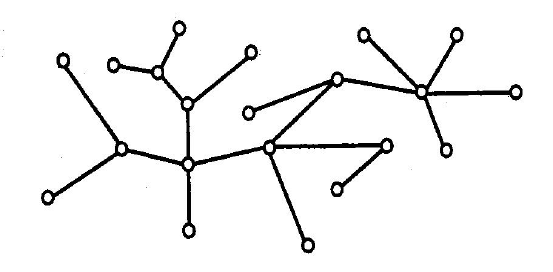
Пример дерева
представлен на рис. 2.8. В качестве несложного
упражнения можно убедиться в корректности еще одного опре-
деления.
Рис. 2.8. Древовидный граф
Определение 4. Деревом называется конечный граф, обла-
дающий свойством: граф не содержит циклов, но добавление
ребра между любыми не смежными вершинами приводит к появ-
лению цикла.
2.1.10. Уникурсальные графы
Задача Эйлера о кенигсбергских мостах
В 1736 г. Эйлером была выполнена работа, в которой содер-
жалось решение знаменитой задачи о кенигсбергских мостах.
Из письма Л. Эйлера от 13 марта 1736 г.: «Мне была предло-
жена задача об острове, расположенном в городе Кенигсберге и
окруженном рекой, через которую перекинуто 7 мостов. Спра-
шивается, может ли кто-нибудь непрерывно обойти их
, проходя
только однажды через каждый мост. И тут же мне было со-
общено, что никто еще до сих пор не смог это проделать, но ни-
кто и не доказал, что это невозможно. Вопрос этот, хотя и ба-
нальный, показался мне достойным внимания тем, что для его
74
решения недостаточны ни геометрия, ни алгебра, ни комбина-
торное искусство. После долгих размышлений я нашел легкое
правило, основанное на вполне убедительном доказательстве,
при помощи которого можно во всех задачах такого рода тот-
час же определить, может ли быть совершен такой обход через
какое угодно число и как угодно расположенных мостов или
не
может».
Идеи Эйлера, использованные им при решении этой задачи,
явились фундаментом теории, впоследствии названной теорией
графов. Суть этой задачи заключается в следующем: можно ли
пройти по всем мостам, изображенным на рис. 2.9, так, чтобы на
каждом из них побывать лишь один раз и вернуться к тому месту,
откуда началась прогулка
?
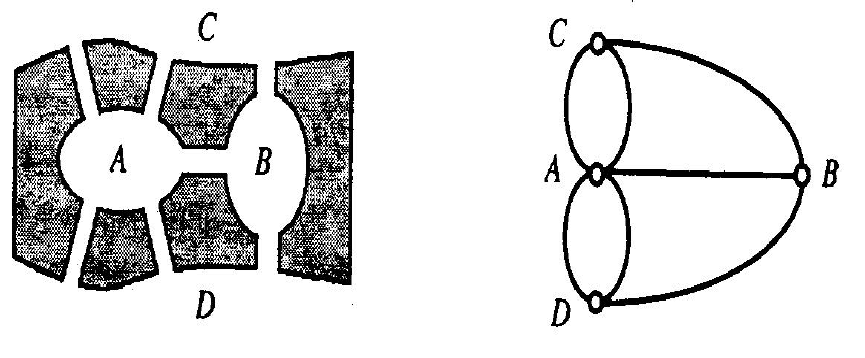
Рис. 2.9. Схема мостов Рис. 2.10. Граф схемы
Ясно, что по условию задачи не имеет значения, как проходит
путь по частям суши A, B, С, D, поэтому их можно изобразить
точками. А так как связи между этими частями суши осуществ-
ляются только через семь мостов, то каждый из мостов можно
изобразить линией, соединяющей соответствующие
вершины. В
результате получается граф, изображенный на рис. 2.10. Если бы
существовал маршрут движения, удовлетворяющий условию за-
дачи, то этот граф было бы возможно нарисовать «одним рос-
черком» (т.е. – без отрыва карандаша от бумаги, проводя по каж-
дому ребру только один раз), начиная и заканчивая рисование в
одной точке
. Эйлером было доказано, что это невозможно. Воз-
никает вопрос: будет ли задача о кенигсбергских мостах иметь
решение, если отказаться от того, чтобы маршрут движения на-
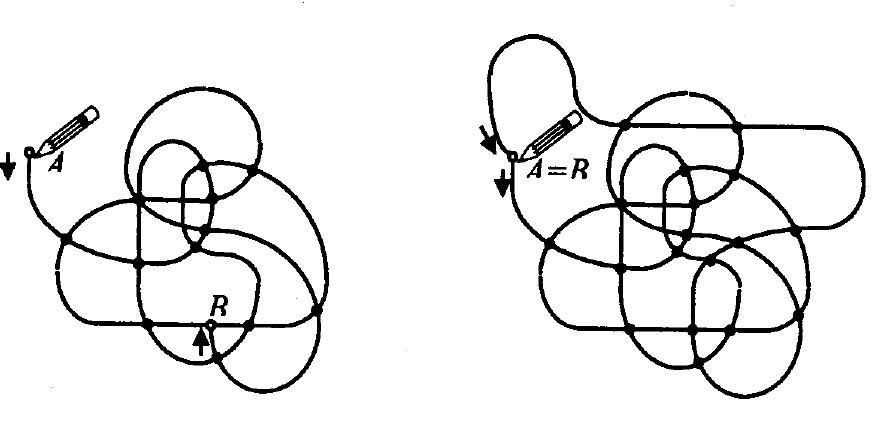
75
чинался и заканчивался в одной точке? В этом случае мы вновь
приходим к задаче об изображении графа одним росчерком. Как
будет показано ниже, граф на рис. 2.10 одним росчерком изобра-
зить невозможно.
Определение уникурсальных графов
Граф называется уникурсальным графом (или эйлеро-
вой линией), если все его ребра можно включить либо в про-
стой цикл, либо в простую цепь. Другими словами, граф называ-
ется уникурсальным, если он рисуется одним росчерком. Если
все ребра графа можно включить в простой цикл, то такой уни-
курсальный граф называется эйлеровым циклом
. Уникур-
сальный граф, не являющийся эйлеровым циклом, называется
эйлеровой цепью. При изображении одним росчерком эйле-
ров цикл начинается и заканчивается в одной точке, а эйлерова
цепь – в различных точках.
Чтобы привести примеры уникурсальных графов, достаточно
на листе бумаги отметить произвольную точку A и, не отрывая
карандаша от бумаги, провести произвольную
самопересекаю-
щуюся кривую так, чтобы она начиналась в этой точке, не имела
отрезков самопересечения и заканчивалась в некоторой точке R
(см. рис. 2.11).
Рис. 2.11. Эйлерова цепь Рис. 2.12. Эйлеров цикл
Ясно, что граф, вершинами которого являются точки самопе-
ресечения кривой вместе с точками A и R, является уникурсаль-
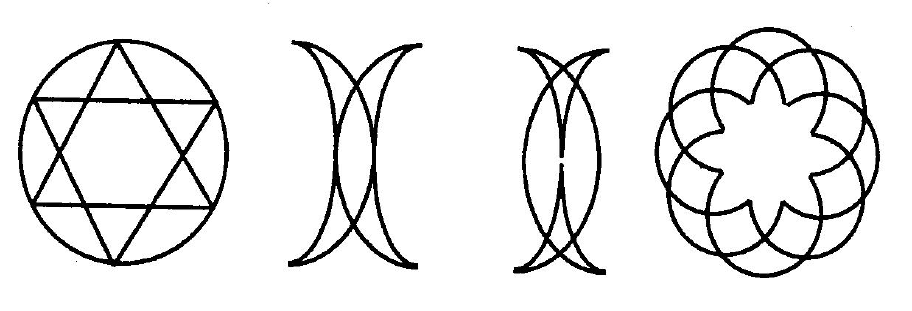
76
ным. При этом если точки A и R совпадают, то мы получим эйле-
ров цикл (см. рис. 2.12), если же точки A и R различны, то мы по-
лучим эйлерову цепь (см. рис. 2.11).
Упражнение. На рис. 2.13 приведено 4 примера эйлеровых
циклов. Попробуйте изобразить эти графы одним росчерком.
Рис. 2.13. Примеры Эйлеровых циклов
Признаки уникурсальных графов
Очевидно, что связность графа является необходимым усло-
вием его уникурсальности. К сожалению, для изображения гра-
фа одним росчерком одной его связности недостаточно. Для то-
го чтобы найти признаки уникурсальности связных графов, по-
наблюдаем за свойствами эйлеровых линий. Если подсчитать
степени всех вершин графов, полученных одним росчерком (см.
рис. 2.11 – 2.13), то можно заметить
, что все эйлеровы циклы
имеют только четные вершины (см. рис. 2.12 и 2.13), а все эйле-
ровы цепи (см. рис. 2.11), имеют ровно две нечетные вершины, а
все их остальные вершины – четны. Приведем без доказательст-
ва несколько теорем.
Лемма. Если связный граф имеет более двух нечетных
вершин, то он не уникурсален. Действительно, если
граф ри-
суется одним росчерком, то его нечетная вершина может
служить либо началом, либо концом пути.
Теорема 1. Связный граф является эйлеровым циклом то-
гда и только тогда, когда он имеет только четные вершины.
При этом начало и конец уникурсального пути совпадают и
могут находиться в любой вершине графа.
77
Теорема 2. Связный граф является эйлеровой цепью тогда
и только тогда, когда он имеет ровно две нечетные вершины,
а остальные вершины этого графа четны. При этом начало и
конец уникурсального пути находятся в нечетных вершинах.
Граф, все вершины которого четны (и, значит, существует эй-
леров цикл), называют эйлеровым графом. Обратившись к
графу в задаче о кенигсбергских мостах, замечаем, что все четыре
его вершины являются нечетными – в каждой из вершин B, С, D
сходятся по три ребра, а в вершине A – пять ребер. Значит, этот
граф не эйлеров. Найти эйлеров цикл (разумеется, после того, как
вы убедились, что заданный граф эйлеров (все вершины четны))
совсем
не трудно: существует универсальный и достаточно про-
стой алгоритм, при помощи которого задача построения эйлерова
цикла всегда разрешима.
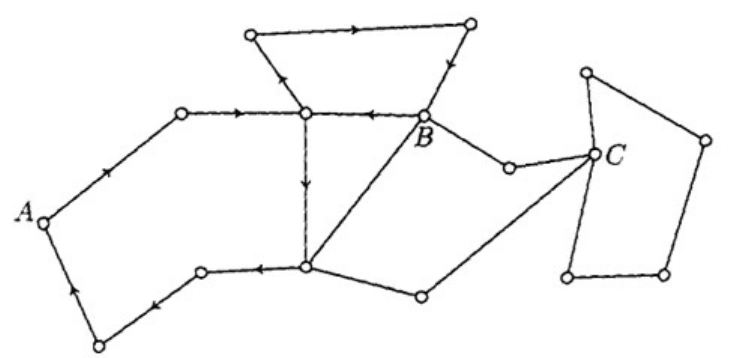
Покажем эффективность этого алгоритма на конкретном при-
мере (см. рис. 2.14).
Пример 1. Выйдя из вершины A и не пытаясь еще раз пройти
по уже пройденному ребру, мы неизбежно вернемся в вершину А.
Это
объясняется тем, что, входя в любую вершину графа (кроме,
быть может, вершины А), мы всегда имеем возможность выйти из
нее (напомним, что в каждой вершине графа сходится четное
число ребер). Следовательно, неутомимо продолжая перемеще-
ние, мы неизбежно вернемся в вершину A, а вернувшись, ока-
жемся перед двумя возможными ситуациями: 1) в построенный
нами цикл входят все ребра графа, 2) остались еще не пройден-
ные ребра.
Рис. 2.14. Эйлеров цикл
78
Первый случай не так интересен: если в построенный цикл
входят все ребра, то поставленная задача решена. Что же касается
второго случая, то здесь в полученном нами цикле (обозначим
его через A) обязательно есть вершина, из которой выходит еще
не пройденное нами ребро. Пусть это вершина В. Об этой верши-
не можно
сказать даже больше: число выходящих из нее ребер,
не принадлежащих построенному циклу A, обязательно четно. И
мы строим новую цепь из вершины B, привлекая только ранее не
пройденные ребра. Ясно, что в результате мы вернемся в верши-
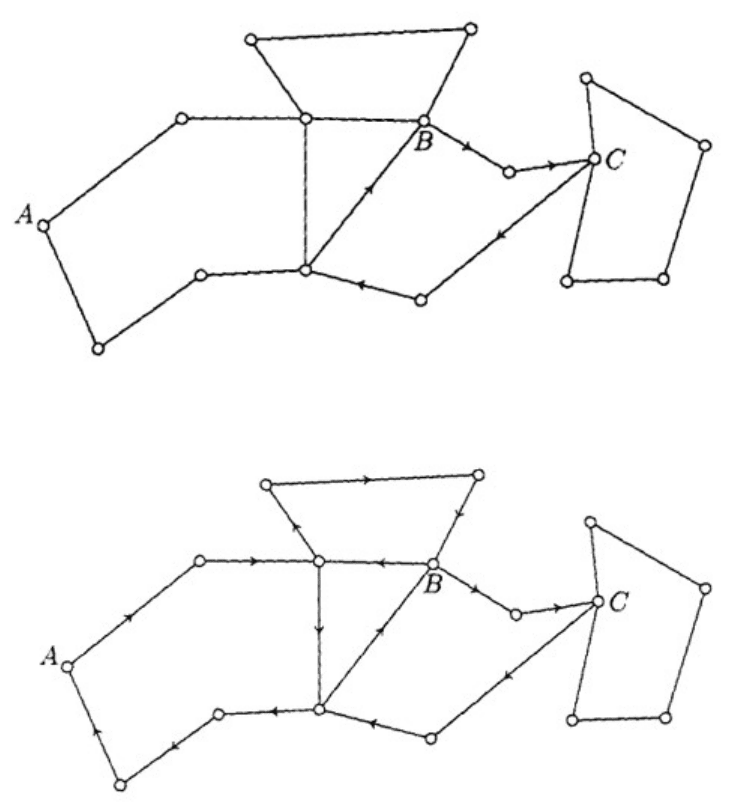
ну B и получится новый цикл – B (рис. 2.15).
Рис. 2.15. Эйлеров цикл
Рис. 2.16. Эйлеров цикл
Теперь легко получить цикл, начинающийся в вершине A и
больший построенного ранее цикла A. Для этого мы сначала пе-
ремещаемся по маршруту A от вершины A до вершины B, затем
79
проходим по циклу B и, вернувшись в вершину В, завершаем пе-
ремещение в вершину А по оставшейся части цикла A (рис. 2.16).
Если мы и на этот раз не прошли по всем ребрам графа, то,
выбрав вершину цикла, построенного по циклам A и B, из кото-
рой исходят ребра, не входящие в
этот цикл, расширяем его опи-
санным выше способом. Повторяя в случае необходимости по-
добные рассуждения достаточное число раз, мы всегда сможем
построить эйлеров цикл за конечное число шагов.
Пример 2. Устроители больших художественных выставок
часто вынуждены решать одну и ту же задачу: как организовать
осмотр, чтобы дать возможность в отведенное время
ознакомить-
ся со всей экспозицией наибольшему числу желающих.
Ясно, что для этого нужно расставить указатели таким обра-
зом, чтобы, перемещаясь в соответствии с предложенными в них
рекомендациями, любой посетитель мог побывать у каждой кар-
тины ровно по одному разу. Если вход и выход совпадают, то
разместить экспонаты следует так, чтобы
схема экспозиции была
эйлеровым графом. Что же касается указателей, то они должны 1)
быть снабжены порядковыми номерами и 2) описывать эйлеров
цикл. Если же вход и выход разные, то схема размещения экспо-
натов должна быть графом, у которого лишь две вершины, соот-
ветствующие входу и выходу, являются нечетными.
Эйлеровы циклы характеризуются тем свойством
, что они
проходят через каждое ребро графа в точности по одному разу.
Аналогичным образом, но только по отношению к вершинам оп-
ределяются для конечных связных графов так называемые га-
мильтоновы циклы: цикл называется гамильтоновым, если
он проходит через каждую вершину графа ровно по одному разу.
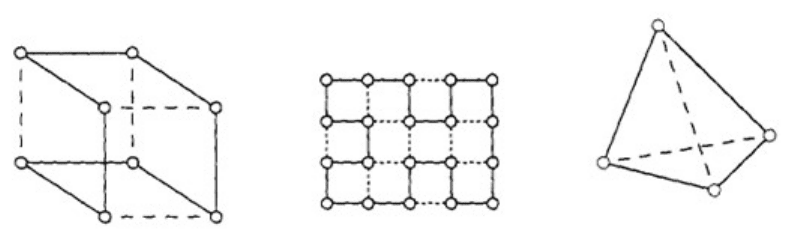
Рис. 2.17. Гамильтоновы циклы
80
На рис. 2.17 приведены гамильтоновы циклы для нескольких
простых графов. Между эйлеровым и гамильтоновым циклами
легко просматривается довольно прозрачная аналогия: первый
проходит ровно один раз по каждому ребру, второй – ровно один
раз через каждую вершину.
На первый взгляд естественно ожидать того, что задача про-
верки, допускает ли данный граф гамильтонов цикл, должна
быть
по сложности сравнима с аналогичной задачей для эйлерова цик-
ла (где достаточно подсчитать четность каждой вершины). Одна-
ко на деле все обстоит значительно сложнее: несмотря на практи-
ческую важность этой проблемы, до сих пор не найдено ни обще-
го критерия, позволяющего устанавливать, является ли заданный
граф гамильтоновым, ни универсального
эффективного алгорит-
ма построения гамильтонова цикла.
Одной из практических задач, связанных с построением га-
мильтонова цикла, является задача о коммивояжере, в которой
нужно найти кратчайший путь, проходящий через заданные
пункты (все расстояния известны) и возвращающийся в исход-
ный пункт.
Так как число пунктов конечно, то в принципе задача может
быть решена
простым перебором.
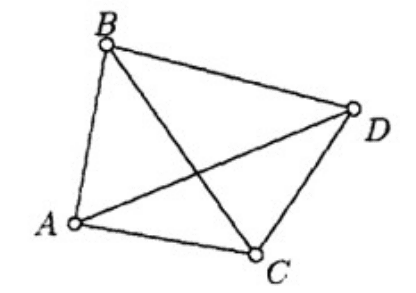
Пример 3. Торговец, живущий в городе A, намерен посетить
города B, С и D, расстояния между которыми ему известны: АВ =
11, АС = 13, AD = 17, BC = 6, BD = 9, CD = 10 (рис. 2.18). Требу-
ется указать кратчайший циклический маршрут из города А, про-
ходящий через три других города.
Рис. 2.18. Граф соединения городов
