Родичев Ю.А. Компьютерные сети - архитектура, технологии, защита
Подождите немного. Документ загружается.

51
в специалистах с высшим и средним специальным образованием
составит до 100 тыс. в год, а к концу срока действия Программы
– более 130 тыс. ежегодно. Мероприятиями Программы преду-
смотрено обеспечить ежегодные объемы подготовки кадров в об-
ласти информационных технологий к 2005 году не менее 25 тыс.
специалистов с высшим образованием и не менее 60 тыс. со
средним специальным и начальным профессиональным образо-
ванием. Дальнейшее развитие кадрового потенциала будет опре-
деляться потребностями рынка рабочей силы этой квалификации.
В рамках реализации данной Программы и программы развития
образования будет достигнут уровень компьютеризации (включая
доступ к Интернету) в 100% для высших учебных заведений к
2005 году и 100% средних учебных заведений к 2010 году.
Создание условий для ускорения процессов внедрения совре-
менных информационных технологий во все сферы обществен-
ной жизни и бизнеса позволит России сократить отставание от
развитых стран мира, избежать информационной и экономиче-
ской изоляции от мировой экономики и мирового сообщества,
обеспечить динамизм процессов международной интеграции.
Решение задач, определенных в Программе, позволит российской
отрасли
связи и информатизации обеспечить жителей всех регио-
нов России широкополосными стационарными и беспроводными
линиями связи. Пользователи персональных компьютеров и мо-
бильных коммуникаторов смогут выходить в Интернет практиче-
ски из любой точки страны. В результате образование и квали-
фицированная медицинская помощь станут доступны населению
по всей территории России, жители страны будут
иметь возмож-
ность приобрести либо реализовать товары по приемлемым це-
нам, найти или предложить на рынке труда свои услуги в любой
точке земного шара. Таким образом, реализация Программы по-
зволит обеспечить эффективность государственного управления
на всей территории России, повысит конкурентоспособность эко-
номики страны за счет снижения издержек и повышения качества
продукции
и услуг, обеспечит рост качества жизни населения.
52
1.6. Основные положения федеральной
целевой программы «Развитие единой
образовательной информационной среды
(2001-2005 годы)»
Программа «Развитие единой образовательной информацион-
ной среды (2001-2005 годы)» утверждена постановлением Прави-
тельства Российской Федерации от 28 августа 2001 г. N 630.
Государственным заказчиком Программы является Министер-
ство образования Российской Федерации. Основные разработчи-
ки Программы – Министерство образования Российской Федера-
ции, Министерство Российской Федерации по связи и информа-
тизации, Министерство экономического развития и торговли
Российской Федерации, Министерство
финансов Российской Фе-
дерации, Министерство промышленности, науки и технологий
Российской Федерации, Министерство юстиции Российской Фе-
дерации.
Цели Программы – создание и развитие в Российской Феде-
рации единой образовательной информационной среды, обеспе-
чивающей:
– единство образовательного пространства на всей территории
страны;
– повышение качества образования во всех регионах России;
– сохранение, развитие и эффективное
использование научно-
педагогического потенциала страны;
– создание условий для поэтапного перехода к новому уровню
образования на основе информационных технологий;
– создание условий для предоставления российских образова-
тельных услуг русскоязычному населению за рубежом.
Задачи Программы:
– формирование информационно-технологической инфра-
структуры системы образования, включая:
– создание федеральной системы информационного и научно-
методического обеспечения
развития образования;
– предоставление образовательным учреждениям средств вы-
числительной техники, средств доступа к глобальным информа-
53
ционным ресурсам, общесистемных и прикладных программных
средств, технического обслуживания;
– применение новых информационных и телекоммуникаци-
онных технологий в учебном процессе, включая:
– создание и использование в учебном процессе современных
электронных учебных материалов наряду с традиционными
учебными материалами;
– разработку электронных средств информационно-
технологической поддержки и развития учебного процесса;
– подготовку педагогических, административных и
инженер-
но-технических кадров образовательных учреждений, способных
эффективно использовать в учебном процессе новейшие инфор-
мационные технологии.
Этапы реализации Программы:
Первый этап – 2001 год. Поставка аппаратно-программного
обеспечения в сельские школы, отбор прикладного программного
обеспечения для использования в сельских школах в переходный
период, организация подготовки учителей сельских школ к рабо-
те с
информационными технологиями в образовании.
Второй этап – 2002-2003 годы. Разработка стратегии и мето-
дологии реализации Программы, организация федеральной сис-
темы информационного и научно-методического обеспечения
развития образования, обеспечение учебных заведений средства-
ми информатизации и доступа к информационно-
образовательным ресурсам, разработка современных электрон-
ных учебных материалов и их экспериментальное апробирова-
ние, разработка программ, учебных
планов и материалов, прове-
дение курсов повышения квалификации и профессиональной пе-
реподготовки педагогических, административных и инженерно-
технических кадров.
Третий этап – 2004-2005 годы. Завершение поставок средств
информатизации в учебные заведения, организация системы тех-
нического обслуживания, разработка и тиражирование электрон-
ных учебных материалов, повышение квалификации и профес-
сиональная переподготовка педагогических, административных и
инженерно-
технических кадров, создание системы открытого об-
разования на основе дистанционных технологий обучения.
54
Основные направления:
1) развитие информационных технологий сферы образования:
– создание основ единой системы информационного и научно-
методического обеспечения образования;
– формирование перечня электронных учебных материалов и
информационно-технологических средств, необходимых для
обеспечения учебного процесса различных уровней образования;
– разработка и тиражирование электронных средств поддерж-
ки и развития учебного процесса;
– организация электронных библиотек
учебных материалов и
обеспечение доступа к ним;
– организация системы открытого образования, включая ин-
терактивные дистанционные технологии обучения учащихся
учебных заведений различного уровня;
– формирование концепции информационной безопасности,
организация и обеспечение соответствующих образовательных
курсов;
– организация сети ресурсных центров;
– разработка нормативных документов по стандартизации в
области образования, открытого образования, включая дистанци-
онные
технологии обучения, информационные технологии, ин-
формационную поддержку образования, телекоммуникационные
сети, открытые системы, системы передачи, хранения и обработ-
ки данных.
2) повышение квалификации и профессиональная переподго-
товка педагогических, административных и инженерно-
технических кадров:
– формирование программ и разработка методического
обеспечения повышения квалификации и профессиональной
переподготовки педагогических, административных и инже-
нерно-технических кадров
в области новых информационных
технологий;
– повышение квалификации и профессиональная переподго-
товка педагогических, административных и инженерно-
технических кадров.
3) оснащение образовательных учреждений средствами ин-
форматизации:
55
– организация конкурсов на лучший проект оснащения обще-
образовательных учреждений средствами информатизации;
– оснащение образовательных учреждений средствами вычис-
лительной техники, средствами телекоммуникаций;
– оснащение образовательных учреждений лицензионными и
сертифицированными программными продуктами, предоставле-
ние услуг по их сопровождению;
– оснащение образовательных учреждений специализирован-
ной мебелью для учебных кабинетов и компьютерных классов.
4) организация системы
технического обслуживания:
– разработка нормативно-технического и методического обес-
печения, организационных форм и принципов управления техни-
ческим обслуживанием на отраслевом, региональном и местном
уровнях;
– создание материально-технической базы и подготовка кад-
ров для центров технического обслуживания.
Ожидаемые результаты:
1) создание основ единой образовательной информационной
среды, обеспечивающей:
– доступ учащихся и преподавателей 50 процентов
общеобра-
зовательных и 70 процентов учебных заведений профессиональ-
ного образования к высококачественным локальным и сетевым
образовательным информационным ресурсам, в том числе к сис-
теме современных электронных учебных материалов по основ-
ным предметам общеобразовательной школы;
– возможность проведения тестирования и оценки качества
образования с использованием специализированного программ-
ного обеспечения на всей территории Российской
Федерации;
– методическую поддержку и возможность непрерывного по-
вышения квалификации преподавателей образовательных учреж-
дений всех уровней;
– подключение вузов к глобальным информационным ресур-
сам по высокоскоростным каналам;
– переход к системе открытого образования на основе инте-
рактивных дистанционных технологий обучения;
– создание для граждан России с ограниченными возможно-
стями условий, обеспечивающих получение
полноценного обра-
56
зования, необходимой специальной (коррекционной) помощи, а
также социальную адаптацию и реабилитацию с помощью обра-
зовательных средств;
– поэтапный переход к новой организации российского обра-
зования на основе информационных технологий.
2) доведение числа компьютеров в общеобразовательных уч-
реждениях до соотношения – 1 компьютер на 80 учащихся;
3) достижение отвечающего современным требованиям уров-
ня подготовки российских преподавателей
в области информаци-
онных технологий;
4) повышение качества обучения в образовательных учрежде-
ниях, находящихся в удалении от методических центров (сельские
школы, школы в закрытых военных городках и др.), путем органи-
зации доступа таких учреждений к существующим образователь-
ным ресурсам, рационального использования педагогических кад-
ров высшей квалификации, подготовки специалистов в области
новых
информационных технологий для этих учреждений;
5) создание сети ресурсных центров, обеспечивающих ин-
формационную и научно-методическую поддержку учебного
процесса, обслуживание аппаратно-программных средств, оказа-
ние консультационных услуг;
6) развитие фундаментальных и прикладных исследований
для реализации задачи, формулой которой является «образование
через всю жизнь».
Полный текст программы помещен на сайте:
WWW. educom. ru/ru/projects/programs/development/
Контрольные вопросы
к главе 1
1. Назовите основные черты информационного общества.
2. Каковы основные задачи по построению информационного
общества?
3. В чем заключается роль образовательных учреждений в по-
строении информационного общества?
4. Назовите основные положения «Окинавской хартии глобаль-
ного информационного общества».
5. Назовите основные цели и этапы реализации ФЦП «Электрон-
ная Россия».
6. Назовите основные цели
и этапы реализации ФЦП «Развитие
единой образовательной информационной среды».
57
ГЛАВА 2
ОСНОВЫ ТЕОРИИ ГРАФОВ
Введение. Происхождение теории графов
Существует большое количество практических задач, рас-
смотрение которых сводится к изучению совокупности объектов,
существенные свойства которых описываются связями между
ними. Например, на карте авиалиний интерес представляет лишь
то, между какими городами имеется связь. При изучении элек-
трических цепей на первый план выступает характер соединений
различных ее элементов. Органические молекулы образуют
структуры
, характерными свойствами которых являются связи
между атомами. В компьютерных сетях важным является харак-
тер связей между узлами. Интерес могут представлять различные
экономические связи, связи и отношения между людьми, собы-
тиями, состояниями, и вообще, между любыми объектами.
В подобных случаях удобно изображать рассматриваемые
объекты точками, называя их вершинами, а связи между
ними
– линиями (произвольной конфигурации), называя их ребрами.
Множество вершин V, связи между которыми определены мно-
жеством ребер Е, называют графом и обозначают G(V, Е).
Допустим, пять государств А, В, С, D, Е, чтобы договориться
о сотрудничестве, послали своих представителей на конферен-
цию. Результатом конференции явилось подписание следующих
договоров: между А и С
, В и С, А и D, D и В, Е и А, В и Е. Дан-
ной ситуации соответствует граф, имеющий пять вершин и шесть
ребер. Примеры геометрической реализации этого графа приве-
дены на рис. 2.1.
Первая работа по графам была выполнена Л. Эйлером в 1736 г.
и посвящалась решению знаменитой задачи о кенигсбергских
мостах. Идеи, предложенные Эйлером в этой работе, легли в
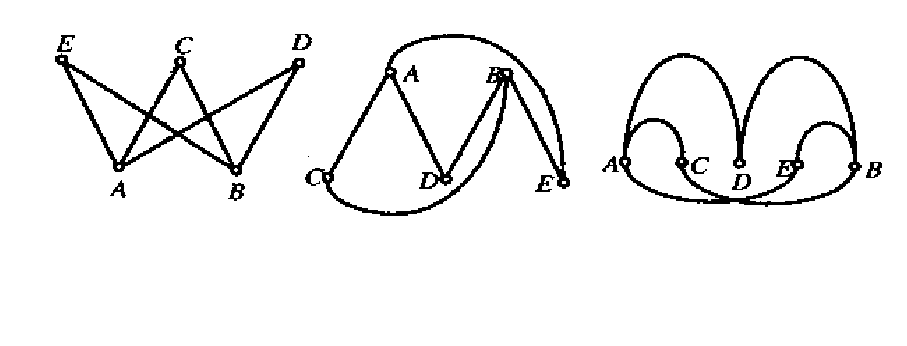
58
основу теории уникурсальных графов. Наряду с решением этой
задачи, Эйлер получил также ряд результатов, которые легли в
основу проблемы планарности графов. В своих работах Эйлер не
использовал термин «граф». Впервые этот термин в 1936 г. ввел
Д. Кёниг, назвав графами схемы, состоящие из множества точек и
связывающих эти точки отрезков прямых и
кривых линий. Тео-
рия графов связана с именами многих известных математиков. До
конца XIX в. графы применялись лишь при решении некоторых
занимательных задач. Однако в начале ХХ в. теория графов
оформилась в виде самостоятельной математической дисципли-
ны. Наряду с многочисленными головоломками и играми на гра-
фах появились важные практические приложения графов,
многие
из которых требовали тонких математических методов. Так,
Кирхгоф применил графы для анализа электрических цепей.
В настоящее время теория графов широко применяется в раз-
личных областях науки и техники. К числу прикладных задач,
решаемых при помощи графов, относятся, например, анализ и
синтез цепей и систем, проектирование каналов связи и исследо-
вание
процессов передачи информации, построение контактных
схем и исследование конечных автоматов, сетевое планирование
и управление, исследование математических операций, выбор оп-
тимальных потоков в сетях, моделирование нервной системы жи-
вых организмов, исследование случайных процессов и многие
другие задачи. Теория графов тесно связана с геометрией и топо-
логией, теорией множеств и математической логикой,
теорией
вероятностей и математической статистикой, теорией матриц и
другими разделами математики.
Рис. 2.1. Геометрическая реализация графа
59
2.1. Неориентированные графы
2.1.1. Абстрактное определение графа
Строгое абстрактное определение графа можно дать в терми-
нах теории множеств. Пусть Х – произвольное непустое множе-
ство и X×X – его декартов квадрат, т.е. множество всех упо-
рядоченных пар (x
1
, х
2
) из элементов множества Х. Если множе-
ство Х – конечно и состоит из n элементов, то его декартов квад-
рат X×X содержит n
2
пар, и пары (x
1
, х
2
) и (х
2
, x
1
) являются раз-
личными элементами множества X×X при x
1
≠х
2
. Иногда множест-
во X×X называют упорядоченным произведением множества Х на
себя.
Рассмотрим теперь так называемое неупорядоченное произве-
дение Х&Х множества Х на себя, которое определяется как мно-
жество всех неупорядоченных пар из элементов множества X.
Элементы из X&X будем обозначать (x
1
&х
2
). Ясно, что во множе-
стве X&X пары (x
1
&х
2
) и (х
2
&x
1
) не различимы. Если множество X
– конечно и состоит из n элементов, то множество X&X содержит
n(n+1)/2 элементов.
Графом G(V, Е, f) называется совокупность непустого мно-
жества V, изолированного от него произвольного множества Е и
отображения f: Е
→
V&V множества Е в V&V, которое каждому
элементу из Е ставит в соответствие некоторый элемент из V&V.
При этом множества V и Е называются соответственно множе-
ством вершин и множеством ребер графа G(V, Е, f), а
отображение f называется отображением инциденции
этого графа. Граф называется конечным, если множества V и Е
содержат
конечное число элементов.
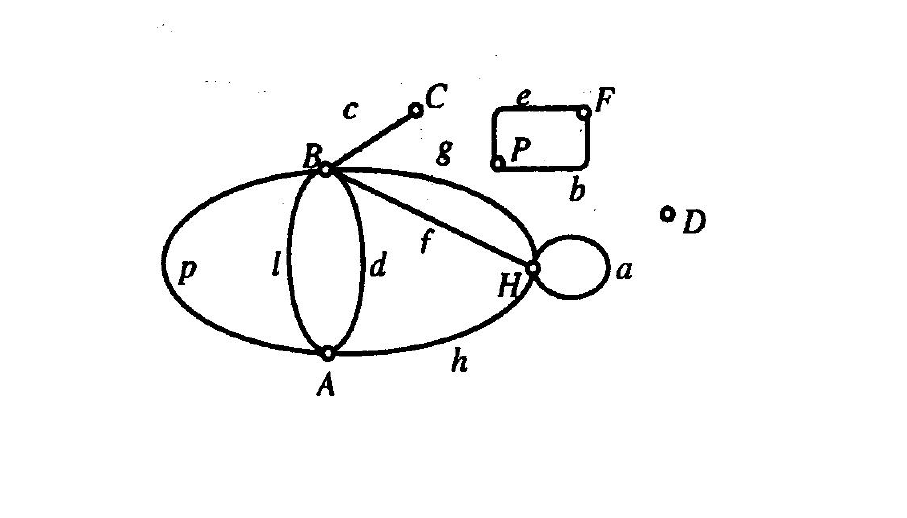
Рассмотрим пример. Пусть множество V состоит из 7 точек,
V={A,В,C,D,F,Н,P}, а множество Е – из 10 линий
E={a,b,с,d,e,f,g,h,p,l} (см. рис. 2.2).
Тогда отображение f: Е→V&V, определяемое по закону
f: a→(H&H), b→(P&F), c→(B&C), d→(A&B), e→(P&F),
f→(B&H), g→(B&H), h→(A&H), p→(A&B), l→(A&B)
является отображением инциденции для графа G(V, Е, f). Этот
граф имеет 7 вершин
и 10 ребер.
60
В некоторых случаях, если отображение инциденции явно не
задано, для графа G(V, Е, f) будем использовать обозначение G(V,
Е). В случаях, когда множества вершин и ребер известны из кон-
текста задачи, граф G(V, Е, f) будем обозначать через G. Заметим,
что часто вершины и ребра графа объединяются одним общим
термином – элементы графа.
На первый взгляд может показаться, что данное абстрактное
определение графа является сложным и граф достаточно мыслить
как совокупность точек и кривых, соединяющих некоторые из
этих точек. Но на самом деле это не так. Определение абстракт-
ного графа позволяет избавиться от случайных характеристик его
геометрических моделей и сохранить все существенные свойства
графа
. Кроме того, абстрактное определение позволяет расши-
рить область применения теории графов, так как очень многие
реальные объекты можно рассматривать как элементы некоторо-
го графа.
2.1.2. Определение геометрического графа
Для определения геометрического графа напомним два важ-
ных понятия из евклидовой геометрии. Пусть U – трехмерное
евклидово пространство или двумерная евклидова плоскость.
Простой незамкнутой кривой в U называется непре-
рывная самонепересекающаяся кривая, соединяющая две различ-
Рис. 2.2. Представление множеств графом
