Richards J.A., Jia X. Remote Sensing Digital Image Analysis: An Introduction

Подождите немного. Документ загружается.

7.6 Sampling Theory 173

7.5.3

The Convolution Theorem

This theorem is readily veriﬁed using the deﬁnition of convolution and the deﬁnition

of the Fourier transform. It has two forms (Papoulis, 1980). These are:

y(t) = f

(t) ∗ f

(t)

then

Y(ω) = F

(ω)F

(ω), (7.10a)

and, if

Y(ω) = F

(ω) ∗ F

(ω)

then

y(t) =

2π

(t)f

(t) (7.10b)

7.6

Sampling Theory

The previous sections have dealt with functions that are continuous with time (or

with position, as the case may be). However our interest principally is in functions,

and images, that are discrete with time or position. Discrete time functions and digital

images can be considered to be the result of the corresponding continuous functions

having been sampled on a regular basis. Again, we will develop the concepts of

sampling using functions of a single variable, such as time; the concepts are readily

extended to two dimensional image functions.

A periodic sequence of impulses, spaced T apart,

(t) =

∞



k=−∞

δ(t − kT ) (7.11)

can be considered as a sampling function, i.e. it can be used to extract a uniform set

of samples from a function f(t)by forming the product

f = f (t)(t). (7.12)

According to (7.5a), f is a sequence of samples of value f(kT)δ(t −kT ). Despite

the undeﬁned magnitude of the delta function we will be content in this treatment to

regard that product as a sample of the function f(t). Strictly this should be interpreted

in terms of so-called distribution theory; a simple interpretation of (7.12) as a set

of uniformly spaced samples of f(t)however will not compromise our subsequent

development.

174 7 Fourier Transformation of Image Data

It is important to consider the Fourier transform of the set of samples in (7.12)

so that the frequency composition of a sampled function can be appreciated. This

can be done using the convolution theorem (7.10b) provided the Fourier transform

of (t) can be found.

The Fourier transform of (t) can be determined via its Fourier series. From (7.7b)

and (7.5b) the Fourier series coefﬁcients of (t) are given by



T/2



−T/2

δ(t) e

−jnω

dt =

which, with the expression for the Fourier transform of a periodic function in Sect. 7.4,

gives the Fourier transform of (t) as

(ω) =

2π

∞



n=−∞

δ(ω − nω

) (7.13)

where ω

= 2π/T . Thus the Fourier transform of the periodic sequence of impulses

spaced T apart in time is itself a periodic sequence of impulses in the frequency

domain, spaced 2π/T rad s

−1

apart (or 1/T Hz apart). Thus if f(t)has the spectrum

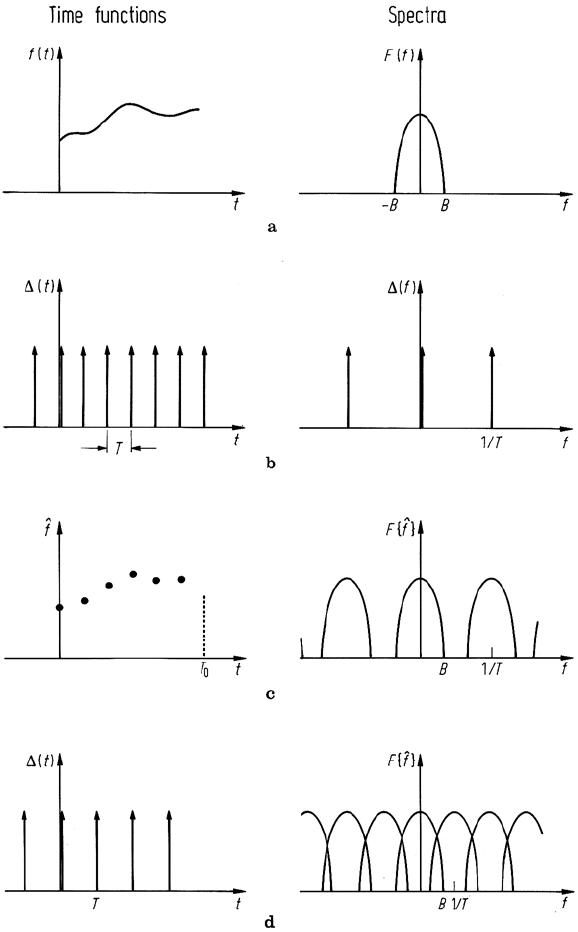
F(ω) (i.e. Fourier Transform) depicted in Fig. 7.6a then the spectrum of the set of

samples in (7.12) is as shown in Fig. 7.6c. This is given by convolving F(ω)with the

sequence of impulses in (7.13), according to (7.10b). Recall that convolution with

an impulse shifts a function to a new origin centred on the impulse.

Figure 7.6c demonstrates that the spectrum of a sampled function is a periodic

repetition of the spectrum of the unsampled function, with the repetition period in

the frequency domain determined by the rate at which the time function is sampled.

If the sampling rate is high then the segments of the spectrum are well separated. If

the sampling rate is low then the segments in the spectrum are close together.

In the illustration shown in Fig. 7.6 the spectrum of f(t)is shown to be limited

to frequencies below B Hz. (2πB rad · s

−1

); B is referred to as the bandwidth of

f(t). Not all real non-periodic functions have a limited bandwidth – the single pulse

of Fig. 7.4 is an example of this – however it suits our purpose here to assume there

is a limit to the frequency composition of functions of interest to us, deﬁned by the

signal bandwidth.

If adjacent segements are to remain separated as depicted in Fig. 7.6c then it is

clear that

> 2B (7.14)

i.e. that the rate at which the function f(t)is sampled must exceed twice the band-

width of f(t). Should this not be the case then the segments of the spectrum of the

sampled function overlap as shown in Fig. 7.6d, causing a form of distortion called

aliasing.

A sampling rate of 2 B in (7.14) is referred to as the Nyquist rate; Eq. (7.14) itself

is often referred to as the sampling theorem.

7.6 Sampling Theory 175

Fig. 7.6. Development of the Fourier transform of a sampled function. a Unsampled function

and its spectrum; b Periodic sequence of impulses and its spectrum; c Sampled function and

its spectrum; d Sub-Nyquist rate sampling impulses and spectrum with aliasing. F represents

Fourier transformation

176 7 Fourier Transformation of Image Data

7.7

The Discrete Fourier Transform

7.7.1

The Discrete Spectrum

Consider now the problem of ﬁnding the spectrum (i.e. of computing the Fourier

transform) of a sequence of samples. This is the ﬁrst stage in our computation of

the Fourier transform of an image. Indeed, the sequence of samples to be considered

here could be looked at as a single line of pixels in digital image data.

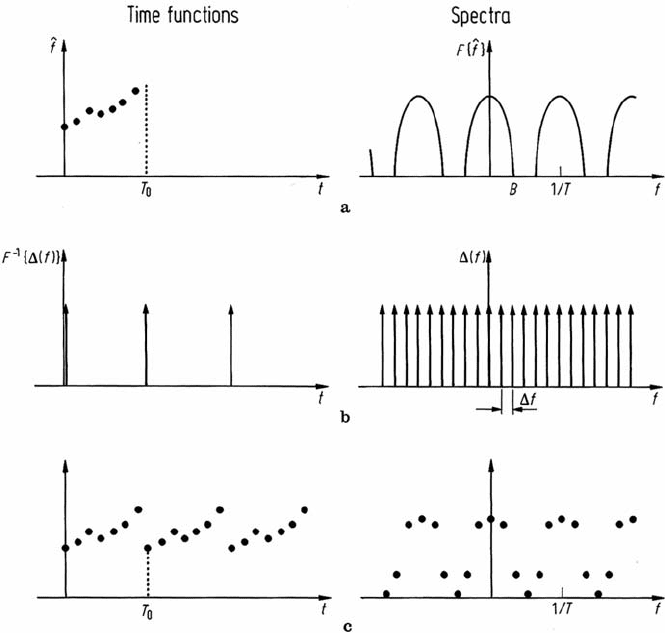
Figure 7.7a shows that the spectrum of a set of samples is itself a continuous

function of frequency. For digital processing clearly it is necessary that the spectrum

be also represented by a set of samples, that would, for example, exist in computer

Fig. 7.7. Effect of sampling the spectrum. a Sampled function and its spectrum; b Periodic

sequence of impulses used to sample the spectrum (right) and its time domain equivalent (left);

c Sampled version of the spectrum (right) and its time domain equivalent (left); the latter is a

periodic version of the samples in a. In these F

−1

represents an inverse Fourier transformation

7.7 The Discrete Fourier Transform 177

memory. Therefore we have to introduce a suitable sampling function also in the

frequency domain. For this purpose consider an inﬁnite periodic sequence of impulses

in the frequency domain spaced f (i.e. ω/2π ) apart as shown in Fig. 7.7b. It

can be shown that the inverse transform of this sequence is another sequence of

impulses in the time domain, spaced T

= 1/f apart. This can be appreciated

readily from (7.11) and (7.13), although here we are going from the frequency domain

to the time domain rather than vice versa.

If the (periodic) spectrum F(ω)in Fig. 7.7a is multiplied by the frequency domain

sampling function of Fig. 7.7b then the convolution theorem (7.10a) implies that the

samples of f(t)will be formed into a periodic sequence with period T

as illustrated

in Fig. 7.7c. It is convenient if the number of samples used to represent the spectrum is

the same as the actual number of samples taken of f(t). Let this number be K. (There

is a distortion introduced by using a ﬁnite rather than inﬁnite number of samples.

This will be addressed later.) Since the time domain has samples spaced T apart, the

duration of sampling is KT seconds. It is pointless sampling the time domain over

a period longer than T

since no new information is added. Simply other periods

are added. Consequently the optimum sampling time is T

, so that T

= KT . Thus

the sampling increment in the frequency domain is f = 1/T

= 1/KT .Itisthe

inverse of the sampling duration. Likewise the total unambiguous bandwidth in the

frequency domain is K × f = 1/T, covering just one segment of the spectrum.

With those parameters established we can now consider how the Fourier transform

operation can be modiﬁed to handle digital data.

7.7.2

Discrete Fourier Transform Formulae

Let the sequence φ(k),k = 0,...K − 1 be the set of K samples taken of f(t)over

the sampling period 0 to T

. The samples correspond to times t

= kT .

Let the sequence F(r),r = 0,...K − 1 be the set of samples of the frequency

spectrum. These can be derived from the φ(k) by suitably modifying (7.8a). For

example, the integral over time can be replaced by the sum over k = 0toK −1, with

dt replaced by T , the sampling increment. The continuous function f(t)is replaced

by the samples φ(k) and ω = 2πf is replaced by 2πrf, with r = 0,...K − 1.

Thus ω = 2πr/T

. The time variable t is replaced by kT = kT

/K, k = 0,...K−1.

With these changes (7.8a) can be written in sampled form as

F(r) = T

K−1



k=0

φ(k)W

,r = 0,...K − 1 (7.15)

with

W = e

−j2π/K

. (7.16)

Equation (7.15) is known as the discrete Fourier transform (DFT). In a similar manner

a discrete inverse Fourier transform (DIFT) can be derived that allows reconstruction

178 7 Fourier Transformation of Image Data

of the time sequence φ(k) from the frequency samples F(r). This is

φ(k) =

K−1



r=0

F(r)W

−rk

,k = 0,...K − 1 (7.17)

Substitution of (7.15) into (7.17) shows that those two expressions form a Fourier

transform pair. This is achieved by putting k = l in (7.17) so that

φ(l)=

K−1



r=0

F(r)W

−rl

K−1



r=0

K−1



k=0

φ(k)W

r(k−l)

K−1



k=0

φ(k)

K−1



r=0

r(k−l)

The second sum in this expression is zero for k = l; when k = l it is K, so that

the right hand side of the equality then becomes φ(l) as required. An interesting

aspect of this development has been that T has cancelled out, leaving 1/K as the

net constant from the forward and inverse transforms. As a result (7.15) and (7.17)

could conveniently be written

F(r) =

K−1



k=0

φ(k)W

,r = 0,...K − 1 (7.15



)

φ(k) =

K−1



r=0

F(r)W

−rk

,k = 0,...K − 1(7.17



)

7.7.3

Properties of the Discrete Fourier Transform

Three properties of the discrete Fourier transform and its inverse are of importance

here.

Linearity: Both the DFT and DIFT are linear operations. Thus if F

(r) is the DFT

of φ

(k) and F

(r) is the DFT of φ

(k) then for any complex constants a and b,

(r) + bF

(r) is the DFT of aφ

(k) + bφ

(k).

Periodicity: From (7.16), W

= 1 and W

= 1 for k integral. Thus for r



= r +K

F(r



) = T

K−1



k=0

φ(k) W

(r+K)k

= F(r).

7.7 The Discrete Fourier Transform 179

Therefore in general

F(r + mK) = F(r) (7.18a)

φ(k + mK) = φ(k) (7.18b)

where m is an integer. Thus both the sequence of time samples and the sequence

of frequency samples are periodic with period K. This is consistent with the de-

velopment of Sect. 7.7.1 and has two important implications. First, to generate the

Fourier series components of a periodic function, samples need only be taken over

one period. Secondly, sampling converts an aperiodic sequence into a periodic one,

the period being determined by the sampling duration.

Symmetry: Let r



= K − r in (7.15), to give F(r



) = T

K−1



k=0

φ(k)W

−rk

Since W

= 1 this shows F(K − r) = F(r)

∗

where here ∗ represents complex

conjugate. This implies that the amplitude spectrum is symmetric about K/2 and the

phase spectrum is antisymmetric (i.e. odd).

7.7.4

Computation of the Discrete Fourier Transform

It is convenient to consider the reduced form of (7.15):

A(r) =

F(r) =

K−1



k=0

φ(k)W

,r = 0,...K − 1 (7.19)

Computation of the K values of A(r) from the K samples φ(k)requires K

multipli-

cations and K

additions, assuming that the required values of W

would have been

calculated beforehand and stored. Since the W

are complex, the multiplications

and additions necessary to evaluate A(r) are complex. Thus, as the number of sam-

ples φ(k) becomes large, the time required to compute the sampled spectrum A(r)

increases enormously (as the square of the number of samples). Between 1000 and

10,000 samples may in fact require unacceptably high computing time. A technique

is required therefore to reduce substantially the number of arithmetic operations

required in computing discrete Fourier transforms.

7.7.5

Development of the Fast Fourier Transform Algorithm

Assume K is even; in fact the algorithm to follow will require K to be expressible

as K = 2

where m is an integer. From φ(k) form two sequences Y(k) and Z(k)

each of K/2 samples. The ﬁrst contains the even numbered samples of φ(k) and the

second the odd numbered samples, viz.

Y(k) : φ(0), φ(2),...φ(K − 2)

Z(k) : φ(1), φ(3),...φ(K − 1)

180 7 Fourier Transformation of Image Data

so that

Y(k) = φ(2k)

Z(k) = φ(2k + 1)

k = 0,...

− 1.

Equation (7.19) can then be written

A(r) =

K/2−1



k=0

{Y(k)W

2rk

+ Z(k) W

r(2k+1)

}

K/2−1



k=0

Y(k)W

2rk

+ W

K/2−1



k=0

Z(k) W

2rk

=B(r) + W

C(r)

where B(r) and C(r) will be recognised as the discrete Fourier transforms of the

sequences Y(k)and Z(k). These are periodic, with period K/2, according to (7.18).

Since W

K/2

=−1 it can be shown that the ﬁrst K/2 samples of A(r) and the last

K/2 samples of A(r) can be obtained from the same amount of computation, viz;

A(r) = B(r) + W

C(r)



r +



= B(r) − W

C(r)



r = 0,...

− 1 (7.20)

Furthermore values of W

only up to W

K/2

are required.

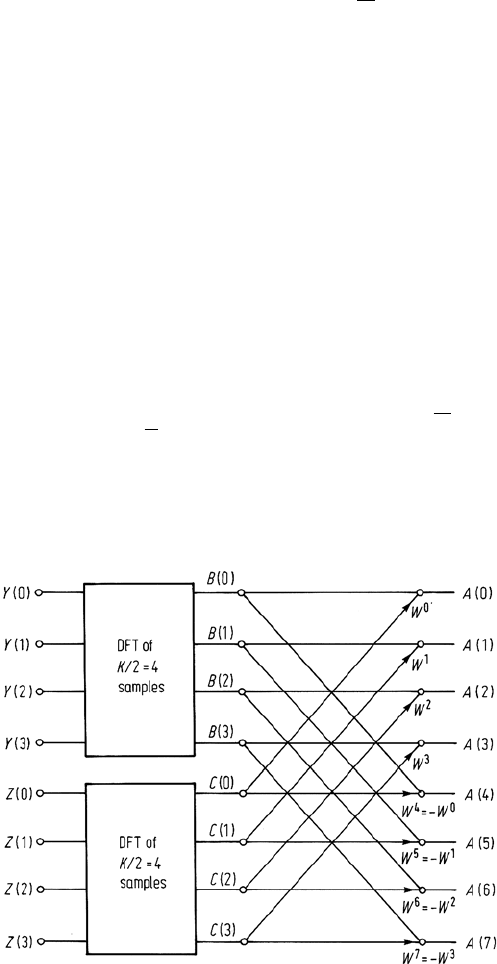
The procedure of (7.20) can be represented conveniently in ﬂow chart form. This

is shown for K = 8 in Fig. 7.8

Fig. 7.8. Flow chart for the ﬁrst stage in the development of the fast Fourier transform algo-

rithm, for the case of K = 8

7.7 The Discrete Fourier Transform 181

Equation (7.20) requires the Fourier transforms B(r) and C(r). The same pro-

cedure can again be used to advantage for these; Y(k) and Z(k) are each broken

up into sequences of odd and even samples, requiring Y(k) and Z(k) to contain an

even number each. This in turn means that K had to be divisible at least by 4. Let

S(k) contain the even numbered samples of Y(k) and T(k)the odd numbered sam-

ples. Also let U(k) contain the even numbered samples of Z(k) and V(k) the odd

numbered samples:

S(k) : Y(0), Y (2), ... (i.e. φ(0), φ(4), ...)

T(k): Y(1), Y (3), ... (i.e. φ(2), φ(6), ...)

U(k) : Z(0), Z(2), ... (i.e. φ(1), φ(5), ...)

V(k): Z(1), Z(3), ... (i.e. φ(3), φ(7), ...)

If the discrete Fourier transforms of these are denoted D(r), E(r), G(r) and H(r)

respectively, each containing K/4 points, then

B(r)=

K/2−1



k=0

Y(k)W

2rk

=D(r) + W

E(r)

which can be written

B(r) = D(r) + W

E(r)



r +



= D(r) − W

E(r)

⎤

⎥

⎦

r = 0,...

− 1

again showing that the ﬁrst and second halves of the set of B(r) can be obtained by

the same calculations. Similarly

C(r) = G(r) + W

H(r)



r +



= G(r) − W

H(r)

⎤

⎥

⎦

r = 0,...

− 1.

Figure 7.9 shows how the ﬂow chart of Fig. 7.8 can be modiﬁed to take account of

this development.

Clearly the procedure followed to this point can be repeated as many times as

there are discrete Fourier transforms left to compute. Ultimately transforms will

be required on sequences with just two samples each. For example if K = 8, the

sequences S, T , U and V will each contain only two samples and their discrete

Fourier transforms will be of the form

D(r)=



k=0

S(k) W

4rk

,r= 0, 1

=S(0)W

+ S(1)W

r = 0, 1

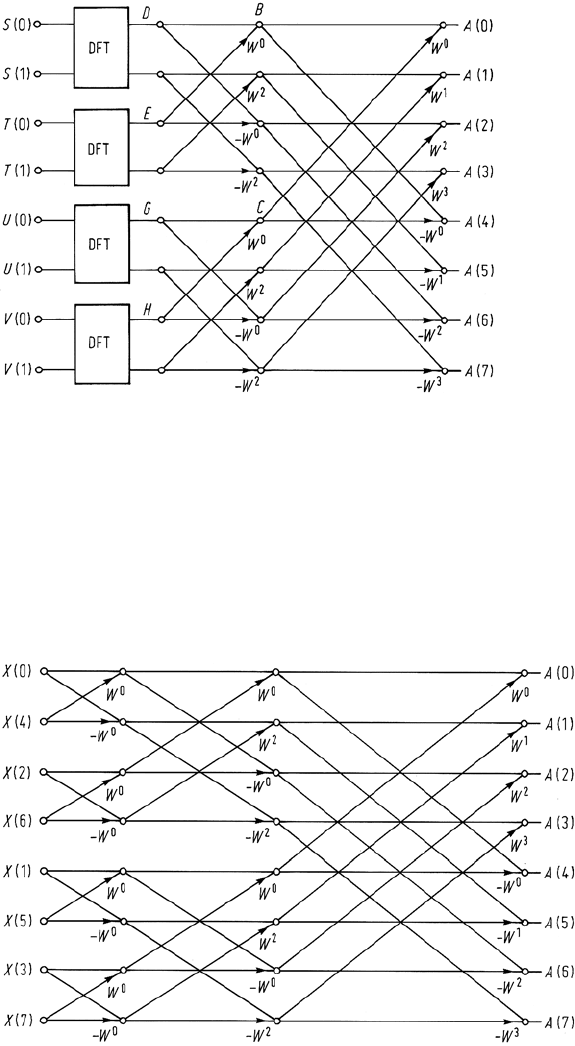
182 7 Fourier Transformation of Image Data

Fig. 7.9. Flow chart for the second stage of the development of the fast Fourier transform

algorithm, for the case of K = 8

i.e. D(0) =S(0) + S(1)

D(1) =S(0) − S(1),

showing that the discrete Fourier transform of two samples is obtained by simple

addition and subtraction. Doing likewise for the other sequences gives the ﬁnal ﬂow

chart for K = 8 as shown in Fig. 7.10.

Fig. 7.10. Flow chart for a complete fast Fourier transform evaluation when K = 8