Richards J.A., Jia X. Remote Sensing Digital Image Analysis: An Introduction
Подождите немного. Документ загружается.

162 6 Multispectral Transformations of Image Data
R.J. Kauth and G.S. Thomas, 1976: The Tasseled Cap – A Graphic Description of the Spectral-
Temporal Development ofAgricultural Crops as Seen by Landsat. Proc. LARS 1976 Symp.
on Machine Process. Remotely Sensed Data, Purdue University.
S.I. Olsen, 1993: Estimation of Noise in Images: an Evaluation. Graphical Models and Image
Processing, 55, 319–323.
J.A. Richards, 1984: Thematic Mapping from Multitemporal Image Data Using the Principal
Components Transformation. Remote Sensing of Environment, 16, 35–46.
A. Santisteban and L. Muñoz, 1978: Principal Components of a Multispectral Image: Appli-
cation to a Geologic Problem. IBM J. Research and Development, 22, 444–454.
J.M. Soha and A.A. Schwartz, 1978: Multispectral Histogram Normalization Contrast En-
hancement. Proc. 5th Canadian Symp. on Remote Sensing, 86–93.
P.H. Swain and S.M. Davis (Eds.), 1978: Remote Sensing: The Quantitative Approach, New
York, McGraw-Hill.
M.M. Taylor, 1973: Principal Components Colour Display of ERTS Imagery. Third Earth
Resources Technology Satellite-1 Symposium, NASA SP-351, 1877–1897.
Problems
6.1 (a) At a conference research group A and research group B both presented papers on
the value of the principal components transformation (also known as the Karhunen-Loève or
Hotelling transform) for reducing the number of features required to represent image data.
Group A described very good results that they had obtained with the method whereas Group
B indicated that they felt it was of little use. Both groups were using image data with only two
spectral components. The covariance matrices for their respective images are:
Σ
A
=
5.44.5
4.56.1
Σ
B
28.04.2
4.216.4
Explain the points of view of both groups.
(b) If information content can be related directly to variance indicate how much information
is discarded if only the first principal component is retained by both groups.
6.2 Suppose you have been asked to describe the principal components transformation to a
non-specialist. Write a single paragraph summary of its essential features, using diagrams if
you wish, but no mathematics.
6.3 (For those mathematically inclined), Demonstrate that the principal components transfor-
mation matrix developed in Sect. 6.1.2 is orthogonal.
6.4 Colour image products formed from principal components generally appear richer in
colour than a colour composite product formed by combining the original bands of remote
sensing image data. Why do you think that is so?
6.5 (a) The steps involved in computing principal component images may be summarised as:
calculation of the image covariance matrix
eigenanalysis of the covariance matrix
computation of the principal components.
Assessments can be made in the first two steps as to the likely value in proceeding to compute
the components. Describe what you would look for in each case.
(b) The covariance matrix need not be computed over the full image to produce a principal

Problems 163
components transformation. Discuss the value of using training areas to define the portion of
image data to be taken into account in compiling the covariance matrix.
6.6 Imagine you have two images from a sensor which has a single band in the range 0.9 to
1.1 µm. One image was taken before a flood occurred. The second shows the extent of flood
inundation. Produce a sketch of what the “two-date” multispectral space would look like if the
image from the first date contained rich vegetation, sand and water and that in the second date
contains the same cover types but with an expanded region of water. Demonstrate how a two
dimensional principal components transform can be used to highlight the extent of flooding.
6.7 Describe the nature of the correlations between the pairs of axis variables (e.g. bands) in
each of the cases in Fig. 6.14.
Fig. 6.14. Examples of two dimensional correlations
6.8 The covariance matrix for an image recorded by a particular four channel sensor is as
shown below. Which band would you discard if you had to construct a colour composite
display of the image by assigning the remaining three bands to each of the colour primaries?
Σ =
⎡
⎢
⎢
⎢
⎢
⎣
35 10 10 5
10 20 12 2
10 12 40 30
5 2 30 30
⎤
⎥
⎥
⎥
⎥
⎦
7
Fourier Transformation of Image Data
7.1
Introduction
Many of the geometric enhancement techniques used with remote sensing image
data can be carried out using the simple template-based techniques of Chap. 5. More
flexibility is offered however if procedures are implemented in the so-called spatial
frequency domain by means of the Fourier transformation. As a simple illustration,
filters can be designed to extract periodic noise from an image that is unable to be
removed by practical templates. As demonstrated in Sect. 5.4 the computational cost
of using Fourier transformation for geometric operations is high by comparison to
the template methods usually employed. However with the computational capacity
of modern workstations, and the flexibility available in Fourier transform processing,
this approach is one that should not be ignored.
Development of Fourier transform theory depends upon a knowledge of complex
numbers and facility with integral calculus. The reader without that background may
wish to pass over this Chapter and may do so without detracting from material in the
remainder of the book. It is the purpose of the Chapter to present an overview of the
significant aspects of the theory of Fourier transformation of image data. In its entirety
the topic is an extensive one and well beyond the scope of this treatment. Instead the
material presented in the following will serve to introduce the operational aspects of
the topic, with little dependence on proofs and theory. Should the treatment be found
to be too brief, particularly in the background material of Sects. 7.2 to 7.5, more
details can be found in Brigham (1974, 1988), and McGillem and Cooper (1984).
Another transformation that now finds wide application to images is that based
on the definition of wavelets (Castleman, 1996).
7.2
Special Functions
A number of mathematical functions are important in both developing and under-
standing the Fourier transformation. These are reviewed in this section along with
some properties that will be of use later on.

166 7 Fourier Transformation of Image Data
Although functions of interest in image processing have position as their inde-
pendent variable, it will be convenient here to use functions of time. These will be
interpreted as functions of position as required.
7.2.1
The Complex Exponential Function
The complex exponential is defined by
f(t) = Re
jωt
(7.1a)
where j =
√
−1, R is the amplitude of the function and ω is called its radian
frequency. The units of ω are radians per second (or radians per unit of spatial
variable). Frequently ω is expressed in terms of “natural” frequency
f = ω/2π (7.1b)
where f has units of hertz (or cycles per spatial variable). The complex exponential
is periodic, with period T = 2π/ω. This is appreciated by plotting it as a function
of the independent variable on the complex (argand) plane. Alternatively, we can
express
f(t) = Re
±jωt
= R cos ωt ± j R sin ωt (7.1c)
to see its periodic behaviour in terms of sinusoids. For convenience we will now
choose R = 1. From this last expression we see
cos ωt = Re{e
jωt
}
sin ωt = Jm{e
jωt
}
where Re and Jm are operators that select the real and imaginary parts of a complex
number.
Finally, it can be seen from (7.1c)
cos ωt =
1
2
(e
jωt
+ e
−jωt
) (7.2a)
sin ωt =
1
2j
(e
jωt
− e
−jωt
) (7.2b)
7.2.2
The Dirac Delta Function
A function of particular importance in determining properties of sampled signals,
which include digital image data, is the impulse function, also referred to as the Dirac
delta function. This is a spike-like function of infinite amplitude and infinitessimal
duration. It cannot be defined explicitly. Instead it is defined by a limiting operation
as in the following manner.
Consider the rectangular pulse of duration α and amplitude 1/α as seen in Fig. 7.1.
Note that the area under the curve is 1. Accordingly the delta function δ(t) is defined
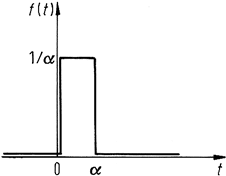
7.2 Special Functions 167
Fig. 7.1. Pulse which approaches an impulse in the limit
as α → 0
as the pulse in the limit as α goes to zero. As a formal definition, the best that can be
done is
δ(t) = 0 for t = 0 (7.3a)
and
∞
−∞
δ(t)dt = 1 (7.3b)
This turns out to be sufficient for our purposes. Equation (7.3a) defines a delta function
at the origin; an impulse at time t
0
is defined by
δ(t − t
0
) = 0 for t = t
0
(7.4a)
and
∞
−∞
δ(t − t
0
)dt = 1 (7.4b)
7.2.2.1
Properties of the Delta Function
From the definition of the delta function it can be seen that the product of a delta
function with another function is
δ(t − t
0
)f (t) = δ(t − t
0
)f (t
0
), (7.5a)
from which we can see
∞
−∞
δ(t − t
0
)f (t)dt =
∞
−∞
δ(t − t
0
)f (t
0
)dt
=f(t
0
)
∞
−∞
δ(t − t
0
)dt
168 7 Fourier Transformation of Image Data
i.e.
∞
−∞
δ(t − t
0
)f (t)dt = f(t
0
) (7.5b)
This is known as the sifting property of the impulse.
7.2.3
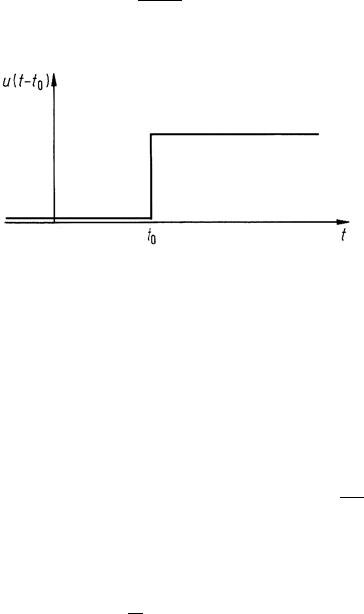
The Heaviside Step Function
Figure 7.2 shows the Heaviside step function defined by
u(t −t
0
) = 1 for t t
0
(7.6a)
= 0 for t<t
0
(7.6b)
Note that it is 1 when its argument is zero or positive, and is zero for a negative
argument. It can be seen that u(t) is related to δ(t) by
δ(t) =
du(t)
dt
Fig. 7.2. The Heaviside step function
7.3
Fourier Series
If a function f(t) is periodic with period T – i.e. f(t) = f(t + T)– then it can be
expressed as an infinite sum of complex exponentials in the manner
f(t) =
∞
n=−∞
F
n
e
jnw
0
t
,ω
0
=
2π
T
(7.7a)
in which n is an integer and the complex expansion coefficients F
n
are given by
F
n
=
1
T
T/2
−T/2
f(t)e
−jnw
0
t
dt (7.7b)
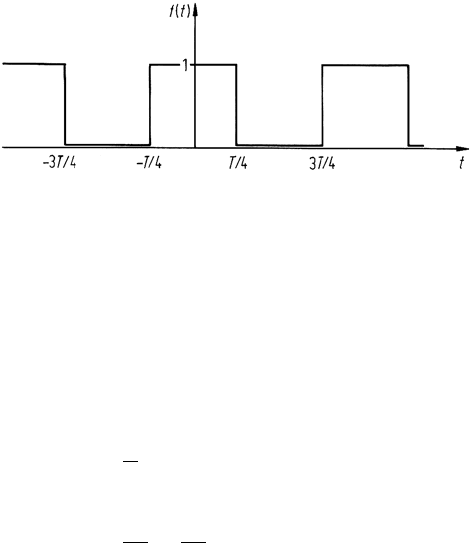
7.4 The Fourier Transform 169
Fig. 7.3. A square waveform
The expressions in (7.7) are referred to as the exponential form of the Fourier se-
ries; (7.1c) also allows a trigonometric expression to be derived (McGillem and
Cooper, 1984). Although (7.7a) is expressed in exponentials we often colloquially
talk of (7.7a) as showing the sinusoidal spectral composition of f(t). Equation (7.2)
shows that this is acceptable and quite accurate.
As an illustration consider the need to determine the Fourier series of the square
waveform in Fig. 7.3. From (7.7b) it can be seen that
F
n
=
1
T
T/4
−T/4
e
−jnω
0
t
dt
=
1
nπ
sin
nπ
2
.
This tells the amount of each of the constituent e
jnω
0
t
in (7.7a) required to represent
the square waveform – i.e. it describes its sinusoidal composition. Note that when
n = 0, F
0
= 1/2 as expected from Fig. 7.3. For n>1 the coefficients decrease in
amplitude according to 1/n. In general the F
n
are complex and thus can be expressed
in the form of an amplitude and phase, referred to respectively as amplitude and phase
spectra.
7.4
The Fourier Transform
The Fourier series of the preceding section is a description of a periodic function in
terms of a sum of sinusoidal terms (expressed in complex exponentials) at integral
multiples of the so-called fundamental frequency ω
0
. For functions that are non-
periodic, or aperiodic as they are sometimes called, decomposition into sinusoidal
components requires use of the Fourier transformation. The transform itself, which
is equivalent to the Fourier series coefficients of (7.7b), is defined by
F(ω) =
∞
−∞
f(t)e
−jωt
dt (7.8a)
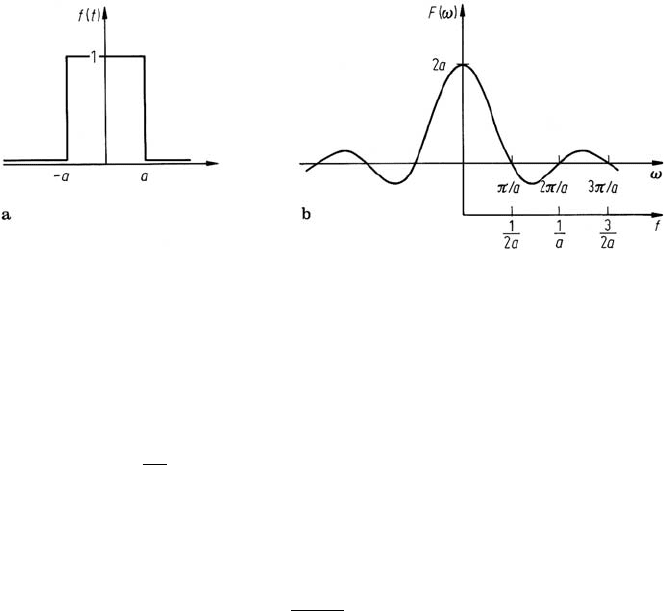
170 7 Fourier Transformation of Image Data
Fig. 7.4. a Unit pulse and b its Fourier transform
In general, an aperiodic function requires a continuum of sinusoidal frequency com-
ponents for a Fourier description. Indeed if we plot F(ω), or for that matter its
amplitude and phase, as a function of frequency it will be a continuous function of
ω. The function f(t)can be reconstructed from the spectrum according to
f(t) =
1
2π
∞
−∞
F(ω)e
jωt
dω (7.8b)
A Fourier transform of some importance is that of the unit pulse shown in
Fig. 7.4a. From (7.8a) this is seen to be
F(ω) =
a
−a
e
−jωt
dt = 2a
sin aω
aω
which is shown plotted in Fig. 7.4b. Note that the frequency axis accommodates both
positive and negative frequencies. The latter have no physical meaning but rather are
an outcome of using complex exponentials in (7.8a) instead of sinusoids.
It is also of interest to note the Fourier transform of an impulse
F(ω) =
∞
−∞
δ(t) e
−jωt
dt = 1
from the sifting property of the impulse (7.5b); the Fourier transform of a constant
is
F(ω) =
∞
−∞
ce
−jωt
dt = 2πcδ(ω).
This result is easily shown by working from the spectrum F(ω)to the time function
and again using the sifting property. In a like manner it can be shown that the Fourier
transform of a periodic function is given by
7.5 Convolution 171
F(ω) = 2π
∞
n=−∞
F
n
δ(ω − nω
0
)
where F
n
is the Fourier series coefficient corresponding to the frequency nω
o
.
7.5
Convolution
7.5.1
The Convolution Integral
In Sect. 5.3 the concept of convolution was introduced as a means for determining
the response of a linear system. It is also a very useful signal synthesis operation in
general and finds particular application in the description of digital data, as will be
seen in later sections. Here we express the convolution of two functions f
1
(t) and
f
2
(t) as
y(t) =
∞
−∞
f
1
(τ )f
2
(t −τ)dτ f
1
(t) ∗ f
2
(t) (7.9)
It is a commutative operation, i.e. f
1
(t) ∗ f
2
(t) = f
2
(t) ∗ f
1
(t) a fact that can
sometimes be exploited in evaluating the integral.
The convolution operation can be illustrated by interpreting the defining integral
as representing the following four operations:
(i) folding – form f
2
(−τ) by taking its mirror image about the ordinate axis
(ii) shifting – form f
2
(t −τ) by shifting f
2
(−τ) by the amount t
(iii) multiplication – form f
1
(τ )f
2
(t −τ)
(iv) integration – compute the area under the product.
These steps are illustrated in Fig. 7.5.
7.5.2
Convolution with an Impulse
Convolution of a function with an impulse is important in sampling. The sifting
theorem for the delta function, along with (7.9), shows
f(t)∗ δ(t − t
0
) =
∞
−∞
f(τ)δ(t − τ − t
0
)dτ
=f(t − t
0
).
Thus the effect is to shift the function f(t)to a new origin.
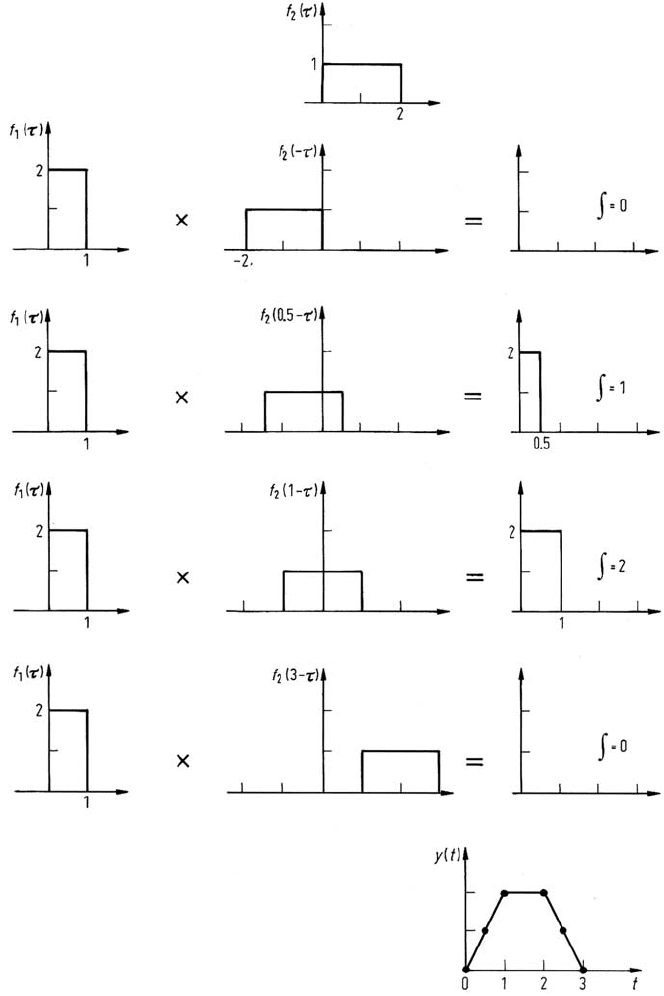
172 7 Fourier Transformation of Image Data
Fig. 7.5. Graphical illustration of the convolution operation
