Richards J.A., Jia X. Remote Sensing Digital Image Analysis: An Introduction
Подождите немного. Документ загружается.

7.7 The Discrete Fourier Transform 183
7.7.6
Computational Cost of the Fast Fourier Transform
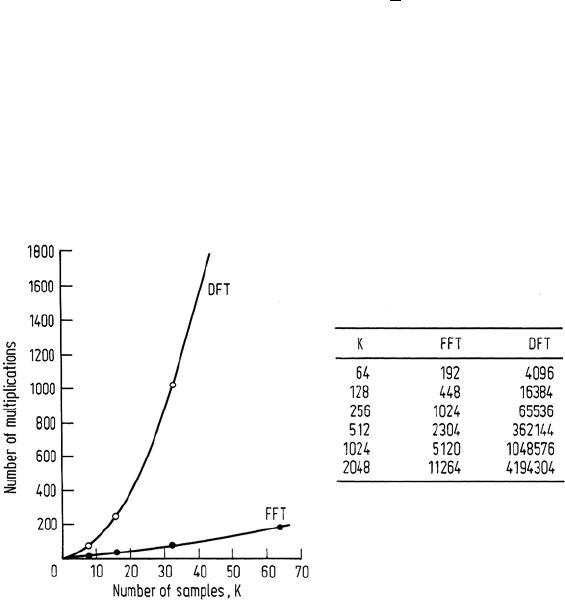
The information contained in Fig. 7.10 can be used to determine the computational
cost of the fast Fourier transform algorithm and therefore to find its speed advantage
over a direct evaluation of the discrete formula in (7.19). The figure shows that
the only multiplications required are by the values of W . While this is strictly not
necessary in the first set of calculations on the left of the figure (Since W
0
= 1, and
−W
0
=−1) it is simpler in programming if the multiplications are retained. Thus the
left hand set of computations requires K/2 complex multiplications and K additions
(or subtractions). The next column of operations requires another K/2 multiplications
as does the last set for the case of K = 8. Altogether for this illustration 3/2K
multiplications and 3K additions are required. It is easy to generalize this to:
number of complex multiplications =
1
2
K log
2
K
number of complex additions = K log
2
K.
On the basis of multiplications alone the fast Fourier transform (FFT) is seen, from
the material in Sect. 7.7.4, to be faster than direct evaluation of the discrete Fourier
transform (DFT) by a factor of 2K/log
2
K. Moreover its cost increases almost linearly
with the number of samples, whereas that for the DFT increases quadratically. This
is illustrated in Fig. 7.11.
Fig. 7.11. Number of multiplications required in the evaluation of a discrete Fourier transform
directly (DFT) and by means of the fast Fourier transform method (FFT)
184 7 Fourier Transformation of Image Data
7.7.7
Bit Shuffling and Storage Considerations
Application of the fast Fourier transform requires K to be continuously divisible by
2 (i.e. K = 2
m
as indicated above). Although other versions of the algorithm can
also be derived (Brigham, 1974) the case of K = 2
m
is most common, and is used
here.
Inspection of the flow chart in Fig. 7.10 reveals that the order of the data fed into
the algorithm needs to be rearranged before the technique can be employed. This can
be achieved very simply by a process known as bit shuffling. To do this the index
of the input samples is expressed in binary notation (see Appendix C), the binary
digits are reversed, and the new binary number converted back to decimal form, as
illustrated in the following for K = 8.
X(0) → X(000) → X(000) → X(0)
X(1)X(001)X(100)X(4)
X(2)X(010)X(010)X(2)
X(3)X(011)X(110)X(6)
X(4)X(100)X(001)X(1)
X(5)X(101)X(101)X(5)
X(6)X(110)X(011)X(3)
X(7)X(111)X(111)X(7)
Apart from the immense savings in time, use of the FFT also leads to a savings
in memory. Apart from storing the K/2 values of W
r
the entire computation can be
carried out using a complex vector of length K +1. This is because there exist pairs
of elements in each vector or column of the operation whose values are computed
from numbers stored in the same pair of locations in the previous column.
7.8
The Discrete Fourier Transform of an Image
7.8.1
Definition
The previous sections have treated functions with a single independent variable. That
variable could have been time, or even position along a line of an image. We now need
to turn our attention to functions with two independent variables, to allow Fourier
transforms of images to be determined. Despite this apparent increase in complexity
we will find that full advantage can be taken of the material of the previous sections.
Let
φ(i,j), i,j = 0,...K − 1 (7.21)
be the brightness of a pixel at location i, j in an image of K ×K pixels. The Fourier

7.8 The Discrete Fourier Transform of an Image 185
transform of the image, in discrete form, is described by
Φ(r,s) =
K−1
i=0
K−1
j=0
φ(i,j) exp [−j2π(ir + j s)/K]. (7.22)
An image can be reconstructed from its transform according to
φ(i,j) =
1
K
2
K−1
i=0
K−1
j=0
Φ(r,s) exp [+j 2π(ir + j s)/K]. (7.23)
7.8.2
Evaluation of the Two Dimensional, Discrete Fourier Transform
Equation (7.22) can be rewritten as
Φ(r,s) =
K−1
i=0
W
ir
K−1
j=0
φ(i,j) W
js
(7.24)
with W = e
−j2π/K
as before. The term involving the right hand sum can be recog-
nised as the one dimensional discrete Fourier transform
Φ(i,s) =
K−1
j=0
Φ(i,j) W
js
,i= 0, ...K −1. (7.25)
In fact it is the one dimensional transform of the ith row of pixels in the image. The
result of this operation is that the rows of an image are replaced by their Fourier
transforms; the transformed pixels are then addressed by the spatial frequency index
s across a row rather than by the positional index j. Using (7.25) in (7.24) gives
Φ(r,s) =
K−1
i=0
Φ(i,s) W
ir
(7.26)
which is the one dimensional discrete Fourier transform of the sth column of the
image, after the row transforms of (7.25) have been performed.
Thus, to compute the two dimensional Fourier transform of an image, it is only
necessary to transform each row individually to generate an intermediate image, and
then transform this by column to yield the final result. Both the row and column trans-
forms would be carried out using the fast Fourier transform algorithm of Sect. 7.7.5.
From the information provided in Sect. 7.7.6 it can be seen therefore that the number
of multiplications required to transform an image is K
2
log
2
K.
7.8.3
The Concept of Spatial Frequency
Entries in the Fourier transformed image Φ(r,s) represent the composition of the
original image in terms of spatial frequency components, both vertically and hori-
zontally. Spatial frequency is the image analog of the frequency of a signal in time.
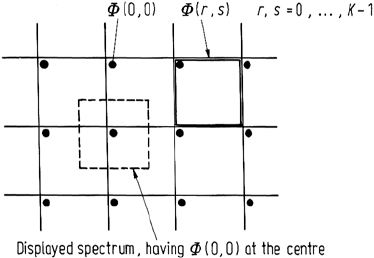
186 7 Fourier Transformation of Image Data
Fig. 7.12. Illustration of the peri-
odic nature of the two dimensional
discrete Fourier transform, showing
how an array centred on Φ(0, 0) is
chosen for symmetrical display pur-
poses
A sinusoidal signal with high frequency alternates rapidly, whereas a low frequency
signal changes slowly with time. Similarly, an image with high spatial frequency,
say in the horizontal direction, exhibits frequent changes of brightness with posi-
tion horizontally. A picture of a crowd of people would be a particular example.
By comparison a head and shoulders view of a person is likely to be characterised
mainly by low spatial frequencies. Typically an image is composed of a collection
of both horizontal and vertical spatial frequency components of differing strengths
and these are what the discrete Fourier transform indicates. The upper left hand pixel
in Φ(r, s) – i.e. Φ(0, 0)− is the average brightness value of the image. This is the
component in the spectrum with zero frequency in both directions. Thereafter pixels
of Φ(r,s) both horizontally and vertically represent components with frequencies
that increment by 1/K where the original image is of size K ×K. Should the scale of
the image be known then the spatial frequency increment can be calibrated in terms
of metres
−1
. For example the increment in spatial frequency for a 512 × 512 pixel
image that covers 15.36 km (i.e. Landsat TM) is 65 × 10
−6
m
−1
.
In Sect. 7.7.3 it is shown that the one dimensional discrete Fourier transform
is periodic with period K. The same is true of the discrete two dimensional form.
Indeed the K × K pixels of Φ(r,s) computed according to (7.22) can be viewed
as one period of an infinite periodic two dimensional array in the manner depicted
in Fig. 7.12. It is also shown that the amplitude of the discrete Fourier transform is
symmetric about K/2. Similarly Φ(r,s) is symmetric about its centre. This can be
interpreted by implying that no new amplitude information is shown by displaying
pixels horizontally and vertically beyond K/2. Rather than ignore them (since their
accompanying phase is important) the display is adjusted in the manner shown in
Fig. 7.12 to bring Φ(0, 0) to the centre. In this way the pixel at the centre of the Fourier
transform array represents the image average brightness value. Pixels away from the
centre represent the proportions of increasing spatial frequency components in the
image. This is the usual method of presenting two dimensional image transforms.
Examples of spectra displayed in this manner are given in Fig. 7.13. To make visible
components with smaller amplitudes, a logarithmic amplitude scaling has been used,
according to (Gonzalez and Woods, 1992)
D(r, s) = log [1 +|Φ(r, s)|].

7.8 The Discrete Fourier Transform of an Image 187
a
b
c
Fig. 7.13. Illustrations of Fourier transforms of images. a Single square; b Bar pattern;
c Hymap image
7.8.4
Image Filtering for Geometric Enhancement
The high spatial frequency content of an image is that associated with frequent
changes of brightness with position. Edges, lines and some types of noise are exam-
ples of high frequency data. In contrast, gradual changes of brightness with position,
such as associated with more general tonal variations, account for the low frequency
content in the spectrum. Since ranges of spatial frequency are identified with regions
in the spectrum we can envisage how the spectrum of an image could be altered to
produce different geometric enhancements of the image itself. For example, if the
188 7 Fourier Transformation of Image Data
region near the centre of the spectrum is removed, leaving behind only the high fre-
quencies, and the image is then reconstructed from the modified spectrum, a version
containing only edges and line-like features will be produced. On the other hand, if
the high frequency components are removed, leaving behind only the region near the
centre of the spectrum, the reconstructed image will appear smoothed, since edges,
lines and high frequency noise will have been deleted.
Modification of the spectrum in the manner just described can be expressed as a
multiplicative operation:
Y(r,s) = Φ (r, s)H (r, s) for all r, s (7.27)
where H(r,s) is the filter function and Y(r,s) is the new spectrum. To implement
simple sharpening or smoothing as described above H(r,s)would be set to 0 for those
frequency components to be removed and 1 for those components to be retained. Of-
ten sharpening is called high pass filtering, and smoothing low pass filtering, because
of the nature of the modification to the spectrum. Both can be implemented also with
the template methods of Chap. 5. However (7.27) allows more complicated filtering
operations to be carried out. As an example, a specific band of spatial frequency
could be excluded readily. H(r,s) can also be chosen to have values other than 0
and 1 to allow more versatile modification of the spectrum.
The overall process of geometric enhancement via the frequency domain involves
three steps. First, the image has to be Fourier transformed to produce its spectrum.
Secondly, the spectrum is modified according to (7.27). Finally the image is recon-
structed from the modified spectrum using (7.23), which can also be implemented
by rows and columns. Together these three operations require 2K
2
log
2
K + K
2
multiplications, as used in Sect. 5.4 to compare this approach to that based upon
simple templates.
7.8.5
Convolution in Two Dimensions
The convolution theorem for functions (Sect. 7.5.3) has a two dimensional counter-
part, again in two forms. These are:
If
y(i,j) = φ(i,j) ∗ h(i, j)
then
Y(r,s) = Φ (r, s) H (r, s) (7.28a)
and, if
y(i,j) = φ(i, j ) h(i, j )
then
Y(r,s) = Φ(r,s) ∗ H(r,s). (7.28b)
7.9 Concluding Remarks 189
Unlike (7.10b) there is no 1/2π scaling factor here since the spatial frequency vari-
ables r and s are equivalent to frequency f in Hz and not the radian frequency ω in
rad · s
−1
used in (7.10b).
The convolution operation implied in (7.28) is defined by (5.3). However when
digital images are of concern its discrete version is of interest. This is defined, in the
image domain, as
y(i,j) =
m
n
φ(m, n)h(i − m, j − n) (7.29)
where m and n are dummy variables. As with one dimensional convolution described
in Sect. 7.5.1 evaluation of (7.29) requires that one function, in this case the filter
function, be folded about the origin (which in two dimensions amounts to a 180
◦
rota-
tion) to produce h(−m, −n) and then delayed by variable amounts i, j. The delayed
folded version is then multiplied pixel by pixel with the image φ(m, n) and the sum
over all spectral pixels taken. This produces one pixel y(i, j) in the modified image.
Equation (7.28) implies that any of the geometric enhancement operations that
can be carried out by modifying the spectrum can also be carried out by performing a
convolution between the image and the inverse Fourier transform of the filter function
H(r,s). Conversely, operations such as simple mean value filtering with an M ×N
template as described in Sect. 5.5.1, can also be described in the spatial frequency
domain. This requires the Fourier transform of the template to be found. To do this
requires the template to be regarded as of the same dimensions as the image but with
a value of zero everywhere except for a set of M × N pixels with the appropriate
non-zero value.
7.9
Concluding Remarks
Geometric modification of an image via the frequency domain is a particularly pow-
erful technique owing to the ease with which the filter function H(r,s) may be de-
signed. The material presented in this Chapter has been intended as an introduction
to the concepts and operations involved. For the user contemplating using Fourier
domain methods, several other issues should be taken into consideration including
the use of so-called window functions. This is illustrated most easily by a return to
the material on sampling in Sect. 7.6. In that section it was noted that a sampled func-
tion could be regarded as the unsampled version multiplied by an infinite periodic
sequence of impulses. The spectrum of the infinite set of samples so produced is the
spectrum of the original function convolved with the spectrum of the sequence of
impulses as shown in Fig. 7.6. However in practice it is not possible to take an infinite
number of samples of a function. Instead sampling is commenced at a given time and
terminated after some period τ. This finite time sampling window can be considered
as a long pulse of unit amplitude and duration τ that multiplies the infinite sequence
of samples. The spectrum of the set of samples is, as a consequence, modified by
being convolved by the spectrum of the sampling window. Since the window is a
190 7 Fourier Transformation of Image Data
long pulse, its Fourier transform is as shown in Fig. 7.4 although compressed to near
the origin. If the sampling duration is long enough this approximates an impulse and
there is little effect on the spectrum. For shorter sampling times however the side-
lobes in Fig. 7.4b cause distortion of the spectrum. To minimise this effect sampling
windows different to a long pulse are sometimes used. A good consideration of these
is found in Brigham (1974).
In the preceding sections we have referred to the Fourier transform approach
as a means for geometric enhancement since it can implement operations such as
sharpening and smoothing. In the material of Chapter Five these are referred to ex-
plicitly as neighbourhood operations. To appreciate that the Fourier transform is also
a neighbourhood operation consider the flow chart for the fast Fourier transform
implementation in Fig. 7.10. If we pick one output value – i.e. one point on the spec-
trum – it can be traced back through the flow chart and be seen to have a contribution
from every one of the input samples. In a similar manner the pixels in the Fourier
transform of an image have contributions from all of the pixels in the original image.
Other transformations also exist, perhaps the most notable in the past few years
being the wavelet transform. The theory of the wavelet transformation can be quite
detailed, especially if generalised beyond the field of real functions. However, several
excellent treatments are available when the transform is to be applied to real image
data, perhaps the most accessible of which is that given by Castleman (1996).
The wavelet transform is important in so far that it provides a compact description
of signals (or images) that are limited in time (or spatial extent). The following
introduces the concept; Castleman should be consulted for details, including how
the transform is defined, and how it can be used and computed in practice. It finds
application in image compression and coding, and in the detection of localised image
features.
Suppose you listen to an organ playing a single, pure tone. As a function of time it
will be sinusoidal for as long as the key is pressed. We could, if we wished, envisage
that the sinusoid started at minus infinity and goes to plus infinity in time. It is the
simplest of all signals in terms of Fourier analysis and its Fourier series is a single
frequency (with positive and negative frequency components) as an application of
(7.7b) will show.
Now suppose you hear a piano play a single note. Rather than lasting for all time,
the time waveform of the piano note would be a time limited sinusoid. We can still find
its Fourier components – i.e. the set of frequencies it is composed of, by noting that it
is the product of an infinitely long sinusoid and the unit pulse waveform of Fig. 7.4a.
Application of (7.10b) and the material of Sect. 7.5.2 shows that its spectrum will be
the function of Fig. 7.4b but with its “origin” shifted to the frequency of the sinusoid.
The spectrum of the time limited signal is now unlimited, although it does drop off
quickly as frequency goes to plus and minus infinity.
To represent short time signals, like the piano note, by a Fourier series or trans-
form, although theoretically acceptable, is cumbersome.Yet that is a problem because
many signals (such as speech) consists of limited time signals, just as images are
also limited spatially.
References for Chapter 7 191
The invention of the wavelet – i.e. a small wavelike signal that is limited in time,
has a frequency-like property and is defined to occur at a certain time – is meant to
make the description of such signals easier and to assist in the identification of signal
characteristics that occur at particular times. In the case of images, wavelets help in
the description of properties that are highly localised such as edges and lines.
References for Chapter 7
Treatments of digital image processing in the fields of electrical engineering and computer
science invariably contain detailed considerations of the use of the Fourier transform and
frequency domain techniques for geometric modification of image data. Particular texts that
could be consulted include Castleman (1996), Gonzalez and Woods (1992) and Moik (1980).
An excellent presentation of the discrete Fourier transform, discrete convolution and the fast
Fourier transform algorithm will be found in Brigham (1974, 1988). While Brigham relates
to the one dimensional case it will be clear from the material in Sect. 7.8.2 above that it can
be used also with images.
E.O. Brigham, 1974: The Fast Fourier Transform. N.J. Prentice-Hall.
E.O. Brigham, 1988: The Fast Fourier Transform and its Applications. N.J. Prentice-Hall.
K.R. Castleman, 1996: Digital Image Processing. N.J. Prentice-Hall.
R.C. Gonzalez and R.E. Woods, 1992: Digital Image Processing. Mass. Addison-Wesley.
C.D. McGillem and G.R. Cooper, 1984: Continous and Discrete Signal and System Analysis.
N.Y. Holt, Rinehart and Winston.
J.G. Moik, 1980: Digital Processing of Remotely Sensed Images. Washington, NASA.
A. Papoulis, 1980: Circuits and Systems: A Modem Approach. Tokyo, Holt-Saunders.
Problems
7.1 Compute the discrete Fourier transform of the square wave shown in Fig. 7.3 using
K = 2, 4 and 8 samples per period of the waveform respectively. You can use the flow chart
of Fig. 7.10 to help in this.
7.2 Compute the discrete Fourier transform of the unit pulse shown in Fig. 7.4. Use respectively
K = 2, 4 and 8 samples over a time interval equal to 8a, where 2a is the width of the pulse as
shown in the Figure. Compare the results with those obtained in problem 7.1.
7.3 (a) A common technique for smoothing an image is to compute averages over square or
rectangular windows as discussed in Sect. 5.5. Consider a 3 × 1 smoothing template used to
smooth a single line of image data in the manner of Fig. 5.4. Determine the corresponding
filter function in the spatial frequency domain by finding the discrete Fourier transform of the
template. You may find the material of Fig. 7.4 to be of value.
(b) Imagine an ideal low pass filter function in the spatial frequency domain that could be
used to smooth just the lines of an image. Determine the corresponding function in the image
domain by computing the inverse Fourier transform of the ideal filter. Taking into account the
discrete pixel nature of the image, approximate the inverse transform by an appropriate one
dimensional template.
192 7 Fourier Transformation of Image Data
7.4 Verify the results in Sect. 7.5.2 graphically.
7.5 (a) The periodic sequence of impulses of (7.11) is an idealised sampling function. In prac-
tice it is not possible to take infinitessimally short samples of a function; rather the samples
will have a finite, albeit small duration. This could be modelled mathematically by replacing
(t) in (7.12) by a periodic pulse waveform. This periodic sequence of pulses can be repre-
sented by the convolution of a single pulse with the periodic sequence of impulses in (7.11).
With this in mind describe what modifications are needed to Fig. 7.6 to account for samples
of finite duration.
(b) Suppose the total period of sampling is equivalent to ten sample intervals. Describe the
effect this has on Fig. 7.6.
7.6 In Fig. 7.6a suppose the function f(t) is a sinewave of frequency B Hz. Its frequency
spectrum will consist of two impulses, one at + B Hz and the other at −B Hz. Produce the
spectrum of the sampled sinusoid if only three samples are taken every two periods. Suppose
the waveform is then reconstructed by feeding the samples through a low pass filter that will
pass all frequency components unattenuated, up to 1/2T Hz, where T is the sampling interval,
and will exclude all components with frequencies in excess of 1/2T Hz. Describe the shape of
the reconstructed signal; this will give an appreciation of aliasing distortion.
