Raabe J. Hydro power - the design, use, and function of hydromechanical, hydraulic, and electrical еquipment
Подождите немного. Документ загружается.

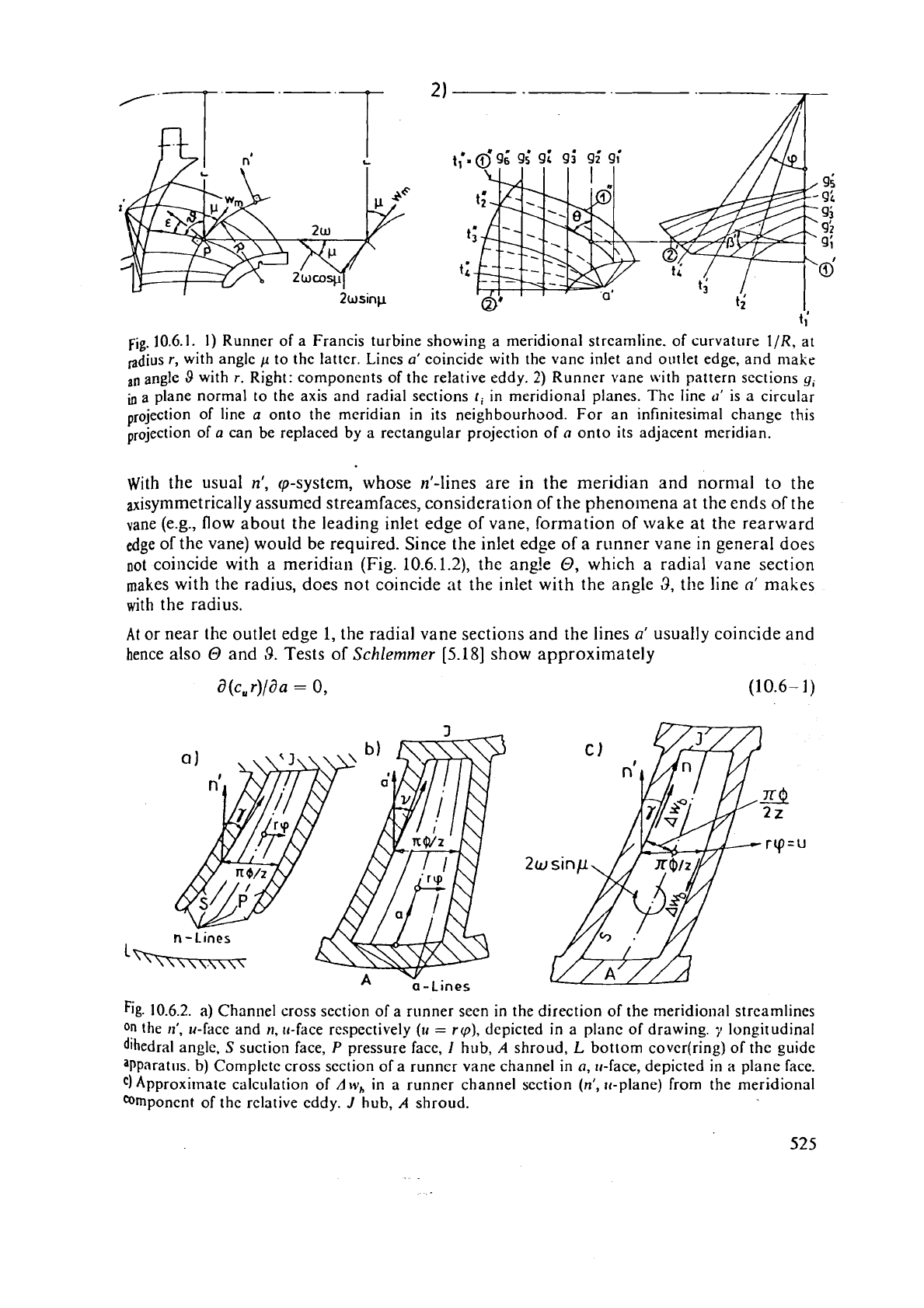
Fig. 10.6.1. 1) Runner of a Francis turbine showing a meridional streamline. of curvature
1/R,
at
ladim
r,
with angle
p
to the latter. Lines
a'
coincide with the vane inlet and outlet edge, and make
an
angle
9
with
r.
Right: components of the relative eddy.
2)
Runner vane with pattern sections
gi
a
a
plane normal to the axis and radial sections
ti
in meridional planes.
The
line
0'
is a circular
of line
a
onto the meridian in its neighbourhood. For an infinitesimal change this
projection of
a
can be replaced by a rectangular projection of
o
onto its adjacent meridian.
With the usual
n',
cp-system, whose n'-lines are in the meridian and normal to the
axisymmetrically assumed streamfaces, consideration of the phenolnena at the ends
of
the
vane
(e.g.,
flow
about the leading inlet edge of vane, formation of wake at the rearward
edge of the vane) would be required. Since the inlet edge of a runner vane in general does
not
coincide with a meridian (Fig. 10.6.1.2), the angle
0,
which a radial vane section
makes with the radius, does not coincide at the inlet with the angle
3,
the line
n'
makes
with the radius.
At
or near the outlet edge
1,
the radial vane sections and the lines
a'
usually coincide and
hence
also
O
and
3.
Tests of
Schlemmer
[5.18]
show approximately
Fig. 10.6.2. a) Channel cross scction of
a
runner seen in the direction of the meridional streamlines
on
the
n',
u-face and II,II-face respectively
(u
=
rcp),
depicted in a plane of drawing.
;l
longitudinal
dihedral angle,
S
suction face,
P
pressure face,
I
hub,
A
shroud,
L
bottom cover(ring) of the guide
apparatus.
b)
Cornplcte cross section of a runncr vane channel in
a,
11-face, depicted in a plane face.
C)
Approxitnate calculation of
Aw,
in a runner channel section
(n',
ri-plane) from the meridional
component of the relative cddy.
J
hub,
A
shroud.

nhcre
c,,
is the whirl component
of
absolute flow and
r
the distance from thc rotor
Compnriitive
C~IICI!~~
lions
show,
that the last relation may be sl~bstituted for the
st
equatiorl of motlon nt-cded for the sllroud to hub distribution of velocity. This is adva
geous since the strict relation contains the curvature
1/R
of the n~eridional stream]
and the convective acceleration dw/ds of relative flow as unconvenie~~t terms.
The
streamface is prclimin;lrily assumed to be axisymmetric. Later on the twist
of
streamface is accounted for as
a
correction of the second order and this is in agreemen<
with tests of
Schlem~~ler
[5.18].
The loss is introduced as a stream-line-linked term.
.
b
10.6.2.
Iist
of
symbols
used: (Fig.
10.6.3
to
6)
~7,
=
aa/dn; a'-coordinate in the meridian making an angle
E
with a normal to the stream
face ancl an angle
3
with the radius
r,
cr'
is the projection of a onto the meridian, with
which it makes an angle
v;
a-coordinate along the trace of the vane surface, which makes
an
angle
7r/2
-
v
with the circumference; n'-coordinate in the meridian normal to the
streamline, which makes an angle
y
with line n along the vane (longitudinal dihedral
angle); 11-coordinate along the vane trace in a surface normal to the axisymmetrical
streamface; e-internal energy term;
f
=
n' tan
y;
s
-coordinate along the meridional
"'.
streamline; s,-coordinate or length in the peripheral direction, 11-peripheral coordinate or
I+
s,;
11,
=
au/i?,t;
117,-relative velocity component normal to
w
caused by the twist of the
streamface by the meridional corriponent of relative eddy; /3'-angle of pattern section with
the periphery;
;I-longitudinal dihedral angle of vane trace n in the
11,
q-face with
n';
p-acute angle of relative velocity
IV
with the periphery; &-angle between a' and n' in the
mcridiar,; O-angle of the radial vane section with the radius; $-angle of
a'
and
r
in the
meridian;
11-angle of the meridional streamline with the radius; v-angle of a' with
a
in the
a,
9-face; q-azimuth; ;(-angle of a with n'; $-angle of
s,
with
(I;
@-contraction coefficient.
Sufices: 1-suction edge of runner vane; 2-pressure edge of runner vane; 1M-channel centre
line;
u-peripheral direction; s,-due to the direction of the meridional streamline; uO-unit
vector in the
u-direction; i-the ith step.
10.6.3.
Complitation
of
relative velocity
distribution
10.6.3.1.
In
the
peripheral
cp-direction
Once the angles
/I'
of
the pattern section,
O
of the radial section,
11
of the lneridional
streamline are known for a flow along the vane surface, then the angle
P
of the relative
flow with the periphery follows from
(6.5-
13)
as
B
=
arc tan[sin
O
tanP/sin(O
+
p)].
(10.6-2)
To simplify the derivation of the velocity distribution, which obviously is not influenced
by
the orientation of the runner shaft, the latter is assumed as vertical.
Consider a unit mass of
fluid of circumferential length
rdq
(Fig.
10.6.3.1).
At the rotating
frame
of
reference, the following forces act on this mass in the peripheral q-direction
a)
-(tie)
ap/(l-alp)
due to the tangential pressure gradient
b)
20 cos
pw
sin
p
due to the Coriolis force in the streamface
c)
w'
sin
B/R,
due to streamline curvature
1/R,
in the streamface
d)
wawlds
cos
due to the convective acceleration
awlas
in the direction of the relative
streamline
(s).
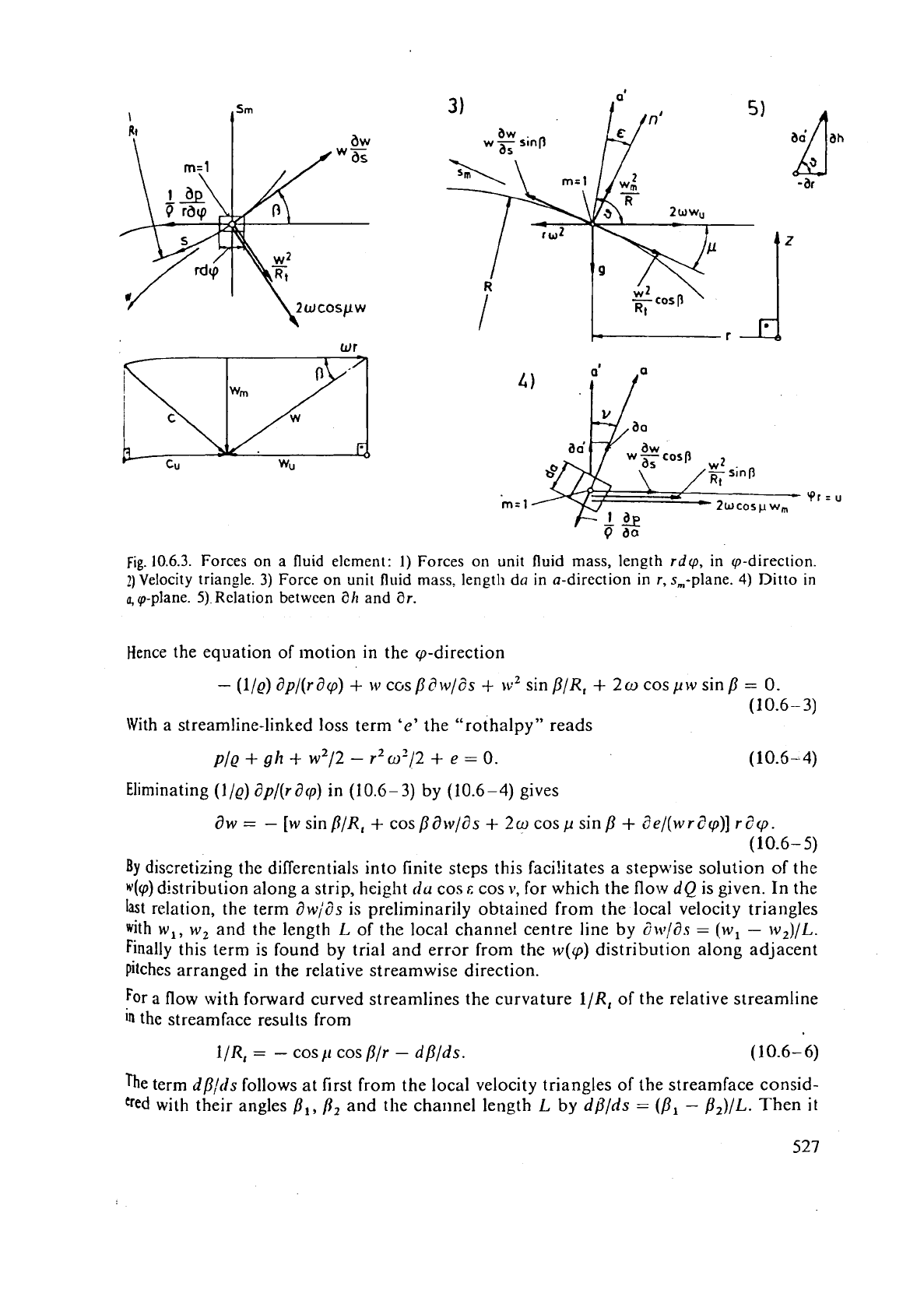
Fig.
10.6.3.
Forces on a fluid element:
1)
Forces on unit fluid mass, length rdy, in y-direction.
1)
Velocity triangle.
3)
Force on unit fluid mass, length da in a-direction in r, s,-plane.
4)
Ditto in
49-plane. 5)Relation between
ah
and ar.
Hence the equation of motion in the cp-direction
-
(lie)
ap/(rdcp)
f
w
cos
pi?w/ds
+
\v2
sin
P/R,
+
2w
cos
pw
sin
p
=
0.
(1
0.6-
3)
With a streamline-linked loss term
'e'
the "rothalpy" reads
Eliminating
(l/e) apl(r8rp)
in
(10.6-
3)
by
(10.6-4)
gives
By
discretizing the differentials into finite steps this faci!itates a stepwise solution of the
~(9)
distribution along a strip, height
du
cos
E
cos
v,
for which the flow
dQ
is given. In the
last relation, the term
aw/i?s
is preliminarily obtained from the local velocity triangles
with
w,,
w,
and the length
L
of the local channel centre line by
21vla.s
=
(w,
-
w2)/L.
Finally
this term is found by trial and error from the
w(q)
distribution along adjacent
pitches arranged in the relative streamwise direction.
For
a
flow with forward curved streamlines the curvature
1/R,
of the relative streamline
In
the streamface results from
The term
dplds
follows
at
first from the local velocity triangles of the streamface consid-
ered
with their angles
P,,
P,
and the channel length
L
by
ddlds
=
(/I,
-
P,)/L.
Then it

rnay
bc
improved by
(
10.6-2),
from which
tip/,ls
=
[cos2 fiIsi11
(O
+
101
-
{[sin(@
+
11) cos
O
-
cos(O
+
p) sin
01
tan
PI
dO/ds
+
[sin(@
+
p)
sin @/cos2
p']
d/?'/ds
-
sin
O
tanp' cos(@
+
p) d~i/ds).
(10.6-7)
.*
In
the
assumed flow along the vane, thc derivatives of the an~lcs
8,
P',
11
(here signified
by
s)
.with respect to
s
lollow by dxlds
=
(dxldr) drlds
+
(irslaz) dzltls, where z is
the
coordinate along the machine axis. The values ax/&-, ax/az herc follow from the given
pattern and radial sections of the vane and the streamline pattern. The derivatives
dr/ds,
dzlds result from Figs. 10.6.3.1 and 10.6.3.3 by
drlds
=
(drlds,) dsm/ds
=
-
cosp sin p;
ilz/cls
=
(dzlds,) dsm/ds
=
-
sin
!i
sinp.
With these relations and (10.6-7), the curvature term l/Rt is reduced to known figures
like aplar,
aIl/az,
ap'ldr,
ap'laz, d@/ar, a@/az from the elevation and plan of the vane
design with its pattern and radial vane sections.
The loss term
de/()ordcp) may be converted into kaw/(r?cp) by introducing
r
=
kw2/2,
with
k
as an empirical coef'licient.
10.6.3.2.
In
the
shroud
to
hub
(=
a)
direction
Consider a unit mass of fluid of length da in the direction
n
(Fig. 10.6.3.3).
111
the following
the centrifugal force
w2r due to rotation and the gravity
g
are omitted, since they cannot
influerice the desired velocity distribution. Then in the rotating frame of reference, the
following forces act on this mass in the shroud to hub (a)-direction:
a)
-
(I/g)
dplaa due to the pressure gradient in the n-direction
b)
20
(\v,
cos3 cos
v
+
w,
cosp sin\,) due to the radial and tangential components of
Coriolis force, where
14,
=
\V
cos
P,
W,
=
w
sin
P
C)
(\v2,'R,)
(sin
P
sin
Y
-
cosp cos
v
sin E) due to the tangential and meridional components
of centrifugal force under a forward curved streamline with the curvature
l/Rt in the
axisymmetric streamface.
dj
~t~(d\vjSs) (cosp sin
v
+
sin jl cos
v
sin E) from the tangential and meridiorial compo-
nents of body force due to the convective-acceleration
in
the streamwise direction of the
relative flow.
e)
(lv:,/R)
cos~ cosv from the componer~t of centrifugal force due to the curvature 1/X of
tile meridional streamline.
The equation of motion resulting from these forces after substituting the pressure gra-
dient term
a)
from the "rothalpy"
(10.6-4),
differentiated with respect to
a,
but ignoring
r20'/2
and the
ylt
term, yields the following relation for the distribution of
w
in the
a-direction
aw
=
-
(w
{sin2
/I
cos
v
sin($
+
p)/R
-
(cosp cosjllr
+
dplds)
.
[sin
p
sin
v
+
cos
p
cos
v
.cos
(9
+
p)]}
+
2co(cosjlcos9 cosv
+
sinPcosp sinv)
(10.6-8)
+
(awlas) [cosp sin
v
-
sinp cos
v
cos(9
+
p)]
+
ae/(w
Gu))
2a.

To
obtain this, use was made of
(10.6-6)
and the following relation from Fig. 10.6.3.3
cs
9
+
p
-
~12.
I
:
10.6.3.3.
Method
of
solution with exact
w(a)
distribution
For
a
practicable stepwise solution, the last relation has to be discretizcd in the form
*here wM is the relative velocity along the channel centre line whereas
A
and
B
follow
horn
(
10.6-8). There again the term ae/(waa) may be brought into the form
k2\v/?a.
fie computation starts within
a
strip of tangential length
r(n)
Aq
crossing the a, cp-face
tonsidered in
a
direction along the centre line from shroud to hub. The chosen angular
dcrement
Aq
must be much smaller than the unobstructed pitch
2
n
@r/z
of the channel.
4
being the contraction coefficient due to the thickness of the vane and its boundary
layers.
11
seems advisable to estimate
w,
on the basis of the potential flow pattern on the shroud
11
a
=
0. Whence
w(a)
can be determined stepwise and in the first instance
by
(10.6-9)
dong
the aforementioned strip in the a'-direction. The flow passing this strip results from
continuity as
ai
AQ
=
Acp
j
r(a) wM(a) cosv(a) cosc(a) da,
(10.6-
10)
o=o
where
ai
is the coordinate a at the hub. Next compare
d
Q
with the flow
A
Q, passing this
suip
by means of an axisymmetric potential flow using the mean contraction coefficient
4."
between shroud and hub and the given flow
Q.
Thus
11
is assumed that the more correct flow through this strip corresponds to the last value.
To
improve the results, all the velocities w,, preliminarily computed have to be multi-
plied by the quotient
3
=
A
Q,/AQ. Hence the second approximation of ?he vclocity along
the centre line
w,,
results from the first approximation
w,,
,
by
w,,
=
[
w,,
,
.
Once w,, is determined finally by the above method, the distribution of w
in
the
direction may be implied on the base of (10.6-5) now written as
With the aid
of
this stepwisely obtained w(a,cp)-distribution, check
by
means
of
the
continuity relation
dthe
flow
Q,
through a channel corresponds to the prescribed vaiue Q/z. In general Q,
may
deviate from Q/z. Then
5
=
Q/(zQ,) may differ from 1. Hence the second approxima-
tion
of velocity (now including also the ~(q) distribution and hence denoted
by
w,,)
is
obtained from the first approximation
w,
,
by w,,
=
<
w,
..
,n
ed
values such as Obviously any step changes the original flow pattern and the flow-I. k
K
R
=
ap/6sm. Moreover the entry in the above calculation of the
~((1)
distribution
quires the values
A
and
B
as function
of
0.
For this purpose some geometrical relations
are
required treated in the next section.
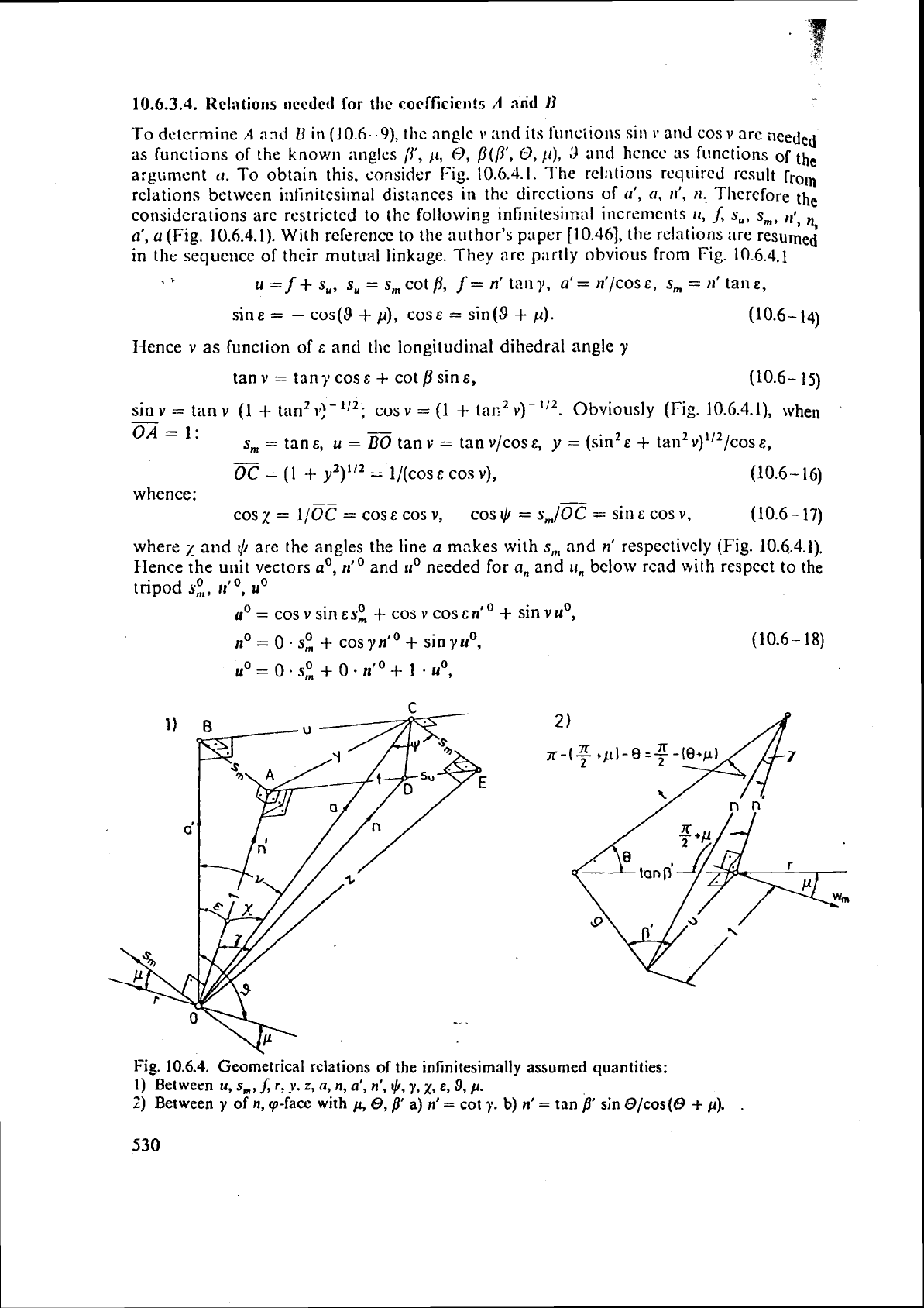
10.6.3.4.
Relations
nccdctl
for
tl~c
cocfficic~~!~
A
arid
11
To
detcrrnine
A
and
U
in
(10.6
9),
the
angle
r
and
its
filaciioils sill
r
aid
cOs
v
arc ileeded
as functions of
the
known
angles
$',
11,
0,
P(/?',
O,
I(),
3
and hcncc as functions of
the
argument
tr.
To obtain this, corlsidcr Fig. 10.6.4.1. The rcl:llions required rcsult
rroln
relations between i~~finitcsi~nal distances in thc
directions
of
a',
a,
lt',
11.. Therefore
the
consirlerations arc restricted to the following infi~litesi~nal increments
rr,
/,
s,,
s,,,,
,,;
n.
LI',
u
(Fig.
10.6.4.1). With refcrencc to the author's paper [10.46], the relations are resumed
in the sequence of their mutual linkage. They
arc
partly obvious from
Fig.
10.6.4.1
.
.
u
=
f+
s,,
s,
=s,,cotp, f=nl tally, a'= nl/cos&,
S,
=)I'
tane,
Hence
v
as
function of
E
and
the longitudinal dihedral angle
y
sin
v
=
tan
v
(1
-t-
tan2 1.)-'I2; cos
v
=
(1
+
tan2 v)-'/~. Obvi~~sIy (Fig. 10.6.4.1),
when
,
-
OA=
1:
-
z
112
s,
=
tan E,
u
=
80
tan
v
=
tan
vlcos E, y
=
(sin2&
+
tan v)
/cos
E,
-
OC
=
(1
+
y2)'I2
='I/(COSE
COSV),
(10.6- 16)
whence:
-
cos
4
=
1/oc
=
cos
E
cos
v,
cos
t,!j
=
s,,/OC
=
sin
E
cos
V,
(10.6- 17)
where
and
{h
are the angles the line
a
mzkes with
s,,
and
n'
respectively (Fig. 10.6.4.1).
Hence rhe
unit vectors a', n" and a0 needed for
a,
and
u,
below read with respect to the
tripod
s:,,
rt'
',
u0
uO=
cosvsin~s;
+
COSVCOSE~~~+
sinvuO,
Fig,
10.6.4.
Geometrical relztions of
the
infinitesimally
assumed
quantities:
1)
Between
u,
s,,
I,
rt
y.
z,
a,
n,
a',
n',
I),
y,
X,
E,
9,
p.
2)
Between
y
of
n,
cp-face
with
,u,
0,
a)
n'
=
cot
7.
b)
n'
=
tan
8.
sin @/cos(Q
+
p).

ghcnce da/dn and au/dn as scalar products
da/an
=
a,
=
cos(a, n)
=
aOnO
=
cosy cos
v
cos
E
+
sin
v
sin
7,
au/dn
=
u,
=
cos(u, n)
=
uOnO
=
sin y,
(10.6- 19)
From Fig. 10.6.4.2 cot
y
=
tan(@
+
p) tanp.
10.6.4.
Simplified relation for shroud to hub distribution
muation (10.6- 1) may be converted by means
of
the relation obvious from the velocity
triangles (Fig. 10.6.3.2)
cy
=
or- wcos/I,
(10.6- 20)
by
means of the evident relations (Fig. 10.6.3.3 and
5)
as,/aa
=
cos
@
=>
sin
E
cos V,
(10.6-22)
both
the last of which result from (10.6- 17), and by means of the following relation, from
(10.6-21) through (10.6-23) and
E
=
9
+
,u
-
7112:
drlda
=
(arlds,) ds,,,/da
+
(arlan') dn'lda
=
-
cos
v
cos
9,
(10.6-24)
into the following differential equation
aw
=
-
[w(tan pdp/da
+
cos
v
cos 3/r)
+
2
o
cos
v
cos S/cos
fl
da.
(10.6-
25)
The
structure of this equation is the same in principle as that of relation (10.6-8). But for
the
absence of the curvature term
w
sin2
p
cos vlR and the term awlds due to convective
acceleration, the last relation is much simpler than (10.6-8). This relation contains the
expression
dQ/da. This can be related to the values dO/da, dg'lda, dpjda known from the
geometry of the vane, as will be shown later, in a manner analogous to that applied to
@Ids
in (10.6-7). The assumed flow along the vane prohibits any derivative in the
pdirection. Hence
dplda
=
(dplar) rlrlda
+
(ap/az) dzlda,
(10.6
-
28)
where z is the upwardly oriented coordinate along the runner axis. The derivatives
aO/?r,
@/az may be obtained from the radial vane secti0r.s in the elevation, the derivatives
EB'ldr, 3,Yldz from elevation and plan of the pattern sections and the derivatives i?p/Cr,
3p/az
from the pattern of the meridional streamlines. The coefficients dr/da and azl6a
n
the last relations are evident from Figs. 10.6.3.3 and
4
as
drlda
=
(drlda') da'lda
=
-
cos
9
cos
v,
(1 0.6
--
29)
dzlda
=
(dzldn') da'lda
=
sin
8
cos
v.
(1 0.6
-
30)

U
Fig.
10.6.5.
1)
Coniputcd relative velocity from the suction face
S
to the pressure face
P,
and
from
the shroud
,4
to the hub
J
in an unrolled mean
a,
u-plane
(u
=
rcp),
obtained by the exact relation
(
10.6-8)
----
and by the approximate relation
(10.6-25)
----.
2)
Twibt of the mean stream surface,
conlputed
by
(10.6-31)
through the exact relation
(10.6-25)
-
and the approximate relation
(1
0.6-25)
----.
S
suction face;
P
pressure face,
M
mean stream surface,
itf,
-,
-
mean
a,
u-face,
3)
Mcasurcd mcridional streamlines al~ng the outer edge of the boundary laycr on the suction and
the pressure face (see
Fig.
10.3.22)
aficr
Schlemmer
[5.15].
Measurcmcnts and calculations for bep
of
a
Fr
with
g
H
=
35,8
m2js2,
Q
=
0,324
m3/s,
o
=
31,6
radls;
D
=
0,455
n~.
Fig.
10.6.5.1
shows the distribution of
IV
in the
n,
cp-face for certain data
Q,
gH,
a,
alternatively computed with the relations (10.6-25) and (10.6-8).
ti
similar procedure
was
nude with the twist of stream faces treated in 10.6.5. The results differ slightly.
10.6.5.
The twist
of
the stream face
in
the runner channel
Schleini~ter's
tests in the author's lab at TU h4iinchen showed that even at bep the
orientation of the relative velocity in
the flow near to the outer edge of the boundary layer
of
a
runner vane hints at a twist starting from the runner entrame and causing
a
deviation
from the axisymmetric streamface assumed, (Fig. 10.6.5.3)
I10.461. An attempt was made
in the pertinent doctoral thesis
f5.181 to explain the effect. As the velocity was measured
outside the boundary layer, the reason for the effect seems to be the meridional compo-
nent of the relative eddy (Fig. 10.6.6). This holds especially, as in this case the measured
twist was in the same sense as this relative eddy component.
The consequences are now considered under the assumption, that according to the tests,
the twist is small so that it may be superimposed on the axisymmetric flow as an
effcct
of the second order. Consider an elementary parallelogram in an
n',
cp-face normal to the
streamface. One pair of its sides is orientated in the tangential direction and the other pair
parallel to the vane trace
i~.
This makes the longitudinal dihedral angle
y
with
n'
normal
to the st ream face
(Fig.
10.6.6.1).
According to the assumption of an absolute irrotational flow, the meridional component
of
the relative eddy is
20
sinp and normal to the parallelogram.
It
influences first the
relative whirl component
w,.
Also a small velocity
M,,
must
be
introduced in the direction
n
and normal to
~v.
This varies in the tangential direction.
Stokes'
theorem gives
-
dw,/(r
dcp)
-
d(w
r
cos
P)/(r an)
=
2o
cos
y
sin
b.
(10.6-
31)
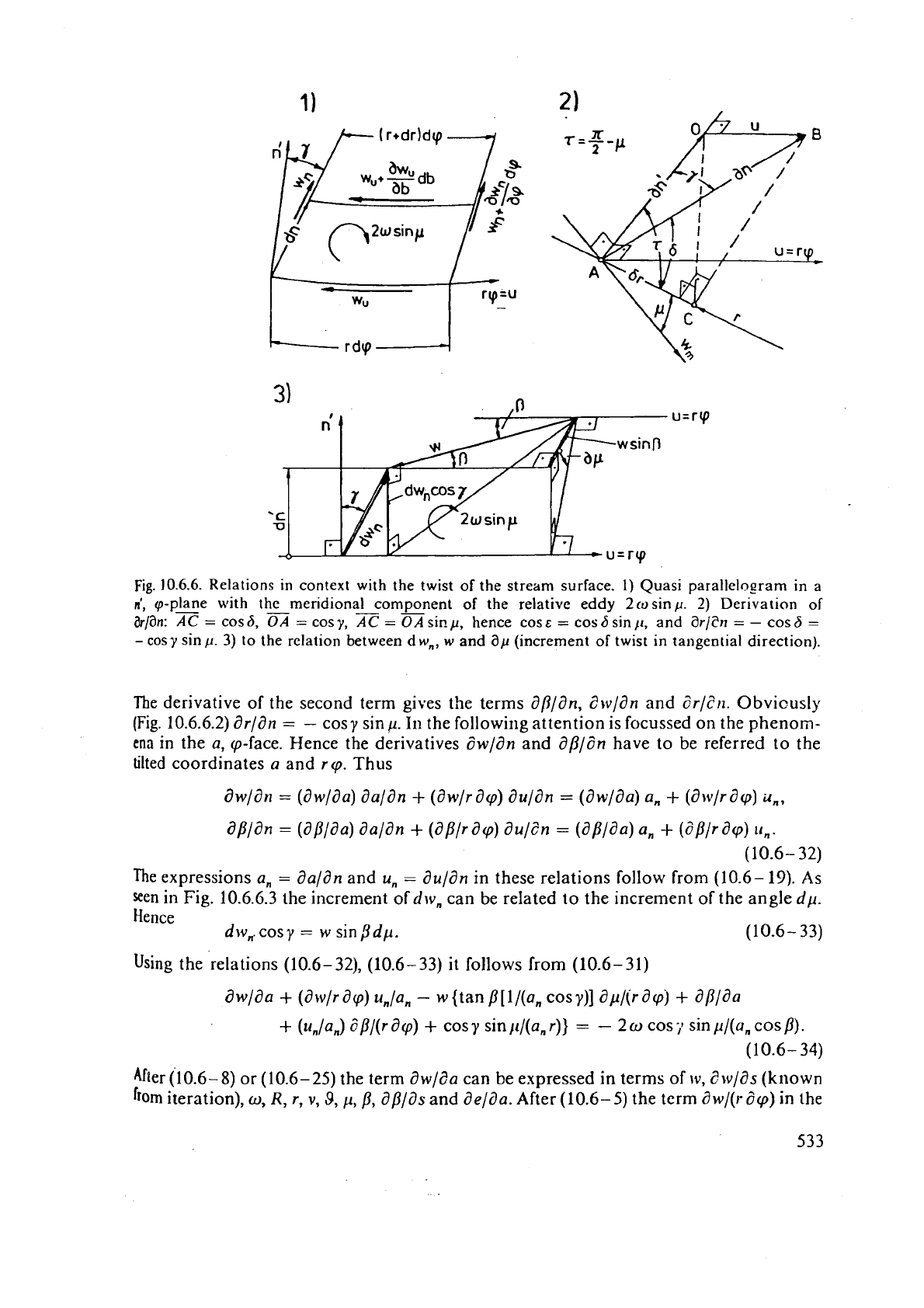
Fig.
10.6.6.
Relations
in
context with the twist of the stream surface.
1)
Quasi parallelogram in
a
n',
9-plane
-
with the meridional
-
component
-
of the relative eddy
2co
sinp.
2)
Derivation of
&/an:
AC
=
cos
6,
=
cos
y,
AC
=
OA
si~.
p,
hence cos
e
=
cos
6
sin
11,
and
i3rlSn
=
-
cos
6
=
-
cosy
sin
p.
3)
to the relation between dw,, w and
ap
(increment of twist in tangential direction).
The
derivative of the second term gives the terms
ap/an, l?~/dn
and
i?r/?rt.
Obvicusly
(Fig.
10.6.6.2) dr/dn
=
-
cosy sin
p.
I11
the followi~lg attention is focussed on the phenorn-
cna
in the
a,
cp-face. Hence the derivatives
awlan
and
dp/dn
have to be referred to the
tilted coordinates
a
and
rcp.
Thus
ag/dn
=
(dplaa) aaldn
+
(dplracp) au/8n
=
(aglda) a,
+
(dplrdcpj
11,.
(10.6-
32)
The
expressions
a,
=
da/dn
and
u,
=
au/dn
in these relations follow from
(10.6- 19).
As
seen in Fig.
10.6.6.3
the increment of
dw,
can be related
to
the increment of the angle
dp.
Hence
dw,.cosy
=
w
sinpdp.
(10.6-33)
Using the relations
(10.6-32), (10.6-33)
it follows from
(10.6-31)
awlaa
+
(d\v/r
dcp)
u,/a,
-
w
{tan
P[l/(a,
cos
y)]
ap/ir dcpj
+
dP/da
+
(u,/a,) Zp/(r
aq)
+
cos
y
sin
ji/(a, r))
=
-
2
o
cos
7
sin
,U/(U,
cos
p).
(10.6- 34)
After
(10.6-8)
or
(10.6-25)
the term
awlaa
can be expressed in terms of
w,
i?w/as
(known
from
iteration),
o,
R,
r,
v,
9,
p,
p,
dp/ds
and
de/da.
After
(10.6-5)
the term
dw/(r dp)
in the

last relation can I,c related to
w,
/I,
li,
or accordirlg
to
(10.6-6) to
/I.
r,
ji,
abla
by
(1
0.6- 7). Hcncc with the :lssurnptiol~
d/I/(rLl(p)
=
0, (10.634)
is
n
dilTercntinl equation
for
tlle con~putatio~~
or
the twist
dll/(ri?cp)
of tlie strcrlm fxe.
From Fis. 10.6.5.3a
it
is seen that at bep according to mcasure~~ic~lts
dlr
-
100.
Ancr
writing down (10.6-33) for
11
=
30" and
y
=
20",
the
quotient
d~v,/~v
beconles
-
0,I.
F~~
a simple check of this result assume thc channel section in the
rr,
p-fact
to be a Ilarrow
par;illelogram. tiere tile eddy
20
sing prod~ces mainly a velocity along the long side.
B~
clefinition of curl (Cap.
5.2)
with
wr
=
w/l.
nearly:
A
~v,/~v
=
4
n(b
COSY
sin
ll/(z?.).
For
2
'15
vanes;
@
=
0,7;
1
=
1,5;
y
=
20":
A
w,/w
=
0,12 in fair agreement with the above.
Measurements of
&hc
relative and partially the absolute flow field also in a Francis turbine
were carried out by
Biir
[5.17] and
Scl~lerilriter
[5.18] by means of time-averaging instm-
ments. Dynamic measurements of relative and partly absolute flow in a Francis turbine
were carried out by
Furtner
[9.141],
hlollenkopf
(9.461, and
Gericl~
[9.133].
10.6.6.
The state of knowledge
in
predicting
the relative
flow
Experimental and nunlerica! investigations of the behaviour of a reversible pump-turbine
runner at design point and off design point were carried out by
Verttronr, Mirandola
and
iVnvnr.ro
[lo. 1781.
Cat-iae,:a/e
et al. [lo. 1791 made a theoretical and experimental analysis,
Korcinn
[6.44] an
exp1:rimental investigation on
il
semi-axial pump, whose flow pattern niay be approxima-
tely equated to that in a Francis pump-turbine in pumping
mode.
A
theoretical approach of quasi-three-dimensional flow in a semi-axial machine was
presented by
Ererneef
and
Philibert
[10.180]. A further theoretical approach
of
ideal
steady relative flow in Francis turbines was treated by
Voetter
[10.181].
A
critical compar-
ison between
2tl and
3d
calculations, and corresponding non-dynamical, and time-
averaged dynamic measurements of the relative flow in a certain
FT
was presented by
Pfoerti~er
[6.22], and his conclusions were in favour of 2d methods.
Another impulse to calculate the steady three dimensional
(=
3
d)
ideal flow in stationary
or rotating ducts
came from
Wu
[10.182]. He uses the obvious fact, that any streamline
can be considered as the intersection of two types of flow planes, represented by the
streamfunctions
Y/, and Y2, from which, e.g.
Yl
may be adaptable to the runner blade
faces and
Y2 to the faces of shroud and hub. Thus
JV
=
grad
Yl
x
grad
Y2.
'
(10.6-35)
This vectorial equation is identical with three scalar equations. They read, in the case
of
cylindrical coordinates
z,
r,
cp
as
Putting these components
of
relative velocity into the equations of motion for the
rotating frame of reference
yields three quadratic differential equations for the uilknown
stream functions
Yl,
Y2.
In
the
case of
an
irrotational absolute
flow,
the equation
of
