Пьявченко Т.А., Финаев В.И. Автоматизированные информационно-управляющие системы

Подождите немного. Документ загружается.

131

2.5.1. Проверка на достоверность. Благодаря выполнению этого

алгоритма, обнаруживаются и устраняются импульсные помехи,

выявляется обрыв или короткое замыкание в канале связи и

формируется сообщение о нарушениях оператору-технологу. В

зависимости от того, меняется ли технологическая переменная во

времени или остается постоянной, требования по проверке будут

отличаться. Если переменная по ходу технологического процесса

изменяется и

известна допустимая скорость этого изменения, то

проверку на достоверность осуществляют по условию:

ik i(k-j)

x-x

, (53)

где

i - номер датчика; k - номер отсчета; V

- допустимая скорость

изменения технологической переменной

; T

– временной интервал

проверки на достоверность по скорости изменения, связанный со

временем опроса датчиков

опр

соотношением:

vi опр

T=jT

. (54)

Величина

j не должна быть меньше трех, поскольку заключение о

недостоверности сигнала принимается после трех кратного нарушения

условия (53).

В случае постоянства технологической переменной

должны быть

известны верхняя

и нижняя XH

допустимые границы её

отклонений, определяемые, обычно, из технологических инструкций и

по условиям эксплуатации. Так, например, допустимые изменения

температуры перегретого пара в парогенераторе составляют (460 –

550)

С при номинальном значении 540

С [60]. Следовательно, выход

единичного измерения или серии измерений за указанные границы

должен рассматриваться как нарушение. Чтобы его обнаружить,

необходимо выполнить проверку следующего неравенства:

iik i

XH < x < XB

. (55)

Проверка сигналов на достоверность заключается в следующем:

если условия (53) или (55) не выполняются, то содержимое счетчика

нарушений увеличивается на 1, неверное значение показаний датчика

заменяется

последним достоверным, и проверяется следующее

показание датчика с

более мелким шагом опроса. Процедура проверки

повторяется. Если трижды подряд не выполняются неравенства (53)

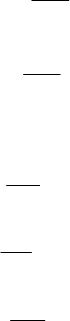
132

или (55, то по знаку разностей (

- x

ik(k-j)

) или (x

- XG

) принимается

решение о нарушении связи в

i-м канале (при отрицательном знаке)

или неисправности датчика этого канала (при положительном знаке).

Во второй скобке

- та граница, по которой не выполняется условие

(55). После обнаружения ошибки фиксируется время нарушения, его

причина и включается резервный канал или резервный датчик.

2.5.2. Сглаживание. Обычно по ходу технологических процессов

возникают помехи с частотами, близкими или равными частотам

полезного сигнала. Примером такой помехи могут быть погрешности

измерения. Устранить их аппаратными фильтрами не удается, но

можно ослабить, и весьма существенно, программным путем, реализуя

алгоритм скользящего или экспоненциального сглаживания.

Оценим каждый из них с точки зрения расхода памяти

быстродействия, а также покажем, как следует вычислять параметры

сглаживания перед запуском этих программных модулей.

Под быстродействием рассматриваемых алгоритмов будем

понимать готовность каждого из них выдать

1-е значение сглаженного

сигнала с заданным уровнем ослабления помехи

Алгоритм

скользящего среднего определится формулой:

∑

ik i(М +k-

)

j=1

xc = x

, (56)

где

– параметр сглаживания, величина которого определяет

количество отсчетов

ij i

x (j=1,M)

, взятых для вычисления одного

сглаженного значения

Раскроем формулу (56) для частных значений

k, а именно:

i1 i1 i2 i(M )

xc = (x + x + ...x )

, (57.а)

i2 i2 i3 i(M +1)

xc= (x+x+...x )

, (57.б)

i3 i3 i4 i(M +2)

xc= (x+x+...x )

(57.г)

и т.д.

Принцип скользящего окна поясняется формулами (57.а) - (57.г), из

которых следует, что для вычисления очередного сглаженного

значения записанная в

ячейках памяти информация сдвигается

133

влево, и в освободившуюся ячейку заносится новый отсчет датчика.

После чего выполняются процедуры суммирования

отсчетов и

умножения на коэффициент

1/M

. Из анализа алгоритма (56) следует,

что для его реализации потребуется

+2 ячейки памяти, а время

готовности алгоритма выдать с заданной точностью

1-е сглаженное

значение составит

ск.ср.iопр

t=MT

. (58)

Величина параметра сглаживания

вычисляется по заданному

значению коэффициента ослабления помех

, который, в свою

очередь, представляет собой отношение:

η =

, (59)

где

- дисперсия помех в отсчетах датчиков x

xci

- дисперсия

помех в сглаженных, вычисленных в соответствии с алгоритмом (56)

значениях

Чтобы оценить величину M

, представим каждую из переменных,

входящих в выражения (56), (57) как:

⎫

⎪

⎬

⎪

⎭

ik x ik

x=mo+Δx,

xc = mo + Δxc

(60)

Подставляя (60) в (56) или (57) и вычитая из результата подобные

уравнения, записанные относительно математических ожиданий,

получим уравнения относительно абсолютных значений

погрешностей, которые будут идентичны выражениям (56) и (57)

соответственно, например:

i1 i1 i2 i(M )

Δxc = (Δx+Δx+...+Δx)

Предполагая, что значения погрешностей в соседних точках не

коррелированны и характеризуются дисперсией

можно записать

следующее уравнение относительно дисперсии погрешности

сглаживания:

iiii

2222

xc x x x

σ =×(σ +σ +...+σ )

444

4443

или

134

xc i x

σ =(M×σ )=

Следовательно, с учетом выражения (60) значение параметра

сглаживания для

i–го датчика

=η

.. (61)

2.5.3. Экспоненциальное сглаживание. Для экспоненциального

сглаживания алгоритм имеет вид:

ik i(k-1) i ik i(k-1)

xc = xc + α (x - xc )

(62)

при начальном значении

=0 и диапазоне изменения параметра

сглаживания:

0<α

<1.

Следует отметить, что в реальных условиях в результате вывода

технологического процесса или технического объекта в

установившийся режим работы становится известным желаемое

значение контролируемой или регулируемой переменной, которое

ранее было обозначено как

. Именно эта величина и может быть

использована в качестве начального значения

Величина параметра

α определяет длительность переходных

процессов и качество сглаживания. Чем меньше

α, тем лучше

сглаживание, но тем большее время потребуется для получения

сглаженного значения

с заданным ослаблением помехи η

Поэтому, как и в предыдущем алгоритме сглаживания, возникает

задача нахождения значения параметра сглаживания

и времени

готовности алгоритма (62) вычислить

1-е сглаженное значение xc

принятым коэффициентом ослабления помех

Для определения параметра сглаживания

перейдем в выражении

(62) к дисперсиям погрешностей измерений, принимая те же

допущения, что и для алгоритма (56), тогда

iii

22222

xc i xc i x

σ =(1-α ) σ + ασ

Откуда

1 α

η 2-α

, (63)

или

α =

η +1

(64)

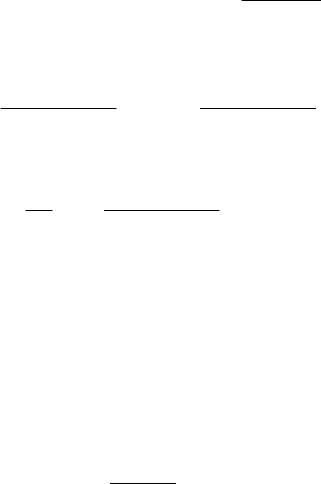
135

Выражение (64) позволяет рассчитать параметр

для алгоритма

экспоненциального сглаживания, если задан коэффициент ослабления

помех

. Алгоритм (62) можно представить не в рекуррентной форме,

а в виде суммы следующего вида:

() () () ()

23 k-1

ik i ik i i(k-1) i i(k-2) i i(k-3) i i1

xc = α[x + 1- α x+1-α x+1-α x +... + 1-α x]

Считая, что погрешности измерения в каждом отсчете

i–го датчика

не коррелированны, приходим к аналогичному уравнению

относительно дисперсий этих погрешностей, т.е.

22 2 2×2 2×3 2×(k-1)2

xci i i i i i x

σ =α {[1+(1- α )+(1-α )+(1-α ) +... +(1-α )]σ }

Выражение в квадратных скобках можно записать как сумму

убывающей геометрической прогрессии

a(1-q )

1-q

со знаменателем

q=(1-α )

Следовательно,

iii

2k 2k

22 2 2

xc i x i x

1-(1-α )1-(1-α )

σ = ασ= ασ

1-(1-α )2-α

. (65)

В результате на основании формул (63) и (65) получаем

11-(1-α )

= α

η 2-α

(66)

В выражении (66) член

(1 - α )

с ростом k стремится к нулю,

приближаясь к (63). Задаваясь степенью приближения

δ, можно

вычислить значение

k, которое будет определять количество

рекуррентных вычислений в алгоритме (62), и, следовательно, время

получения первого сглаженного значения при заданном коэффициенте

ослабления (59).

На основании сказанного из равенства

(1 - α )=δ

находим

⎧

⎫

⎨

⎬

⎩⎭

lnδ

k=E0,5

ln(1- α )

, (67)

откуда ясно, что первое сглаженное значение будет получено с

заданной точностью в соответствии с алгоритмом (62) спустя время

136

⎧⎫

⎨⎬

⎩⎭

экс.сгл i опр опр

lnδ

t = k T = E 0,5T

ln(1 - α )

. (68)

Как следует из (68), это время будет возрастать с увеличением

точности вычислений

δ. Достоинством алгоритма экспоненциального

сглаживания, по сравнению со скользящим окном, является малый

объем памяти, хотя он значительно дольше входит в установившийся

режим.

Выбор того или иного алгоритма зависит от конкретных требований

к быстродействию и объему памяти, сформулированных в ТЗ на

разработку системы.

На рис. 29 приведены графики изменения сигналов, построенные с

помощью

пакета MatLab по результатам работы программ в

соответствии с описанными выше алгоритмами.

В качестве исходного массива данных по

i-му каналу измерения

был использован массив нормально распределенных чисел с

заданными параметрами. На рис. 29.а представлен график этого

массива, но с наложением в произвольных точках импульсных помех,

обрыва и короткого замыкания. После отработки программы

«Проверка на достоверность» был получен массив, представленный на

рис. 29.b. Этот массив затем обрабатывался программами «Скользящее

среднее

» и «Экспоненциальное сглаживание». Задавая различные

значения коэффициента ослабления

, рассчитав параметры

сглаживания

и α

можно было проверить работу предложенных

алгоритмов. В частности, представленные на рис. 29.c и рис. 29.d

графики соответствуют расчетным значениям

η=М=10 и α=0,18. При

этом величина

k=17 при при заданной точности δ=0,001.

137

0 50 100 150 200 250 300 350 400 450 500

Dispersiya:1045.0078

0 50 100 150 200 250 300 350 400 450 500

Dispersiya:0.89051; Korotkoe zamikanie na otschete:310; Obriv v kanale na otschet

0 50 100 150 200 250 300 350 400 450 500

Dispersiya:0.087716; Neksper:10.1522; Tckcp=10*Topr

0 50 100 150 200 250 300 350 400 450 500

Dispersiya:0.087969; Neksper:10.123; Tekssgl=17.2117*Topr

Exponencialnoye sglajivaniye

Sglajivaniye skolzjashim srednim

Signal posle proverki

Signal v kanale izmereniya

Рис. 29

Экспериментальное значение коэффициента ослабления η, как

подтвердило моделирование, получилось равным заданному с

точностью (1.2-1.5)%.

2.5.4. Пересчет в технические единицы. Для представления

оператору-технологу реальных значений технологических переменных

существуют формулы пересчета, вид которых определяется типом

датчиков.

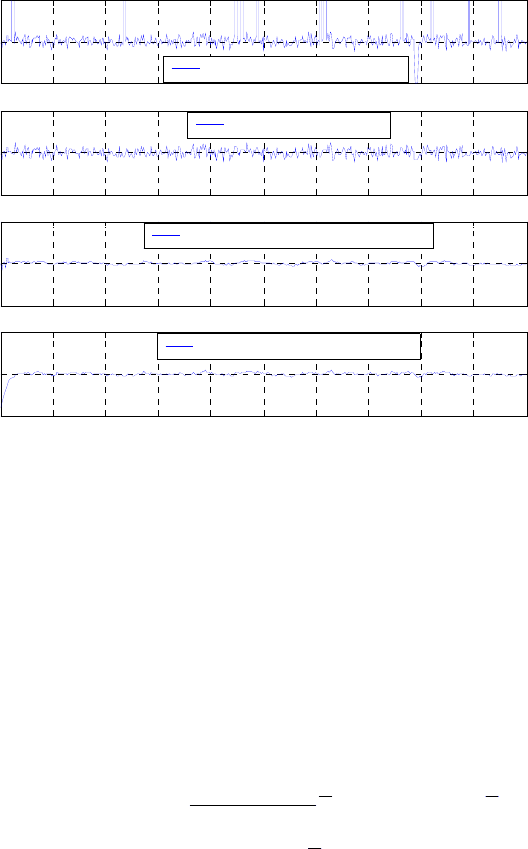
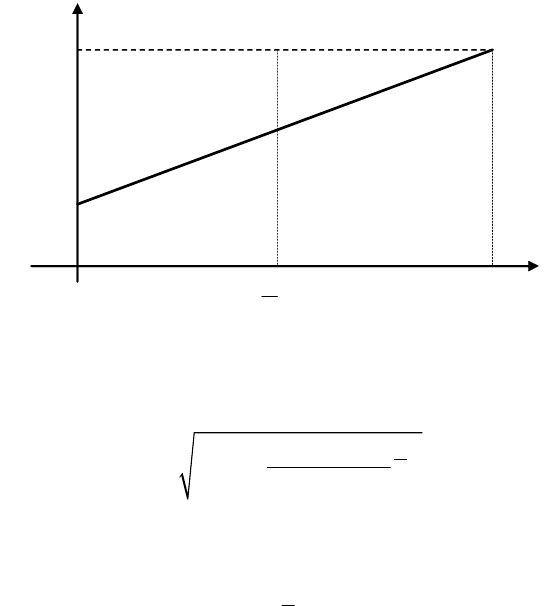
Если у датчика линейная градуировочная характеристика (см.

рис. 30), как например, у датчиков уровня, давления, то пересчет

осуществляется в соответствии со следующим выражением:

iмин iмакс

ik iмин ik iмин прсiik

АЦПi

X-X

x=X+ x=X+kx

2-1

, (69)

в котором черточкой над переменной (

x ) обозначен её цифровой

код, индекс

i относится к номеру канала измерения, индекс k – к

номеру отсчета в этом канале.

138

АЦП

imin

imax

i-k

Рис. 30

При нелинейной характеристике, например, квадратичной пересчет

выполняется по следующей формуле:

iмин iмакс

ik iмин ik

АЦПi

X-X

x=X + x

2-1

. (70)

Подобной характеристикой обладают обычно датчики расхода.

Для многих датчиков градуировочная характеристика предсталяется

в виде степенного ряда

∑

ik j ik

j=0

x= ax, j≤4.. (71)

Например, для датчиков температуры достаточно степень

аппроксимирующего полинома

j брать не более двух.

2.5.5. Проверка на технологические границы. Эта проверка

является одним из основных элементов контроля хода ТП. Контроль

производится путем сравнения текущего значения технологической

переменной

с заданными значениями верхней XB

и нижней XH

границ [56]. При нарушении этих границ программа выдает признак

нарушения

1γ =

, фиксирует время нарушения, сообщает оператору-

технологу о нарушении и посылает все данные в архив.

Чтобы предупредить повторные переключения признака γ

, когда

значение технологической переменной колеблется вблизи одной из

границ, вводится полоса гистерезиса δ

, равная, например, 5% от

139

диапазона изменения этой переменной. В результате признак

нарушения границы вырабатывается в соответствии с условиями:

≥≤

⎫

⎬

≤≤

⎭

ik ik i ik i

ik i i i(k-1) ik i i i(k-1)

g=1 при xXB или xXH,

g=0 при XH + d g x XB - d g

(72)

Подобная проверка предусмотрена и в SCADA-системе TRACE

MODE. Но, помимо зоны гистерезиса, в TRACE MODE предусмотрена

зона предупреждения по предаварийной ситуации.

2.6. Оценка погрешностей программных модулей ПСОИ

Как было отмечено ранее, вычисления в микроконтроллере

сопровождаются погрешностями, которые влияют на точность

результата. Рассмотрим, как оцениваются эти погрешности, и каким

образом их можно уменьшить. Среди погрешностей вычислений

обычно различают три их вида:

- погрешность инструментальная за счет ограниченной длины

разрядной сетки;

- погрешность метода за счет неточной аппроксимации

градуировочной кривой или

за счет приближенных значений интеграла

и производной при использовании формул численного интегрирования

и численного дифференцирования;

- трансформированная погрешность, обусловленная

преобразованием погрешностей во входных переменных с помощью

алгоритма вычислений на его выход.

Каждая процедура первичной обработки может быть реализована

различными вариантами алгоритмов, отличающимися точностью

выполнения операций, временем ее выполнения в МК, объемом

занимаемой памяти и т.д.

Основная задача при построении подсистемы первичной обработки

заключается в определении рационального варианта алгоритма

обработки и выбора аппаратуры с тем, чтобы обеспечить требуемую

точность вычисления контролируемого параметра и время реакции

системы на чрезвычайную ситуацию на объекте.

Вычислительная погрешность, влияющая на точность

представления

i-го контролируемого параметра на выходе подсистемы

первичной обработки информации, определяется как

222

кнтрi окрi трфi

σ = σ + σ , (73)

140

где

окрi

σ - дисперсия погрешности округления или, как её еще

называют, инструментальной погрешности,

трфi

- дисперсия

трансформированной погрешности.

2.6.1. Инструментальная погрешность. Величина разрядной сетки

влияет на точность контролируемых и управляемых переменных, а

также на стоимость микроконтроллера. Поэтому, как уже отмечалось,

одним из критериев выбора МК является обеспечение заданной

точности, по возможности, минимальной длиной разрядной сетки.

Длина разрядной сетки непосредственно влияет на инструментальную

погрешность или погрешность округления. Кроме того, на величину

этой погрешности

будет влиять количество последовательных

округлений в алгоритме вычислений.

Для примера оценим инструментальную погрешность при

вычислении произведения двух чисел:

П=а×ε. В результате округления

каждый множитель этого произведения представлен в МК целым

числом квантов Δ

a и Δε, т.е.

a=PΔa, ε =NΔε .

С учетом процедуры округления для каждого множителя

a=a+β ,

ε = ε + β . и результата произведения

ПεaaεП

П = П + β =aε +aβ + εβ + ββ + β ,

где β

, β

- погрешности округления соответственно множителей и

результата их перемножения, имеющие дисперсии

222 2

a εПокр

σ = σ = σ = σ , получим следующее выражение для дисперсии

погрешности округления произведения:

2222

Покр

σ ={a +ε }σ .

При вычислениях с фиксированной запятой, исходные данные

должны быть масштабированы так, чтобы и множители и результат

умножения были близки к единице, т.е. чтобы не было потери в

точности вычисления. Тогда, если

a, ε близки к единице, то

≅

АЛУ

Покр

σ 3σ =3

где Δ

АЛУ

- величина младшего разряда операционного устройства.

Из анализа полученных результатов можно сделать вывод, что

суммарная погрешность округления в МК складывается из