Powers D.L. Boundary Value Problems and Partial Differential Equations
Подождите немного. Документ загружается.

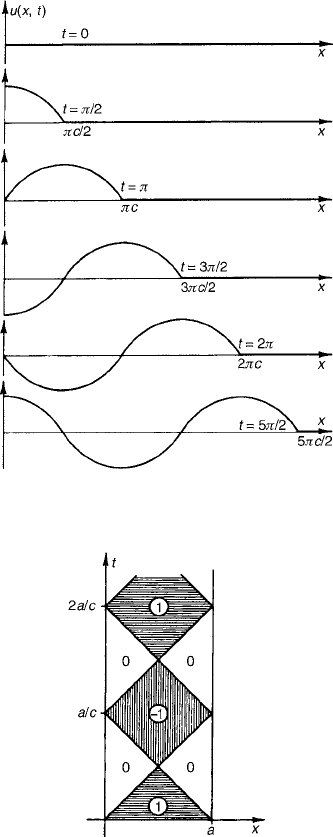
468 Answers to Odd-Numbered Exercises
Figure 5 Solution for Exercise 5, Section 3.6.
Figure 6 Solution of Miscellaneous Exercise 3, Chapter 3.
3. See Fig. 6.
5. See Fig. 7.
7. See Fig. 8.
9. See Fig. 9.
11. See Fig. 10.

Chapter 3 469
Figure 7 Solution of Miscellaneous Exercise 5, Chapter 3.
Figure 8 Solution of Miscellaneous Exercise 7, Chapter 3.
13. See Fig. 11.
15. Using y(x) = x(1 −x),findλ
2
1
≤10.5.
17. f (q) = 12a
2
sech
2
(aq), c = 4a
2
.
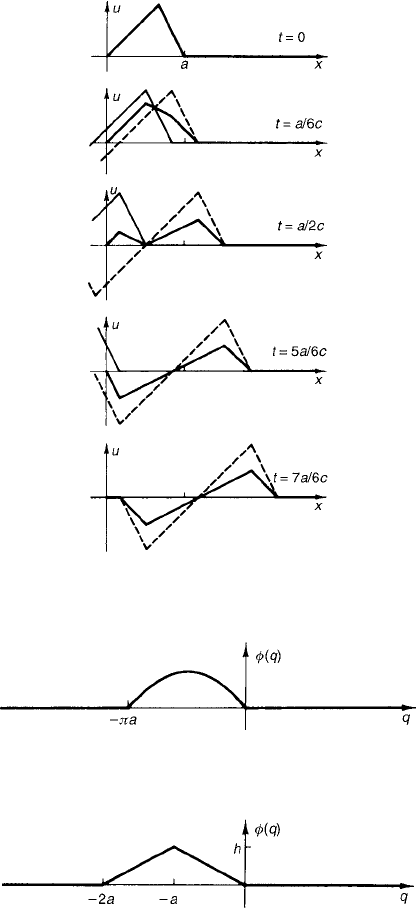
470 Answers to Odd-Numbered Exercises
Figure 9 Solution of Miscellaneous Exercise 7, Chapter 3.
Figure 10 Solution for Miscellaneous Exercise 11, Chapter 3.
Figure 11 Solution of Miscellaneous Exercise 13, Chapter 3.
21. v(x, t) =
∞
n=1
a
n
cos(λ
n
ct) + b
n
sin(λ
n
ct)
sin(λ
n
x),
λ
n
=(2n −1)π/2a,

Chapter 4 471
a
n
=
8aU
0
(−1)
n+1
π
2
(2n −1)
2
, b
n
=0.
23.
Y
Y
=
2V
k
ψ
ψ
.Thefunctionφ(x −Vt) cancels from both sides.
25. φ
n
(−Vt) = T
0
exp(λ
2
n
kt/2)b
n
, t > 0,
φ
n
(x) = T
1
exp(λ
2
n
kx/2V)b
n
, x > 0,
where
∞
n=1
b
n
sin(λ
n
y) = 1, 0 < y < b.
27. φ(x − ct) = e
−c(x−ct)/k
= e
(c
2
t−cx)/k
.Thegivenc satisfies c
2
= iωk,
so φ(x − ct) = e
iωt−(1+i)px
= e
−px
e
i(ωt−px)
. Now form
1
2
(φ(x − ct) +
φ(x − ct)) = e
−px
cos(ωt − px) and so forth.
29. Differentiate and substitute.
31. φ
(2)
−φ
(4)
+λ
2
φ = 0,
φ(0) = 0, φ(a) = 0,
φ
(0) =0, φ
(a) =0.
33. λ
n
=
nπ
a
1 +
nπ
a
2
∼
=
nπ
a
.
Chapter 4
Section 4.1
1. f +d =0.
3. Y(y) = A sinh(πy), A = 1/ sinh(π).
5. v(r) = a ln(r) +b.
7.
∂u
∂x
=
∂v
∂r
cos(θ) −
∂v
∂θ
sin(θ)
r
,
∂u
∂y
=
∂v
∂r
sin(θ) +
∂v
∂θ
cos(θ)
r
.
9. a.
∂
2
u
∂x
2
+
∂
2
u
∂y
2
=0, 0 < x < a,0< y < b,
u(0, y) = 0, u(a, y) = 0, 0 < y < b,
u(x, 0) = f (x), u(x, b) = f (x),0< x < a.
472 Answers to Odd-Numbered Exercises
Membrane is attached to a frame that is flat on the left and right but has
the shape of the graph of f (x) at top and bottom.
b.
∂
2
u
∂x
2
+
∂
2
u
∂y
2
=0, 0 < x < a,0< y < b,
∂u
∂x
(0, y) =0, u(a, y) = 0, 0 < y < b,
u(x, 0) = 0, u(x, b) = 100, 0 < x < a.
The bar is insulated on the left; the temperature is fixed at 100 on the top,
at 0 on the other two sides.
c.
∂
2
u
∂x
2
+
∂
2
u
∂y
2
=0, 0 < x < a,0< y < b,
u(0, y) = 0, u(a, y) = 100, 0 < y < b,
∂u
∂y
(x, 0) = 0,
∂u
∂y
(x, b) = 0, 0 < x < a.
The sheet is electrically insulated at top and bottom. The voltage is fixed
at 0 on the left and 100 on the right.
d.
∂
2
φ
∂x
2
+
∂
2
φ
∂y
2
=0, 0 < x < a,0< y < b,
∂φ
∂x
(0, y) = 0,
∂φ
∂x
(a, y) =−a,0< y < b,
∂φ
∂y
(x, 0) = 0,
∂φ
∂y
(x, b) = b,0< x < a.
The velocities, given by V =−∇φ,areV
x
= a, V
y
= 0ontheright,
V
x
=0, V
y
=−b onthetop;andwallsontheothertwosidesmakeve-
locities 0 there.
Section 4.2
1. Show by differentiating and substituting that both are solutions of the
differential equation. The Wronskian of the two functions is
sinh(λy) sinh(λ(b −y))
λ cosh(λy) −λ cosh(λ(b −y))
=−λ sinh(λb) = 0.
3. In the case b = a , use two terms of the series: u(a/2, a/2) = 0.32.
5. u(x, y) =
∞
1
b
n
sin
nπx
a
sinh(nπy/a)
sinh(nπb/a)
, b
n
=
8
n
2
π
2
sin
nπ
2
.

Chapter 4 473
7. a. See Eq. (11). a
n
=0, c
n
=200(1 −cos(nπ ))/nπ ;
b. u(x, y) = u
1
(x, y) + u
2
(x, y), u
1
(x, y) is the solution to Part a,
u
2
(x, y) =
∞
n=1
c
n
sinh(µ
n
x)
sinh(µ
n
a)
sin(µ
n
y),
µ
n
=nπ/b, c
n
=200(1 −cos(nπ ))/nπ .
c. u(x, y) = u
1
(x, y) + u
2
(x, y),where
u
1
(x, y) =
∞
n=1
c
n
sinh(λ
n
y)
sinh(λ
n
b)
sin(λ
n
x),
u
2
(x, y) =
∞
n=1
c
n
sinh(µ
n
x)
sinh(µ
n
a)
sin(µ
n
y).
In both series, c
n
=2ab(−1)
n+1
/nπ. Also note u(x, y) = xy.
Section 4.3
1. a. u(x, y) = 1, but the form found by applying the methods of this sec-
tion is
u(x, y) =
∞
n=1
a
n
sinh(λ
n
y) +sinh(λ
n
(b −y))
sinh(λ
n
b)
cos(λ
n
x)
+
∞
n=1
b
n
cosh(µ
n
x)
cosh(µ
n
a)
sin(µ
n
y),
where
λ
n
=
(2n −1)π
2a
, a
n
=
4sin
(2n−1)π
2
π(2n −1)
,
µ
n
=
nπ
b
, b
n
=
2(1 −cos(nπ))
nπ
.
b. u(x, y) = y/b, and this is found by the methods of this section. In this
case, 0 is an eigenvalue.
c.
4
π
∞
1
(−1)
n+1
cos(λ
n
y)
(2n −1)
sinh(λ
n
(a −x))
sinh(λ
n
a)
, λ
n
=
2n −1
2
π
b
.
3. b
0
b =
V
0
2
, b
n
sinh(λ
n
b) =
2V
0
(cos(nπ)−1)
n
2
π
2
.

474 Answers to Odd-Numbered Exercises
5. Check zero boundary conditions by substituting. At x = a,find
A
n
cosh(µ
n
a) =
2
b
b
0
Sy cos(µ
n
y)dy.
7. w(x, y) =
∞
n=1
a
n
cosh(λ
n
y) cos(λ
n
x). From the condition at y = b,
a
n
cosh(λ
n
b) =
2
a
a
0
Sb
a
(x −a) cos(λ
n
x)dx.
9. w(x, y) =
∞
n=1
c
n
sinh(λ
n
y) +a
n
sinh(λ
n
(b −y))
sinh(λ
n
b)
sin(λ
n
x),
a
n
=c
n
=−
2
a
a
0
Hx(a −x) sin(λ
n
x)dx =−2Ha
2
1 −cos(nπ)
n
3
π
3
.
11. 12A + 2C =−K,12E + 2C =−K. There are many solutions.
Section 4.4
1. a
n
=
2
a
a
0
f (x ) sin
nπx
a
dx .
3. A(µ) =
2
π
∞
0
g
2
(y) sin(µy)dy.
5. a. u(x, y) =
c
n
cos(λ
n
x) exp(−λ
n
y), λ
n
=(2n −1)π/2a,
c
n
=4(−1)
n+1
/π(2n −1);
b. u(x, y) =
∞
0
B(λ) cosh(λx) sin(λy)dλ, B(λ) =
2λ
π(λ
2
+1) cosh(λa)
;
c. u(x, y) =
∞
0
A(λ) cos(λy) sinh(λx)dλ, A(λ) =
2sin(λb)
πλsinh(λa)
.
7. u(x, y) =
∞
1
b
n
sin(λ
n
x) exp(−λ
n
y)
+
∞
0
A(µ)
sinh(µx)
sinh(µa)
+B(µ)
sinh(µ(a − x))
sinh(µa)
sin(µy)dµ,
λ
n
=nπ/a, b
n
=2(1 −cos(nπ ))/nπ , A(µ) = B(µ) = 2µ/π(µ
2
+1).
Also see Exercise 8.
9. a. u(x, y) =
2
π
∞
0
1 −cos(λa)
λ
sin(λx)
sinh(λy)
sinh(λb)
dλ;

Chapter 4 475
b. u(x, y) =
2
π
∞
0
λ
1 +λ
2
sin(λx)
sinh(λ(b −y))
sinh(λb)
dλ.
11. u(x, y) =
∞
0
2
π(1 +λ
2
)
sinh(λx)
sinh(λa)
cos(λy)dλ.
13. e
−λy
sin(λx), λ>0.
15. e
−λy
sin(λx), e
−λy
cos(λx), λ>0.
17. u(x, y) =
1
π
π
2
+tan
−1
(x/y)
.
19. This solution is unbounded as x tends to infinity and cannot be found
by the method of this section.
Section 4.5
1. v(r,θ) is given by Eq. (10) with b
n
=0, a
0
=π/2,
a
n
=−2(1− cos(nπ))/π n
2
c
n
.
3. The solution is as in Eq. (10) with b
n
=0, a
0
=1/π , a
1
=1/2, and
a
n
=
2sin((n −1)π/2)
π(n
2
−1)
for n = 1.
5. Convergence is uniform in θ .
7. a
0
=
1
2π
π
−π
f (θ)dθ , a
n
=
c
n
π
π
−π
f (θ) cos(nθ)dθ ,
b
n
=
c
n
π
π
−π
f (θ) sin(nθ)dθ.
9.
2
π
∞
n=1
1 −cos(nπ)
nc
2n
r
2n
sin(2nθ)= v(r,θ).
11. v
n
(r,θ)= r
n/α
sin(nθ/α) has ∂v/∂r unbounded as r → 0+,ifn = 1.
Section 4.6
1. Hyperbolic (a) and (e); elliptic (b) and (c); parabolic (d).
3. Only (e).
5. a. u(x, y) =
∞
1
a
n
sin(nπx)e
−nπy
;
b. u(x, y) =
∞
1
a
n
sin(nπx) cos(nπy);
476 Answers to Odd-Numbered Exercises
c. u(x, y) =
∞
1
a
n
sin(nπx) exp(−n
2
π
2
y),
a
n
=2
1
0
f (x) sin(nπx)dx.
7. X
/X =−λ
2
, T
/T =−λ
2
/(1 +λ
2
).
Chapter 4 Miscellaneous Exercises
1. u(x, y) =
∞
1
b
n
sinh(λ
n
(a −x))
sinh(λ
n
a)
sin(λ
n
y),
λ
n
=nπ/b, b
n
=2(1 −cos(nπ ))/nπ .
3. u(x, y) = 1.Notethat0isaneigenvalue.
5. u(x, y) =
∞
n=1
a
n
sinh(λ
n
x) + b
n
sinh(λ
n
(a −x))
sinh(λ
n
a)
cos(λ
n
y),
λ
n
=(2n −1)π/2b, a
n
=b
n
=4(−1)
n+1
/π(2n − 1).
7. u(x, y) = w(x, y) +w(y, x),where
w(x, y) =
∞
n=1
b
n
sinh(λ
n
(a −y))
sinh(λ
n
a)
sin(λ
n
x),
λ
n
=nπ/a, b
n
=
8h
n
2
π
2
sin
nπ
2
.
9. u(x, y) =
∞
0
A(λ)
sinh(λ(b −y))
sinh(λb)
cos(λx)dλ, A(λ) = 2sin(λa)/λπ.
11. u(x, y) =
∞
0
A(λ) cos(λx )e
−λy
dλ, A(λ) = 2α/π
α
2
+λ
2
.
13. u(x, y) =
−1
π
tan
−1
x −x
y
∞
−∞
=
1
π
π
2
−
−
π
2
.
15. u(r,θ)=a
0
+
∞
n=1
r
c
n
a
n
cos(nθ)+b
n
sin(nθ)
,
a
0
=
1
2
, a
n
=0, b
n
=
1 −cos(nπ)
nπ
.
17. Same form as Exercise 15, but a
0
=2/π ,
a
n
=2(1 +cos(nπ ))/(1 −n
2
), b
n
=0(anda
1
=0).
19. u(r,θ)=(ln(r) −ln(b))/(ln(a) −ln(b)).

Chapter 4 477
21. u(r,θ)=
∞
1
b
n
r
c
n/2
sin(nθ/2), b
n
=
1
π
2π
0
f (θ) sin(nθ/2)dθ .
23. u(x, y) =
c
n
sinh(λ
n
y) sin(λ
n
x), λ
n
=(2n −1)π/2a,
c
n
=2sin(λ
n
a)/(aλ
2
n
sinh(λ
n
b)).
25. w satisfies the potential equation in the rectangle with boundary condi-
tions
w(0, y) = 0, w
x
(a, y) = ay/b,0< y < b,
w(x, 0) = 0, w(x, b) = 0, 0 < x < a.
w(x, y) =
∞
n=1
b
n
sin(λ
n
y) cosh(λ
n
x),
λ
n
=nπ/b, b
n
=2a(−1)
n+1
/n
2
π
2
cosh(λ
n
a).
27. The equations become
∂
2
φ
∂y∂x
=
∂
2
φ
∂x∂y
,
1 −M
2
∂
2
φ
∂x
2
+
∂
2
φ
∂y
2
=0.
29. φ(x, y) =
∞
0
A(α) cos(αx) + B(α) sin(αx)
e
−βy
dα +c,
where β = α
√
1 −M
2
, c is an arbitrary constant, and
A(α)
B(α)
=−
U
0
βπ
∞
−∞
f
(x)
cos(αx)
sin(αx)
dx.
31. If (x(s), y(s)) is the parametric representation for the boundary curve
C,
then the vector y
i −x
j is normal to C,and
C
∂u
∂n
ds =
C
∂u
∂x
dy −
∂u
∂y
dx.
By Green’s theorem,
C
∂u
∂x
dy −
∂u
∂y
dx =
R
∂
2
u
∂x
2
+
∂
2
u
∂y
2
dA,
which is 0, since u satisfies the potential equation in
R.
33. Substitute directly.
35. −∇u =−(xi +yj)/(x
2
+y
2
).
