Powers D.L. Boundary Value Problems and Partial Differential Equations
Подождите немного. Документ загружается.

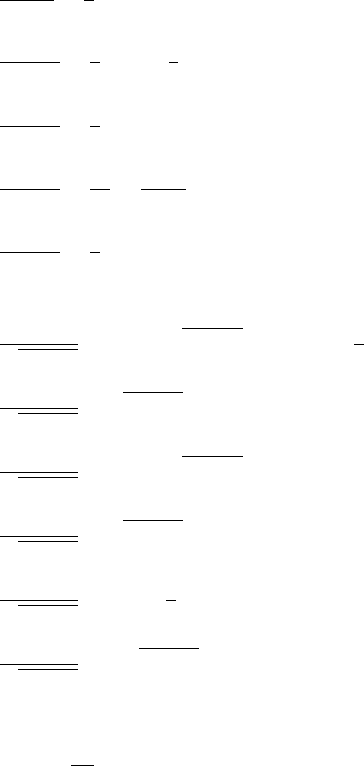
438 Appendix: Mathematical References
e. Integrated Bessel function
IJ(x) =
x
0
J
0
(z) dz
Table of Integrals
Any letter except x represents a constant. The integration constants have been
left off.
1. Rational functions
1.1
dx
h +kx
=
1
k
ln |h + kx|
1.2
dx
x
2
+a
2
=
1
a
tan
−1
x
a
1.3
xdx
x
2
+a
2
=
1
2
ln
x
2
+a
2
1.4
dx
x
2
−a
2
=
1
2a
ln
x −a
x +a
1.5
xdx
x
2
−a
2
=
1
2
ln
x
2
−a
2
2. Radicals
2.1
dx
√
x
2
+a
2
=ln
x +
x
2
+a
2
or sinh
−1
x
a
2.2
xdx
√
x
2
+a
2
=
x
2
+a
2
2.3
dx
√
x
2
−a
2
=ln
x +
x
2
−a
2
(x > a)
2.4
xdx
√
x
2
−a
2
=
x
2
−a
2
2.5
dx
√
a
2
−x
2
=sin
−1
x
a
(|x | < a)
2.6
xdx
√
a
2
−x
2
=−
a
2
−x
2
(|x | < a)
3. Exponentials and hyperbolic functions
3.1
e
kx
dx =
e
kx
k
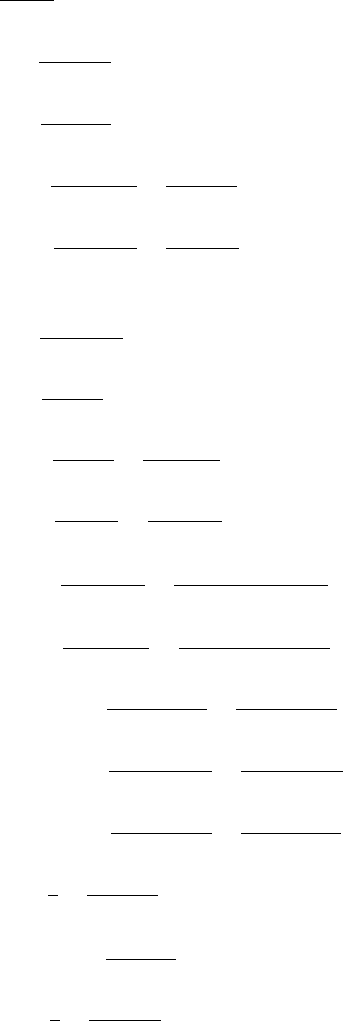
Appendix: Mathematical References 439
3.2
xe
kx
dx =
kx − 1
k
2
e
kx
3.3
sinh(kx) dx =
cosh(kx)
k
3.4
cosh(kx) dx =
sinh(kx)
k
3.5
x sinh(kx) dx =
x cosh(kx)
k
−
sinh(kx)
k
2
3.6
x cosh(kx) dx =
x sinh(kx)
k
−
cosh(kx)
k
2
4. Sines and cosines
4.1
sin(λx) dx =
−cos(λx )
λ
4.2
cos(λx) dx =
sin(λx)
λ
4.3
x sin(λx) dx =
sin(λx)
λ
2
−
x cos(λx)
λ
4.4
x cos(λx) dx =
cos(λx)
λ
2
+
x sin(λx)
λ
4.5
x
2
sin(λx) dx =
2x sin(λx)
λ
2
+
(2 −λ
2
x
2
) cos(λx )
λ
3
4.6
x
2
cos(λx) dx =
2x cos(λx)
λ
2
+
(λ
2
x
2
−2) sin(λx)
λ
3
4.7
sin(λx) sin(µx) dx =
sin(µ −λ)x
2(µ −λ)
−
sin(µ +λ)x
2(µ +λ)
(λ = µ)
4.8
sin(λx) cos(µx) dx =
cos(µ −λ)x
2(µ −λ)
−
cos(µ +λ)x
2(µ +λ)
(λ =µ)
4.9
cos(λx) cos(µx) dx =
sin(µ −λ)x
2(µ −λ)
+
sin(µ +λ)x
2(µ +λ)
(λ = µ)
4.10
sin
2
(λx) dx =
x
2
−
sin(2λx)
4λ
4.11
sin(λx) cos(λx) dx =
sin
2
(λx)
2λ
4.12
cos
2
(λx) dx =
x
2
+
sin(2λx)
4λ
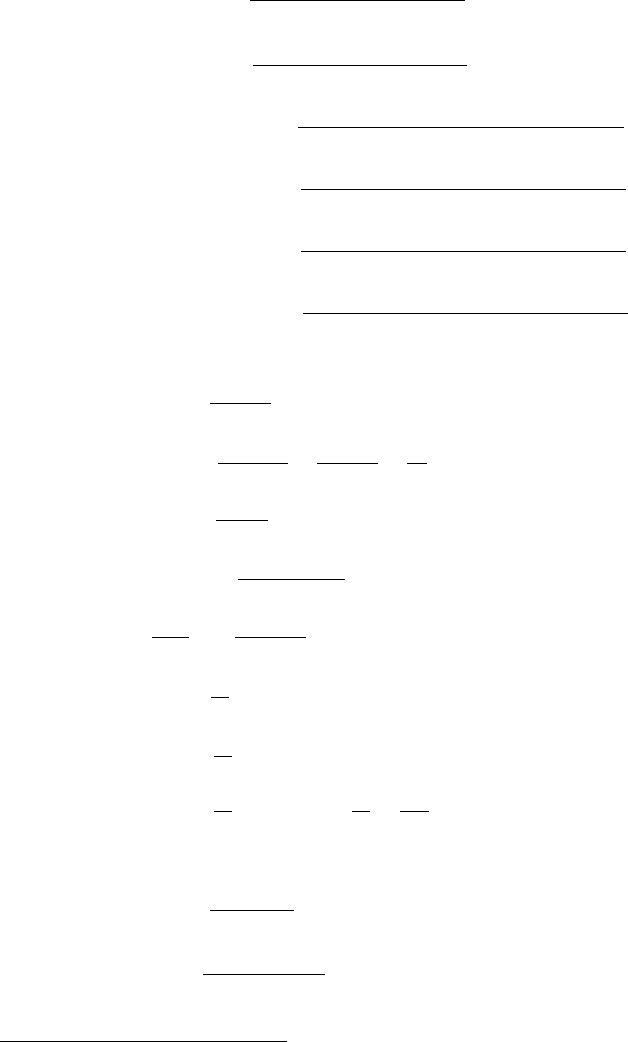
440 Appendix: Mathematical References
4.13
e
kx
sin(λx) dx =
e
kx
(k sin(λx) −λ cos(λx))
k
2
+λ
2
4.14
e
kx
cos(λx) dx =
e
kx
(k cos(λx) +λ sin(λx))
k
2
+λ
2
4.15
sinh(kx) sin(λx) dx =
k cosh(kx) sin(λx) −λ sinh(kx) cos(λx)
k
2
+λ
2
4.16
sinh(kx) cos(λx) dx =
k cosh(kx) cos(λx) + λ sinh(kx) sin(λx)
k
2
+λ
2
4.17
cosh(kx) sin(λx) dx =
k sinh(kx) sin(λx) −λ cosh(kx) cos(λx)
k
2
+λ
2
4.18
cosh(kx) cos(λx) dx =
k sinh(kx) cos(λx) +λ cosh(kx) sin(λx)
k
2
+λ
2
5. Bessel functions
5.1
xJ
0
(λx) dx =
xJ
1
(λx)
λ
5.2
x
2
J
0
(λx) dx =
x
2
J
1
(λx)
λ
+
xJ
0
(λx)
λ
2
−
1
λ
3
IJ(λx)
1
5.3
J
1
(λx) dx =−
J
0
(λx)
λ
5.4
x
n+1
J
n
(λx) dx =
x
n+1
J
n+1
(λx)
λ
5.5
J
n
(λx)
dx
x
n−1
=−
J
n−1
(λx)
λx
n−1
5.6
J
2
0
(λx)xdx=
x
2
2
J
2
0
(λx) + J
2
1
(λx)
5.7
J
2
n
(λx)xdx=
x
2
2
J
2
n
(λx) − J
n−1
(λx)J
n+1
(λx)
=
x
2
2
J
n
(λx)
2
+
x
2
2
−
n
2
2λ
2
J
n
(λx)
2
6. Legendre polynomials
6.1
P
n
(x) dx =−
−(1 −x
2
)
n(n +1)
P
n
(x)
6.2
xP
n
(x) dx =
(1 −x
2
)
(n +2)(n −1)
P
n
(x) −xP
n
(x)
.
1
See Calculus 5e.

Answers to
Odd-Numbered
Exercises
Chapter 0
Section 0.1
1. φ(x) = c
1
cos(λx) +c
2
sin(λx).
3. The equation has constant coefficients k = 0, p = 0; u(t) = c
1
+c
2
t.
5. w(r) =c
1
r
λ
+c
2
r
−λ
.
7. Integrate, solve for dv/dx, and integrate again:
v(x) = c
1
+c
2
ln |h +kx|.
9. u(x) =c
1
+c
2
/x
2
.
11. u(r) = c
1
+c
2
ln(r).
13. Characteristic polynomial m
4
−λ
4
=0; roots m =±λ, ±iλ. General so-
lution u(x) = c
1
cos(λx) + c
2
sin(λx) +c
3
cosh(λx) +c
4
sinh(λx).
15. Characteristic polynomial (m
2
+ λ
2
)
2
= 0; roots m =±iλ (double).
General solution u(x) = (c
1
+c
2
x) cos(λx) +(c
3
+c
4
x) sin(λx).
17. v(t) = ln(t) and u
2
(t) = t
b
ln(t).
19. u
+λ
2
u =0; R(ρ) = (a cos(λρ) +b sin(λρ))/ρ.
21. t
2
d
2
u/dt
2
= v
− v
; tdu/dt = v
; v
+ (k − 1)v
+ pv = 0 (constant
coefficients).
441
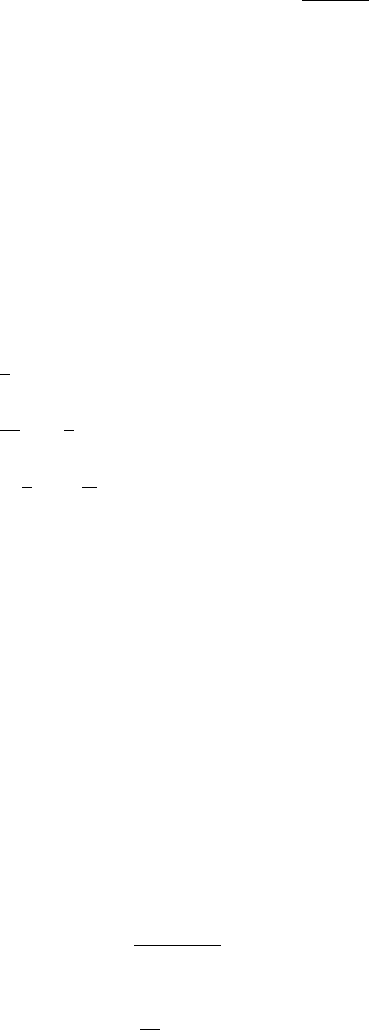
442 Answers to Odd-Numbered Exercises
23. Roots of characteristic equation:
m =−α ±iβ, β =
σ
2
−α
2
.
Solution of differential equation:
y(t) = e
−αt
c
1
cos(βt) +c
2
sin(βt)
.
Initial conditions give: c
1
=−0.001h, c
2
=(α/β)c
1
.
25. v =2.62 m/s.
Section 0.2
1. u(t) = T +ce
−at
.
3. u(t) = te
−at
+ce
−at
.
5. u(t) =
1
2
t sin(t) +c
1
cos(t) + c
2
sin(t).
7. u(t) =
1
12
e
t
+
1
2
te
−t
+c
1
e
−t
+c
2
e
−2t
.
9. u(ρ) =−
1
6
ρ
2
+
c
1
ρ
+c
2
.
11. h(t) =−320t +c
1
+c
2
e
−0.1t
, c
1
=h
0
+3200, c
2
=−3200.
13. v(t) = t, u
p
(t) = te
−at
.
15. v
1
(x) = sin(x) −ln |sec(x) + tan(x)|, v
2
=−cos(x);
u
p
(x) =−cos(x) ln |sec(x) +tan(x)|.
17. v
1
(t) = t
2
/2, v
2
(t) =−t; u
p
(t) =−t
2
/2.
19. v
1
(t) =−1/2t, v
2
(t) =−t/2, u
p
(t) =−1.
23. β = 1/α, K =Rα/ρc.
25. T = β(exp(KI
2
max
(1 −e
−2λt
)/2λ) −1).
Section 0.3
1. a. u(x) = c
2
sin(x), c
2
arbitrary;
b. u(x) =1 −cos(x) −
1 −cos(1)
sin(1)
sin(x) (unique);
c. No solution exists.
3. a. and b. λ =±(2n − 1)
π
2a
, n = 1, 2,...;
Answers to Odd-Numbered Exercises 443
c. λ =±
nπ
a
, n = 0, 1, 2,....
5. c =−a/2, c
=h −
1
µ
cosh
µa
2
.
7. u(x) =T +c
1
cosh(γ x) +c
2
sinh(γ x),where
γ =
hC
κA
and c
1
=T
0
−T, c
2
=−
κγ sinh(γ a) +h cosh(γ a)
κγ cosh(γ a) +h sinh(γ a)
c
1
.
9. u(x) =T +H
1 −cosh(γ x) −
1 −cosh(γ a)
sinh(γ a)
sinh(γ x)
,
where H =
I
2
R
hC
and γ =
hC
κA
.
11. u(y) = y(L −y)g/2µ.
13. P = EI(nπ/L)
2
, n = 1, 2,....
15. u(x) =T +A
1 −cosh(γ x) −
1 −cosh(γ a)
sinh(γ a)
sinh(γ x)
,
A =g/κγ
2
,andγ =
hC
κA
.
17. u(r) = c
1
ln(r/a) + c
2
, c
1
= h
0
h
1
(T
a
− T
W
)/D, c
2
= [h
0
(κ/b +
h
1
ln(b/a))T
W
+(κ/a)h
1
T
a
]/D, D = h
1
κ/a +h
0
κ/b +h
0
h
1
ln(b/a).
19. u(x) =
w
0
EI
x
4
24
−
ax
3
6
+
a
2
x
2
2
.
Section 0.4
1. a. u
+
1
r
u
−u = 0, r =0;
b. u
−
2x
1 −x
2
u
=0, x =±1;
c. u
+cot(φ)u
−u = 0, φ = 0, ±π,±2π,...;
d. u
+
2
ρ
u
+λ
2
u =0, ρ = 0.
3. u(0) bounded; u(ρ) =
H
6κ
c
2
−ρ
2
+
Hc
3h
+T.
5. u(ρ) =
1
ρ
c
1
cos(µρ) +c
2
sin(µρ)
,
u(ρ) ≡ 0unlessµa = π,2π,.... The critical radius is a =
π
µ
.
444 Answers to Odd-Numbered Exercises
7. u(r) = 325 +10
4
(0.25 −r
2
)/4; u(0) = 950.
9. u(x) = T
0
+AL
2
(1 −e
−x/L
).
Section 0.5
1. G(x, z) =
z(a − x)/(−a), 0 < z ≤ x,
x(a −z)/(−a), x ≤ z < a.
3. G(x, z) =
cosh(γ z) sinh(γ (a −x))/(−γ cosh(γ a)), 0 < z ≤x,
cosh(γ x) sinh(γ (a −z))/(−γ cosh(γ a)), x ≤z < a.
5. G(ρ, z) =
(c −ρ)/ρ
−c/z
2
, 0 ≤z <ρ,
(c −z)/z
−c/z
2
,ρ≤z < c.
7. G(x, z) =
sinh(γ z)e
−γ x
−γ
, 0 < z ≤x,
sinh(γ x)e
−γ z
−γ
, x ≤z.
9. u(ρ) = (ρ
2
−c
2
)/6.
11. u(x) =
a
0
G(x, z)f (z)dz =
x
0
z(a − x)
−a
f (z)dz +
a
x
x(a −z)
−a
f (z)dz.
There are two cases:
(i) x ≤ a/2, so u(x) =
a
a/2
x(a −z)
−a
dz;
and
(ii) x > a/2, so u(x) =
a
x
x(a −z)
−a
dz.
Results: u(x) =
−ax/8, 0 < x < a/2,
−x(a −x )
2
/2a, a/2 < x < a.
13. (i) At the left boundary, x = l < z, so the second line of Eq. (17) holds.
The boundary condition (2) is satisfied by v because it is satisfied by u
1
.
At the right boundary, use the first line of Eq. (17).
(ii) At x =z,bothlinesofEq.(17)givethesamevalue.
(iii) v
(z +h) −v
(z −h) =
u
1
(z)u
2
(z +h) −u
1
(z −h)u
2
(z)
W(z)
.
As h approaches 0, the numerator approaches W(z).

Answers to Odd-Numbered Exercises 445
(iv) This is true because u
1
(x) and u
2
(x) are solutions of the homoge-
neous equation.
Chapter 0 Miscellaneous Exercises
1. u(x) =T
0
cosh(γ x) +
T
1
−T
0
cosh(γ a)
sinh(γ x)
sinh(γ a)
.
3. u(x) =T
0
.
5. u(r) = p(a
2
−r
2
)/4.
7. u(ρ) = H(a
2
−ρ
2
)/6 +T
0
.
9. u(x) =T +(T
1
−T) cosh(γ x)/ cosh(γ a).
11. u(x) =T
0
+(T −T
0
)e
−γ x
.
13. h(x) =
ex(a − x) +h
2
0
+(h
2
1
−h
2
0
)(x/a).
15. u(x) =w(1 −e
−γ x
cos(γ x))EI/k,whereγ = (k/4EI)
1/4
.
17. u(x) =
T
0
+Ax, 0 < x <αa,
T
1
−B(a − x), αa < x < a,
A =
κ
2
κ
1
(1 −α) + κ
2
α
T
1
−T
0
a
, B =
κ
1
κ
2
A.
19. u(x) =
1
2
1 −e
−2x
−
1
2
1 −e
−2a
1 −e
−x
1 −e
−a
.
21. a. u(x) = sinh(px)/ sinh(pa);
b. u(x) = cosh(px) −
cosh(pa)
sinh(pa)
sinh(px) = sinh
p(a −x)
/ sinh(pa);
c. u(x) = cosh(px)/ cosh(pa);
d. u(x) = cosh(p(a −x))/ cosh(pa);
e. u(x ) =−cosh(p(a −x))/p sinh(pa);
f. u(x) = cosh(px)/p sinh(pa).
23. u(x) =
x
2
ln
1 +x
1 −x
−1.
25. Multiply by u
and integrate:
1
2
(u
)
2
=
1
5
γ
2
u
5
+ c
1
.Sinceu(x) → 0
as x →∞,alsou
(x) → 0; thus c
1
= 0. Now u
=−
2γ
2
/5u
5/2
or
u
−5/2
u
=−
2γ
2
/5(thenegativerootmakesu decrease) can be in-
tegrated to result in (−2/3)u
−3/2
=−
2γ
2
/5x + c
2
. The condition at
x = 0givesc
2
=(−3/2)U
−3/2
.
446 Answers to Odd-Numbered Exercises
Finally u(x) = (U
−3/2
+(3/2)
2γ
2
/5x)
−2/3
.
27. 459.77 rad/s.
29. u(x) = C
0
e
−ax
.
31. w(x) =
P
2γ
2
1
4
−x
2
+
cosh(γ x) −cosh(γ/2)
γ sinh(γ/2)
.
33. Thesolutionbreaksdown(bucklingoccurs)iftan(λ/2) = γ/2.
Chapter 1
Section 1.1
1. a. 2
sin(x) −
1
2
sin(2x) +
1
3
sin(3x) −···
;
b.
π
2
−
4
π
cos(x) +
1
9
cos(3x) +
1
25
cos(5x) +···
;
c.
1
2
+
2
π
sin(x) +
1
3
sin(3x) +
1
5
sin(5x) +···
;
d.
2
π
−
4
π
1
3
cos(2x) +
1
15
cos(4x) +
1
35
cos(6x) +···
.
3. f (x + p) = 1 =f (x) for any p and all x.
5. If c is a multiple of p,thegraphoff (x) between c and c + p is the same
as that between 0 and p.Otherwise,letk be the integer such that kp lies
between c and c +p:
c+p
c
f (x)dx =
kp
c
f (x )dx +
c+p
kp
f (x)dx =
p
c
∗
f (x)dx +
c
∗
0
f (x)dx,
where c
∗
=c −(k −1)p.
7. a. cos
2
(x) =
1
2
+
1
2
cos(2x);
b. sin
x −
π
6
=cos
π
6
sin(x) − sin
π
6
cos(x);
c. sin(x) cos(2x) =−
1
2
sin(x) +
1
2
sin(3x).
Section 1.2
1. a.
1
2
−
4
π
2
cos(πx) +
1
9
cos(3πx) +
1
25
cos(5πx) +···
;
Chapter 1 447
b.
4
π
sin
πx
2
+
1
3
sin
3πx
2
+
1
5
sin
5πx
2
+···
;
c.
1
12
−
1
π
2
cos(2πx) −
1
4
cos(4πx) +
1
9
cos(6πx) −···
.
3.
¯
f (x ) = f (x −2na),2na < x < 2(n +1)a,
f (x ) ∼ a
0
+
∞
1
a
n
cos(nπx/a) +b
n
sin(nπx/a),
a
0
=
1
2a
2a
0
f (x)dx, a
n
=
1
a
2a
0
f (x ) cos(nπx /a)dx,
b
n
=
1
a
2a
0
f (x ) sin(nπx/a)dx.
5. Odd: (a), (d), (e); even: (b), (c); neither: (f).
7. a.
2
π
sin(πx) −
1
2
sin(2πx) +···
;
b. This function is its own Fourier series;
c.
4
π
2
sin(πx) −
1
9
sin(3πx) +
1
25
sin(5πx) −···
.
9. If f (−x) =−f (x) and f (x) = f (a − x) for 0 < x < a, sine coefficients
with even indices are zero. Example: square wave.
11. a. f (x) =1 =
2
π
∞
1
1 −cos(nπ)
n
sin
nπx
a
;
b. f (x) =
a
2
−
2a
π
2
∞
1
1 −cos(nπ)
n
2
cos
nπx
a
=
2a
π
∞
1
−cos(nπ)
n
sin
nπx
a
;
c. f (x) =
∞
1
(−1)
n+1
sin(1)
2nπ
(nπ)
2
−1
sin(nπx), 0 < x < 1
=
∞
1
(−1)
n
cos(1) −1
2
(nπ)
2
−1
cos(nπx), 0 < x < 1;
d. f (x) =
2
π
1 −
∞
1
1 +cos(nπ)
n
2
−1
cos(nx)
=sin(x).
13. Even, yes. Odd, yes only if f (0) = f (a) = 0.
