Powers D.L. Boundary Value Problems and Partial Differential Equations

Подождите немного. Документ загружается.

408 Chapter 7 Numerical Methods

∂

∂x

∂u

∂t

, u(0, t) = 0,

∂u

∂x

(1, t) +u(1, t) = 1, u(x, 0) = 0.

∂

∂x

∂u

∂t

∂u

∂x

(0, t) = 0, u(1, t) = 1, u(x, 0) = x.

7.3 Wave Equation

The simple vibrating string problem we studied in Chapter 3,

∂

∂x

∂

∂t

, 0 < x < 1, 0 < t, (1)

u(0, t) = 0, u(1, t) = 0, 0 < t, (2)

u(x, 0) = f (x),

∂u

∂t

(x, 0) = g(x), 0 < x < 1, (3)

rarely needs treatment by numerical methods, because the d’Alembert solu-

tion provides a simple and direct means of calculating the solution u(x, t) for

arbitrary x and t. However, if the partial differential equation contains u or an

inhomogeneity or if the boundary conditions are more complex, a series solu-

tion or a solution of the d’Alembert type may not be practical. In many such

cases, simple numerical techniques are quite rewarding.

In order to convert the wave equation (1) into a suitable difference equa-

tion, we ﬁrst designate points x

= i x(x = 1/n) and times t

= m t for

which the approximation to u will be found: u(x

, t

)

∼

(m). Then the par-

tial derivatives with respect to both x and t are replaced by central differences:

∂

∂x

→

i+1

(m) −2u

(m) +u

i−1

(m)

(x)

∂

∂t

→

(m +1) −2u

(m) +u

(m −1)

(t)

The wave equation (1) becomes this partial difference equation

i+1

(m) −2u

(m) +u

i−1

(m)

(x)

(m +1) −2u

(m) +u

(m −1)

(t)

or, with ρ =t/x,

(m +1) −2u

(m) +u

(m −1) = ρ



i+1

(m) −2u

(m) +u

i−1

(m)



The replacement equations may be solved for the unknowns u

(m + 1),

yielding the equation

(m +1) = ρ

i−1

(m) +2(1 −ρ

(m) +ρ

i+1

(m) −u

(m −1), (4)

7.3 Wave Equation 409

valid for i = 1, 2,...,n −1. Naturally, the boundary conditions, Eq. (2), carry

over as u

(m) =0, u

(m) =0. It is obvious that Eq. (4) requires us to know the

approximate solution at time levels m and m −1inordertoﬁnditattimelevel

m +1. In other words, to get u

(1) we need u

i−1

(0), u

i+1

(0) —whichare

available from the initial condition — and also u

(−1)!Ofcourse,wehavenot

yet applied the second initial condition,

∂u

∂t

(x, 0) = g(x), 0 < x < 1.

If we replace the time derivative by a central difference approximation, this

equation translates into

(1) −u

(−1)

2 t

=g(x

) (5)

for i = 1, 2,...,n − 1. Equation (5), together with a slightly modiﬁed version

of Eq. (4) (with m = 0andu

(0) = f (x

)), yields the system

(1) +u

(−1) =ρ

f (x

i−1

) +2



1 −ρ



f (x

) +ρ

f (x

i+1

(1) −u

(−1) =2 tg(x

(6)

which we can easily solve for the u ’s at the ﬁrst time level:

(1) =

f (x

i−1

) +



1 −ρ



f (x

) +

f (x

i+1

) +tg(x

). (7)

Thus,inordertosolvetheprobleminEqs.(1)–(3)numerically,weusethe

initial condition, u

(0) =f (x

), to ﬁll the ﬁrst line of our table, use the starting

equation (7) to ﬁll the next line, and continue with the running equation (4) to

ﬁll subsequent lines.

Example.

Let us now attempt to solve a simple problem. Suppose that g(x) ≡ 0 for 0 <

x < 1andthatf (x) is given by

f (x ) =



2x, 0 < x <

2(1 −x),

< x < 1.

(8)

Also, we shall choose n = 4andρ = 1 for convenience. (That is, t = x =

1/4.) Our rule for calculation, Eq. (4), is then

(m +1) = u

i−1

(m) +u

i+1

(m) −u

(m −1). (9)

In Table 6 are the calculated values of u

(m). Entries in italics are given data.

It is easy to check that this numerical solution is identical with the d’Alembert

solution of this particular problem. (See Exercise 6.) However, if the initial

410 Chapter 7 Numerical Methods

m 01234

0 00.51 0.50

1 0 0.50.50.5 0

2 0 0000

3 0 −0.5 −0.5 −0.5 0

4 0 −0.5 −1 −0.5 0

5 0 −0.5 −0.50.5 0

6 0 0000

Tab le 6 Numerical solution of Eqs. (1)–(3)

velocity were not identically zero, the numerical solution would in general be

only an approximation to the true solution.



Stability

In our study of the heat equation, Section 7.2, we saw that the choice of x and

t was not free. The same is true for the wave equation. Suppose we attempt

to solve the same problem as earlier, but with ρ

= (t/x)

chosen to be 2.

Then Eq. (4) becomes

(m +1) = 2



i−1

(m) −u

(m) +u

i+1

(m)



−u

(m −1),

and the “solution” corresponding to this rule of calculation is shown in Table 7

(again, entries in italics are given data). Of course, the results bear no resem-

blance to the solution of the wave equation. They suffer from the same sort of

instability as that observed in Section 7.2. There is a rule of thumb, similar to

theonetobefoundthere,applicabletothewaveequation.

First, write out the equations for each u

(m + 1) in terms of the u’s at time

levels m and m −1:

(m +1) = a

i−1

(m) +b

(m) +c

i+1

(m) −u

(m −1).

The coefﬁcients must satisfy two conditions:

1. None of the coefﬁcients a

, b

, c

may be negative.

2. The sum of the coefﬁcients is not greater than 2:

≤2.

Of course, u

(m − 1) appears with a coefﬁcient of −1; nothing can be done

about that, nor does it enter into the aforementioned rules.

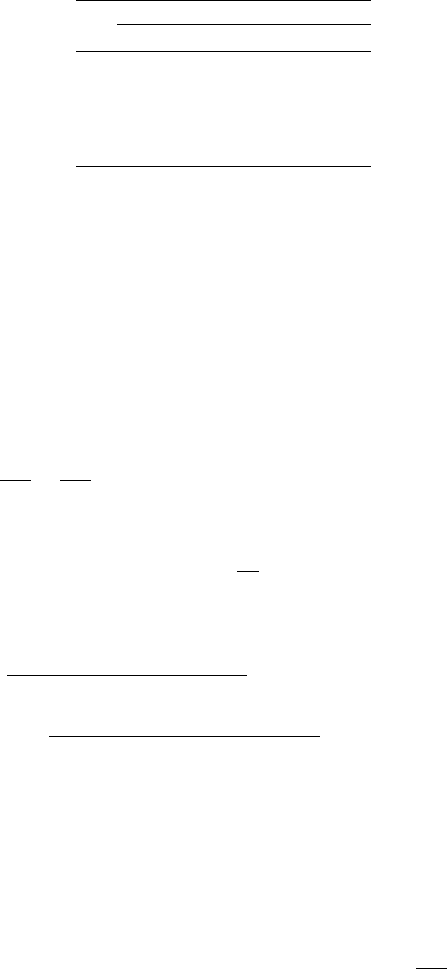
7.3 Wave Equation 411

m 01234

0 00.51 0.50

1 0 0.50 0.5 0

2 0 −1.51−1.5 0

3 0 4.5 −84.5 0

4 0 −23.533−23.5 0

Tab le 7 Unstable numerical solution

In Eq. (4) we see that both conditions are met when ρ =t/x is less than

or equal to 1; in other words, the time step must not exceed the space step.

However, using ρ

=1 when acceptable often provides the best accuracy.

We conclude with one more example, illustrating how numerical results can

be obtained easily in some cases that might be puzzling analytically.

Example.

Supposewearetosolvetheproblem

∂

∂x

∂

∂t

−16 cos(π t), 0 < x < 1, 0 < t, (10)

u(0, t) = 0, u(1, t) = 0, 0 < t, (11)

u(x, 0) = 0,

∂u

∂t

(x, 0) = 0, 0 < x < 1. (12)

We replace the partial derivatives as before, obtaining

i+1

(m) −2u

(m) +u

i−1

(m)

(x)

(m +1) −2u

(m) +u

(m −1)

(t)

−16 cos(π t

When this is solved for u

(m +1),weﬁnd

(m +1) = (2 −2ρ

(m) +ρ

i+1

(m) +ρ

i−1

(m)

−u

(m −1) +16(t)

cos(πm t). (13)

Let us take x = t = 1/4again,soρ = 1 and Eq. (13) simpliﬁes to

(m +1) = u

i+1

(m) +u

i−1

(m) −u

(m −1) +cos



mπ



. (14)

This is our running equation. The starting equation comes from combining

Eqs. (14) for m = 0,

(1) =−u

(−1) +1

412 Chapter 7 Numerical Methods

m 01234

0 00000

1 0 0.50.50.5 0

2 0 1.21 1.71 1.21 0

3 0 1.21 1.91 1.21 0

4 0 0.00 0.00 0.00 0

5 0 −2.21 −2.91 −2.21 0

6 0 −3.62 −5.12 −3.62 0

7 0 −2.91 −4.33 −2.91 0

Tab le 8 Numerical solution of Eqs. (10)–(12)

(note u

(0) =0), with the replacement initial condition

(1) −u

(−1)

2 t

=0,

(1) = u

(−1) =

for i =1, 2, 3. Now we have the top two lines of Table 8, and the rest are ﬁlled

using Eqs. (14) (with cos(π/4)  0.71, and so forth). Entries in italics are given

data.

Thecompleteanalyticalsolutionofthisproblemis

u(x, t) =

t sin(πt) sin(π x)

∞



n=3

1 −cos(nπ)

n(n

−1)



cos(πt) −cos(nπ t)



sin(nπx).

At x = 1/2, the sum of the inﬁnite series is 0, so



, t



t sin(πt).

Comparison of the values of this function at times t

with the middle column

of Table 8 shows the numerical solution off by a few percent. Note that the

growth in u(x, t) is due to resonance in the physical system, not to numerical

instability.



EXERCISES

1. Obtain an approximate solution of Eqs. (1), (2), and (3) with f (x) ≡ 0and

g(x) ≡ 1. Take x = 1/4, ρ = 1.

7.3 Wave Equation 413

2. Compare the results of Exercise 1 with the d’Alembert solution.

3. Obtain an approximate solution of Eqs. (1), (2), and (3) with f (x) ≡ 0and

g(x) = sin(π x).Takex = 1/4, ρ = 1.

4. Compare the results of Exercise 3 with the exact solution u(x, t) =

(1/π) sin(πx) sin(π t).

5. Obtain an approximate solution of Eqs. (1), (2), and (3) with g(x) ≡ 0and

f (x) asinEq.(8).Usex = 1/4andρ

=1/2.

6. Compare the entries of Table 6 with the d’Alembert solution.

7. Obtain an approximate solution of this problem with a time-varying

boundary condition, using x =t = 1/4.

∂

∂x

∂

∂t

, 0 < x < 1, 0 < t,

u(0, t) = 0, u(1, t) = h(t), 0 < t,

u(x, 0) = 0,

∂u

∂t

(x, 0) = 0, 0 < x < 1,

h(t) =



1, 0 < t < 1,

−1, 1 < t < 2

and h(t + 2) = h(t), h(0) = h(1) = 0.

8. Same task as Exercise 7 but h(t) = sin(πt). Use sin(π/4)

∼

0.7 instead of

√

2/2.

9. Find starting and running equations for the following problem. Using

x = 1/4, ﬁnd the longest stable time step and compute values of the

approximate solution for m up to 8.

∂

∂x

∂

∂t

+16u, 0 < x < 1, 0 < t,

u(0, t) = 0, u(1, t) = 0, 0 < t,

u(x, 0) = f (x),

∂u

∂t

(x, 0) = 0, 0 < x < 1,

where f (x) is given in Eq. (8).

10. Using x = 1/4andρ

= 1/2, compare the numerical solution of the

problem in Exercise 9 with and without the 16u term in the partial differ-

ential equation.

414 Chapter 7 Numerical Methods

7.4 Potential Equation

In this section, we will be concerned with approximate solutions of the po-

tential equation and related equations in a region

R of the xy-plane. For the

sake of simplicity, we will limit ourselves to regions whose boundaries can be

made to coincide with the lines on a sheet of graph paper with square divi-

sions. Thus, we admit such shapes as rectangles, L’s and T’s, but not circles or

triangles. The graph paper provides us with a ready-made mesh of points in

the region

R and on its boundary, at which we wish to know the solution of

ourproblem.Thesepointsaretobenumberedinsomefashion—usuallyleft

to right and bottom to top.

On such a mesh, the replacement for the Laplacian operator is the following:

∂

∂x

∂

∂y

→

−2u

(x)

−2u

(y)

, (1)

where the subscripts E, W stand for the indices of the mesh points to the left

and right of point i and the subscripts N, S stand for those above and below

(see Fig. 1). The result is sometimes called the ﬁve-point approximation to the

Laplacian. Because we are assuming that x = y,weobtainafurthersim-

pliﬁcation in the replacement:

∂

∂x

∂

∂y

→

−4u

(x)

. (2)

Example.

Solve this problem numerically (see Chapter 4 for the analytical solution):

∂

∂x

∂

∂y

=0, 0 < x < 1, 0 < y < 1, (3)

u(0, y) = 0, u(1, y) = 0, 0 < y < 1, (4)

u(x, 0) = f (x), u(x, 1) = f (x), 0 < x < 1, (5)

f (x) =



2x, 0 < x <

2(1 −x),

≤x < 1.

(6)

Let us take x = y = 1/4 and number the mesh points inside the 1 × 1

square as shown in Fig. 2.

At each of the nine mesh points, we will have the replacement equation

−4u

=0. (7)

Together, these make up a system of nine equations in the nine unknowns

, u

,...,u

. Referring to Fig. 2, where the values of u at boundary points are

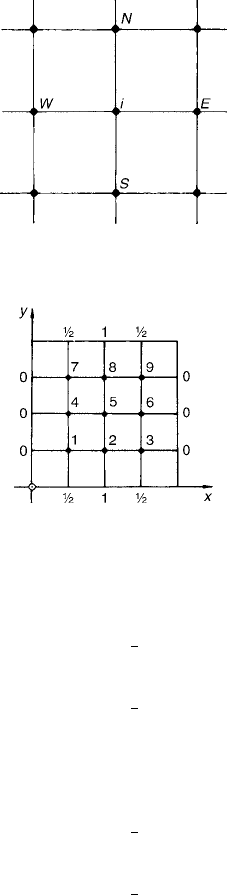
7.4 Potential Equation 415

Figure 1 Point i on a square mesh and its four neighbors.

Figure 2 Numbering for mesh points, and values on boundary.

shown, we can write down the equations to be solved:

−4u

= 0

+1 − 4u

= 0

−4u

= 0

−4u

= 0

−4u

= 0

−4u

= 0

−4u

= 0

+1 − 4u

= 0

−4u

= 0.

(8)

This is simply a system of simultaneous equations. It can be solved by elim-

ination to obtain the results shown in Fig. 3. In this particular case, there are

numerous symmetries in the problem, so u

= u

, u

= u

,and

= u

. Thus, only u

, u

,andu

need to be found. The system can be

reduced to four equations in these four unknowns, which can even be solved

manually.



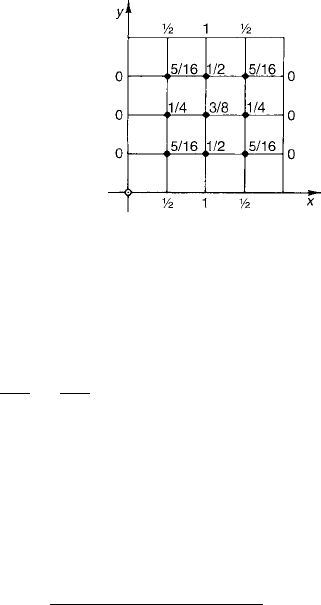
416 Chapter 7 Numerical Methods

Figure 3 Numerical solution of Eqs. (3)–(6).

Example.

Set up the replacement equations for the problem

∂

∂x

∂

∂y

=16(u −1), 0 < x < 1, 0 < y < 1, (9)

u(x, 0) = 0, u(x, 1) = 0, 0 < x < 1, (10)

u(0, y) = 0, u(1, y) = 0, 0 < y < 1. (11)

We may use the same numbering as in the ﬁrst example (Fig. 2). At each mesh

point, the replacement is

−4u

(x)

=16(u

−1). (12)

Because x = 1/4, (1/x)

= 16, and the typical replacement equation be-

comes

−4u

−1,

−5u

=−1. (13)

Finally, we may write out the equations to be solved. The ﬁrst four of the nine

equations, corresponding to Eq. (13) with i = 1, 2, 3, 4, are

−5u

=−1

−5u

=−1

−5u

=−1

−5u

=−1.

(14)

The solution of this problem is left as an exercise.



On more complicated regions, the replacement for the Laplacian operator

hasexactlythesameform,sincewestillusethe“graph-papermesh.”Thesys-

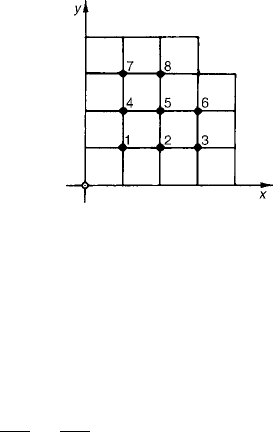
7.4 Potential Equation 417

Figure 4 Mesh numbering for L-shaped region.

tem of equations to be solved will be rather less regular than that for a rectan-

gle.

Example.

Consider the problem

∂

∂x

∂

∂y

=−16 in R, (15)

u = 0 on the boundary of

R, (16)

where

R is an L-shaped region formed from a 1×1squarebyremovinga1/4×

1/4 square from the upper right corner. The general replacement equation is

−4u

=−1. (17)

With the numbering shown in Fig. 4, the eight equations to be solved are

−4u

=−1

−4u

=−1

−4u

=−1

−4u

=−1

−4u

=−1

−4u

=−1

−4u

=−1

−4u

=−1.

(18)

The results, rounded to three digits, are shown in Eq. (19). Note the equalities,

which arise from symmetries in the problem:

= 0.656

= 0.813

= 0.616

= 0.981

= 0.649.

(19)

