Powers D.L. Boundary Value Problems and Partial Differential Equations

Подождите немного. Документ загружается.

418 Chapter 7 Numerical Methods

Iterative Methods

Systems of up to 10 equations, such as those in the foregoing examples, can

readily be solved by elimination. It is easy to see, however, that we might well

want a ﬁner mesh to get better accuracy and that a ﬁner mesh will increase the

number of equations dramatically. For example, if we use x = y = 1/10

in a numerical solution of Eqs. (3)–(5), the system to be solved contains 81

unknowns (or 25 if we use symmetry). Problems involving many thousands of

unknowns are quite common. These large systems of simultaneous equations

are almost always solved by iterative methods, which generate a sequence of

approximate solutions.

Consider again the potential problem in Eqs. (3)–(6). Let us take a mesh

with x = y = 1/N and number the points of the mesh with a double index

so that

u(x

, y

)

∼

i,j

. (20)

Then the replacement equations for the potential equation are

i+1,j

−2u

i,j

i−1,j

(x)

i,j+1

−2u

i,j

i,j−1

(y)

=0,

or, using x = y and some algebra,

i,j

i+1,j

i−1,j

i,j+1

i,j−1

), (21)

valid for i and j ranging from 1 to N − 1. (This is the same as Eq. (7).) The

boundary conditions, Eqs. (4) and (5), determine

0,j

=0, u

N,j

=0, j = 0,...,N, (22)

i,0

=f (x

), u

i,N

=f (x

), i =0,...,N. (23)

The simplest iterative method, called the Gauss–Seidel method, works this

way. We sweep through the array of u’s, replacing each u

i,j

by the combination

of u’s given on the right-hand side of Eq. (21). After several sweeps through

the array, the numbers no longer change much. When the new and old values

of u

i,j

at each point agree closely enough, we stop.

The result is a set of numbers that satisfy Eq. (21) approximately. Since the

exact solution of the replacement equations is still just an approximation to

the solution of the original problem in Eqs. (3)–(6), it is not urgent to get that

exact solution of the replacement equations.

An iterative method such as the Gauss–Seidel method is very easy to imple-

ment on a spreadsheet without programming. (See the CD.)

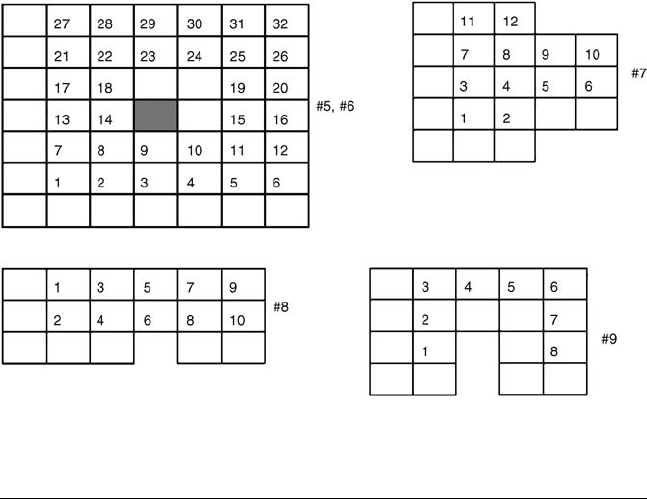
7.4 Potential Equation 419

Figure 5 Regions and mesh numbering for Exercises 5–9.

EXERCISES

Set up and solve replacement equations for each of the following problems.

Use symmetry to reduce the number of unknowns.

1. ∇

u =−1, 0 < x < 1, 0 < y < 1, u = 0 on the boundary. x = y =1/4.

2. Same as Exercise 1 with x = y = 1/8. Compare the solutions.

3. ∇

u = 0, 0 < x < 1, 0 < y < 1, u(0, y) = 0, u(x, 0) = 0, u(1, y) = y,

u(x, 1) = x. x =y = 1/4.

4. Same as Exercise 3 with x = y = 1/8.

5. The region R is a square of side 1 from the center of which a similar square

of side 1/7hasbeenremoved;∇

u = 0inR, u = 0 on the outside bound-

ary, and u = 1 on the inside boundary; x =y = 1/7. See Fig. 5.

6. Same as Exercise 5, but the partial differential equation is ∇

u =−1, and

the boundary condition is u = 0 on all boundaries. See Fig. 5.

7. The region R has the shape of a T, made by removing strips from the cor-

ners of a 1 ×1 square. The partial differential equation is ∇

u =−25 in R,

and u = 0 on the boundary. Take x = y = 1/5. See Fig. 5 for numbering

of mesh points.

8. The region is a rectangle, 2 units wide and 1 unit high. The potential equa-

tionholdsintheinterior;u =1 on the upper half of the boundary (the top

420 Chapter 7 Numerical Methods

and the upper halves of the vertical sides), and u = 0 on the lower half. Take

x = y =1/3. See Fig. 5.

9. The region, as seen in Fig. 5, is shaped like an upside-down U and is formed

by removing a small (1 × 2) rectangle from the bottom of a larger (5 ×4)

one. In the interior of the region, ∇

u = 0. The boundary conditions are:

u = 1 on the left and right sides and the top of the rectangle; u = 0onthe

bottom and on the boundary formed by the removal of the small rectangle.

Use x = y =1.

7.5 Two-Dimensional Problems

Separation of variables and other analytical methods produce satisfactory so-

lutions to two-dimensional problems in only the nicest cases. However, simple

numerical methods work quite well on two-dimensional problems. In this ele-

mentary exposition, we will limit ourselves to the heat and wave equations on

two-dimensional regions that “ﬁt on graph paper,” as in Section 7.4.

We will compute an approximation to the solution of a problem, denot-

ing space position with one or two subscripts and time level with an index in

parentheses. Both heat and wave problems will require the replacement of the

Laplacian operator. We use the same replacement as in Section 7.4,

∂

∂x

∂

∂y

→

(m) −2u

(m) +u

(m)

(x)

(m) −2u

(m) +u

(m)

(y)

Because we are using a square mesh, with x =y, the replacement simpliﬁes

∂

∂x

∂

∂y

→

(m) +u

(m) −4u

(m)

(x)

, (1)

where N, S, E, W stand for the indices of the four grid points adjacent to the

point with the index i.

Heat Problems

Now let us consider this heat problem on a rectangle:

∂

∂x

∂

∂y

∂u

∂t

, 0 < x < 1.25, 0 < y < 1, 0 < t, (2)

u(0, y, t) = 0, u(1.25, y, t) = 0, 0 < y < 1, 0 < t, (3)

u(x, 0, t) = 0, u(x, 1, t) = 0, 0 < x < 1.25, 0 < t, (4)

u(x, y, 0) = 1, 0 < x < 1.25, 0 < y < 1. (5)

7.5 Two-Dimensional Problems 421

Figure 6 Mesh numbering for numerical solution of Eqs. (2)–(5).

We ta ke x = y = 1/4 and number the interior points of the region as

shown in Fig. 6. Then we will be computing the approximations

(m)

∼



, t



, u

(m)

∼



, t



, u

(m)

∼



, t



,...

(6)

and so forth, for m = 1, 2,.... The replacement equations are obtained using

Eq. (1) for the Laplacian and a forward difference to replace the time deriva-

tive. The typical equation is

(m) +u

(m) −4u

(m)

(x)

(m +1) −u

(m)

t

. (7)

Whenwesolvethisequationforu

(m +1),weobtain

(m +1) = r[u

(m) +u

(m)] +(1 −4r)u

(m), (8)

in which

r =

t

x

t

y

=16 t.

The stability considerations of Section 7.2 are still important, and the rules of

thumb are still valid. We must limit r by the requirement that 1 −4r ≥ 0, or, in

this case, t ≤1/64. We shall take the longest acceptable time step, t =1/64,

r =1/4, which makes the equations a little simpler.

At m = 0,alltemperaturesaregivenas1.Form ≥ 1, all the boundary tem-

peratures are zero and the u

(m) are all found to equal 1. For m = 2, we calcu-

late

(2) =



(1) +u

(1) +0 +0



(2) =



(1) +u

(1) +0



422 Chapter 7 Numerical Methods

m 1256

01111

Tab le 9 Numerical solution of Eqs. (2)–(5)

(2) =



(1) +u

(1) +0



(2) =



(1) +u

(1)



=1.

The 0’s in these equations stand for boundary temperatures.

An alert calculator will notice that only the unknowns u

, u

need be

calculated, since, in this example, the others will be given at each time step by

symmetry

(m) =u

(m), u

(m) =u

(m),

(m) =u

(m), u

(m) =u

(m).

InTable9arecomputedvaluesofthesigniﬁcantu’s at a few times.

Now consider this heat problem, which is not solvable by separation of vari-

ables:

∂

∂x

∂

∂y

∂u

∂t

R, (9)

u =f (t) on

C, (10)

u =0in

R at t =0. (11)

Here,

R is an L-shaped region and C is its boundary. The function f we take

to be f (t) = t, but more complicated functions can be used.

To start the numerical solution, we set up a square grid, as shown in Fig. 7.

The spacing is x =y = 1/5 and the numbering of the points is shown. The

typical replacement equation is just as given in Eqs. (7) and (8). We must bear

in mind, however, that some points are adjacent to boundary points where the

temperature is given by f (t).

7.5 Two-Dimensional Problems 423

Figure 7 Mesh numbering for numerical solution of Eqs. (9)–(11).

Because x = y = 1/5, the parameter r in Eq. (8) is

r =

t

x

=25 t.

Clearly, the longest stable time step is t =1/100, corresponding to r = 1/4.

Using this value of r simpliﬁes the typical replacement equation to

(m +1) =



(m) +u

(m)



. (12)

Speciﬁcally, we have

(m +1) =



(m) +u

(m) +2f (t

)



(m +1) =



(m) +u

(m) +f (t

)



and so on. The f (t

) terms enter because point 1 is adjacent to two boundary

points and point 2 to one boundary point. Note that symmetry about the line

through points 4 and 7 makes it unnecessary to compute u

(m),...,u

(m).

Table 10 contains calculated values of u for the ﬁrst four time levels.

Wave Problems

In solving two-dimensional wave problems, we replace the Laplacian, as in the

foregoing, and use a central difference for the time derivative, as we did in

Section 7.3:

∂

∂t

→

(m +1) −2u

(m) +u

(m −1)

t

. (13)

424 Chapter 7 Numerical Methods

m 1234567f (t

)

00000000 0

10000000 1.0

20.50.25 0.25 0.50.50.25 0 2.0

31.22 0.75 0.69 0.75 1.22 0.69 0.25 3.0

41.99 1.40 1.19 1.84 1.98 1.30 0.69 4.0

Tab le 1 0 Numerical solution of Eqs. (9)–(11). Entries are 100 ×u

(m)

As an example, let us consider the vibrations of a square membrane, as de-

scribed by the problem

∂

∂x

∂

∂y

∂

∂t

, 0 < x < 1, 0 < y < 1, 0 < t, (14)

u(x, 0, t) = 0, u(x, 1, t) = 0, 0 < x < 1, 0 < t, (15)

u(0, y, t) = 0, u(1, y, t) = 0, 0 < y < 1, 0 < t, (16)

u(x, y, 0) = f (x, y), 0 < x < 1, 0 < y < 1, (17)

∂u

∂t

(x, y, 0) = g(x, y), 0 < x < 1, 0 < y < 1. (18)

A typical replacement for the wave equation (14) is constructed using Eq. (1)

for the Laplacian and Eq. (13) for the time derivative:

(m +1) −2u

(m) +u

(m −1)

(t)

(m) +u

(m) −4u

(m)

(x)

. (19)

As usual we solve for u

(m +1), using the abbreviation ρ = t/x.Theresult

(m +1) = ρ



(m) +u

(m)



+(2 − 4ρ

(m) −u

(m −1). (20)

The stability rules given earlier still apply. Thus we must choose ρ

≤ 1/2in

order to get a sensible solution.

Let us now be speciﬁc. We shall take x = y = 1/4, ρ

= 1/2 (that is,

t = 1/4

√

2), and suppose that the initial data from Eqs. (11) and (12) are

f (x, y) =



1nearx =

, y =

0elsewhere,

g(x, y) ≡ 0.

7.5 Two-Dimensional Problems 425

The running equation is Eq. (20), which, with ρ

=1/2, simpliﬁes to

(m +1) =



(m) +u

(m)



−u

(m −1). (21)

To ﬁnd the starting equation we solve Eq. (21) with m = 0 together with the re-

placement equation for the initial-velocity condition, Eq. (18). The equations

are

(1) +u

(−1) =



(0) +u

(0)



, (22)

(1) −u

(−1) = 2 tg

. (23)

Because g(x, y) = 0 in this instance, we ﬁnd

(1) =



(0) +u

(0)



as the starting equation; the right-hand side contains known values of u only.

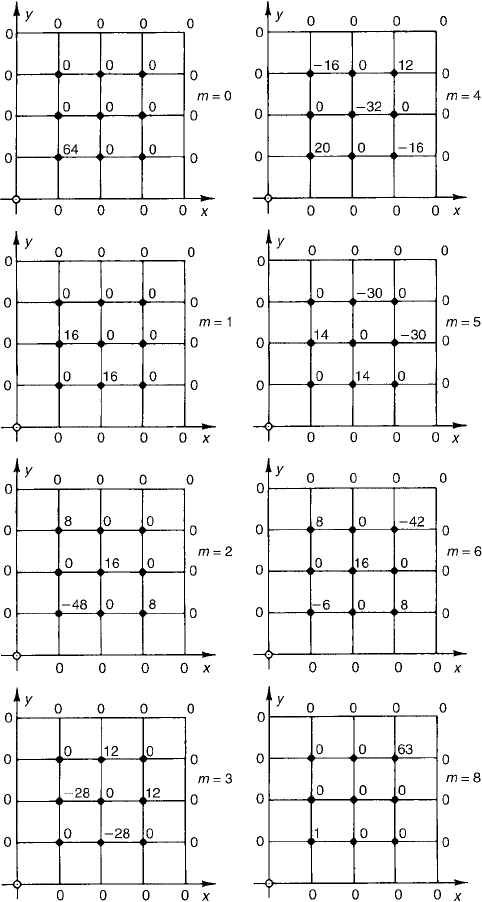
In Fig. 8 are representations of the numerical solution at various time levels.

Thesimplenumericaltechniquewehavedevelopedcanbeadaptedeasily

to treat inhomogeneities, boundary conditions involving derivatives of u,or

time-varying boundary conditions. Even nonrectangular regions can be han-

dled, provided they ﬁt neatly on a rectangular grid. Several exercises illustrate

these points.

EXERCISES

In Exercises 1–5, set up replacement equations using the given space mesh and

the numbering shown in the ﬁgure cited. Then ﬁnd the u

(m) for a few values

of m using the largest stable value of r. Let boundary conditions override the

initial condition if there is a disagreement.

1. ∇

u =

∂u

∂t

,0< x < 1, 0 < y < 0.75, 0 < t,

u(0, y, t) = 0, u(1, y, t) = 0, 0 < y < 0.75, 0 < t,

u(x, 0, t) = 0, u(x, 0.75, t) = 1, 0 < x < 1, 0 < t,

u(x, y, 0) = 0, 0 < x < 1, 0 < y < 0.75,

x = y =1/4. (See Fig. 9a.)

2. ∇

u =

∂u

∂t

R,0< t

u =0onboundary,0< t

u =1in

R, t =0.

426 Chapter 7 Numerical Methods

Figure 8 Displacements of the square membrane. Numbers shown are

(m) ×64.

The region R is an inverted T: Starting with a rectangle of width 1 and

height 3/4, remove a 1/4 × 1/4squarefromtheupperleftandrightcor-

ners. Take x = y = 1/4. (See Fig. 9b.)

7.5 Two-Dimensional Problems 427

Figure 9 Regions for Exercises 1–3.

Same as Exercise 2, except that the region is a cross. (See Fig. 9c.)

4. Same as Eqs. (9)–(11), except that the boundary condition is u = 1onthe

bottom (y = 0) and u = 0 elsewhere. (See Fig. 7.)

5. ∇

u =

∂u

∂t

,0< x < 1, 0 < y < 1, 0 < t,

u(0, y, t) = 0, u(1, y, t) = 1, 0 < y < 1, 0 < t,

u(x, 0, t) = 0, u(x, 1, t) = 1, 0 < x < 1, 0 < t,

u(x, y, 0) = 0, 0 < x < 1, 0 < y < 1,

x = y =1/4. (See Fig. 2.)

6. Find a numerical solution of the heat problem on a 1×1 square with x =

y = 1/4. Initially u = 0 and on the outside boundary u = 0. There is a

tiny hole in the center of the square, so u(1/2, 1/2, t) = 1, t > 0. (Actually,

the region is a punctured square.)

7. Solve numerically Eqs. (14)–(18) with x = y = 1/4, ρ

= 1/2. Take

f (x, y) ≡ 0and

g(x, y) =



√

2at





0elsewhere.

Physically, u describes the vibrations of a square membrane struck in the

middle.

8. Obtain an approximate solution of Eqs. (14)–(18) with f (x, y) ≡ 0and

g(x, y) =4

√

2. Take x = y =1/4andρ

=1/2.

9. Same as Exercise 8, but f (x, y) ≡ 1andg(x, y) ≡0inthesquare.

10. Obtain an approximate numerical solution to the wave equation on an L-

shaped region (a 1 ×1 square with a 1/4 ×1/4squareremovedfromthe

upper right corner). Assume initial displacement = 1 in the lower right

corner, initial velocity equal to 0, and zero displacement on the boundary.

Ta ke x =y = 1/4andρ

=1/2.