Powers D.L. Boundary Value Problems and Partial Differential Equations
Подождите немного. Документ загружается.


458 Answers to Odd-Numbered Exercises
In the integral for b
n
, break the interval of integration at a; in the second
integral, make the change of variable y = 2a −x. The two integrals cancel
if n is even, and the coefficient is the same as Eq. (18) if n is odd.
b. In the solution of Eqs. (1)–(4), the eigenfunction φ(x) = sin((2n −
1)πx/2a) has the property φ(2a − x) = φ(x),sothesumoftheseries
has the same property. This implies 0 derivative at x = a.
15. W(t) = C
0
LA
1 −
∞
n=1
2e
−(λ
2
n
Dt)
(n −1/2)
2
π
2
.
Section 2.6
1. The graph of v(x) is a straight line from T
0
at x =0toT
∗
at x =a,where
T
∗
=T
0
+
ha
k +ha
(T
1
−T
0
).
In all cases, T
∗
is between T
0
and T
1
.
3. Negative solutions provide no new eigenfunctions.
7. b
m
=
2(1 −cos(λ
m
a))
λ
m
[a +(κ/h) cos
2
(λ
m
a)]
.
9. b
m
=
−2(κ +ah) cos(λ
m
a)
λ
m
(ah +κ cos
2
(λ
m
a))
.
Section 2.7
1. λ
n
=nπ/ln 2, φ
n
=sin(λ
n
ln(x)).
3. a. sin(λ
n
x), λ
n
=(2n −1)π/2a;
b. cos(λ
n
x), λ
n
=(2n −1)π/2a;
c. sin(λ
n
x), λ
n
asolutionoftan(λa) =−λ;
d. λ
n
cos(λ
n
x) + sin(λ
n
x), λ
n
a solution of cot(λa) = λ;
e. λ
n
cos(λ
n
x) +sin(λ
n
x), λ
n
asolutionoftan(λa) = 2λ/(λ
2
−1).
5. The weight functions in the orthogonality relations and limits of integra-
tion are:
a. 1 +x,0toa;b.e
x
,0toa;c.
1
x
2
,1to2; d.e
x
,0toa.
7. Because λ appears in a boundary condition.
9. The negative value of µ does not contradict Theorem 2 because the coef-
ficient α
2
is not positive.

Chapter 2 459
Section 2.8
1. x =
∞
n=1
c
n
φ
n
,1< x < b; c
n
=2nπ
1 −b cos(nπ)
n
2
φ
2
+ln
2
(b)
.
3. 1 =
∞
n=1
c
n
φ
n
,0< x < a; c
n
=2nπ
1 −e
a/2
cos(nπ)
n
2
π
2
+a
2
/4
.
(Hint: Find the sine series of e
x/2
.)
5. b
n
=
r
l
f (x)ψ
n
(x)p(x)dx.
7. 1 and
√
2cos(nπx), n = 1, 2,....
Section 2.9
1. a. v(x) = constant; b. v(x) = AI(x) +B.
3. If ∂u/∂x =0 at both ends, then the steady-state problem is indeterminate.
But Eqs. (1)–(3) are homogeneous, so separation of variables applies di-
rectly. Note that λ
0
= 0andφ
0
= 1. The constant term in the series for
u(x, t) is
a
0
=
r
l
p(x)f (x)dx
r
l
p(x)dx
.
Section 2.10
1. The solution is as in Eq. (9), with B(λ) = 2T(cos(λa) − cos(λb))/λπ .
3. u(x, t) is given by Eq. (6) with B(λ) =
2T
0
λ
π(α
2
+λ
2
)
.
5. u(x, t) =
∞
0
A(λ) cos(λx) exp
−λ
2
kt
dλ;
A(λ) =
2T
πλ
sin(λb) −sin(λa)
.
7. u(x, t) = T
0
+
∞
0
B(λ) sin(λx) exp
−λ
2
kt
dλ;
B(λ) =
2
π
∞
0
f (x ) −T
0
sin(λx)dx.
9. a. v(x) = C
0
e
−ax
;
b.
∂w
∂t
=D
∂
2
w
∂x
2
−a
2
w
,0< x,0< t,
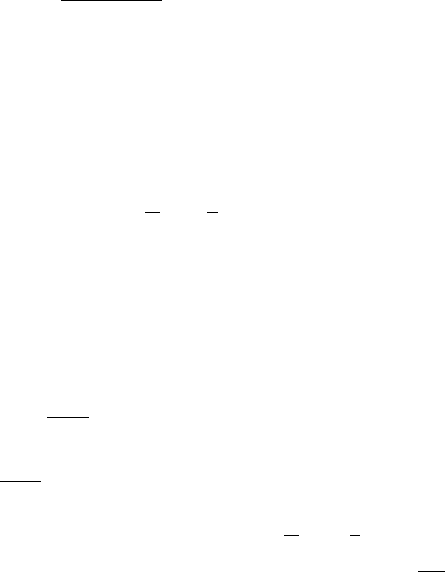
460 Answers to Odd-Numbered Exercises
w(0, t) = 0, 0 < t,
w(x, 0) =−C
0
e
−ax
,0< x;
c. w(x, t) = e
−a
2
Dt
∞
0
B(λ) sin(λx)e
−λ
2
Dt
dλ,
B(λ) =−2C
0
λ/
π
λ
2
+a
2
.
Section 2.11
1. Break the interval of integration at x
=0.
3. B(λ) = 0, A(λ) =
2T
0
a
π(1 +λ
2
a
2
)
.
5. The function u(x, t), as a function of x, is the famous “bell-shaped” curve.
The smaller t is, the more sharply peaked the curve.
7. In Eq. (3) replace both f (x
) and u(x, t) by 1.
9. Using the integral given, obtain
u(x, t) =
2
π
∞
0
1
λ
sin(λx)e
−λ
2
kt
dλ.
Note, however, that B(λ) = 2/λπ is not found using the usual formulas
for Fourier coefficient functions.
Section 2.12
5. As t →0+, x/
√
4πkt →
+∞ if x > 0,
−∞ if x < 0,
so erf(x/
√
4πkt ) →
+1ifx > 0,
−1ifx < 0.
7. Make the substitution x =y
2
.ThenI(x) =
√
π erf(
√
x) +c.
9. Let z be defined by erf(z) =−U
b
/(U
i
−U
b
).Thenx(t) = z
√
4kt.
Chapter 2 Miscellaneous Exercises
1. SS: v(x) = T
0
,0< x < a.
EVP: φ
+ λ
2
φ = 0, φ(0) = 0, φ(a) = 0, λ
n
= nπ/a, φ
n
= sin(λ
n
x),
n =1, 2,....

Chapter 2 461
u(x, t) = T
0
+
∞
1
b
n
sin(λ
n
x)e
−λ
2
n
kt
,
b
n
=
2
a
a
0
(T
1
−T
0
) sin
nπx
a
dx .
3. SS: v(x) = T
0
+
r
2
x(x −a),0< x < a.
EVP: φ
+ λ
2
φ = 0, φ(0) = 0, φ(a) = 0, λ
n
= nπ/a, φ
n
= sin(λ
n
x),
n =1, 2,....
u(x, t) = T
0
−
r
2
x(x −a) +
∞
1
b
n
sin(λ
n
x) exp
−λ
2
n
kt
,
b
n
=
2
a
a
0
T
1
−T
0
+
r
2
x(x −a)
sin
nπx
a
dx .
5. SS: not needed.
(Hint: Put −γ
2
u on the other side of the equation. Separation of vari-
ables gives φ
/φ = γ
2
+T
/kT =−λ
2
.)
EVP: φ
+ λ
2
φ = 0, φ
(0) = 0, φ
(a) = 0, λ
0
= 0, φ
0
= 1; λ
n
= nπ/a,
φ
n
=cos(λ
n
x), n = 1, 2,....
u(x, t) = e
−γ
2
kt
a
0
+
a
n
cos(λ
n
x) exp
−λ
2
n
kt
.
a
0
=T
1
/2, a
n
=−2T
1
1 −cos(nπ)
/n
2
π
2
.
7. u(x, t) = T
0
.
9. u(x, t) = T
0
+
∞
n=1
c
n
sin(λ
n
x) exp
−λ
2
n
kt
,
λ
n
=
(2n −1)π
2a
, c
n
=
(T
1
−T
0
) ·4
(2n −1)π
.
11. u(x, t) = T
0
+
∞
0
B(λ) sin(λx) exp
−λ
2
kt
dλ, B(λ) =
−2λT
0
π(α
2
+λ
2
)
.
13. u(x, t) =
∞
0
A(λ) cos(λx) exp
−λ
2
kt
dλ, A(λ) =
2T
0
sin(λa)
πλ
.
15. u(x, t) =
∞
0
A(λ) cos(λx) +B(λ) sin(λx)
exp
−λ
2
kt
dλ,
A(λ) =
T
0
sin(λa)
πλ
, B(λ) =
T
0
(1 −cos(λa))
πλ
or

462 Answers to Odd-Numbered Exercises
u(x, t) =
T
0
√
4πkt
a
0
exp
−
(x
−x )
2
4kt
dx
=
T
0
2
erf
a −x
√
4kt
+erf
x
√
4kt
.
17. Interpretation: u is the temperature in a rod with insulation on the cylin-
drical surface and on the left end. At the right end, heat is being forced
into the rod at a constant rate (because q(a, t) =−κ
∂u
∂x
(a, t) =−κS,so
heat is flowing to the left, into the rod). The accumulation of heat energy
accounts for the steady increase of temperature.
19. (1/6ka)u
3
−(a/6k)u
1
satisfies the boundary conditions.
21. w(x, t) =−
2
u
∂u
∂x
,whereu(x, t) = a
0
+
a
n
cos(nπx) exp
−n
2
π
2
t
,
where a
0
=2
1 −e
−1/2
and a
n
=
1 −e
−1/2
cos(nπ)
1
4
+(nπ)
2
.
23. u
2
=T
0
β
2
V
β
1
+β
2
, u
1
=T
0
1 −
β
1
V
β
1
+β
2
,
where V =1 −exp(−(β
1
+β
2
)t) and β
i
=h/c
i
.
25. u(ρ, t) =
1
ρ
∞
n=1
b
n
sin(λ
n
ρ)exp
−λ
2
n
kt
,
λ
n
=nπ/a, b
n
=
2
a
a
0
ρT
0
sin(λ
n
ρ)dρ.
27. v(x) = T
0
+Sx −S
sinh(λx)
γ cosh(γ a)
.
29. If λ = 0, the differential equation is φ
=0 with general solution φ(x) =
c
1
+c
2
x . The boundary conditions require c
2
=0butallowc
1
=0. Thus,
this value of λ permits the existence of a nonzero solution, and therefore
λ =0isaneigenvalue.
31. Choose B(ω) =
2
π
∞
0
f (t) sin(ωt)dt.Iff has a Fourier integral represen-
tation, then this choice of B will make u(0, t) = f (t),0< t.
33. a. v(x) =−Ix/aK +c
1
+c
2
(1 −e
−aKx/T
),
c
1
=h
1
, c
2
=(h
2
−h
1
+IL/aK)/(1 −e
−aKL/T
).
b.
∂
2
w
∂x
2
+µ
∂w
∂x
=
1
k
∂w
∂t
,0< x < L,0< t,
w(0, t) = 0, w(L, t) = 0, 0 < t,
w(x, 0) = h
0
(x) −v(x),0< x < L,
where µ = aK/T, k = T/S.

Chapter 3 463
c. w(x, t) =
c
n
φ
n
(x)e
−λ
2
n
kT
, φ
n
(x) = e
−µx/2
sin(nπx/L),
λ
2
n
=
nπ
L
2
+
µ
2
4
;
d. λ
2
n
=(7.30n
2
+0.0133) × 10
−4
m
−1
.
35. a.
∂u
∂t
=D
∂
2
u
∂x
2
,0< x < L,0< t,
∂u
∂x
(0, t) = 0, u(L, t) = S
0
,0< t;
u(0, t) = 0, 0 < x < L;
b. u(x, t) = S
0
+
∞
n=1
c
n
cos(λ
n
x) exp
−λ
2
n
Dt
,
c
n
=4S
0
(−1)
n
/(2n −1).
37. T(y, t) = 300 − 150y/c +
b
n
sin λ
n
(y + c) exp(−λ
2
n
kt), λ
n
= nπ/2c,
b
n
=(400 cos(nπ)+1000)/nπ. c. Just before time t =0, the three terms
addto0.Justaftertimet = 0, the integrated terms do not change sensi-
bly, but in the first term, near y = c, T(y, t) changes suddenly.
Chapter 3
Section 3.1
1. [u] =L,[c] =L/t.
3. v(x) =
(x
2
−ax)g
2c
2
.
Section 3.2
3. u(x, t) =
∞
n=1
b
n
sin
nπx
a
sin
nπct
a
,
b
n
=
2a(1 −cos(nπ))
n
2
π
2
c
.
5. u(x, t) =
∞
n=1
a
n
cos
nπct
a
sin
nπx
a
, a
n
=2U
0
1 −cos(nπ/2)
nπ
.
7. a. sin
nπx
a
;b.sin
2n −1
2
πx
a
.

464 Answers to Odd-Numbered Exercises
9. Product solutions are φ
n
(x)T
n
(t),where
φ
n
(x) = sin(λ
n
x), T
n
(t) = exp
−kc
2
t/2
×
sin(µ
n
t)
cos(µ
n
t),
λ
n
=
nπ
a
,µ
n
=
λ
2
n
c
2
−
1
4
k
2
c
4
.
11. Product solutions are φ
n
(x)T
n
(t),where
φ
n
(x) = sin
nπx
a
,
T
n
(t) = sin or cos
n
2
π
2
ct
a
2
.
Frequencies n
2
π
2
c/a
2
.
13. The general solution of the differential equation is φ(x) = A cos(λx) +
B sin(λx) + C cosh(λx) + D sinh(λx). Boundary conditions at x = 0re-
quire A =−C, B =−D;thoseatx = a lead to C/D =−(cosh(λa) +
cos(λa))/(sinh(λa)− sin(λa)) and 1 + cos(λa) cosh(λa) = 0. The first
eigenvalues are λ
1
= 1.875/a, λ
2
= 4.693/a, and the eigenfunctions are
similar to the functions shown in the figure.
15. u(x, t) =
∞
n=1
a
n
cos(µ
n
t) +b
n
(sin µ
n
t)
sin(λ
n
x): λ
n
=nπ/a,
µ
n
=
λ
2
n
+γ
2
c, a
n
=2h
1 −cos(nπ)
/nπ,b
n
=0, n = 1, 2,....
17. Convergence is uniform because
|b
n
| converges.
Section 3.3
1. Table shows u(x, t)/h.
t
x 00.2a/c 0.4a/c 0.8a/c 1.4a/c
0.25a 0.5 0.5 0.2 −0.5 −0.2
0.5a 1.0 0.6 0.2 −0.6 −0.2
3. u(0, 0.5a/c) = 0; u(0.2a, 0.6a/c) = 0.2αa; u(0.5a, 1.2a/c) =−0.2αa.
(Hint: G(x) = αx,0< x < a.)
5. G(x) =
0, 0 < x < 0.4a,
5(x − 0.4a), 0.4a < x < 0.6a,
a, 0.6a < x < a.
Notice that G is a continuous function whose graph is composed of line
segments.
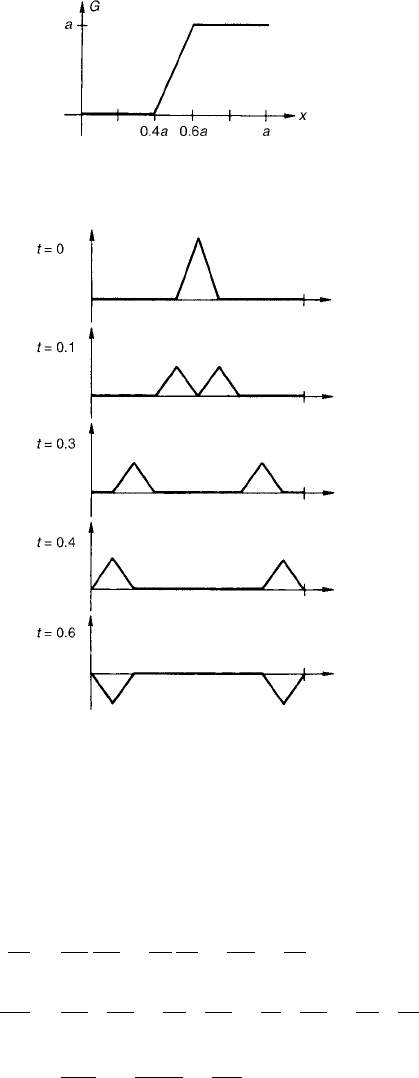
Chapter 3 465
Figure 2 Solution for Exercise 7, Section 3.3.
Figure 3 Solution for Exercise 9, Section 3.3.
7. See Fig. 2.
9. See Fig. 3.
11. By the chain rule we calculate
∂u
∂x
=
∂v
∂w
∂w
∂x
+
∂v
∂z
∂z
∂x
=
∂v
∂w
+
∂v
∂z
,
∂
2
u
∂x
2
=
∂
∂w
∂v
∂w
+
∂v
∂z
∂w
∂x
+
∂
∂z
∂v
∂w
+
∂v
∂z
∂z
∂x
=
∂
2
v
∂w
2
+2
∂
2
v
∂w∂z
+
∂
2
v
∂z
2

466 Answers to Odd-Numbered Exercises
and similarly
∂
2
u
∂t
2
=c
2
∂
2
v
∂w
2
−2
∂
2
v
∂z∂w
+
∂
2
v
∂z
2
.
(We have assumed that the two mixed partials ∂
2
v/∂z∂w and ∂
2
v/∂w∂z
are equal.) If u(x, t) satisfies the wave equation, then
∂
2
u
∂x
2
=
1
c
2
∂
2
u
∂t
2
.
In terms of the function v and the new independent variables this equa-
tion becomes
∂
2
v
∂w
2
+2
∂
2
v
∂z∂w
+
∂
2
v
∂z
2
=
∂
2
v
∂w
2
−2
∂
2
v
∂z∂w
+
∂
2
v
∂z
2
or, simply,
∂
2
v
∂z∂w
=0.
13. u(x, t) =−c
2
cos(t) + φ(x −ct) +ψ(x + ct).
Section 3.4
1. If f and g are sectionally smooth and f is continuous.
3. The frequency is cλ
n
rads/sec, and the period is 2π/cλ
n
sec.
5. Separation of variables leads to the following in place of Eqs. (11)
and (12):
T
+γ T
+λ
2
c
2
T = 0, (11
)
s(x)φ
−q(x)φ + λ
2
p(x)φ = 0. (12
)
The solutions of Eq. (11
) all approach 0 as t →∞,ifγ>0.
7. The period of T
n
(t) = a
n
cos(λ
n
ct) +b
n
sin(λ
n
ct) is 2π/λ
n
c.AllT
n
’s have
a common period p if and only if for each n there is an integer m such
that m(2π/λ
n
c) = p,orm = (pc/2π)λ
n
is an integer. For λ
n
as shown
and β = q/r,whereq and r are integers, this means
m =
pc
2π
α
n +
q
r
or
m =
pc
2π
α
r
(rn + q).
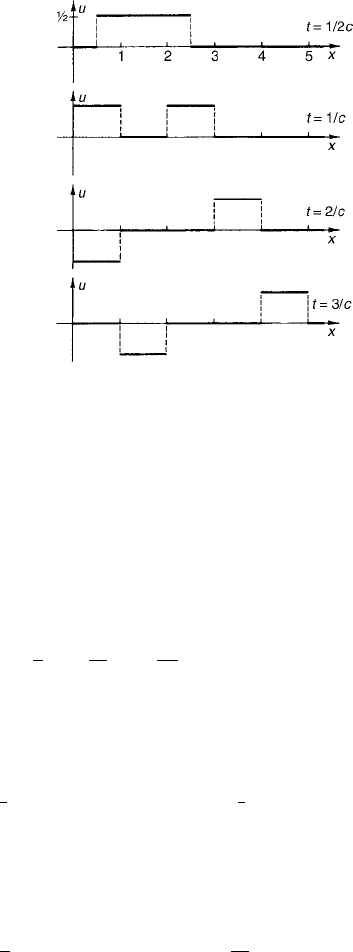
Chapter 3 467
Figure 4 Solution for Exercise 3, Section 3.6.
Given α, p can be adjusted so that m is an integer whenever n is an integer.
Section 3.5
1. If q ≥0, the numerator in Eq. (3) must also be greater than or equal to 0,
since φ
1
(x) cannot be identically 0.
3. 2π
2
/3isoneestimatefromy = sin(πx).
5.
2
1
(y
)
2
dx =
1
3
,
2
1
y
2
x
4
dx =
25
6
−6ln2;
N(y)/D(y) = 42.83; λ
1
≤6.54.
Section 3.6
1. u(x, t) =
1
2
[ f
e
(x +ct) +G
o
(x +ct)] +
1
2
[ f
e
(x −ct) −G
o
(x −ct)], where f
e
is the even extension of f and G
o
is the odd extension of G .
3. See Fig. 4.
5. See Fig. 5.
7. u(x, t) =
1
2
f (x +ct) + f (x − ct)
+
1
2c
x+ct
x−ct
g(y)dy.
Chapter 3 Miscellaneous Exercises
1. u(x, t) =
∞
1
b
n
sin(λ
n
x) cos(λ
n
ct), b
n
=2
1−cos(nπ)
/nπ, λ
n
=nπ/a.
