Powers D.L. Boundary Value Problems and Partial Differential Equations
Подождите немного. Документ загружается.

98 Chapter 1 Fourier Series and Integrals
The addition formula for sines gives the equality
sin
N +
1
2
y
=cos(Ny) sin
1
2
y
+sin(Ny) cos
1
2
y
.
Substituting it in Eq. (13) and using simple properties of integrals, we ob-
tain
S
N
(x) −f (x) =
1
π
π
−π
f (x +y) −f (x)
1
2
cos(Ny) dy
+
1
π
π
−π
f (x +y) −f (x)
cos(
1
2
y)
2sin(
1
2
y)
sin(Ny) dy. (14)
ThefirstintegralinEq.(14)canberecognizedastheFouriercosinecoeffi-
cient of the function
ψ(y) =
1
2
f (x +y) −f (x)
. (15)
Since f is a sectionally smooth function, so is ψ , and the first integral has
limit 0 as N increases, by Lemma 3.
The second integral in Eq. (14) can also be recognized, as the Fourier sine
coefficient of the function
φ(y) =
f (x +y) −f (x)
2sin(
1
2
y)
cos
1
2
y
. (16)
To proceed as before, we must show that φ(y) is at least sectionally contin-
uous, −π ≤ y ≤ π . The only difficulty is to show that the apparent division
by 0 at y =0doesnotcauseφ(y) to have a bad discontinuity there.
First, if f is continuous and differentiable near x,thenf (x + y) − f (x) is
continuous and differentiable near y = 0. Then L’Hôpital’s rule gives
lim
y→0
f (x +y) −f (x)
2sin(
1
2
y)
= lim
y→0
f
(x +y)
cos(
1
2
y)
=f
(x). (17)
Under these conditions, the function φ(y) of Eq. (16) has a removable dis-
continuity at y = 0 and thus is sectionally continuous.
Second, if f is continuous at x but has a corner there, then f (x +y) −f (x )
is continuous with a corner at y = 0. In this case, L’Hôpital’s rule applies
with the one-sided limits, which show
lim
y→0+
f (x +y) −f (x)
2sin(
1
2
y)
= lim
y→0+
f
(x + y)
cos(
1
2
y)
=f
(x+), (18)
lim
y→0−
f (x +y) −f (x)
2sin(
1
2
y)
= lim
y→0−
f
(x + y)
cos(
1
2
y)
=f
(x−). (19)
1.7 Proof of Convergence 99
Under these conditions, the function φ(y) of Eq. (16) has a jump disconti-
nuity at y = 0 and again is sectionally continuous.
In either case, we see that the second integral in Eq. (14) is the Fourier
sine coefficient of a sectionally continuous function. By Lemma 3, then, it
too has limit 0 as N increases, and the proof is complete for every x where
f is continuous.
Part 4. If f is not continuous at x.
Now let us suppose that f has a jump discontinuity at x.Inthiscase,we
must return to Part 2 and express the proposed sum of the series as
1
2
f (x +) +f (x−)
=
1
π
π
0
f (x +)
1
2
+
N
n=1
cos(ny)
dy
+
1
π
0
−π
f (x−)
1
2
+
N
n=1
cos(ny)
dy. (20)
Here, we have used the evenness of the integrand in Lemma 1 to write
1
π
π
0
1
2
+
N
n=1
cos(ny)
dy =
1
π
0
−π
1
2
+
N
n=1
cos(ny)
dy =
1
2
. (21)
Next, we have a convenient way to write the quantity to be limited:
S
N
(x) −
1
2
f (x +) +f (x−)
=
1
π
π
0
f (x +y) −f (x+)
1
2
+
N
n=1
cos(ny)
dy
+
1
π
0
−π
f (x +y) −f (x−)
1
2
+
N
n=1
cos(ny)
dy. (22)
The interval of integration for S
N
(x) asshowninEq.(10)hasbeensplitin
half to conform to the integrals in Eq. (20).
The last step is to show that each of the integrals in Eq. (22) approaches 0
as N increases. Since the technique is the same as in Part 3, this is left as an
exercise.
Let us emphasize that the crux of the proof is to show that the function
from Eq. (16),
φ(y) =
f (x +y) −f (x)
2sin(
1
2
y)
cos
1
2
y
(23)
(orasimilarfunctionthatarisesfromtheintegrandsinEq.(22)),doesnot
have a bad discontinuity at y =0.

100 Chapter 1 Fourier Series and Integrals
EXERCISES
1. Verify Lemma 2. Multiply through by 2 sin(
1
2
y). Use the identity
sin
1
2
y
cos(ny) =
1
2
sin
n +
1
2
y
−sin
n −
1
2
y
.
Note that most of the series then disappears. (To see this, write out the
result for N = 3.)
2. Verify Lemma 1 by integrating the sum term by term.
3. Let f (x) = f (x + 2π) and f (x) =|x| for −π<x <π.Notethatf is con-
tinuous and has a corner at x = 0. Sketch the function φ(y) as defined in
Eq. (16) if x = 0. Find φ(0+) and φ(0−).
4. Let f be the odd periodic extension of the function whose formula is π −x
for 0 < x <π.Inthiscase,f has a jump discontinuity at x = 0. Taking
x = 0, sketch the functions
φ
R
(y) =
f (x +y) −f (x+)
2sin(
1
2
y)
cos
1
2
y
(y > 0),
φ
L
(y) =
f (x +y) −f (x−)
2sin(
1
2
y)
cos
1
2
y
(y < 0).
(These functions appear if the integrands in Eq. (22) are developed as in
Part 3 of the proof.)
5. Consider the function f that is periodic with period 2π and has the formula
f (x) =|x|
3/4
for −π<x <π.
a. Show that f is continuous at x = 0 but is not sectionally smooth.
b. Show that the function φ(y) (from Eq. (16), with x = 0) is sectionally
continuous, −π<x <π, except for a bad discontinuity at y = 0.
c. Show that the Fourier coefficients of φ(y) tend to 0 as n increases, de-
spite the bad discontinuity.
1.8 Numerical Determination of Fourier Coefficients
There are many functions whose Fourier coefficients cannot be determined
analytically because the integrals involved are not known in terms of easily
evaluated functions. Also, it may happen that a function is not known explic-
itly but that its value can be found at some points. In either case, if a Fourier
1.8 Numerical Determination of Fourier Coefficients 101
series is to be found for the function, some numerical technique must be em-
ployed to approximate the integrals that give the Fourier coefficients. It turns
out that one of the crudest numerical integration techniques is the best.
Any periodic, sectionally smooth function can be reduced by the procedure
illustrated in Fig. 11 to the sum of some functions f
1
(x) and f
2
(x), whose series
can be found by integration, and another function that is continuous,periodic,
and sectionally smooth. This last function’s Fourier coefficients will approach
0 rapidly with n.
Suppose then that f (x) is continuous, sectionally smooth, and periodic with
period 2a. We wish to find its Fourier coefficients numerically. For instance,
a
0
=
1
2a
a
−a
f (x ) dx.
The integral is approximated using the trapezoidal rule. First, cut up the inter-
val −a < x < a into r equal subintervals with endpoints x
0
, x
1
,...,x
r
where
x
k
=−a +kx,x =
2a
r
.
Next, evaluate the sum
a
0
∼
=
1
2a
1
2
f (x
0
) +f (x
1
) +···+f (x
r−1
) +
1
2
f (x
r
)
x. (1)
Since x
0
=−a, x
r
=a,andf is periodic with period 2a,wehavef (x
0
) =f (x
r
):
The two terms with
1
2
multipliers can be combined. Thus, our approxima-
tion is
a
0
∼
=
1
2a
f (x
1
) +f (x
2
) +···+f (x
r
)
·
2a
r
.
The occurrences of 2a cancel, and the computed value is just the average of the
functional values.
We use a caret over the usual coefficient name to designate approximations.
Other Fourier coefficients are approximated in a similar way.
Summary
Let f (x) be continuous, sectionally smooth and periodic with period 2a.Ap-
proximate Fourier coefficients of f (x) are
ˆa
0
=
1
r
f (x
1
) +···+f (x
r
)
, (2)
ˆa
n
=
2
r
f (x
1
) cos
n πx
1
a
+···+f (x
r
) cos
n πx
r
a
, (3)
ˆ
b
n
=
2
r
f (x
1
) sin
n πx
1
a
+···+f (x
r
) sin
n πx
r
a
. (4)

102 Chapter 1 Fourier Series and Integrals
Figure 11 Preparation of a function for numerical integration of Fourier co-
efficients. (a) Graph of sectionally smooth function f (x) given on −a < x < a.
(b) Graph of f
1
(x), which has jumps of the same magnitude and position as f (x).
Coefficients can be found analytically. (c) Graph of f (x) −f
1
(x).Thisfunctionhas
no jumps in −a < x < a.(d)Graphoff
2
(x). The periodic extensions of f
2
(x) and
of f (x) −f
1
(x) have jumps of the same magnitude at x =±a, and so forth. The co-
efficients of f
2
can be found analytically. (e) Graph of f
3
(x) = f (x) − f
1
(x) − f
2
(x).
The Fourier series of f
3
(x) converges uniformly (the coefficients tend to zero
rapidly).

1.8 Numerical Determination of Fourier Coefficients 103
If r is odd, Eqs. (3) and (4) are valid for n = 1, 2,...,(r −1)/2, giving a total of
r coefficients. If r is even, Eq. (4) gives
ˆ
b
r/2
=0, and Eq. (3) has to be modified:
ˆa
r/2
=
1
r
f (x
1
) cos
r πx
1
2a
+···+f (x
r
) cos
r πx
r
2a
. (3
)
We again get r valid coefficients.
The formulas in Eqs. (2)–(4) were derived for the case in which x
0
, x
1
,...,x
r
are equally spaced points in the interval −a ≤ x ≤ a. However, they remain
valid for equally spaced points on the interval 0 ≤x ≤2a.Thatis,
x
0
=0, x
1
=
2a
r
, x
2
=
4a
r
, ..., x
r
=2a. (5)
Note also that when f (x) is given in the interval 0 ≤x ≤ a and the sine or co-
sine coefficients are to be determined, the formulas may be derived from those
already given here. Let the interval be divided into s equal subintervals with
endpoints 0 = x
0
, x
1
,...,x
s
= a (in general, x
i
= ia/s). Then the approximate
Fourier cosine coefficients for f or its even extension are
ˆa
0
=
1
s
1
2
f (x
0
) +f (x
1
) +···+f (x
s−1
) +
1
2
f (x
s
)
,
ˆa
n
=
2
s
1
2
f (x
0
) +f (x
1
) cos
n πx
1
a
+···+
1
2
f (x
s
) cos
n πx
s
a
,
n =1,...,s −1,
ˆa
s
=
1
s
1
2
f (x
0
) +f (x
1
) cos
s πx
1
a
+···+
1
2
f (x
s
) cos
s πx
s
a
. (6)
Similarly, the approximate Fourier sine coefficients for f or its odd extension
are
ˆ
b
n
=
2
s
f (x
1
) sin
n πx
1
a
+···+f (x
s−1
) sin
n πx
s−1
a
,
n =1, 2,...,s. (7)
An important feature of the approximate Fourier coefficients is this: If
F(x) =ˆa
0
+ˆa
1
cos
πx
a
+
ˆ
b
1
sin
πx
a
+···
is a finite Fourier series using a total of r approximate coefficients calculated
from Eqs. (3) and (4), then F(x) actually interpolates the function f (x) at
x
1
, x
2
,...,x
r
.Thatis,
F(x
i
) =f (x
i
), i =1, 2,...,r.

104 Chapter 1 Fourier Series and Integrals
ix
i
cos x
i
cos 2x
i
cos 3x
i
sin(x
i
)/x
i
00 1.01.01.01.0
1
π
6
0.86603 0.50 0.95493
2
π
3
0.5 −0.5 −1.00.82699
3
π
2
0 −1.00 0.63662
4
2π
3
−0.5 −0.51.00.41350
5
5π
6
−0.86603 0.50 0.19099
6 π −1.01.0 −1.00.0
Tab le 3 Numerical information
n ˆa
n
a
n
Error
00.58717 0.58949 0.00232
10.45611 0.45141 0.00470
2 −0.06130 −0.05640 0.00490
30.02884 0.02356 0.00528
Tab le 4 Approximate coefficients
of sin(x)/x
Thus the graph of F(x) cuts the graph of f (x) at the points x
i
, i = 1, 2,...,r.
Example.
Calculate the approximate Fourier coefficients of f (x) = sin(x)/x in −π<
x <π.Sincef is even, it will have a cosine series. We simplify computation by
using the half-range formulas and making s even. We take s = 6, x
0
= 0, x
1
=
π/6,...,x
5
=5π/6, x
6
=π. The numerical information is given in Table 3.
The results of the calculation are given in Table 4. On the left are the approx-
imate coefficients calculated from the table. On the right are the correct values
(to five decimals), obtained with the aid of a table of the sine integral (see Ex-
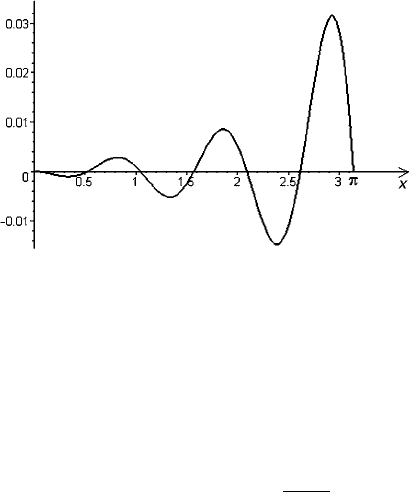
ercise 2). Figure 12 shows the difference between f (x) and F(x) (the sum of the
Fourier series using the approximate coefficients through ˆa
6
).
For hand calculation, choosing s to be a multiple of 4 makes many of the
cosines “easy” numbers such as 1 and 0.5. When the calculation is done by
digital computer, this is not a consideration.
EXERCISES
1. Since Table 3 gives sin(x)/x for seven points, seven cosine coefficients can
be calculated. Find ˆa
6
.
1.8 Numerical Determination of Fourier Coefficients 105
Figure 12 Graph of the difference between f (x) =sin(x)/x and F(x), the sum of
the Fourier series using the approximate coefficients ˆa
0
through ˆa
6
.
2.
Express the Fourier cosine coefficients of the example in terms of integrals
of the form
Si
(n +1)π
=
(n+1)π
0
sin(t)
t
dt.
This is the sine integral function and is tabulated in many books, especially
Handbook of Mathematical Functions, Abramowitz and Stegun, 1972.
3. Each entry in the list that follows represents the depth of the water in Lake
Ontario (minus the low-water datum of 242.8 feet) on the first of the cor-
responding month. Assuming that the water level is a periodic function
of period one year, and that the observations are taken at equal intervals,
compute the Fourier coefficients ˆa
0
, ˆa
1
,
ˆ
b
1
, ˆa
2
,
ˆ
b
2
, thus identifying the
mean level, and fluctuations of period 12 months, 6 months, 4 months,
and so forth. Take x
0
as January, ..., x
11
as December, and x
12
as January
again.
Jan. 0.75 July 2.35
Feb. 0.60 Aug. 2.15
Mar. 0.65 Sept. 1.75
Apr. 1.15 Oct. 1.05
May 1.80 Nov. 1.00
June 2.25 Dec. 0.90
4. The numbers in the table that follows represent the monthly precipi-
tation(ininchesofwater)inLakePlacid,NY,averagedoverthepe-
riod 1950–1959. Find the approximate Fourier coefficients ˆa
0
,...,ˆa
6
and
ˆ
b
1
,...,
ˆ
b
5
.

106 Chapter 1 Fourier Series and Integrals
Jan. 2.751 July 3.861
Feb. 2.004 Aug. 4.088
Mar. 3.166 Sept. 4.093
Apr. 2.909 Oct. 3.434
May 3.215 Nov. 2.902
June 3.767 Dec. 3.011
1.9 Fourier Integral
In Sections 1 and 2 of this chapter we developed the representation of a pe-
riodic function in terms of sines and cosines with the same period. Then, by
means of periodic extension, we obtained series representations for functions
defined only on a finite interval. Now we must deal with nonperiodic functions
defined for x between −∞ and ∞. Can such functions also be represented in
terms of sines and cosines? We make some transformations that suggest an
answer.
Suppose f (x) is defined for −∞ < x < ∞ and is sectionally smooth in every
finite interval. Then for any positive a, f (x) can be represented in the interval
−a < x < a by its Fourier series:
f (x) = a
0
+
∞
n=1
a
n
cos
n πx
a
+b
n
sin
n πx
a
, −a < x < a,
a
0
=
1
2a
a
−a
f (x) dx, a
n
=
1
a
a
−a
f (x ) cos
n πx
a
dx,
b
n
=
1
a
a
−a
f (x ) sin
n πx
a
dx. (1)
Example 1.
Let
f (x) =
e
−x
, 0 < x,
0, x < 0.
For any a > 0, we have the Fourier series for f (x) on the interval −a < x < a:
f (x) = a
0
+
∞
1
a
n
cos
n πx
a
+b
n
sin
n πx
a
, −a < x < a,
a
0
=
1 −e
−a
2a
, a
n
=
1 −e
−a
cos(n π)
a(1 +(n π/a)
2
)
,
b
n
=
(1 −e
−a
cos(nπ))nπ
a
2
(1 +(nπ/a)
2
)
. (2)
(The series converges to 1/2atx =0andtoe
−a
/2atx =a.)

1.9 Fourier Integral 107
Now we modify Eq. (1). Let λ
n
=nπ/a and define two functions
A
a
(λ) =
1
π
a
−a
f (x) cos(λx) dx, B
a
(λ) =
1
π
a
−a
f (x) sin(λx) dx. (3)
Notice that
a
n
=
π
a
A
a
(λ
n
), b
n
=
π
a
B
a
(λ
n
).
Because of this, the Fourier series Eq. (1) becomes
f (x ) = a
0
+
∞
n=1
A
a
(λ
n
) cos(λ
n
x) + B
a
(λ
n
) sin(λ
n
x)
·λ, −a < x < a, (4)
where λ = π/a =λ
n+1
−λ
n
.
The form in which Eq. (4) is written is chosen to suggest an integral with
respect to λ over the interval 0 <λ<∞. We may imagine a increasing to
infinity, so λ → 0and
A
a
(λ) → A(λ) =
1
π
∞
−∞
f (x) cos(λx) dx, (5)
B
a
(λ) →B(λ) =
1
π
∞
−∞
f (x) sin(λx) dx, (6)
and a
0
→0. Then Eq. (4) suggests
f (x ) =
∞
0
A(λ) cos(λx) +B(λ) sin(λx)
dλ, −∞ < x < ∞. (7)
Example 1 (continued).
For f (x) as in Example 1, we find
A(λ) =
1
π
∞
0
e
−x
cos(λx) dx =
1
π(1 +λ
2
)
,
B(λ) =
1
π
∞
0
e
−x
sin(λx) dx =
λ
π(1 +λ
2
)
,
and therefore we expect that
∞
0
1
π(1 +λ
2
)
cos(λx) +
λ
π(1 +λ
2
)
sin(λx)
dx =
e
−x
, 0 < x,
0, x < 0.
The foregoing derivation is not a proof, but it does suggest the following
theorem.
