Powers D.L. Boundary Value Problems and Partial Differential Equations
Подождите немного. Документ загружается.


118 Chapter 1 Fourier Series and Integrals
˙y(t) =
∞
n=1
−nA
n
sin(nt) +nB
n
cos(nt),
¨y(t) =
∞
n=1
−n
2
A
n
cos(nt) − n
2
B
n
sin(nt).
Then the differential equation can be written in the form
βA
0
+
∞
n=1
−n
2
A
n
+αnB
n
+βA
n
cos(nt)
+
∞
n=1
−n
2
B
n
−αnA
n
+βB
n
sin(nt) = a
0
+
∞
n=1
a
n
cos(nt) + b
n
sin(nt).
The A’s and B’s are now determined by matching coefficients
βA
0
= a
0
,
β −n
2
A
n
+αnB
n
= a
n
,
−αnA
n
+
β − n
2
B
n
= b
n
.
When these equations are solved for the A’s and B’s, we find
A
n
=
(β − n
2
)a
n
−αnb
n
, B
n
=
(β − n
2
)b
n
+αna
n
,
where
=
β −n
2
2
+α
2
n
2
.
Now, given the function f ,thea’s and b’s can be determined, thus giving the
A’s and B’s. The function y(t) represented by the series found is the periodic
part of the response. Depending on the initial conditions, there may also be a
transient response, which dies out as t increases.
Example.
Consider the differential equation
¨y +0.4˙y +1.04y = r(t).
If r(t) = sin(nt), the corresponding particular solution is
y(t) =
−0.4n cos(nt) +(1.04 −n
2
) sin(nt)
(1.04 −n
2
)
2
+(0.4n)
2
.

1.11 Applications of Fourier Series and Integrals 119
Next, suppose that r(t) is a square-wave function with Fourier series
r(t) =
∞
n=1
2(1 −cos(nπ))
nπ
sin(nt).
The corresponding response is
y(t) =
∞
n=1
2(1 −cos(nπ))
nπ
·
−0.4n cos(nt) +(1.04 −n
2
) sin(nt)
(1.04 −n
2
)
2
+(0.4n)
2
.
Note that the term for n = 1 has a small denominator, causing a large
response.
B. Boundary Value Problems
By way of introduction to the next chapter, we apply the idea of Fourier series
to the solution of the boundary value problem
d
2
u
dx
2
+pu = f (x), 0 < x < a,
u(0) =0, u(a) = 0.
First, we will assume that f (x) is equal to its Fourier sine series,
f (x) =
∞
n=1
b
n
sin
n πx
a
, 0 < x < a.
And second, we will assume that the solution u(x), which we are seeking,
equals its Fourier sine series,
u(x) =
∞
n=1
B
n
sin
n πx
a
, 0 < x < a,
and that this series may be differentiated twice to give
d
2
u
dx
2
=
∞
n=1
−
n
2
π
2
a
2
B
n
sin
n πx
a
, 0 < x < a.
When we insert the series forms for u, u
,andf (x) into the differential
equation, we find that
∞
n=1
−
n
2
π
2
a
2
B
n
+pB
n
sin
n πx
a
=
∞
n=1
b
n
sin
n πx
a
, 0 < x < a.
120 Chapter 1 Fourier Series and Integrals
Since the coefficients of like terms in the two series must match, we may con-
clude that
p −
n
2
π
2
a
2
B
n
=b
n
, n =1, 2, 3,....
If it should happen that p = m
2
π
2
/a
2
for some positive integer m,thereis
no value of B
m
that satisfies
p −
m
2
π
2
a
2
B
m
=b
m
unless b
m
= 0 also, in which case any value of B
m
is satisfactory. In summary,
we may say that
B
n
=
b
n
p −n
2
π
2
/a
2
and
u(x) =
∞
n=1
a
2
b
n
a
2
p −n
2
π
2
sin
n πx
a
,
with the agreement that a zero denominator must be handled separately.
Example.
Consider the boundary value problem
d
2
u
dx
2
−u =−x, 0 < x < 1,
u(0) = 0, u(1) = 0.
We have found previously that
−x =
∞
n=1
2(−1)
n
πn
sin(n πx), 0 < x < 1.
Thus, by the preceding development, the solution must be
u(x) =
∞
n=1
2
π
(−1)
n+1
n(n
2
π
2
+1)
sin(n πx), 0 < x < 1.
Although this particular series belongs to a known function, one would not,
in general, know any formula for the solution u(x) other than its Fourier sine
series.
1.11 Applications of Fourier Series and Integrals 121
C. The Sampling Theorem
One of the most important results of information theory is the sampling the-
orem, which is based on a combination of the Fourier series and the Fourier
integral in their complex forms. What the electrical engineer calls a signal is
just a function f (t) defined for all t. If the function is integrable, there is a
Fourier integral representation for it:
f (t) =
∞
−∞
C(ω) exp(iωt) dω,
C(ω) =
1
2π
∞
−∞
f (t) exp(−iωt) dt.
Asignaliscalledband limited if its Fourier transform is zero except in a
finite interval, that is, if
C(ω) = 0, for |ω| >.
Then is called the cutoff frequency. If f is band limited, we can write it in
the form
f (t) =
−
C(ω) exp(iωt) dω (1)
because C(ω) is zero outside the interval −<ω<.Wefocusourattention
on this interval by writing C(ω) as a Fourier series:
C(ω) =
∞
−∞
c
n
exp
in πω
, −<ω<. (2)
The (complex) coefficients are
c
n
=
1
2
−
C(ω) exp
−in πω
dω.
The point of the sampling theorem is to observe that the integral for c
n
ac-
tually is a value of f (t) at a particular time. In fact, from the integral Eq. (1),
we see that
c
n
=
1
2
f
−nπ
.
Thus there is an easy way of finding the Fourier transform of a band-limited
function. We have
C(ω) =
1
2
∞
−∞
f
−nπ
exp
in πω

122 Chapter 1 Fourier Series and Integrals
=
1
2
∞
−∞
f
nπ
exp
−in πω
, −<ω<.
By utilizing Eq. (1) again, we can reconstruct f (t):
f (t) =
−
C(ω) exp(iωt) dω
=
1
2
∞
−∞
f
nπ
−
exp
−in πω
exp(iωt) dω.
Carrying out the integration and using the identity
sin(θ) =
(e
iθ
−e
−iθ
)
2i
,
we find
f (t) =
∞
−∞
f
nπ
sin(t −nπ)
t −nπ
. (3)
This is the main result of the sampling theorem. It says that the band-limited
function f (t) may be reconstructed from the samples of f at t = 0, ±π/,....
It is difficult to determine what functions are actually band limited. However,
the process usually works quite well.
In practice, we must use a finite series to approximate the function
f (t)
∼
=
N
−N
f
nπ
sin(t −nπ)
t −nπ
. (4)
Since the sampled values all come from the interval −Nπ/ to Nπ/,the
series cannot attempt to approximate the function outside that interval. An
animation on the CD shows the effects of choosing N and .
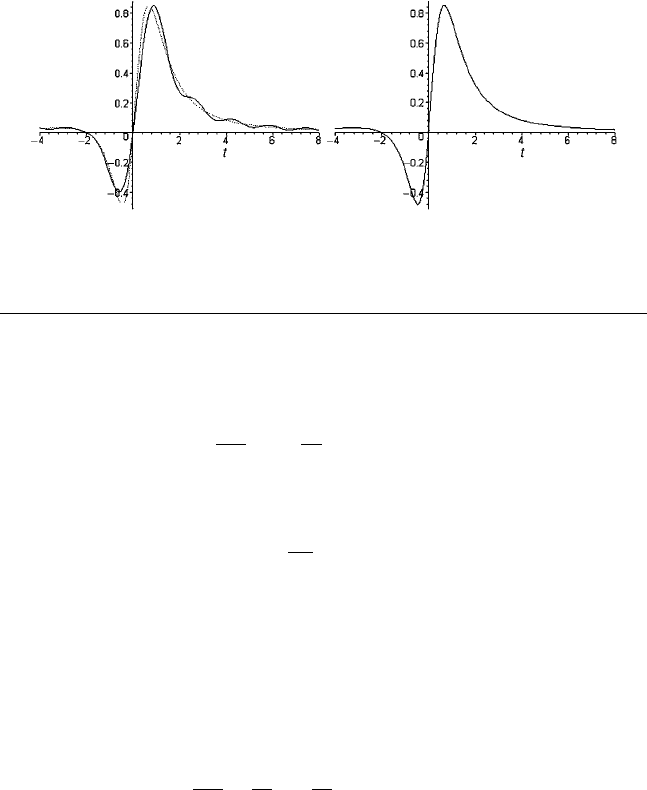
Example.
The function
f (t) =
t
2
+2t
(1 +t
2
)
2
is not band limited but can be approximated satisfactorily from a finite por-
tion of the sum as in Eq. (4). Figure 13 shows results for N = 100 (that
is, 201 terms) and = 4 and 10. The target function is dashed. Notice the
improvement.
1.11 Applications of Fourier Series and Integrals 123
Figure 13 Graphs of approximation using sampling: Eq. (4) with N = 100 and
= 4 and 10.
EXERCISES
1. Use the method of Part A to find a particular solution of
d
2
u
dt
2
+0.4
du
dt
+1.04u = r(t),
where r(t) is periodic with period 4π and
r(t) =
t
4π
, 0 < t < 4π.
2. In the solution of Exercise 1, calculate the magnitude of the coefficients of
the Fourier series of u(t) (periodic part).
3. A simply supported beam of length L has a point load w in the middle and
axial tension T. (See Exercises in Section 0.3.) Its displacement u(x) satisfies
the boundary value problem
d
2
u
dx
2
−
T
EI
u =
w
EI
h(x), 0 < x < L,
u(0) =0, u(L) = 0,
where h(x) is the “triangle function”
h(x) =
2x/L, 0 < x < L/2,
2(L −x)/L, L/2 < x < L.
Use the method of Part B to find u(x) as a sine series.
4. The inhomogeneity in the differential equation in Exercise 3 has a dis-
continuous derivative. Find another way to solve the differential equation.
Hint: Both u(x) and u
(x) must be continuous for 0 < x < L.

124 Chapter 1 Fourier Series and Integrals
5.
Usethesoftwaretoapproximatethefunctionf (t) = e
−t
2
by the Sampling
Theorem. Try =4, N =2.
6. Simplify the final formula for sampling to
f (t) =sin(t)
∞
−∞
f
nπ
(−1)
n
t −nπ
.
1.12 Comments and References
The first use of trigonometric series occurred in the middle of the eighteenth
century. Euler seems to have originated the use of orthogonality for the de-
termination of coefficients. In the early nineteenth century Fourier made ex-
tensive use of trigonometric series in studying problems of heat conduction
(see Chapter 2). His claim, that an arbitrary function could be represented as
a trigonometric series, led to an extensive reexamination of the foundations
of calculus. Fourier seems to have been among the first to recognize that a
function might have different analytical expressions in different places.
Dirichlet established sufficient conditions (similar to those of our conver-
gence theorem) for the convergence of Fourier series around 1830. Later, Rie-
mann was led to redefine the integral as part of his attempt to discover condi-
tions on a function necessary and sufficient for the convergence of its Fourier
series. This problem has never been solved. Many other great mathematicians
have founded important theories (the theory of sets, for one) in the course of
studying Fourier series, and they continue to be a subject of active research. An
entertaining and readable account of the history and uses of Fourier series is
in The Mathematical Ex perience, by Davis and Hersh. (See the Bibliography.)
Historical interest aside, Fourier series and integrals are extremely impor-
tant in applied mathematics, physics, and engineering, and they merit further
study. A superbly written and organized book is Tolstov’s Fourier Series.Its
mathematical prerequisites are not too high. Fourier Series and Boundary Value
Problems by Churchill and Brown is a standard text for some engineering ap-
plications.
About 1960 it became clear that the numerical computation of Fourier co-
efficients could be rearranged to achieve dramatic reductions in the amount
of arithmetic required. The result, called the fast Fourier transfor m ,orFFT,has
revolutionized the use of Fourier series in applications. See The Fast Fourier
Transform by James S. Walker.
The sampling theorem mentioned in the last section has become bread and
butter in communications engineering. For extensive information on this as
well as the FFT, see Integral and Discrete Transforms with Applications and Error
Analysis, by A.J. Jerri.

Miscellaneous Exercises 125
Chapter Review
See the CD for review questions.
Miscellaneous Exercises
1. Find the Fourier sine series of the trapezoidal function given for
0 < x <π by
f (x ) =
x/α, 0 < x <α,
1,α<x <π− α,
(π −x)/α, π −α<x <π.
2. Show that the series found in Exercise 1 converges uniformly.
3. When α approaches 0, the function of Exercise 1 approaches a square
wave. Do the sine coefficients found in Exercise 1 approach those of a
square wave?
4. Find the Fourier cosine series of the function
F(x) =
x
0
f (t) dt,
where f denotes the function in Exercise 1. Sketch.
5. Find the Fourier sine series of the function given in the interval 0 < x < a
by the formula (α is a parameter between 0 and 1)
f (x ) =
hx
αa
, 0 < x <αa,
h(a −x)
(1 −α)a
,αa < x < a.
6. Sketch the function of Exercise 5. To what does its Fourier sine series
converge at x = 0? at x = αa?atx = a?
7. Suppose that f (x) = 1, 0 < x < a. Sketch and find the Fourier series of
the following extensions of f (x):
a. even extension;
b. odd extension;
c. periodic extension (period a);
d. even periodic extension;

126 Chapter 1 Fourier Series and Integrals
e. odd periodic extension;
f. the one corresponding to f (x) = x, −a < x < 0.
8. Perform the same task as in Exercise 7, but f (x) = 0, 0 < x < a.
9. Find the Fourier series of the function given by
f (x) =
0, −a < x < 0,
2x, 0 < x < a.
Sketch the graph of f (x) and its periodic extension. To what values does
the series converge at x =−a, x =−a/2, x = 0, x = a,andx = 2a?
10. Sketch the odd periodic extension and find the Fourier sine series of the
function given by
f (x ) =
1, 0 < x <
π
2
,
1
2
,
π
2
< x <π.
To what values does the series converge at x = 0, x = π/2, x = π , x =
3π/2, and x = 2π ?
11. Sketch the even periodic extension of the function given in Exercise 10.
Find its Fourier cosine series. To what values does the series converge at
x = 0, x = π/2, x = π , x =3π/2, and x = 2π ?
12. Find the Fourier cosine series of the function
g(x) =
1 −x, 0 < x < 1,
0, 1 < x < 2.
Sketch the graph of the sum of the cosine series.
13. Find the Fourier sine series of the function defined by f (x) = 1 − 2x,
0 < x < 1. Sketch the graph of the odd periodic extension of f (x),and
determine the sum of the sine series at points where the graph has a
jump.
14. Following the same requirements as in Exercise 13, use the cosine series
and the even periodic extension.
15. Find the Fourier series of the function given by
f (x) =
0, −π<x < −
π
2
,
sin(2x), −
π
2
< x <
π
2
,
0,
π
2
< x <π.
Sketch the graph of the function.

Miscellaneous Exercises 127
16. Show that the function given by the formula f (x) = (π −x)/2, 0 < x <
2π, has the Fourier series
f (x ) =
∞
1
sin(nx)
n
, 0 < x < 2π.
Sketch f (x) and its periodic extension.
17. Use complex methods and a finite geometric series to show that
N
n=1
cos(nx) =
sin
(N +
1
2
)x
−sin(
1
2
x)
2sin(
1
2
x)
.
Then use trigonometric identities to identify
N
n=1
cos(nx) =
sin(
1
2
Nx) cos
1
2
(N + 1)x
sin(
1
2
x)
.
18. Identify the partial sums of the Fourier series in Exercise 16 as
S
N
(x) =
N
n=1
sin(nx)
n
.
The series of Exercise 17 is S
N
(x). Use this information to locate the max-
ima and minima of S
N
(x) in the interval 0 ≤ x ≤ π.Findthevalueof
S
N
(x) at the first point in the interval 0 < x <π where S
N
(x) = 0 for
N =5. Compare to (π −x)/2atthatpoint.
19. Find the Fourier sine series of the function given by
f (x ) =
sin
πx
a
, 0 < x < a,
0, a < x <π,
assuming that 0 < a <π.
20. Find the Fourier cosine series of the function given in Exercise 19.
21. Find the Fourier integral representation of the function given by
f (x ) =
1, 0 < x < a,
0, x < 0orx > a.
