Powers D.L. Boundary Value Problems and Partial Differential Equations
Подождите немного. Документ загружается.


68 Chapter 1 Fourier Series and Integrals
Let h(x) be an odd function defined in a symmetric interval −a < x < a. Then
a
−a
h(x) dx = 0.
Suppose now that g is an even function in the interval −a < x < a. Since the
sine function is odd and the product g(x) sin(nπx/a) is odd,
b
n
=
1
a
a
−a
g(x) sin
nπx
a
dx = 0.
That is, all the sine coefficients are zero. Also, since the cosine is even, so is
g(x) cos(nπ x/a),andthen
a
n
=
1
a
a
−a
g(x) cos
nπx
a
dx =
2
a
a
0
g(x) cos
nπx
a
dx.
Thus the cosine coefficients can be computed from an integral over the interval
from 0 to a.
Parallel results hold for odd functions: the cosine coefficients are all zero
and the sine coefficients can be simplified. We summarize the results.
Theorem 2. If g(x) is even on the interval −a < x < a (g(−x ) = g(x)),then
g(x) ∼ a
0
+
∞
n=1
a
n
cos
nπx
a
, −a < x < a,
where
a
0
=
1
a
a
0
g(x) dx, a
n
=
2
a
a
0
g(x) cos
nπx
a
dx.
If h(x) is odd on the interval −a < x < a (h(−x) =−h(x)),then
h(x) ∼
∞
n=1
b
n
sin
nπx
a
, −a < x < a,
where
b
n
=
2
a
a
0
h(x) sin
nπx
a
dx.
Very frequently, a function given in an interval 0 < x < a must be repre-
sented in the form of a Fourier series. There are infinitely many ways of do-
ing this, but two ways are especially simple and useful: extending the given
function to one defined on a symmetric interval −a < x < a by making the
extended function either odd or even.

1.2 Arbitrary Period and Half-Range Expansions 69
(a) (b)
(c) (d)
Figure 4 A function is given in the interval 0 < x < a (heavy curve). The figure
shows: (a) the odd extension; (b) the even extension; (c) the odd periodic exten-
sion; and (d) the even periodic extension.
Definition
Let f (x) be given for 0 < x < a.Theodd extension of f is defined by
f
o
(x) =
f (x), 0 < x < a,
−f (−x), −a < x < 0.
The even extension of f is defined by
f
e
(x) =
f (x), 0 < x < a,
f (−x), −a < x < 0.
Notice that if −a < x < 0, then 0 < −x < a, so the functional values on the
right are known from the given functions.
Graphically, the even extension is made by reflecting the graph in the vertical
axis. The odd extension is made by reflecting first in the vertical axis and then
in the horizontal axis (see Fig. 4).
Now the Fourier series of either extension may be calculated from the for-
mulas in Theorem 2. Since f
e
is even and f
o
is odd, we have
f
e
(x) ∼ a
0
+
∞
n=1
a
n
cos
nπx
a
, −a < x < a,
f
o
(x) ∼
∞
n=1
b
n
sin
nπx
a
, −a < x < a.

70 Chapter 1 Fourier Series and Integrals
If the series on the right converge, they actually represent periodic functions
with period 2a. The cosine series would represent the even periodic extension
of f — the periodic extension of f
e
; and the sine series would represent the odd
periodic extension of f .
When the problem at hand is to represent the function f (x) in the interval
0 < x < a, where it was originally given, we may use either the Fourier sine
series or the cosine series because both f
e
and f
o
coincide with f in the interval.
Thus we may summarize by saying: If f (x) is given for 0 < x < a,then
f (x) ∼ a
0
+
∞
n=1
a
n
cos
nπx
a
, 0 < x < a,
a
0
=
1
a
a
0
f (x ) dx, a
n
=
2
a
a
0
f (x ) cos
nπx
a
dx
and
f (x) ∼
∞
n=1
b
n
sin
nπx
a
, 0 < x < a,
b
n
=
2
a
a
0
f (x) sin
nπx
a
dx.
These two representations are called half-range expansions, and the series are
called the Fourier cosine and Fourier sine series of f ,respectively.Weshall
need these, more than any other kind of Fourier series, in the applications we
make later in this book.
Example.
Let us suppose that the function f has the formula
f (x ) = x, 0 < x < 1.
Then the odd periodic extension of f is as shown in Fig. 5, and the Fourier sine
coefficients of f are
b
n
=2
1
0
x sin(nπx ) dx =−
2
nπ
cos(nπ).
The even periodic extension of f is shown in Fig. 6. The Fourier cosine co-
efficients are
a
0
=
1
0
xdx=
1
2
,
a
n
= 2
1
0
x cos(nπx) dx =−
2
n
2
π
2
1 −cos(nπ)
.

1.2 Arbitrary Period and Half-Range Expansions 71
Figure 5 Odd periodic extension (period 2) of f (x) = x,0< x < 1.
Figure 6 Even periodic extension (period 2) of f (x ) = x,0< x < 1.
The following six correspondences (we will later show them to be equalities)
follow from the ideas of this section. Note that the inequalities showing the
applicable range of x are crucial.
∞
n=1
−2cos(nπ)
nπ
sin(nπx) ∼
f (x) = x, 0 < x < 1,
f
o
(x) = x, −1 < x < 1,
¯
f
o
(x), −∞< x < ∞,
1
2
−
∞
n=1
2(1 −cos(nπ))
n
2
π
2
cos(nπx) ∼
f (x) = x, 0 < x < 1,
f
e
(x) =|x|, −1 < x < 1,
¯
f
e
(x), −∞< x < ∞.
EXERCISES
1. Find the Fourier series of each of the following functions. Sketch the graph
of the periodic extension of f for at least two periods.
a. f (x) =|x|, −1 < x < 1;
b. f (x) =
−1, −2 < x < 0,
1, 0 < x < 2;
c. f (x) = x
2
, −
1
2
< x <
1
2
.

72 Chapter 1 Fourier Series and Integrals
2.
Show that the functions cos(nπx/a) and sin(nπx/a) satisfy orthogonality
relations similar to those given in Section 1.
3. Suppose a Fourier series is needed for a function defined in the interval
0 < x < 2a. Show how to construct a periodic extension with period 2a,
and give formulas for the Fourier coefficients that use only integrals from
0to2a. (Hint: See Exercise 5, Section 1.)
4. Show that the formula
e
x
=cosh(x) +sinh(x)
gives the decomposition of the function e
x
into a sum of an even and an
odd function.
5. Identify each of the following as being even, odd, or neither. Sketch on a
symmetric interval.
a. f (x) = x;
c. f (x) =|cos(x)|;
e. f (x) = x cos(x );
b. f (x) =|x|;
d. f (x) = arc sin(x);
f. f (x) = x +cos(x+1).
6. If f (x) isgivenintheinterval0< x < a, what other ways are there to
extend it to a function on −a < x < a?
7. Find the Fourier series of these functions.
a. f (x) = x, −1 < x < 1;
b. f (x) = 1, −2 < x < 2;
c. f (x) =
x, −
1
2
< x <
1
2
,
1 −x,
1
2
< x <
3
2
.
8. Is it true that if all the sine coefficients of a function f defined on −a
< x < a are zero, then f is even?
9. We know that if f (x) is odd on the interval −a < x < a, its Fourier se-
ries is composed only of sines. What additional symmetry condition on f
will make the sine coefficients with even indices be zero? Give an exam-
ple.
10. Sketch both the even and odd extensions of these functions.
a. f (x) = 1, 0 < x < a;
c. f (x) = sin(x),0< x < 1;
b. f (x) = x,0< x < a;
d. f (x) = sin(x),0< x <π.
11. Find the Fourier sine series and cosine series for the functions given in
Exercise 10. Sketch the even and odd periodic extensions for several peri-
ods.

1.3 Convergence of Fourier Series 73
12. Prove the orthogonality relations
a
0
sin
nπx
a
sin
mπx
a
dx =
0, n =m,
a/2, n = m,
a
0
cos
mπx
a
cos
nπx
a
dx =
0, n =m,
a/2, n = m = 0,
a, n = m = 0.
13. If f (x) is continuous on the interval 0 < x < a, is its even periodic ex-
tension continuous? What about the odd periodic extension? Check espe-
cially at x =0and±a.
14. Justify Theorem 1 by considering the integral as a sum of signed areas. See
Fig. 4 for typical even and odd functions.
15. Justify or prove these statements.
a. If h(x) is an odd function, then |h(x)| is an even function.
b. If f (x) is defined for all positive x,thenf (|x|) is an even func-
tion.
c. If f (x) is defined for all x and g(x) is any even function, then f (g(x)) is
even.
d. If h(x) is an odd function, g(x) is even, and g(x) is defined for all x,
then g(h(x)) is an even function.
1.3 Convergence of Fourier Series
Now we are ready to take up the second question of Section 1: Does the Fourier
series of a function actually represent that function? The word represent has
many interpretations, but for most practical purposes we really want to know
the answer to this question: If a value of x is chosen, the numbers cos(nπx/a)
and sin(nπx/a) are computed for each n and inserted into the Fourier series
of f , and the sum of the series is calculated, is that sum equal to the functional
value f (x)?
In this section we shall state, without proof, some theorems that answer the
question (a proof of the convergence theorem is given in Section 7). But first
we need a few definitions about limits and continuity.
The ordinary limit lim
x→x
0
f (x) can be rewritten as lim
h→0
f (x
0
+ h).Here
h may approach zero in any manner. But if h is required to be positive only, we
getwhatiscalledtheright-hand limit of f at x
0
,definedby
f (x
0
+) = lim
h→0+
f (x
0
+h) = lim
h→0
h>0
f (x
0
+h).
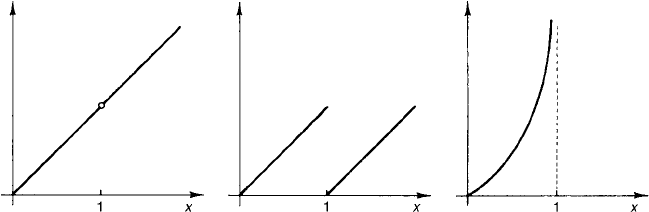
74 Chapter 1 Fourier Series and Integrals
(a) (b) (c)
Figure 7 Three functions with different kinds of discontinuities at x = 1.
(a) f (x ) = (x − x
2
)/(1 − x) has a removable discontinuity. (b) f (x) = x for
0 < x < 1andf (x) = x − 1for1< x; this function has a jump discontinuity.
(c) f (x) =−ln(|1 −x|) has a “bad” discontinuity.
The left-hand limit is defined similarly:
f (x
0
−) = lim
h→0−
f (x
0
+h) = lim
h→0
h<0
f (x
0
+h) = lim
h→0+
f (x
0
−h).
Note that f (x
0
+) and f (x
0
−) need not be values of the function f .
If both left- and right-hand limits exist and are equal, the ordinary limit
exists and is equal to the one-handed limits. It is quite possible that the left-
and right-handed limits exist but are different. This happens, for instance, at
x = 0 for the function
f (x) =
1, 0 < x <π,
−1, −π<x < 0.
In this case, the left-hand limit at x
0
= 0is−1, whereas the right-hand limit
is +1. A discontinuity at which the one-handed limits exist but do not agree is
called a jump discontinuity.
It is also possible that at some point both limits exist and agree but that the
function is not defined at that point or its value is not equal to the limit. In
suchacase,afunctionissaidtohavearemovable discontinuity.Ifthevalueof
the function at the troublesome point is redefined to be equal to the limit, the
function will become continuous. For example, the function f (x) = sin(x)/x
has a removable discontinuity at x = 0. The discontinuity is eliminated by re-
defining f (x) = sin(x)/x (x = 0), f (0) = 1. Removable discontinuities are so
simple that we may assume they have been removed from any function under
discussion.
Other discontinuities are more serious. They occur if one or both of the
one-handed limits fail to exist. Each of the functions sin(1/x), e
1/x
,1/x has a
discontinuity at x = 0thatisneitherremovablenorajump(seeFig.7).Table2
summarizes continuity behavior at a point.
1.3 Convergence of Fourier Series 75
Name Criterion
Continuity f (x
0
+) = f (x
0
−) = f (x
0
)
Removable discontinuity f (x
0
+) = f (x
0
−) = f (x
0
)
Jump discontinuity f (x
0
+) = f (x
0
−)
“Bad” discontinuity f (x
0
+) or f (x
0
−) or both fail to exist
Tab le 2 Types of continuity behavior at x
0
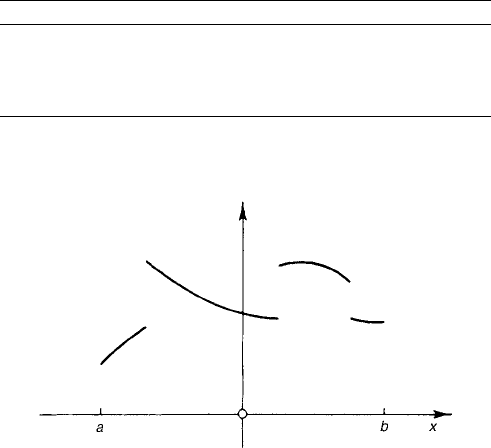
Figure 8 Typical sectionally continuous function made up of four continuous
“sections.”
We shall say that a function is sectionally continuous (also called piecewise
continuous)onanintervala < x < b if it is bounded and continuous, ex-
cept possibly for a finite number of jumps and removable discontinuities. (See
Fig. 8.) A function is sectionally continuous (without qualification) if it is sec-
tionally continuous on every interval of finite length. For instance, if a periodic
function is sectionally continuous on any interval whose length is one period
or more, then it is sectionally continuous.
Examples.
1. The square wave,definedby
f (x) =
1, 0 < x < a,
−1, −a < x < 0,
f (x +2a) = f (x),
is sectionally continuous. There are jump discontinuities at x = 0, ±a,
±2a,etc.
2. The function f (x) = 1/x cannot be sectionally continuous on any interval
that contains 0 or even has 0 as an endpoint, because the function is not
bounded at x = 0.
3. If f (x) = x, −1 < x < 1, then f is continuous on that interval. Its periodic
extension (see Fig. 3) is sectionally continuous but not continuous.

76 Chapter 1 Fourier Series and Integrals
The examples clarify a couple of facts about the meaning of sectional con-
tinuity. Most important is that a sectionally continuous function must not
“blow up” at any point — even an endpoint — of an interval. Note also that a
function need not be defined at every point in order to qualify as sectionally
continuous. No value was given for the square-wave function at x = 0, ±a,
but the function remains sectionally continuous, no matter what values are
assigned for these points.
Afunctionissectionally smooth (also, piecewise smooth)inanintervala <
x < b if: f is sectionally continuous; f
(x) exists, except perhaps at a finite
number of points; and f
(x) is sectionally continuous. The graph of a section-
ally smooth function then has a finite number of removable discontinuities,
jumps, and corners. (The derivative will not exist at these points.) Between
these points, the graph will be continuous, with a continuous derivative. No
vertical tangents are allowed, for these indicate that the derivative is infinite.
Examples.
1. f (x) =|x|
1/2
is continuous but not sectionally smooth in any interval that
contains 0, because |f
(x)|→∞as x →0.
2. Thesquarewaveissectionallysmoothbutnotcontinuous.
Most of the functions useful in mathematical modeling are sectionally
smooth. Fortunately we can also give a positive statement about the Fourier
series of such functions.
Theorem. If f (x) is sectionally smooth and periodic with period 2a, then at each
point x the Fourier series corresponding to f converges, and its sum is
a
0
+
∞
n=1
a
n
cos
nπx
a
+b
n
sin
nπx
a
=
f (x +) +f (x−)
2
.
See an animated example on the CD.
This theorem gives an answer to the question at the beginning of the section.
Recall that a sectionally smooth function has only a finite number of jumps
and no bad discontinuities in every finite interval. Hence,
f (x−) = f (x+) =
1
2
f (x +) +f (x−)
=f (x ),
exceptperhapsatafinitenumberofpointsonanyfiniteinterval.Forthisrea-
son, if f satisfies the hypotheses of the theorem, we write fequalto its Fourier
series, even though the equality may fail at jumps.
In constructing the periodic extension of a function, we never defined the
values of f (x) at the endpoints. Since the Fourier coefficients are given by in-
tegrals, the value assigned to f (x) at one point cannot influence them; in that

1.3 Convergence of Fourier Series 77
sense, the value of f at x =+a is unimportant. But because of the averaging
features of the Fourier series, it is reasonable to define
f (a) = f (−a) =
1
2
f (a−) + f (−a+)
.
That is, the value of f at the endpoints is the average of the one-handed limits
at the endpoints, each limit taken from the interior. For instance, if f (x) =
1 + x,0< x < 1, and f (x) = 0, −1 < x < 0, then f (±1) should be taken to
be 1, and f (0) should be
1
2
.
Examples.
1. The square-wave function
f (x) =
1, 0 < x < 1,
−1, −1 < x < 0
is sectionally smooth; therefore the corresponding Fourier series con-
verges to
1, for 0 < x < 1,
−1, for −1 < x < 0,
0, for x =0, 1, −1
and is periodic with period 2.
2. For the function f (x) =|x|
1/2
, −π<x <π, f (x + 2π) = f (x),thepre-
ceding theorem does not guarantee convergence of the Fourier series at
any point, even though the function is continuous. Nevertheless, the se-
ries does converge at any point x! This shows that the conditions in the
theorem are perhaps too strong. (But they are useful.)
EXERCISES
1. Foreachfunctiongiven,ifitisnotsectionallysmoothontheinterval,ex-
plain why not. Sketch.
a. f (x) =|x|−|1 −x|, −1 < x < 2;
b. f (x) =
√
|x|, −1 < x < 1;
c. f (x) = ln
2cos(x/2)
, −π<x <π;
d. f (x) = tan(x), 0 < x <π/2;
e. f (x) = tan(x), 0 < x <π.
2. Check each function described in what follows to see whether it is section-
ally smooth. If it is, state the value to which its Fourier series converges at
each point x in the interval and at the endpoints. Sketch.
